离散傅里叶变换（DFT）

最新推荐文章于 2024-06-14 11:47:18 发布

生信小兔

最新推荐文章于 2024-06-14 11:47:18 发布

阅读量2w

点赞数 8

分类专栏：机器学习基础数学基础文章标签：算法 python 傅里叶分析

本文链接：https://blog.csdn.net/weixin_60737527/article/details/126136965

版权

机器学习基础同时被 2 个专栏收录

20 篇文章 154 订阅

订阅专栏

数学基础

14 篇文章 37 订阅

订阅专栏

离散傅里叶变换(Discrete Fourier Transform)是信号分析中的一种基本方法，将离散时序信号从时间域变换到频率域，是傅里叶变换在时域和频域都呈离散的形式。

（1）基础知识

对于傅氏变换，其定义为：

$F(\omega)=\int_{-\infty }^{+\infty}f(t)e^{-i\omega t}dt$

利用该公式，可以实现对一些符合条件的连续函数进行傅氏变换。然而，在很多时候，我们所获得的时序信号并不是连续的，而是离散的序列，如下图所示。

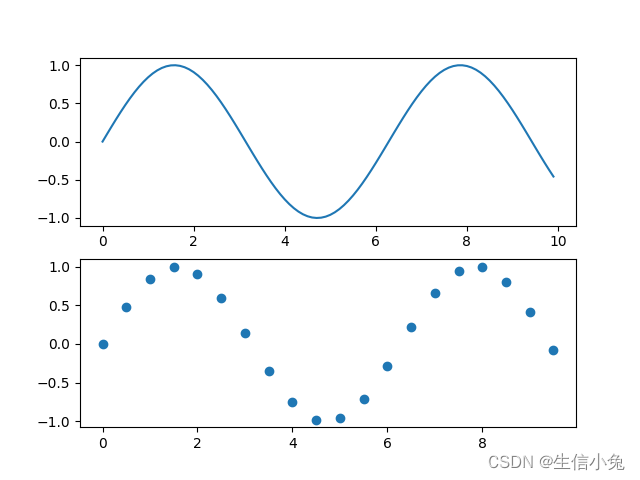
对于离散的序列，它的长度是有限的，并且由于不连续，故无法积分计算。若用梯形面积求和近似替代积分，又会出现无法进行无穷积分的情况。

（2）初步实现方法

针对上述问题，我们可以初步采用以下方法：将该序列进行重复平移，形成周期序列，并用求梯形面积的方法近似替代求积分。

利用欧拉公式对式子进行变换，计算正弦傅氏变换与余弦傅氏变换，分别得到正弦频域图与余弦频域图，频域信号由勾股定理对正余弦信号进行计算即可。

def dft1(s,t,repet,omega):
    '''s:时域离散信号
    t:对应时间
    reprt:计算傅里叶变换时信号向前与向后重复次数
    omega:频域信号频率范围与间隔'''
    dt=t[1]-t[0] #信号采样时间间隔
    n=len(t)
    l=t[-1]-t[0] #信号长度
    T=[]
    T.extend(t)
    S=[]
    for i in range(repet[0]+repet[1]+1):
        S.extend(s)
    for i in range(repet[1]):
        T.extend(np.array(t)+(i+1)*l)
    for i in range(repet[0]):
        for j in range(n):
            T.insert(0,t[-j]-(i+1)*l)
    dft_sin=[] #正弦傅里叶变换
    dft_cos=[] #余弦傅里叶变换
    dft=[]
    omega=np.arange(omega[0],omega[1],omega[2]) #离散频率
    for i in range(len(omega)):
        v1=0;v2=0;v3=0
        for j in range(len(T)-1):
            v1+=0.5*(S[j]+S[j+1])*dt*np.sin(-omega[i]*T[j])
            v2+=0.5*(S[j]+S[j+1])*dt*np.cos(-omega[i]*T[j])
            v3+=np.sqrt(v1**2+v2**2)
        dft_sin.append(v1)
        dft_cos.append(v2)
        dft.append(v3)
    return (dft,dft_sin,dft_cos)

以sin(5x)+sin(20x)+cos(10x)+cos(15x)信号为例。连续信号与采样离散信号如下所示。

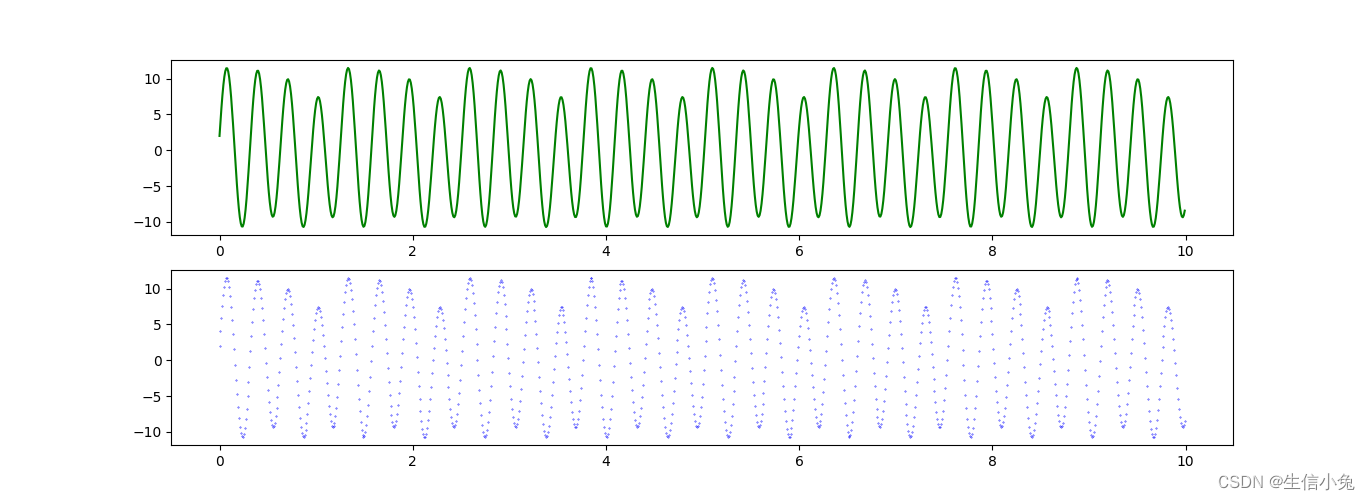
x=np.arange(0,10,0.01)
y=np.sin(5*x)+np.cos(15*x)+10*np.sin(20*x)+np.cos(10*x)
dft,dft_sin,dft_cos,omega=dft1(s=y,t=x,repet=[6,6],omega=[-25,25,0.1])

结果如下。

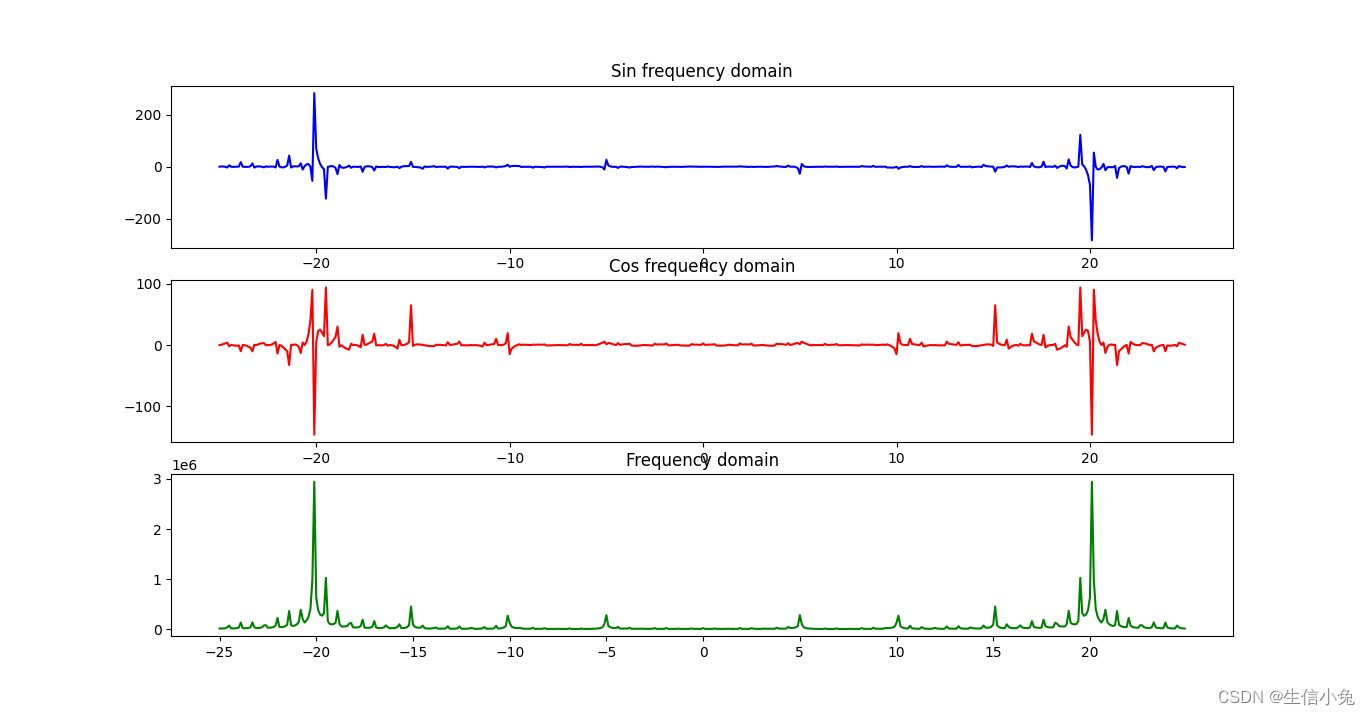
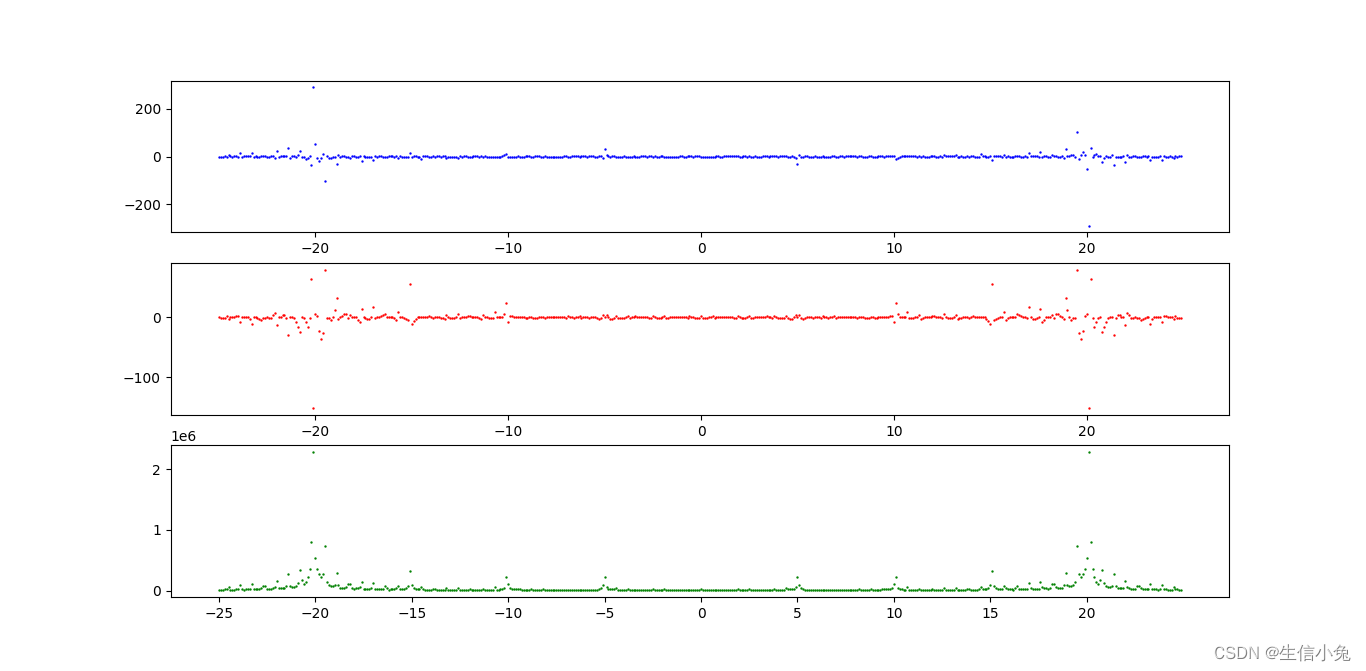
我们发现最终的结果与事实较为符合，正弦频域在5、20处出现峰，余弦频域在10、15处出现峰。但是余弦频域中频率20出现峰是不太合理的。并且使用该方法计算速度较慢，准确度也比较低。

（3）DFT算法

DFT算法表达式如下：

$X(\omega)=\sum_{n}x(n)e^{-i\omega n}$

其实x(n)为时序信号离散序列，X(ω)表示频域信号离散序列。并且与前面相同，利用欧拉公式可以得到正弦频域与余弦频域计算公式。兔兔在这里不在赘述。

def DFT(x,t,omega):
    n=len(x)
    X=[]
    omega=np.arange(omega[0],omega[1],omega[2])
    for i in range(len(omega)):
        s=0
        for j in range(n):
            s+=x[j]*np.exp(-1j*omega[i]*t[j])
        X.append(abs(s)) #求复数的模
    return (omega,X)

仍以前面的离散信号为例。

x=np.arange(0,10,0.01)
y=np.sin(5*x)+np.cos(15*x)+10*np.sin(20*x)+np.cos(10*x)
omega,X=DFT(x=y,t=x,omega=[-25,25,0.05])
plt.plot(omega,X,color='green')
plt.xticks(np.arange(-25,25,5))
plt.show()

结果如下所示

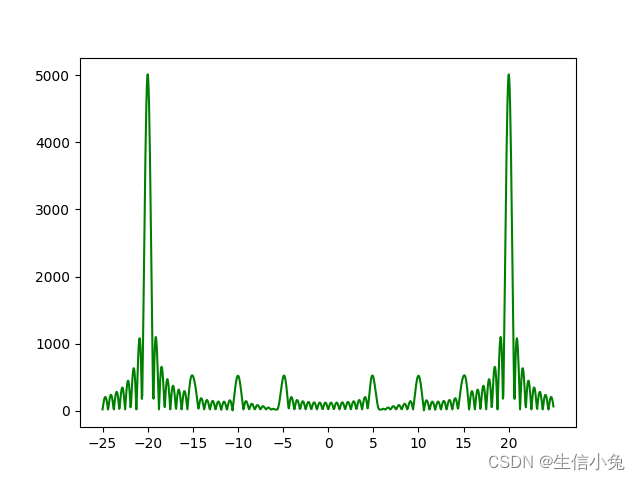
此时程序运行时间较短，并且准确率较高。

总结

针对离散时序序列的傅里叶变换，本文通过傅里叶的原始定义，初步设计一种能够进行离散数据傅里叶变换的方法，但由于其运算速度慢、准确率低，所以引入了DFT算法。DFT算法虽然效果较好，运算速度较快，但对于较长序列，计算仍是需要较多的时间。FFT算法的出现很好地解决该问题，它仍是以DFT算法为基础，对该算法进行一定的改进，并衍生多种FFT算法。所以如今FFT是计算离散傅里叶变换最常用的方法，而在numpy、scipy等模块中也都有实现FFT算法的方法，可以很方便地解决相关实际问题。