PID控制电机

控制系统

闭环

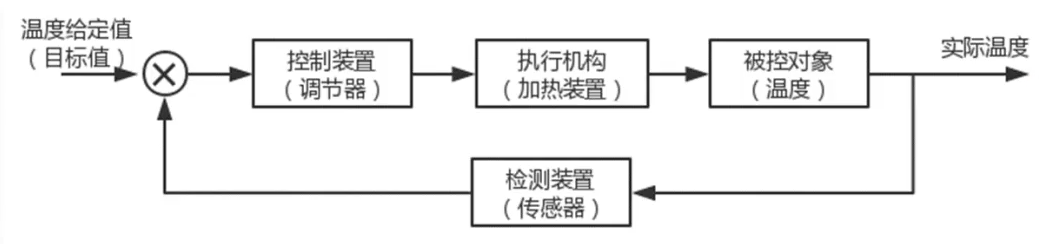
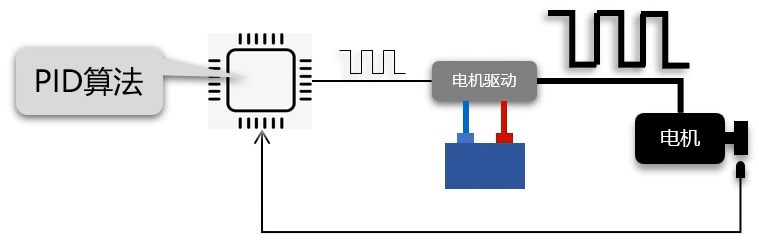
将PID算法的输出转化为PWM控制信号，发送给电机驱动电路，电机驱动电路与直流电机相连，并且会将PWM控制信号转化为相同占空比的PWM供电电压，通过对供电电压的PWM占空比的调节，实现对电机转速的调节。同时系统需要一个传感器，对电机状态进行定时采样，并将采样结果，作为反馈信号输入给单片机

 PID

连续表达式

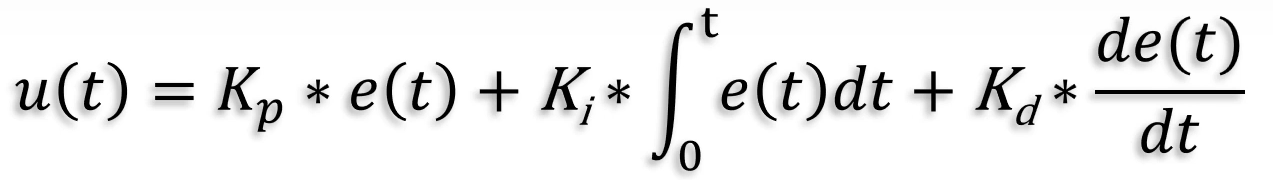
这是电机转速的连续变化曲线，用一个传感器沿着时间轴，对转速曲线进行逐点采样，采样间隔时间恒定为Δt，然后用这些采样点来近似表示，原来的连续曲线，这就是离散化过程。

P连续表达式

e(t）表示被控对象的当前状态，与目标状态的状态偏差。

 

离散化之后，P的离散表达式

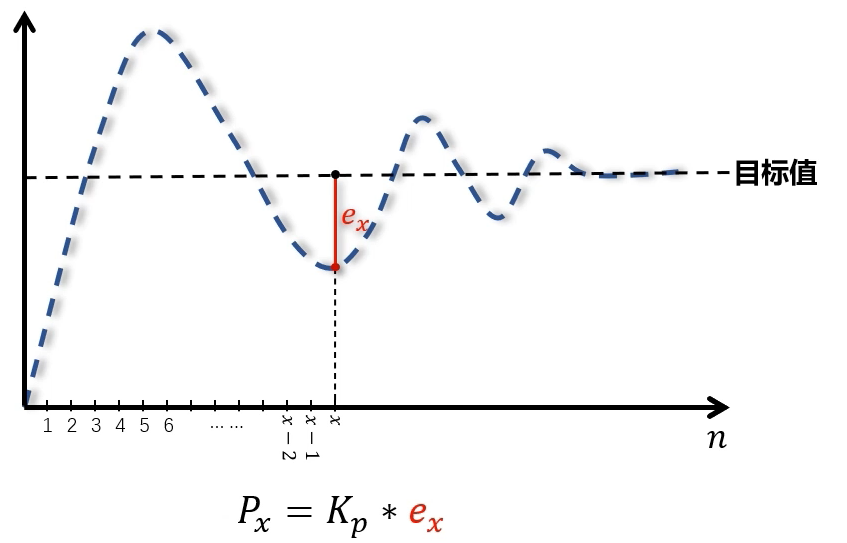
ex同样表示X点的状态值与目标状态值的偏差。

I连续表达式

积分部分表示0~t 时刻，对状态偏差的积分。在图中可以表示为这三部分的面积之和

离散化之后，I 的离散表达式

ex表示X采样点的状态偏差，Δt表示采样间隔，这两者相乘表示这部分的矩形面积。将1~X点的所有矩形面积相加，就得到了I 的离散表达式。

D连续表达式

de(t)/dt表示T时刻，状态偏差的微分。

离散化之后，D的离散表达式

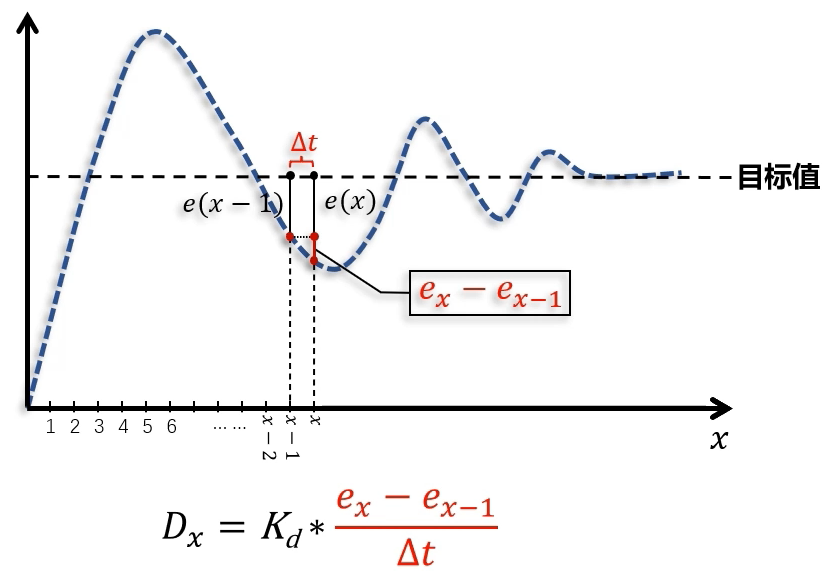
斜率，dt==Δt

离散表达式

Δt是常量，因此可以和比例系数Kp，微分系数Kd合并

得到位置式PID

之后

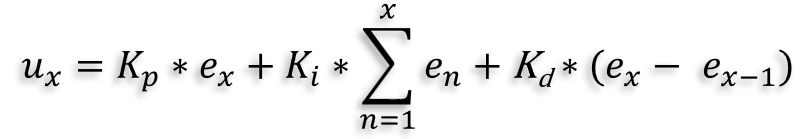
Ux为当前点的PID表达式，Ux-1为前一点的表达式。

用Ux - Ux-1，得到增量式PID

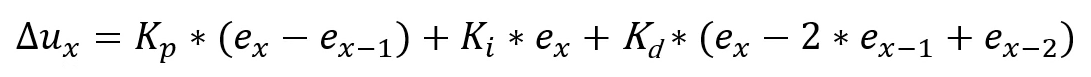
即

所以位置式和增量式，在本质上是同一个公式，只是两种不同的表达方式。

PID的作用

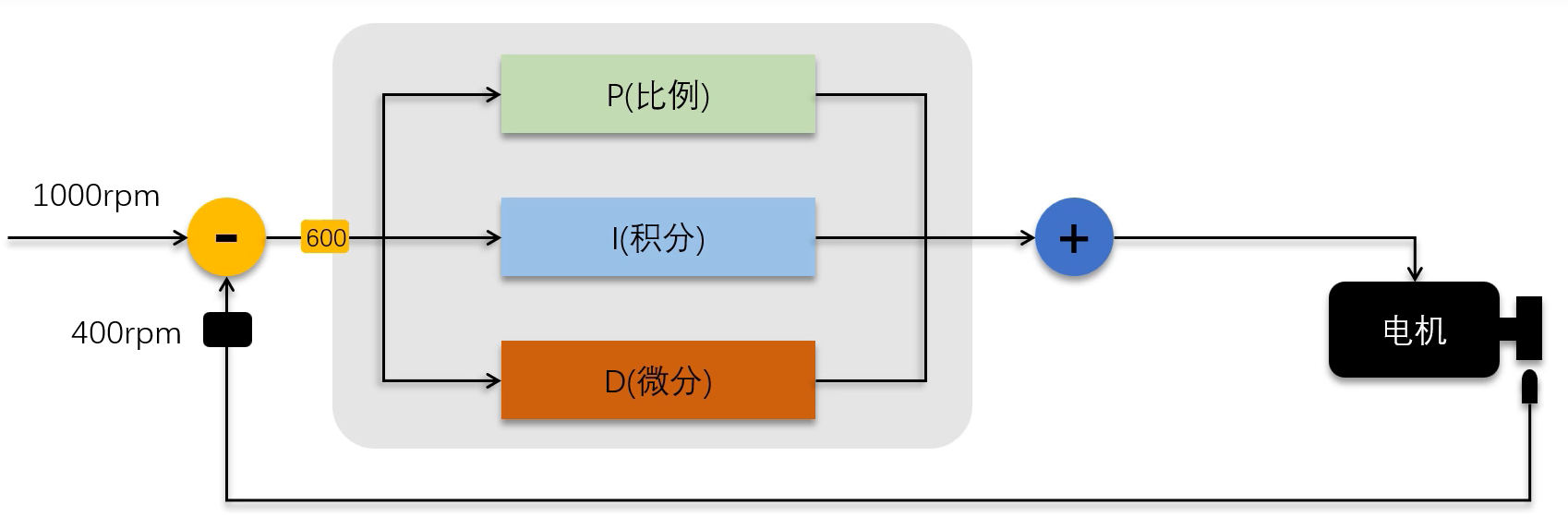
 et偏差值=目标值-当前值，第一次采样，第二次采样...所以t=1，t=2...

P：提高响应速度，减少稳态误差

当用P作为控制器，来控制电机时得到的转速曲线

随着系数Kp的增加，转速曲线的波动越来越陡峭，波峰也越来越高。

存在稳态误差，因为外部的干扰使得比例提供的控制量和外部因素抵消，导致实际控制量等于0了。可以理解为要一杯水一直维持在50度，但是当前温度为40，因为加热器的比例控制等输出功率输出跟水的散热正好抵消了，所以还需要一个ki来补偿。

随着系数Kp的增加，稳态偏差会逐渐缩小，但是始终无法消除。

当Kp过大时，会产生震荡。因为当转速达到目标值时，不控制，但由于惯性，转速还会继续上升一会。等转速低于目标值时，由于惯性，转速还会往下降。循环往复

波动是因为惯性，误差是因为系统自身存在一定阻力。

D可以减少波动

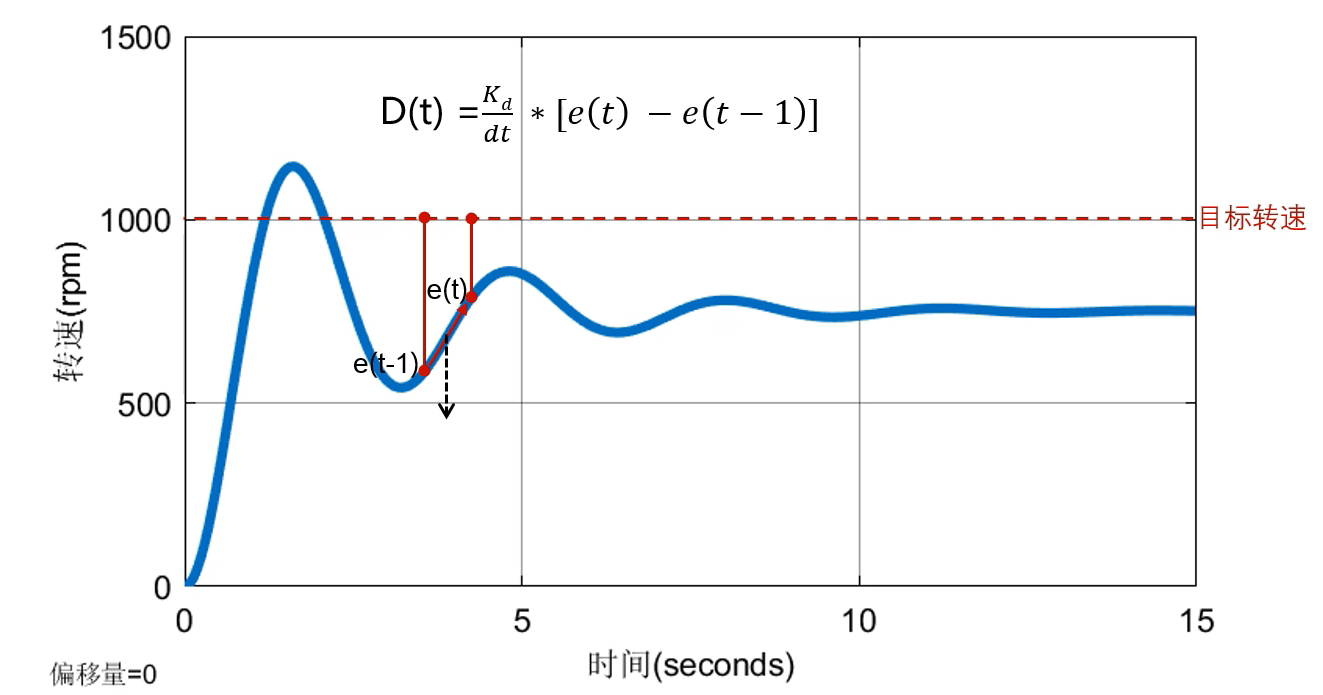
当e(t)-e(t-1)>0时，当前转速<上一点转速，D(t)>0，增加转速

当e(t)-e(t-1)<0时，当前转速>上一点转速，D(t)<0，减少转速

D像一个阻尼器，转速远离目标值的时候，它阻止远离；转速靠近目标值的时候，它阻止靠近。从而让被控对象更快地稳定在一个状态，不波动

I 解决稳态误差

系统稳定后存在稳态误差，加入I 后，I会对这部分误差进行正向积分，因为历史上的偏差之和没达标，积分项会增大输出，超过目标值（超调量偏大）

当转速超过目标转速时，I会对这部分误差进行负向积分，I(t)<0，减小转速。只要转速没有运行在目标转速上，I 就会发挥调节作用。被控对象最终会稳定在目标转速上

使用

Ut=Kp*e(t)，Kp像一个衰减器或放大器，用来调整传感器传回来的偏差值，把偏差值放大或缩小。

比例算法，特点是输出信号的大小与当前的偏差值成比例，偏差越大，输出的控制信号越大。

有缺陷：一旦传感器传回来的值与目标值相等，输出信号就等于0，不控制了，负载就处于失控状态，因此它由于外部的阻力，又会产生偏差。所以比例控制是一个始终有误差的控制算法，你没有误差我就不控制了，有了误差我才控制。

积分算法，Ut=Ki*(e1+e2+...+et-1+et)，特点是考虑了过去那段时间的状态，当过去那段时间总体大于0，没达标，则加大控制信号；反之超标，减小控制信号。

有缺陷：当过去的数据之和总体等于0，输出信号也等于0，只要历史上总体是好的，就是好的，会导致历史情况严重干扰了当前的情况。

所以PID的基本思想就是，我要通过历史上的这些数据，来预测出控制对象有可能发生的变化，我提前做控制，不要等到问题出现的时候再来控制。

微分算法，Ut=Kd*(Ek-Ek-1)，只考虑最近两次的偏差，表示偏差的一个变化趋势。当偏差之差>0时，，说明偏差有增大的趋势，需要加大控制输出。线越陡变化越剧烈；当偏差之差<0时，，偏差有减小的趋势，控制输出可以减小一点。

有缺陷：当偏差之差=0，偏差变化率是条直线，偏差始终存在，但偏差没有变大或变小的趋势。它只关心偏差有没有变化趋势，而不考察偏差存不存在。

通过最近这段时间的变化趋势，来预测将来的变化。Kd使斜率变大，控制的灵敏度变高。