一、SVM概念
SVM是一种二类分类模型(用于分类和回归分析的监督学习算法),其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。SVM大致可分为两种:
- 线性SVM
- 非线性SVM(需要核函数的支持)
二、SVM原理
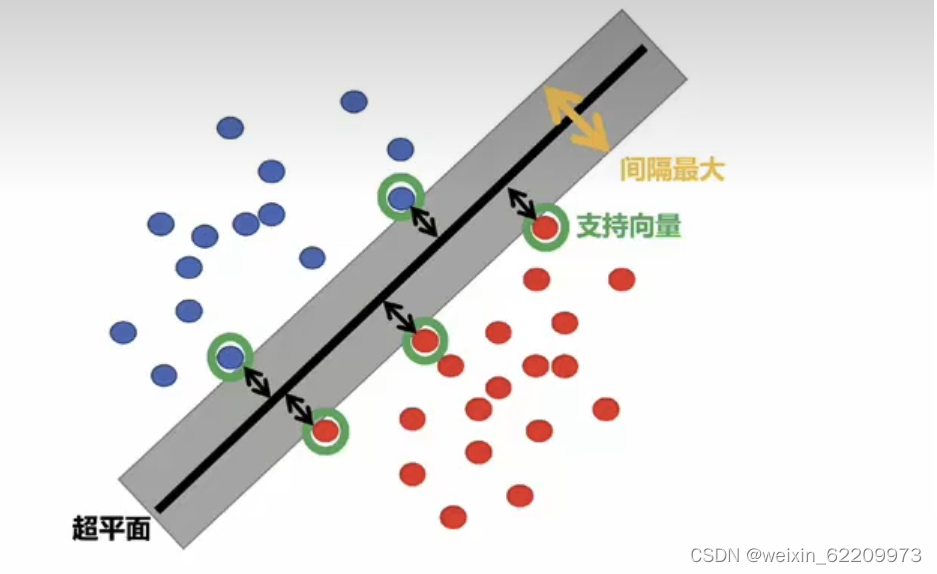
1.关键点
-
最大间隔:SVM的目标是找到一个能够最大化不同类别样本之间间隔的超平面。这意味着该超平面能够尽可能地远离最近的训练样本点,从而具有更好的泛化性能。
-
分类决策边界:SVM通过一个决策边界来划分不同类别的样本。对于二分类问题,决策边界可以是一个超平面,在特征空间中将正类和负类样本分开。SVM的目标是找到一个最优的决策边界,使得离该边界最近的样本点距离最大。
-
支持向量:在训练过程中,SVM选择距离决策边界最近的一些样本点作为支持向量。它们对于定义决策边界起到重要的作用,决定了分类器的性能。支持向量在SVM的优化问题中起到了关键的作用。
-
核函数:SVM可以使用核函数将样本点映射到高维特征空间中,使得在原始特征空间中线性不可分的问题可以在特征空间中变得线性可分。常用的核函数有线性核、多项式核和高斯核等。通过选择适当的核函数,SVM可以处理更加复杂的分类问题。
2.超平面
在机器学习中,SVM(支持向量机)中的超平面是用于分类的决策边界。对于二分类问题,超平面是一个(d-1)维的线性子空间,其中d是特征空间的维度。它将特征空间划分为两个部分,分别属于不同类别的样本点。
在二维空间中,超平面是一条直线,将特征空间分割为两个区域,分别对应于不同的类别。而在三维空间中,超平面是一个平面。在更高维度的特征空间中,超平面是一个超曲面。
SVM的目标是找到一个最优的超平面,使得离该超平面最近的训练样本点的距离最大化。通过最大化间隔,SVM能够提高分类器的泛化能力,使其对未知样本的分类具有较好的性能。
超平面可以由以下形式的线性方程表示:
其中,w是超平面的法向量,决定了超平面的方向;b是偏置项,控制了超平面与原点的距离。
3.朗格朗日对偶问题
在支持向量机(SVM)的优化问题中,使用拉格朗日乘子法将原始优化问题转化为拉格朗日对偶问题。推导过程:
-
原始问题:给定训练样本集合{(x1, y1), (x2, y2), ..., (xm, ym)},其中xi为特征向量,yi为对应的类别标签(+1或-1)。原始问题的目标是找到一个超平面,以最大化类别之间的间隔,并且正确分类训练样本。
- 超平面的表达式为
,其中w为超平面的法向量,b为偏置项。
- 类别之间的间隔可以表示为2/||w||,其中||w||为w的范数。
- 超平面的表达式为
-
引入拉格朗日乘子:为了将约束条件引入原始问题,我们使用拉格朗日乘子αi来对每个样本进行加权。加权后的目标函数可以表示为:L(w, b, α) = 1/2 * ||w||^2 - Σ[αi * (yi * (w·xi + b) - 1)]
-
求解对偶问题:通过最小化L(w, b, α)关于w和b的变量来最大化L(w, b, α)关于α的变量。首先对w和b求偏导,并令其等于0,可以得到:w = Σ[αi * yi * xi] Σ[αi * yi] = 0
将w代入L(w, b, α)中,我们可以得到拉格朗日对偶函数: L_D(α) = Σ[αi] - 1/2 * Σ[Σ[αi * αj * yi * yj * xi·xj]]
对偶问题的目标是最大化L_D(α)关于α的变量,且满足条件0 ≤ αi ≤ C,其中C是一个正则化参数。
4.KKT条件
KKT条件(Karush-Kuhn-Tucker条件)是最优化问题中的一组必要条件,用于判断是否找到了最优解。在支持向量机(SVM)中,KKT条件可以用于检验解是否满足约束条件,并判断是否存在支持向量。下面是SVM中的KKT条件:
非负性条件:对所有的i,都有。
互补松弛条件:对所有的i,都有yi(f(xi) - b) ≥ 1 - ε - ξi和αiξi = 0。
对偶互补条件:对所有的i,都有αi[yi(f(xi) - b) - 1 + ξi] = 0。
原始可行性条件:对所有的i,都有yi(f(xi) - b) ≤ 1 - ε和ξi ≥ 0。
对偶可行性条件:对所有的i,都有αi ≥ 0。
其中,αi是拉格朗日乘子,f(xi)是样本xi的预测值,b是超平面的截距项,ε是松弛变量的上界,ξi是松弛变量。
5.核函数
在支持向量机(SVM)中,核函数是一种用于处理非线性问题的技术。它通过将数据映射到高维特征空间中,使得原本线性不可分的样本在新的特征空间中变得线性可分。核函数可以将内积运算替换为更高维度的计算,从而减少计算复杂度。
高斯核函数的表达式为:
其中,是一个决定衰减速率的参数。
假设有两个样本点x = [1, 2]和y = [3, 4],我们可以使用高斯核函数计算它们之间的相似性:
这里的||x-y||表示欧氏距离,即。
如果我们取γ = 0.5,那么计算结果如下:
K(x, y) = exp(-0.5 * 8) ≈ 0.082
这个值表示样本点x和y之间的相似性程度,可以用于支持向量机等机器学习算法中的分类或回归任务。
三、SVM的Python实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm, datasets
class SVMVisualizer:
def __init__(self):
self.X = None
self.y = None
self.clf = None
def generate_dataset(self):
self.X, self.y = datasets.make_classification(n_samples=1000, n_features=2, n_redundant=0, n_informative=2, random_state=1, n_clusters_per_class=1)
def train_svm(self):
self.clf = svm.SVC(kernel='linear', C=1)
self.clf.fit(self.X, self.y)
def visualize(self):
plt.scatter(self.X[:, 0], self.X[:, 1], c=self.y, cmap=plt.cm.Paired)
plt.axis('tight')
x_min, x_max = self.X[:, 0].min(), self.X[:, 0].max()
y_min, y_max = self.X[:, 1].min(), self.X[:, 1].max()
XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
Z = self.clf.decision_function(np.c_[XX.ravel(), YY.ravel()])
Z = Z.reshape(XX.shape)
plt.contourf(XX, YY, Z, cmap=plt.cm.Paired, alpha=0.8)
plt.colorbar()
plt.show()
# 创建 SVMVisualizer 对象
svm_visualizer = SVMVisualizer()
# 生成随机二分类数据集
svm_visualizer.generate_dataset()
# 训练支持向量机模型
svm_visualizer.train_svm()
# 可视化数据集和支持向量机模型的决策边界
svm_visualizer.visualize()输出:
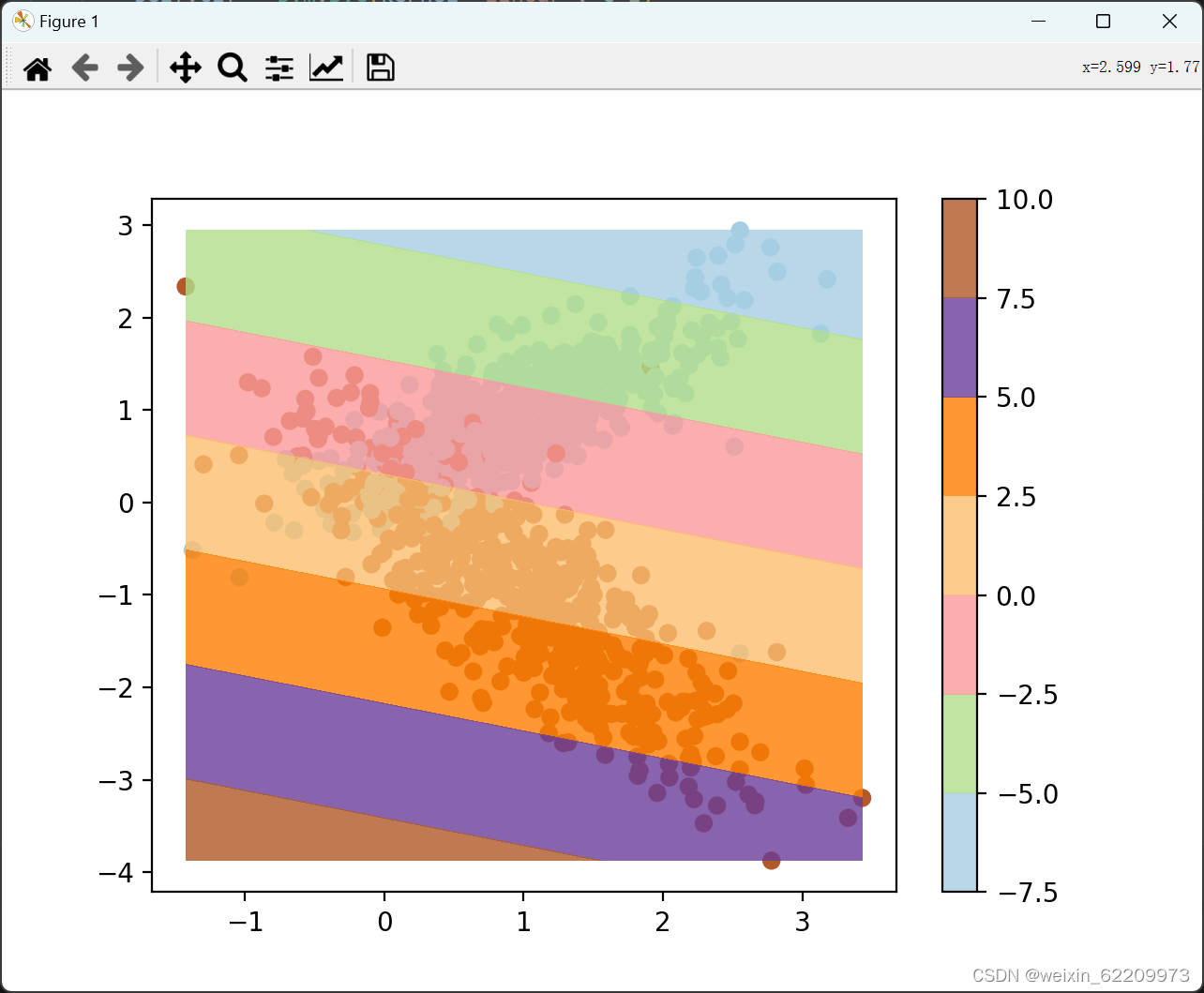





















 499
499











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








