【机器学习】吴恩达课程2-单变量线性回归

已于 2024-10-06 15:19:38 修改
阅读量355 收藏
点赞数 1
分类专栏： 机器学习 文章标签： 机器学习 线性回归 人工智能
于 2023-07-17 15:54:40 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_62403234/article/details/131739551
版权

一、单变量线性回归

 1. 模型描述

监督学习的流程 & 单变量线性回归函数

代价函数：J(\theta_{0},\theta_{1})=\frac{1}{2m}\sum_{i=1}^{n}(h(x^{(i)})-y^{(i)})^{2}，其中 m 表示训练样本的数量

公式为预测值与实际值的差，平方为最小二乘法和最佳平方/函数逼近。

目标：最小化代价函数，即minimize J(\theta_{0},\theta_{1})

2. 只考虑一个参数 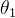\theta_{1}

为方便分析，先取\theta_{0}为0并改变\theta_{1}的值

在这里插入图片描述

 3. 参数 \theta_{0}\theta_{1} 都考虑

在这里插入图片描述

 将三维图平面化：等高线的中心对应最小的代价函数

在这里插入图片描述

二、梯度下降

1. 算法思路

  • 指定 \theta_{0}  和 \theta_{1} 的初始值
  • 不断改变 \theta_{0} 和 \theta_{1} 的值，使 J(\theta_{0},\theta_{1}) 不断减小
  • 得到一个最小值或局部最小值时停止

2. 梯度

函数中某一点(x, y)的梯度代表函数在该点变化最快的方向（选用不同的点开始可能达到另一个局部最小值）

在这里插入图片描述

\theta _{j}:= \theta _{j}-\alpha \frac{dJ(\theta _{i},\theta _{j})}{d\theta _{j}}

关于α：选择太小，会导致每次移动的步幅都很小，最终需要很多步才能最终收敛；
             选择太大，会导致每次移动的步幅过大，可能会越过最小值，无法收敛甚至会发散；

实现原理：偏导表示的是斜率，斜率在最低点左边为负，最低点右边为正。\theta _{j} 减去一个负数则向右移动，减去一个正数则向左移动。在移动过程中，偏导值会不断变小，进而移动的步幅也不断变小，最后不断收敛直到到达最低点。在最低点处偏导值为0，不再移动。

2.3 线性回归的梯度下降 / Batch梯度下降

最小化线性回归中的平方损失函数。

 同时更新：

提示：

凸函数（convex function）：只要一个全局最优

批量梯度下降：每次梯度下降使用所有的训练样本

禾风wyh
关注
专栏目录
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值