机器学习之Logistic回归

衍浒

于 2023-12-04 21:18:06 发布

阅读量104

点赞数

文章标签：机器学习回归人工智能

本文链接：https://blog.csdn.net/weixin_63094874/article/details/134792557

版权

一、逻辑斯蒂回归（Logistic Regression）概念

一、逻辑斯蒂回归（Logistic Regression）概念

逻辑斯蒂回归，相当于线性回归加上sigmoid激活函数，把数据映射到了0，1之间，更方便计算损失函数。

逻辑斯蒂回归（Logistic Regression）是一种用于解决二分类问题的机器学习算法。它通过建立一个逻辑斯蒂函数（Logistic Function）来估计因变量属于某个类别的概率。

逻辑斯蒂回归的核心思想是将线性回归模型的输出映射到[0,1]区间，表示观测样本属于某个类别的概率。

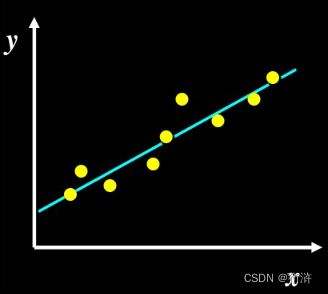
逻辑斯蒂函数（也称为Sigmoid函数）可以实现这种映射，其公式为：

P(Y=1|X) = 1 / (1 + e^-(β0 + β1X1 + β2X2 + ...+ βpXp))

其中，P(Y=1|X)表示在给定自变量X的条件下，因变量Y等于1的概率。β表示模型参数，X表示自变量的特征，e表示自然对数的底。

逻辑斯蒂回归的训练过程就是通过最大似然估计或梯度下降等方法，寻找最优的模型参数β，使得模型对数据的拟合度最高。一旦训练完成，我们可以使用该模型对新的样本进行分类预测。

逻辑斯蒂回归具有以下特点：

1.可以处理二分类问题，即将样本分为两个类别。
2.输出结果是一个概率值，表示样本属于某个类别的概率。
3.基于线性模型，易于理解和解释。
4.通常使用最大似然估计等优化算法进行参数估计。
5.逻辑斯蒂回归在实际应用中被广泛使用，例如垃圾邮件识别、疾病预测、信用评分等场景。

它是一种简单而有效的分类算法，但也有一定的局限性，例如对于非线性可分的问题，逻辑斯蒂回归表现可能不佳，此时可能需要考虑其他更复杂的模型。

二、线性模型与回归

逻辑斯蒂回归是一种广泛应用于二分类问题的机器学习模型，它基于线性模型和回归理论。

首先来说一下线性模型。在统计学中，线性模型是一种用于建立变量之间线性关系的一类模型。它可以用来预测因变量Y对自变量X的影响关系。线性回归模型的公式为：

Y = β0 + β1X1 + β2X2 + ...+ βpXp + ε

其中，Y是因变量，X是自变量，β是模型参数，ε是误差项。线性回归模型的目标是最小化残差平方和，即寻找最优的β值，从而使得模型的预测值与真实值之间的误差最小。

接下来说一下回归。回归分析是一种用于研究变量之间关系的方法。在机器学习中，回归分析是一种用于预测连续变量的模型。回归分析可以分为线性回归和非线性回归两种。线性回归是指因变量和自变量之间的关系是线性的，而非线性回归是指它们之间的关系是非线性的。在回归分析中，我们通常使用最小二乘法来确定模型参数，使得预测值和真实值之间的误差最小。

逻辑斯蒂回归模型是一种基于线性模型的分类方法。它将线性回归模型中的因变量Y扩展到了[0,1]之间，从而可以用来进行二分类问题的建模。逻辑斯蒂回归模型的公式为：

P(Y=1|X) = e^(β0 + β1X1 + β2X2 + ...+ βpXp) / (1 + e^(β0 + β1X1 + β2X2 + ...+ βpXp))

其中，P(Y=1|X)表示在给定自变量X的条件下，因变量Y等于1的概率。该模型的目标是最小化损失函数，从而找到最优的模型参数β值。通常采用最大似然估计来确定模型参数，使得模型对数据的拟合度最高。

总之，逻辑斯蒂回归是一种基于线性模型和回归理论的分类方法，它通过将因变量扩展到[0,1]之间，可以用于二分类问题的建模，并且通常采用最大似然估计来确定模型参数。

逻辑回归通常用于处理二分类问题的数据，其中每个样本都有一组特征和一个二元标签（0或1）。这些特征可以是连续的，也可以是离散的，逻辑回归都能够处理。例如，我们给出西瓜的 [甜度，大小] 这两个指标，然后判断一个西瓜是属于“好瓜”还是”怀瓜“这一类。对于这个问题，我们可以先测量n个西瓜的甜度及重量以及对应的指标”好瓜“、"怀瓜”，把好瓜和坏瓜分别用0和1来表示，把这n组数据输入模型进行训练。训练之后再把待分类的瓜的甜度和重量输入模型中，看这个瓜是属于“好瓜”还是“坏瓜”。

三、最小二乘与参数求解

逻辑斯蒂回归（Logistic Regression）是一种用于二分类问题的常见机器学习算法。与线性回归不同，逻辑斯蒂回归的目标是预测一个二元变量（0或1），因此在模型中使用了一个逻辑函数（Sigmoid函数）将线性函数的输出转换为概率值。

最小二乘法不适用于逻辑斯蒂回归的参数求解，因为逻辑斯蒂回归的目标函数不是凸函数，无法得到全局最优解。因此，通常采用最大似然估计（Maximum Likelihood Estimation，MLE）来求解逻辑斯蒂回归的参数。

在逻辑斯蒂回归中，假设样本的标签 (y_i) 是根据一个概率分布生成的（即服从伯努利分布），其概率密度函数为：

[ P(y_i | x_i, \theta) = \begin{cases} h_{\theta}(x_i), & \text{if } y_i=1 \ 1- h_{\theta}(x_i), & \text{if } y_i=0 \end{cases} ]

其中，( h_{\theta}(x_i) ) 是逻辑函数（sigmoid函数），其定义为：

[ h_{\theta}(x_i) = \frac{1}{1 + e^{-\theta^T x_i}} ]

而我们的目标是找到一组参数 ( \theta )，使得样本标签的概率分布最符合观测到的数据。因此，我们的目标函数可以表示为：

[ L(\theta) = \prod_{i=1}^{m} P(y_i | x_i, \theta) = \prod_{i=1}^{m} [h_{\theta}(x_i)]^{y_i} [1-h_{\theta}(x_i)]^{1-y_i} ]

通常，我们会使用对数似然函数来求解最大化目标函数：

[ \ell(\theta) = \log L(\theta) = \sum_{i=1}^{m} y_i \log h_{\theta}(x_i) + (1-y_i) \log (1 - h_{\theta}(x_i)) ]

最大化对数似然函数等价于最小化负对数似然函数，因此我们的目标是找到使得负对数似然函数最小的参数 ( \theta )。这可以通过梯度下降等优化算法求解。

总之，逻辑斯蒂回归通常采用最大似然估计来求解模型的参数，其目标是最大化样本标签的概率分布与观测数据之间的相似度。这种方法可以通过梯度下降等优化算法来实现。

四、对数线性回归

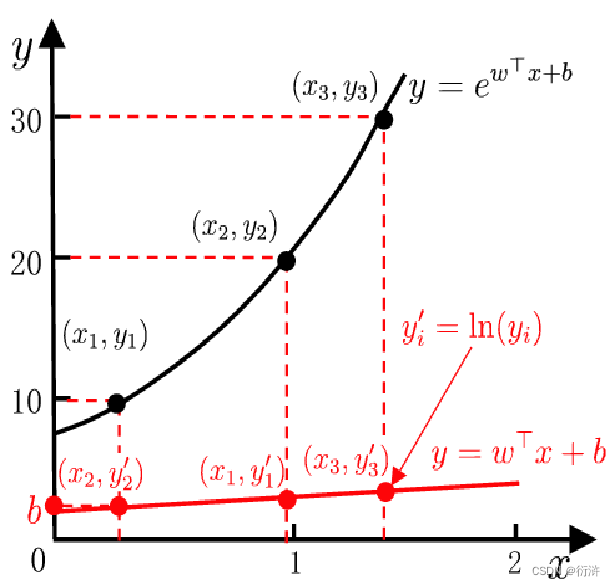
线性回归模型：f(x)=wx+b，取合适的w，b值，使得预测值逼近真实标记 y。

线性回归模型： y=f(x)=wx+b 可推广至： y=g(f(x))=g(wx+b) 其中g为单调可微函数

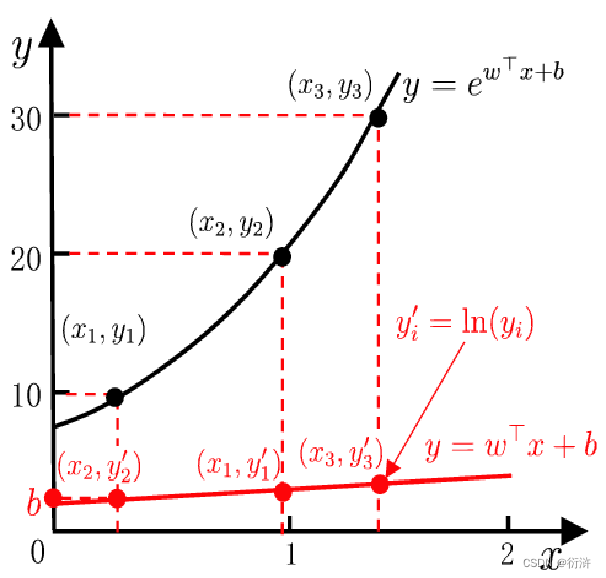
例如设g(x)=ex，取y的对数，即lny，就可以得到对数线性回归模型：

$y=e^{wx+b}\Leftrightarrow lny=wx+b$

同理

$lny=w^{T}x+b\Leftrightarrow y=e^{w^{T}x+b}$

五、Logistic回归

1.分类问题

逻辑斯蒂回归（Logistic Regression）是一种常用的机器学习算法，特别适用于二分类问题。它通过建立一个逻辑函数（Sigmoid函数）来对样本进行分类。

对于二分类问题，我们假设样本的标签 (y_i) 是0或1，并且在逻辑斯蒂回归中，我们希望预测样本属于某个类别的概率。

假设有一个训练集包含 (m) 个样本，每个样本的特征向量为 (x_i)，对应的标签为 (y_i)。我们的目标是找到一个合适的模型参数 (\theta)，使得对于给定的特征向量 (x_i)，可以预测其属于类别1的概率。

逻辑斯蒂回归使用一个逻辑函数（Sigmoid函数）将线性函数的输出转换为概率值。该函数定义如下：

[ h_{\theta}(x_i) = \frac{1}{1 + e^{-\theta^T x_i}} ]

其中，( h_{\theta}(x_i) ) 表示样本 (x_i) 属于类别1的概率，(\theta) 是模型的参数，( \theta^T ) 表示参数的转置。

在训练阶段，需要确定最优的模型参数 (\theta)。通常，我们会使用最大似然估计（Maximum Likelihood Estimation，MLE）来求解参数。通过最大化观测数据的似然函数可以找到最适合样本数据的模型参数。

在预测阶段，对于一个新的样本特征向量 (x)，我们可以使用训练得到的模型参数 (\theta) 来计算其属于类别1的概率 ( h_{\theta}(x) )。如果概率值大于等于一个预先设定的阈值（通常为0.5），将样本划分为类别1；否则，将其划分为类别0。

2.极大似然法

对于逻辑斯蒂回归（Logistic Regression），可以使用极大似然估计（Maximum Likelihood Estimation，MLE）来求解模型的参数。极大似然法是一种常用的参数估计方法，它通过找到使观测数据的概率最大化的参数值来估计模型参数。

在逻辑斯蒂回归中，假设样本的标签 (y_i) 是根据一个二元分布生成的，其中标签为1的概率为 (h_{\theta}(x_i))，标签为0的概率为 (1 - h_{\theta}(x_i))。我们的目标是找到一组参数 (\theta)，使得样本标签的概率分布最符合观测到的数据。

假设有 (m) 个独立同分布的样本数据，其中第 (i) 个样本的特征向量为 (x_i)，标签为 (y_i)。那么样本数据的似然函数（likelihood function）可以表示为：

[ L(\theta) = \prod_{i=1}^{m} [h_{\theta}(x_i)]^{y_i} [1-h_{\theta}(x_i)]^{1-y_i} ]

通常，我们会使用对数似然函数（log-likelihood function）来求解最大化问题，因为对数函数具有更好的数学性质：

[ \ell(\theta) = \log L(\theta) = \sum_{i=1}^{m} y_i \log h_{\theta}(x_i) + (1-y_i) \log (1 - h_{\theta}(x_i)) ]

目标是找到使得对数似然函数最大化的参数值 (\theta)。为了实现这一点，我们可以使用优化算法（如梯度下降、牛顿法等）来最大化对数似然函数。

具体来说，在求解过程中，需要计算对数似然函数关于参数 (\theta) 的梯度，并使用梯度上升或梯度下降等方法来迭代更新参数。通过迭代过程，我们可以逐步提高对数似然函数的值，直到达到最大化的目标。

3.梯度下降

在逻辑斯蒂回归中，我们的目标是最大化对数似然函数（log-likelihood function）来寻找最优的参数值。为了实现这一点，可以使用梯度下降来迭代更新参数，直到达到最大化的目标。

以下是逻辑斯蒂回归中梯度下降的步骤：

初始化参数：首先，我们需要初始化模型的参数 (\theta)。可以随机初始化参数，或者使用零向量初始化。

计算预测值：对于每个样本 (x_i)，计算其属于类别1的预测概率 (h_{\theta}(x_i))。

计算误差：计算预测值与实际标签之间的误差，通常使用对数似然函数作为损失函数。逻辑斯蒂回归的对数似然函数为：(\ell(\theta) = \sum_{i=1}^{m} y_i \log h_{\theta}(x_i) + (1-y_i) \log (1 - h_{\theta}(x_i)))。

计算梯度：计算对数似然函数关于参数 (\theta) 的梯度。梯度表示了目标函数在当前参数值处的变化率，可以用来指导参数的更新方向。对于逻辑斯蒂回归，梯度的计算公式为：(\frac{\partial \ell(\theta)}{\partial \theta_j} = \sum_{i=1}^{m} (h_{\theta}(x_i) - y_i) x_{ij})，其中 (x_{ij}) 表示第 (i) 个样本的第 (j) 个特征值。

更新参数：使用梯度乘以学习率（learning rate）来更新参数。学习率控制每次迭代中参数更新的步长，过大的学习率可能导致无法收敛，而过小的学习率可能导致收敛速度过慢。更新公式为：(\theta_j := \theta_j - \alpha \frac{\partial \ell(\theta)}{\partial \theta_j})，其中 (\alpha) 是学习率。

重复迭代：重复执行步骤2-5，直到达到收敛条件（如达到固定的迭代次数或参数变化小于某个阈值）。

通过梯度下降算法，可以逐步优化模型的参数，使得对数似然函数最大化，从而得到最优的逻辑斯蒂回归模型。

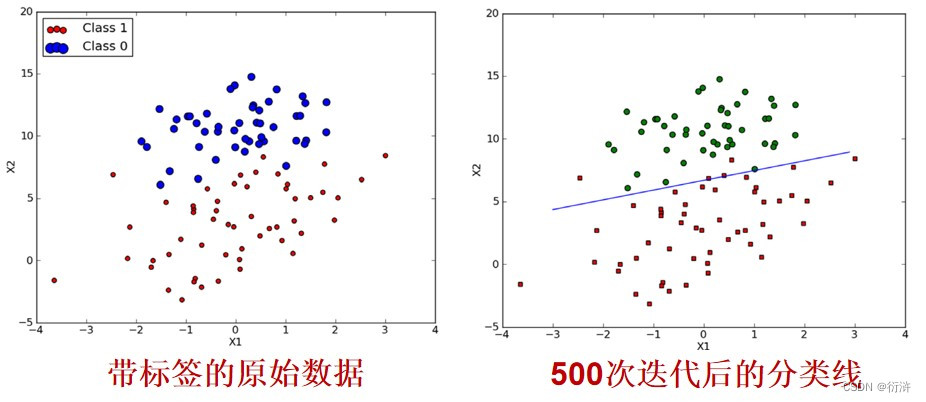
4.数据分类

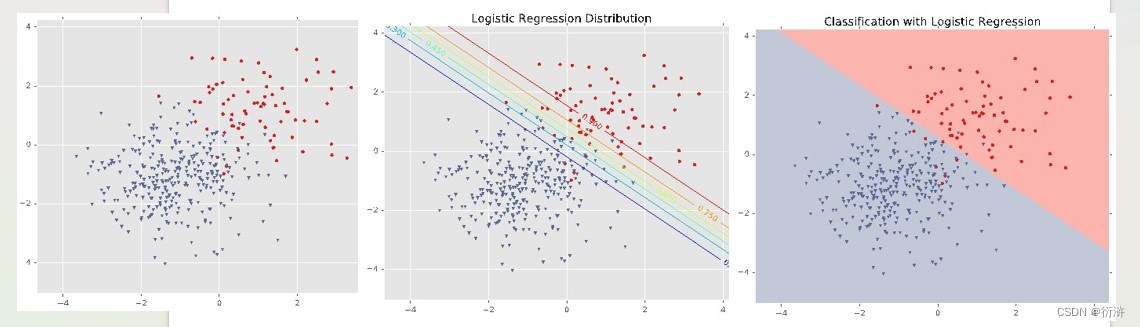
六、示例

1.准备数据
首先需要准备训练数据和测试数据。通常，我们将数据分为特征和标签两部分，其中特征是一个二维张量，形状为 (样本数, 特征数)，标签是一个一维张量，形状为 (样本数,)。可以使用 PyTorch 的 Tensor 类型来表示这些数据。

import torch

# 准备数据
X_train = torch.tensor([[1, 2], [3, 4], [5, 6], [7, 8]], dtype=torch.float32)
y_train = torch.tensor([0, 0, 1, 1], dtype=torch.float32)
X_test = torch.tensor([[2, 3], [4, 5], [6, 7]], dtype=torch.float32)
y_test = torch.tensor([0, 0, 1], dtype=torch.float32)

2.定义模型
接下来需要定义逻辑斯蒂回归模型。在 PyTorch 中，可以使用 nn.Module 类来定义模型，并在构造函数中定义模型的各个层，然后在 forward 方法中实现前向传播过程。

import torch.nn as nn

# 定义模型
class LogisticRegression(nn.Module):
    def __init__(self, input_size, output_size):
        super(LogisticRegression, self).__init__()
        self.linear = nn.Linear(input_size, output_size)

    def forward(self, x):
        out = self.linear(x)
        return out

在上述代码中定义了一个继承自 nn.Module 的 LogisticRegression 类，并在构造函数中定义了一个线性层。在 forward 方法中，我们将输入张量 x 传递给线性层，并返回输出张量 out。

3.定义损失函数和优化器
为了训练模型，需要定义损失函数和优化器。逻辑斯蒂回归的常用损失函数是二元交叉熵损失（binary cross entropy loss），可以使用 PyTorch 的 nn.BCEWithLogitsLoss 类来实现。优化器可以选择随机梯度下降（SGD）或 Adam 等常用优化器。

import torch.optim as optim

# 定义损失函数和优化器
criterion = nn.BCEWithLogitsLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

在上述代码中，使用了二元交叉熵损失和 SGD 优化器，学习率为 0.01。

4.训练模型
定义好模型、损失函数和优化器之后，就可以开始训练模型了。训练模型需要多次迭代数据集，并计算损失函数和梯度。在每个迭代周期结束时，可以打印损失值和模型精度等指标，以便监控训练过程。

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    # 前向传播
    outputs = model(X_train)
    loss = criterion(outputs, y_train)

    # 反向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # 打印损失值和精度
    if (epoch+1) % 100 == 0:
        with torch.no_grad():
            train_loss = criterion(model(X_train), y_train)
            train_acc = ((model(X_train) > 0.5).squeeze().long() == y_train.long()).sum().item() / y_train.size(0)
            test_loss = criterion(model(X_test), y_test)
            test_acc = ((model(X_test) > 0.5).squeeze().long() == y_test.long()).sum().item() / y_test.size(0)
            print(f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {train_loss.item():.4f}, Train Acc: {train_acc:.4f}, Test Loss: {test_loss.item():.4f}, Test Acc: {test_acc:.4f}')

在上述代码中，使用了一个 for 循环执行多次迭代。在每个迭代周期中，首先进行前向传播和计算损失函数。然后，使用 optimizer.zero_grad() 方法清除所有梯度，使用 loss.backward() 方法计算梯度，使用 optimizer.step() 方法执行一步优化。最后，在每个周期结束时，使用 with torch.no_grad() 上下文环境计算训练集和测试集的损失值和精度，并在控制台打印输出。

5.测试模型
训练好模型之后，可以使用测试数据集对模型进行测试，并计算模型的精度和其他指标。

# 测试模型
with torch.no_grad():
    outputs = model(X_test)
    predicted = (outputs > 0.5).squeeze().long()
    acc = (predicted == y_test.long()).sum().item() / y_test.size(0)
    print(f'Test Accuracy: {acc:.4f}')

在上述代码中，首先使用 with torch.no_grad() 上下文环境将模型设置为评估模式。然后，对测试数据进行前向传播，并使用一个阈值（0.5）将输出值转换为预测标签。最后，计算预测标签和真实标签之间的精度，并在控制台打印输出。

完整的示例代码如下：

import torch
import torch.nn as nn
import torch.optim as optim

# 准备数据
X_train = torch.tensor([[1, 2], [3, 4], [5, 6], [7, 8]], dtype=torch.float32)
y_train = torch.tensor([0, 0, 1, 1], dtype=torch.float32)
X_test = torch.tensor([[2, 3], [4, 5], [6, 7]], dtype=torch.float32)
y_test = torch.tensor([0, 0, 1], dtype=torch.float32)

# 定义模型
class LogisticRegression(nn.Module):
    def __init__(self, input_size, output_size):
        super(LogisticRegression, self).__init__()
        self.linear = nn.Linear(input_size, output_size)

    def forward(self, x):
        out = self.linear(x)
        return out

model = LogisticRegression(input_size=2, output_size=1)

# 定义损失函数和优化器
criterion = nn.BCEWithLogitsLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    # 前向传播
    outputs = model(X_train)
    loss = criterion(outputs, y_train)

    # 反向传播和优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # 打印损失值和精度
    if (epoch+1) % 100 == 0:
        with torch.no_grad():
            train_loss = criterion(model(X_train), y_train)
            train_acc = ((model(X_train) > 0.5).squeeze().long() == y_train.long()).sum().item() / y_train.size(0)
            test_loss = criterion(model(X_test), y_test)
            test_acc = ((model(X_test) > 0.5).squeeze().long() == y_test.long()).sum().item() / y_test.size(0)
            print(f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {train_loss.item():.4f}, Train Acc: {train_acc:.4f}, Test Loss: {test_loss.item():.4f}, Test Acc: {test_acc:.4f}')

# 测试模型
with torch.no_grad():
    outputs = model(X_test)
    predicted = (outputs > 0.5).squeeze().long()
    acc = (predicted == y_test.long()).sum().item() / y_test.size(0)
    print(f'Test Accuracy: {acc:.4f}')

七、小结

逻辑斯蒂回归是一种用于解决二分类问题的机器学习算法，它通过将输入特征线性组合，并经过一个 sigmoid 函数来预测样本属于某一类别的概率。

在实验过程中，完成了以下步骤：

1.准备数据：准备了训练数据和测试数据，并使用 PyTorch 的 Tensor 类型来表示这些数据。

2.定义模型：定义了一个继承自 nn.Module 的 LogisticRegression 类，并在构造函数中定义了一个线性层。在 forward 方法中，我们将输入张量传递给线性层，并返回输出张量。

3.定义损失函数和优化器：选择了二元交叉熵损失函数和随机梯度下降（SGD）优化器。

4.训练模型：使用多轮迭代的方式训练模型。在每个迭代周期中，进行前向传播、计算损失函数、反向传播和优化参数的过程。在每个周期结束时，计算训练集和测试集的损失值和精度，并打印输出。

5.测试模型：在训练好模型后，使用测试数据集对模型进行测试，并计算模型的精度。

逻辑斯蒂回归是一种简单而有效的分类算法，特别适用于二分类问题。然而，在实际应用中，我们可能需要处理更复杂的数据和模型，以及调整超参数来提高模型性能。因此，深入学习机器学习的相关知识，包括其他分类算法、特征工程、模型评估等方面，将有助于我们更好地应用和理解机器学习算法。

衍浒

关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
机器学习之Logistic回归

对于逻辑斯蒂回归，梯度的计算公式为：(\frac{\partial \ell(\theta)}{\partial \theta_j} = \sum_{i=1}^{m} (h_{\theta}(x_i) - y_i) x_{ij})，其中 (x_{ij}) 表示第 (i) 个样本的第 (j) 个特征值。在逻辑斯蒂回归中，假设样本的标签 (y_i) 是根据一个二元分布生成的，其中标签为1的概率为 (h_{\theta}(x_i))，标签为0的概率为 (1 - h_{\theta}(x_i))。
复制链接

扫一扫