第 9 章 搜索
9.1 宽(广)度优先搜索
例 9.1 Catch That Cow
题目大意

心得体会:

代码表示:
#include <bits/stdc++.h>
using namespace std;
struct info{
int pos;
int time;
};
int main(){
int n,k;
scanf("%d%d",&n,&k);
queue<info>posqueue;
bool isvisit[100001];
for(int i=0;i<100001;++i){//判断有没有被访问过
isvisit[i]=false;
}
//把起始点加入队列中
info first;
first.pos=n;
first.time=0;
posqueue.push(first);
while(posqueue.empty()==false){
info cur=posqueue.front();
posqueue.pop();
if(cur.pos==k){
printf("%d\n",cur.time);
break;
}
isvisit[cur.pos]=true;//标记一下表示已经加入了
//把邻居加入到队列中
info neighbour ;
if(cur.pos-1>=0&&cur.pos-1<=100000&&isvisit[cur.pos-1]==false){
neighbour.pos=cur.pos-1;
neighbour.time=cur.time+1;
posqueue.push(neighbour);
}
if(cur.pos+1>=0&&cur.pos+1<=100000&&isvisit[cur.pos+1]==false){
neighbour.pos=cur.pos+1;
neighbour.time=cur.time+1;
posqueue.push(neighbour);
}
if(cur.pos*2>=0&&cur.pos*2<=100000&&isvisit[cur.pos*2]==false){
neighbour.pos=cur.pos*2;
neighbour.time=cur.time+1;
posqueue.push(neighbour);
}
}
return 0;
}
例 Find The Multiple
题目大意

思路提示
使用广度优先,先尝试小的数字再尝试大的。

代码表示
#include <bits/stdc++.h>
using namespace std;
void BFS(int n) {
queue<long long> myQueue;
myQueue.push(1); // 压入初始状态
while (!myQueue.empty()) {
long long current = myQueue.front();//取出队首
myQueue.pop();//弹出队首
if (current % n == 0) { //查找成功
printf("%lld\n", current);
break;
}
myQueue.push(current * 10);
myQueue.push(current * 10 + 1);//把邻居加入队列中
}
}
int main() {
int n;
//下面这个可以写成while(true){
while (scanf("%d", &n) != EOF) {
if (n == 0) {
break;
}
BFS(n);
}
return 0;
}
心得体会
这段代码体现的是广度优先遍历(BFS)算法。在函数 BFS 中,使用了一个队列 myQueue 来实现广度优先搜索。
广度优先遍历是一种遍历或搜索图或树的算法,它从起始节点开始,逐层地向外扩展,先访问当前层的所有节点,然后再访问下一层的节点。在代码中,初始状态为1,将其压入队列。然后,每次从队列中取出队首元素,检查是否满足条件(current % n == 0),如果满足,则输出结果并结束遍历。如果不满足条件,则将当前元素的倍数(current * 10 和 current * 10 + 1)压入队列,以便在下一层进行遍历。
由于广度优先搜索的特性,它会先遍历当前层的所有节点,然后再进入下一层。这是通过队列的先进先出(FIFO)特性来实现的。
9.2 深度优先搜索

last: 宽度优先搜索过程中,获得到一个状态后,立即扩展这个状态,并且保证早得到的状态优先得到扩展。因此,使用队列的先进先出特性来实现先得到的状态先扩展这一特性。
例 A Knight’s Journey
题目表述


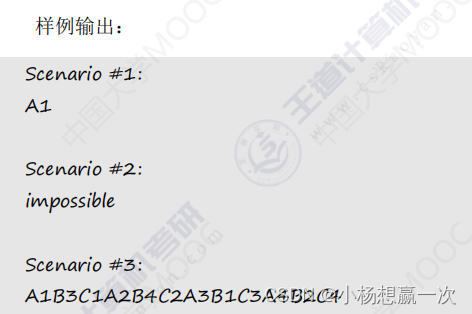
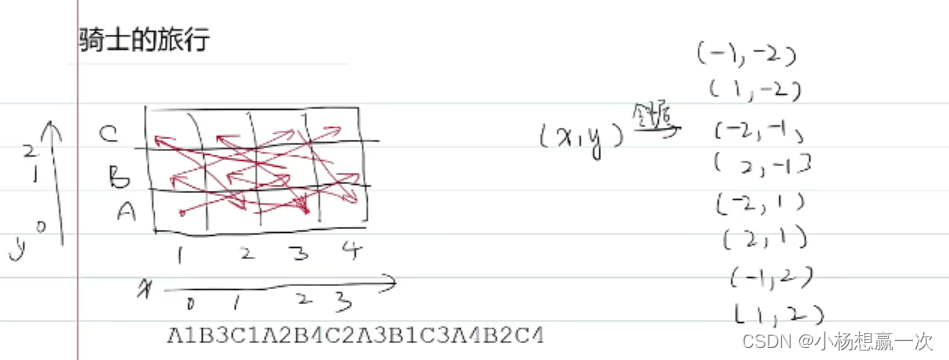
思路提示
2、检查扩展后的节点 (nx, ny) 是否满足以下条件:
- x 坐标小于 0 或大于等于 p(棋盘的行数)
- y 坐标小于 0 或大于等于 q(棋盘的列数)
(nx, ny)已经被访问过(在visit数组中对应位置为true)
如果上述任何一个条件满足,表示扩展后的节点是无效的或者已经被访问过,那么继续下一个循环迭代,不处理该节点。
3、direction[i][0] 表示 x 方向的偏移量,而 direction[i][1] 表示 y 方向的偏移量。这些偏移量代表了骑士在棋盘上移动的八个方向之一(上、下、左、右以及四个对角线方向)。
通过将偏移量 direction[i] 添加到当前节点的坐标 (x, y),我们得到了扩展后节点的坐标 (nx, ny)。这样,(nx, ny) 就成为了下一个可能的节点,我们将在接下来的搜索中对其进行处理。
4、使用了两个字符变量 col 和 row。
对于 col,我们将 ny 加上字符 'A',以将其转换为对应的列号。由于 'A' 的 ASCII 值为 65,因此当 ny 为 0 时,ny + 'A' 的结果为 'A',表示第一列;当 ny 为 1 时,ny + 'A' 的结果为 'B',表示第二列,以此类推。
对于 row,我们将 nx 加上字符 '1',以将其转换为对应的行号。由于 '1' 的 ASCII 值为 49,因此当 nx 为 0 时,nx + '1' 的结果为 '1',表示第一行;当 nx 为 1 时,nx + '1' 的结果为 '2',表示第二行,以此类推。
通过这样的转换,我们将扩展后的节点的坐标 (nx, ny) 转换为了对应的列号 col 和行号 row,以便在后续的操作中使用。这些列号和行号可以用于标识和表示节点在棋盘上的位置。
代码表示
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 30;
int p, q; // 棋盘参数
bool visit[MAXN][MAXN]; //标记矩阵判断某节点有没有被访问过
int direction[8][2] = {
{-1, -2}, {1, -2}, {-2, -1}, {2, -1}, {-2, 1}, {2, 1}, {-1, 2}, {1, 2}
};
//实现深度优先算法 接受当前节点(x, y)、当前步数 step、已经走过的路径 ans
bool DFS(int x, int y, int step, string ans) {
if (step == p * q) { // 这个已经走好到终点搜索成功
cout << ans << endl << endl;
return true;
} else {//试探邻居
//通过使用偏移量来计算扩展后的节点坐标 (nx, ny)
for (int i = 0; i < 8; ++i) { // 遍历邻居结点
// 扩展状态坐标
int nx = x + direction[i][0]; //x方向的偏移量
int ny = y + direction[i][1];//y方向的偏移量
// col 和 row 是用于表示当前节点编号
char col = ny + 'A'; //ny + 'A' 将 y 坐标转换为对应的字母编号
char row = nx + '1';// nx + '1' 将 x 坐标转换为对应的数字编号
if (nx < 0 || nx >= p || ny < 0 || ny >= q || visit[nx][ny]) {
continue;
}
//上条件都不满足,表示扩展后的节点是有效的且未被访问过将该节点标记为已访问
visit[nx][ny] = true; // 标记该点
//递归调用 DFS 函数继续搜索下一个扩展后节点
if (DFS(nx, ny, step + 1, ans + col + row)) {
return true;
}
visit[nx][ny] = false; // 取消标记
}
}
return false;
}
int main() {
int n;
cin >> n;
int caseNumber = 0;
while (n--) {
cin >> p >> q;
memset(visit, false, sizeof(visit));
cout << "Scenario #" << ++caseNumber << ":" << endl;
visit[0][0] = true; // 标记 A1 点
if (!DFS(0, 0, 1, "A1")) {
cout << "impossible" << endl << endl;
}
}
return 0;
}
心得体会
1、根据给定的起始节点 (x, y),开始深度优先搜索。
2、在每一步搜索中,对当前节点进行以下操作:
1)根据预定义的方向数组 direction,计算扩展后的节点的坐标 (nx, ny)。
2)将坐标转换为对应的列号和行号,分别存储在 col 和 row 中。
3)检查扩展后的节点 (nx, ny) 是否满足以下条件:
①(nx, ny) 已经被访问过(在 visit 数组中对应位置为 true)。
②y 坐标小于 0 或大于等于 q(棋盘的列数)。
③ x 坐标小于 0 或大于等于 p(棋盘的行数)。
④ 如果任何条件满足,则跳过当前节点,继续下一次循环迭代。
⑤ 否则,将 (nx, ny) 标记为已访问,并进行递归调用 DFS 函数:
a、如果递归调用返回 false,表示在该节点的搜索路径下没有找到满足条件的路径,将该节点的标记取消,并继续尝试其他邻居节点。
b、如果递归调用返回 true,表示找到了满足条件的路径,直接返回 true。
c、将扩展后节点的坐标 (nx, ny)、步数 step + 1 和路径 ans + col + row 作为参数传递。
3、如果在所有的邻居节点中都没有找到满足条件的路径,那么返回 false,表示无法找到完整路径。
整体思路:通过深度优先搜索算法,在棋盘上搜索从起始节点开始的路径。在搜索过程中,通过递归调用不断扩展当前节点,并检查扩展后的节点是否满足条件。如果找到了满足条件的路径,立即返回 true,否则继续搜索其他可能的路径。如果所有的路径都被搜索完毕,仍然没有找到满足条件的路径,返回 false。
广度和深度的区别:
广度优先搜索(BFS)和深度优先搜索(DFS)是两种常见的图搜索算法,它们在搜索顺序、空间复杂度和搜索结果等方面有一些区别。
1、搜索顺序:
BFS:从起始节点开始,逐层地扩展搜索,先访问离起始节点最近的节点,再逐渐向外扩展到离起始节点更远的节点。
DFS:从起始节点开始,沿着路径一直向下搜索,直到达到最深的节点,然后回溯到上一个节点,继续搜索其他路径。
2、空间复杂度:
BFS:需要使用队列来存储待访问的节点,以及标记已访问的节点。在最坏情况下,当图为树状结构时,BFS 的空间复杂度为 O(V),其中 V 是图中节点的数量。
DFS:通常使用递归栈来存储函数调用的信息。在最坏情况下,当图为链状结构时,DFS 的空间复杂度为 O(V),其中 V 是图中节点的数量。然而,在实际应用中,DFS 的空间复杂度往往较低,因为它只需要存储一条路径上的节点。
3、搜索结果:
BFS:保证找到的路径是离起始节点最近的路径,因此在无权图,BFS 通常用于寻找最短路径。
DFS:不能保证找到的路径是最短路径,因为它会优先探索深度较大的路径。
4、应用场景:
BFS:适用于需要找到最短路径或层次遍历的问题,如迷宫最短路径、社交网络中的关系查找等。DFS:适用于需要遍历整个图或搜索特定路径的问题,如图的连通性判断、拓扑排序、深度优先遍历等。
具体实例理解:
迷宫问题:
假设你被困在一个迷宫中,你需要找到一条从起点到终点的路径。在这种情况下,BFS 和 DFS 的不同表现如下:
BFS:你会选择先尝试从起点开始,逐层地向外扩展搜索。你先探索离起点最近的位置,并在每一层继续探索与当前位置相邻的位置,直到找到终点或者遍历完整个迷宫。BFS 可以保证你找到的路径是最短路径。
DFS:你会选择从起点开始,沿着一条路径一直深入迷宫,直到遇到死胡同或者找到终点。如果遇到死胡同,你会回溯到上一个节点,继续搜索其他路径。DFS 不一定能找到最短路径,但它可以帮助你遍历整个迷宫,找到其中的一条路径。
社交网络中的关系查找:
假设你在一个社交网络中,想要查找与你有共同朋友的人。在这种情况下,BFS 和 DFS 的不同表现如下:
BFS:你会选择从自己开始,首先查找与你直接相连的人(一度关系),然后查找与这些人直接相连的人(二度关系),依次类推。BFS 可以帮助你逐层地扩展查找,找到与你有共同朋友的人,并且先找到的人与你的关系更近。
DFS:你会选择从自己开始,深入其中一位朋友的朋友(二度关系),然后继续深入这个人的朋友(三度关系),直到找到与你有共同朋友的人或者遍历完整个网络。DFS 可以帮助你搜索到可能较远的关系,但无法保证先找到的人与你的关系更近。
蓝桥杯真题
[蓝桥杯 2021 国 BC] 大写
题目描述
给定一个只包含大写字母和小写字母的字符串,请将其中所有的小写字母转换成大写字母后将字符串输出。
输入格式:输入一行包含一个字符串。
输出格式:输出转换成大写后的字符串。

代码表示
#include <bits/stdc++.h>
using namespace std;
int main() {
string arr;
cin >> arr;
for (int i = 0; i < arr.size(); ++i) {
if (arr[i] >= 'a' && arr[i] <= 'z') {
cout << char(arr[i] - 'a' + 'A');
} else {
cout << arr[i];
}
}
return 0;
}心得体会
1、注意用到字符串里面字符串的大小使用arr.size()不要忘记加括号
2、arr[i] - 'a' 时,我们实际上是计算 arr[i] 相对于小写字母 a 的偏移量。假设 arr[i] 对应小写字母 b,那么 arr[i] - 'a' 的结果就是 1,因为小写字母 b 在小写字母表中的位置相对于 a 往后偏移了一个位置。再加上 'A' 的ASCII码值,就可以将偏移量转换为大写字母的ASCII码值。
[蓝桥杯 2020 省 B1] 整除序列
题目描述
有一个序列,序列的第一个数是 n,后面的每个数是前一个数整除 2,请输出这个序列中值为正数的项。
输入格式 输入一行包含一个整数 n。
输出格式 输出一行,包含多个整数,相邻的整数之间用一个空格分隔,表示答案。

代码表示
#include <bits/stdc++.h>
using namespace std;
int main() {
long long n;
cin>>n;
while(n){
cout<<n<<" ";
n=n/2;
}
return 0;
}心得体会
1、注意要使用long long类型,有一天我也会因为这个出错!!

2、注意代码得逻辑就是要先输出再进行算数。
[蓝桥杯 2020 省 AB3] 日期识别
题目描述
小蓝要处理非常多的数据, 其中有一些数据是日期。在小蓝处理的日期中有两种常用的形式:英文形式和数字形式。英文形式采用每个月的英文的前三个字母作为月份标识,后面跟两位数字表示日期,月份标识第一个字母大写,后两个字母小写, 日期小于 10 时要补前导0。1月到 12 月英文的前三个字母分别是 Jan、Feb、Mar、Apr、May、Jun、Jul、Aug、Sep、Oct、Nov、Dec。
数字形式直接用两个整数表达,中间用一个空格分隔,两个整数都不写前导 0。其中月份用 1 至 12 分别表示 1 月到 12 月。输入一个日期的英文形式, 请输出它的数字形式。
输入格式 输入一个日期的英文形式。
输出格式 输出一行包含两个整数,分别表示日期的月和日。

代码表示
#include <bits/stdc++.h>
using namespace std;
string a[12]={"Jan","Feb","Mar","Apr","May","Jun","Jul","Aug","Sep","Oct","Nov","Dec"};
int main()
{
int m=0,d=0;
//定义了两个字符串变量st和month
string st,month="";
cin>>st;//输入日期字符串
month=st.substr(0,3);//提取月份的英文缩写
for(int i=0;i<12;i++){
if(month==a[i]){
//数组下标(0~11)转换为实际的月份(1~12)
m=i+1;
break;
}
}
d=int(st[3]-'0')*10+int(st[4]-'0');//第四位和第五位字符转换为对应的数字
cout<<m<<' '<<d;
}心得体会
1、st.substr(0,3)表示从字符串st的起始位置开始(即索引0),提取长度为3的子字符串。C++标准库中的string类提供的成员函数substr,用于从字符串中提取子字符串。
2、st[3] 和 st[4]:st是一个字符串变量,通过下标索引可以访问字符串中的特定字符。st[3]表示访问字符串st中索引为3的字符,即日期的十位数字;st[4]表示访问索引为4的字符,即日期的个位数字。
int(st[3]-48) 和 int(st[4]-48):ASCII码中数字0到9的顺序是连续的,'0'对应的ASCII码是48,因此通过将字符减去48后得到的就是对应的数字值。这里将st[3]和st[4]转换为对应的数字。
3、d=int(st[3]-'0')*10+int(st[4]-'0');在这段代码中我们可以把 ‘0’ 写成 48同样也可以。由于48就是0的ASCII码值大小。
























 1827
1827

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








