供应链-补货模型

上一篇文章，介绍了安全库存，在本片文章则讲解供应链-补货模型。

补货模型分有多种类型，大致上可以分为两类，定期补货模型和定量补货模型。

一、定量补货模型（R, S）

1. 模型逻辑

• 触发条件：当库存水平降至再订货点（Reorder Point, R）时，立即触发补货。

• 

• 补货量：一般情况下，每次补货量为经济订单量（EOQ），也可以根据经验设定补货量和补货点，下述为以EOQ模型为例设计补货点与补货量的过程。

• 公式：

  • 再订货点 R = 提前期内的平均需求 × 提前期 + 安全库存

R=D×L+SS

             补货量 Q = EOQ（经济订单量，会在文章结尾对此模型讲解）

其中，D：年需求量，S：单次订货成本，H：单位库存持有成本。

2. 适用产品

• 高价值物品：如电子元器件、医疗器械。

• 需求稳定：需求波动较小，可预测性强的产品。

• 缺货成本高：需严格控制缺货风险（如关键备件）。

3. 特点与优势

• 实时监控：持续跟踪库存水平，响应迅速。

• 低缺货风险：通过安全库存应对需求波动。

• 成本优化：通过 EOQ 最小化总成本（订货成本 + 持有成本）。

4. 输入数据

• 需求数据：历史需求均值与标准差。

• 提前期（L）：从下单到到货的时间。

• 成本参数：订货成本（S）、持有成本（H）、缺货成本（若考虑服务水平）。

5. 输出数据

• 再订货点（R）。

• 经济补货量（Q）。

• 安全库存（SS）水平。

6. 示例

• 场景：某汽车零部件经销商销售某型号轴承，需求稳定。

• 参数：

  • 日均需求 D=10个，提前期 L=5天。

  • 年需求量 Dannual=3650，订货成本 S=100元/次，持有成本 H=2元/个/年。

  • 目标服务水平 95%（对应安全系数 Z=1.65Z=1.65），需求标准差 σ=2 个/天。

• 计算：

  • 安全库存 SS==1.65×2×5≈7.4 个

  • 再订货点 R=D×L+SS=10×5+7.4=57.4→ 58 个(取整)。

  • 补货量 Q=2×3650×1002≈604个。

二、定期补货模型（T, S）

1. 模型逻辑

• 触发条件：每隔固定周期 T 检查库存，补货至目标库存水平 S。

• 

• 补货量：补货量 = 目标库存 S - 当前库存 - 在途库存。

• 公式：

  • 目标库存 S = 覆盖期内的平均需求 × (T + L) + 安全库存
    S=D×(T+L)+SS

2. 适用产品

• 需求波动大：如季节性商品（服装、节日礼品）。

• 多品类集中采购：如超市杂货，可降低管理复杂度。

• 供应商协同：固定周期便于与供应商协调送货。

3. 特点与优势

• 管理简单：固定时间检查，减少监控成本。

• 批量采购折扣：适合集中采购场景。

• 灵活应对需求波动：通过调整目标库存 S 适应变化。

4. 输入数据

• 检查周期（T）：如每周、每月。

• 提前期（L）从下单到到货的时间。

• 需求分布：覆盖期（T + L）内的需求均值和标准差。

5. 输出数据

• 目标库存水平（S）。

• 补货周期（T）。

• 每次补货量（动态调整）。

6. 示例

• 场景：某快消品零售商销售季节性饮料，需求波动较大。

• 参数：

  • 检查周期 T=7 天，提前期 L=3 天。

  • 覆盖期需求均值 D=100个/周，标准差σ=20 个。

  • 目标服务水平 90%（Z=1.28）。

• 计算：

  • 安全库存 SS=个。

  • 目标库存 S=D×(T+L)+SS=100×10+81=1081个。

  • 若当前库存为 200 个，在途库存为 150 个，则补货量 = 1081 - 200 - 150 = 731 个。

三、对比总结

维度	定量补货模型（R, S）	定期补货模型（T, S）
触发机制	库存水平降至 R 时触发	固定周期 T 触发
补货量	固定（EOQ）	动态（补至 S）
库存监控成本	高（需实时监控）	低（周期检查）
缺货风险	低（实时响应）	较高（依赖周期设置）
适用场景	高价值、需求稳定、缺货成本高	需求波动大、多品类、供应商协同
成本优化	通过 EOQ 最小化总成本	通过批量采购降低订货成本

四、选择建议

1. 定量模型（R, S）：

   • 适用于精细化管理场景，如关键备件、医疗物资。

   • 需确保需求预测准确性和实时库存监控能力。

2. 定期模型（T, S）：

   • 适用于需求波动大或多品类集中采购场景，如零售、快消品。

   • 需合理设置检查周期 T 和目标库存 S，平衡服务水平与库存成本。

 通过以上分析，读者可清晰理解两种模型的差异及适用场景，为实际业务中的补货策略选择提供理论依据。

彩蛋

能看到这里的朋友，相信大家对于补货模型已经有了了解，现在为大家讲解一下经济订过货批量模型（EOQ）。

1. EOQ模型的原理

经济订货批量（EOQ） 是一种库存管理工具，用于确定企业每次采购货物的最佳数量。其核心原理是在订货成本和持有成本之间找到平衡，使得总成本最小化。

订货成本 是指企业每次下订单所产生的费用，包括采购部门的运营成本、与供应商沟通协商的成本、运输成本等。这些成本与订货次数直接相关，每次订货都会产生固定的费用，所以订货次数越多，订货成本越高。

持有成本 是指企业持有库存所产生的费用，包括仓储成本（如仓库租金、设备折旧、仓库管理人员工资等）、资金占用成本（库存占用资金的利息等）、库存损耗成本（如货物变质、过期等）。持有成本与库存水平直接相关，库存数量越多，持有成本越高。

总成本（TC） 是订货成本和持有成本之和。在年度总需求量一定的情况下，订货量和订货次数的关系如下：

• 每次采购得越多，采购次数就越少，采购成本就越低，但持有成本就高。

• 每次采购得越少，采购次数就越多，采购成本就越高，但持有成本就低。

 数学推导过程如下

其中，Q * 为经济订货批量；C为单次订货成本；R为年总需求量；P ：货物单价 (元／件) ；F ：每件存货的年保管费用占其价值的百分比；H=PF:单位产品的库存成本，即每件存货的年平均库存保管费用(元／件·年) 。

示意图如下图所示

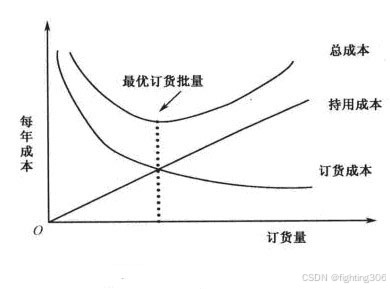
 总结，经济订货批量模型就是帮你找到最小的总成本。