《信号与系统》第三章 傅里叶变换

傅里叶变换对信号的重要性应该不用我多说了吧！

这章内容较多，大家务必好好看，概念要理解，计算要会，弄懂每一道例题自己动笔算，要不死翘翘，哈哈哈，大家加油！

目录

3.1 周期信号的频谱分析

一、正交函数集

二、三角函数形式的傅里叶级数展开式与单边频谱

1、狄里克利条件

2、傅里叶级数的其他形式

3、周期信号的频谱

4、 频带宽度

 三、指数函数形式的傅里叶级数展开式与双边频谱

 1、指数形式傅里叶级数

 2、二种形式傅里叶级数的关系

 四、函数对称性与傅里叶级数的关系

3.2 典型周期信号的傅里叶级数

3.3 非周期信号的频谱

3.4 典型非周期信号的傅里叶变换

3.5傅里叶变换的性质

一、线性（叠加性）

二、时频对偶性

三、展缩（尺度变换）特性

四、时移特性

五、频移特性（调制）与调幅波

六、微分特性

七、奇偶虚实性

八、反褶与共轭特性

九、卷积定理

1、时域卷积，频域相乘

2、时域相乘，频域卷积×1/2

3、时域积分性质

4、微分和积分性质的不对称性

5、傅氏变换计算题

3.6 周期信号的傅里叶变换

3.7 抽样信号的傅里叶变换和抽样定理

1、抽样即信号时域相乘

2、理想抽样

3、自然（脉冲）抽样

4、抽样定理（考！！！）

---

3.1 周期信号的频谱分析

一、正交函数集

一个区间上的任意能量有限信号可以在正交函数集中分解，称为正交分解，其误差函数利用最小均方误差准则来确定待定系数。

二、三角函数形式的傅里叶级数展开式与单边频谱

1、狄里克利条件

周期信号满足只有有限个极值点、有限个一类间断点、绝对可积三个条件，才可展开为三角函数形式的傅里叶级数。

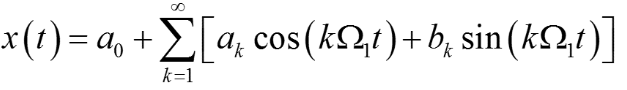
k=1:基波分量      k≥2 :k次谐波分量

2、傅里叶级数的其他形式

 3、周期信号的频谱

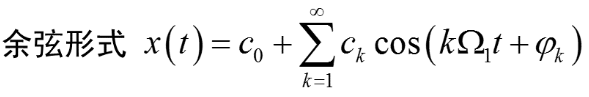
 包络线连接各谱线顶点，谱线只出现在离散频率点，即周期信号频谱具有谐波性、离散性、收敛性。

 

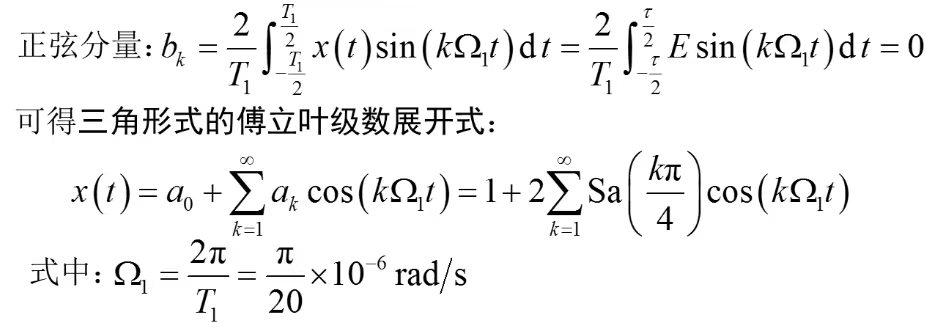
4、 频带宽度

 三、指数函数形式的傅里叶级数展开式与双边频谱

1、指数形式傅里叶级数

 2、二种形式傅里叶级数的关系

 重点例题（五星）！！！

 

 

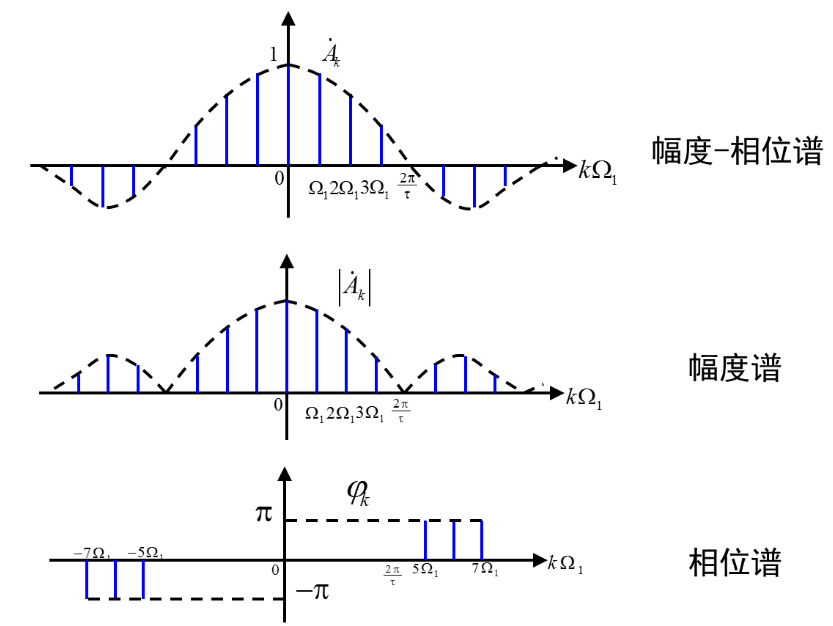
四、函数对称性与傅里叶级数的关系

3.2 典型周期信号的傅里叶级数

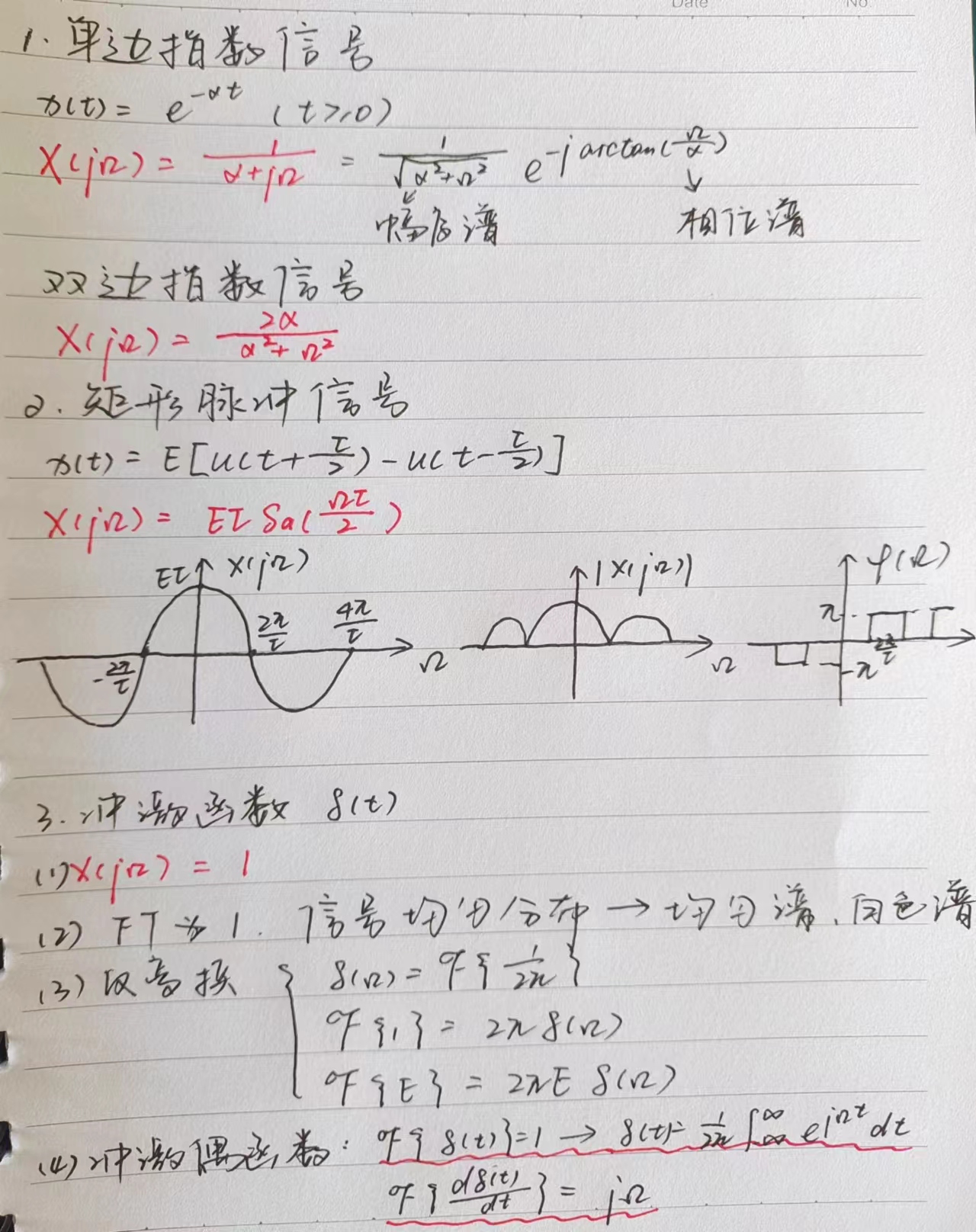
周期矩形脉冲信号

 

3.3 非周期信号的频谱

3.4 典型非周期信号的傅里叶变换

 

 

3.5傅里叶变换的性质

一、线性（叠加性）

满足叠加定理：相加信号的频谱等于各个单独信号的频谱之和

二、时频对偶性

 三、展缩（尺度变换）特性

 

 

 结论： 0<a<1 时域扩展，频域压缩

             a>1 时域压缩，频域扩展

             a=-1 时域反褶，频域反褶

四、时移特性

 

 

 

 

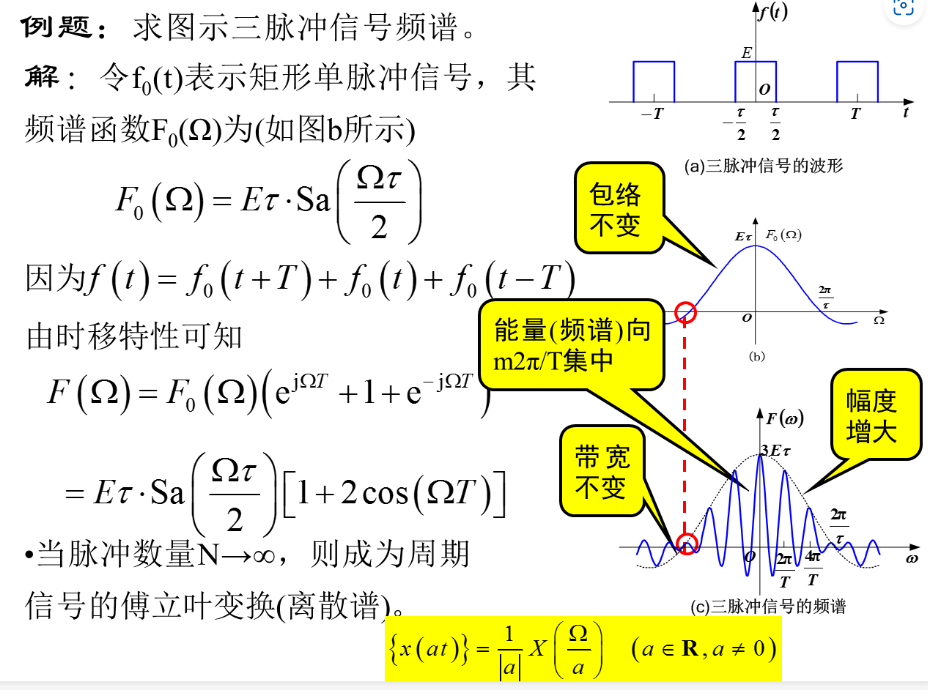
 五、频移特性（调制）与调幅波

 频谱搬移原理

 六、微分特性

 

 

 

 七、奇偶虚实性

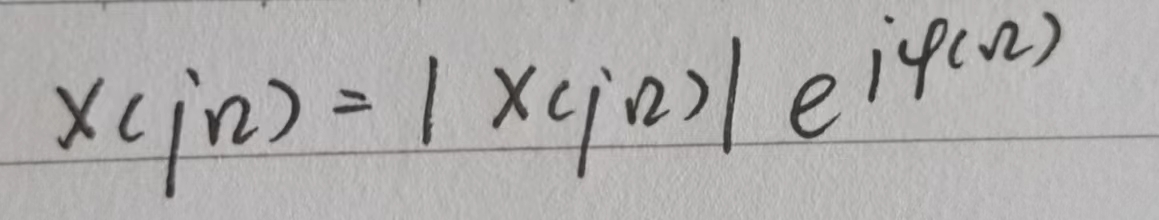
 八、反褶与共轭特性

 

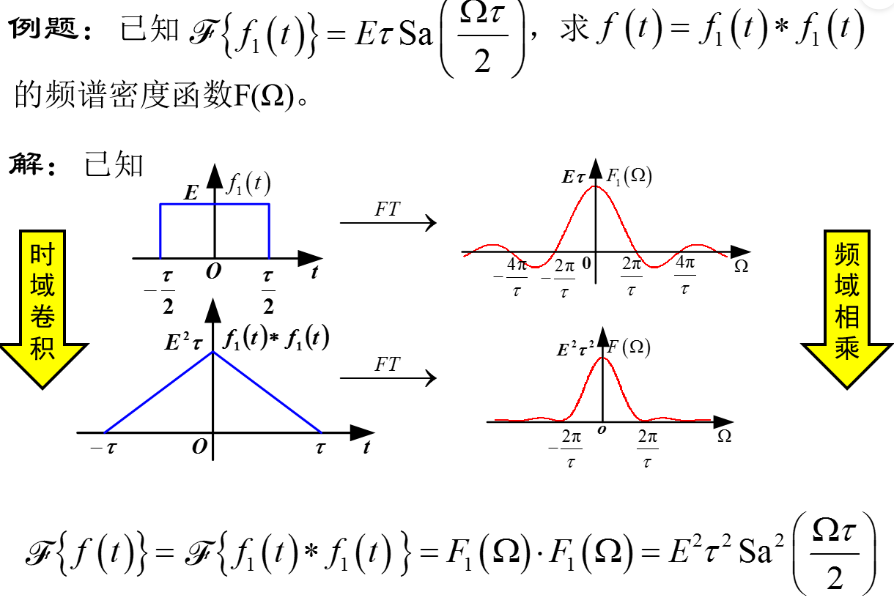
 九、卷积定理

1、时域卷积，频域相乘

2、时域相乘，频域卷积×1/2

 

 3、时域积分性质

 4、微分和积分性质的不对称性

 

 

 

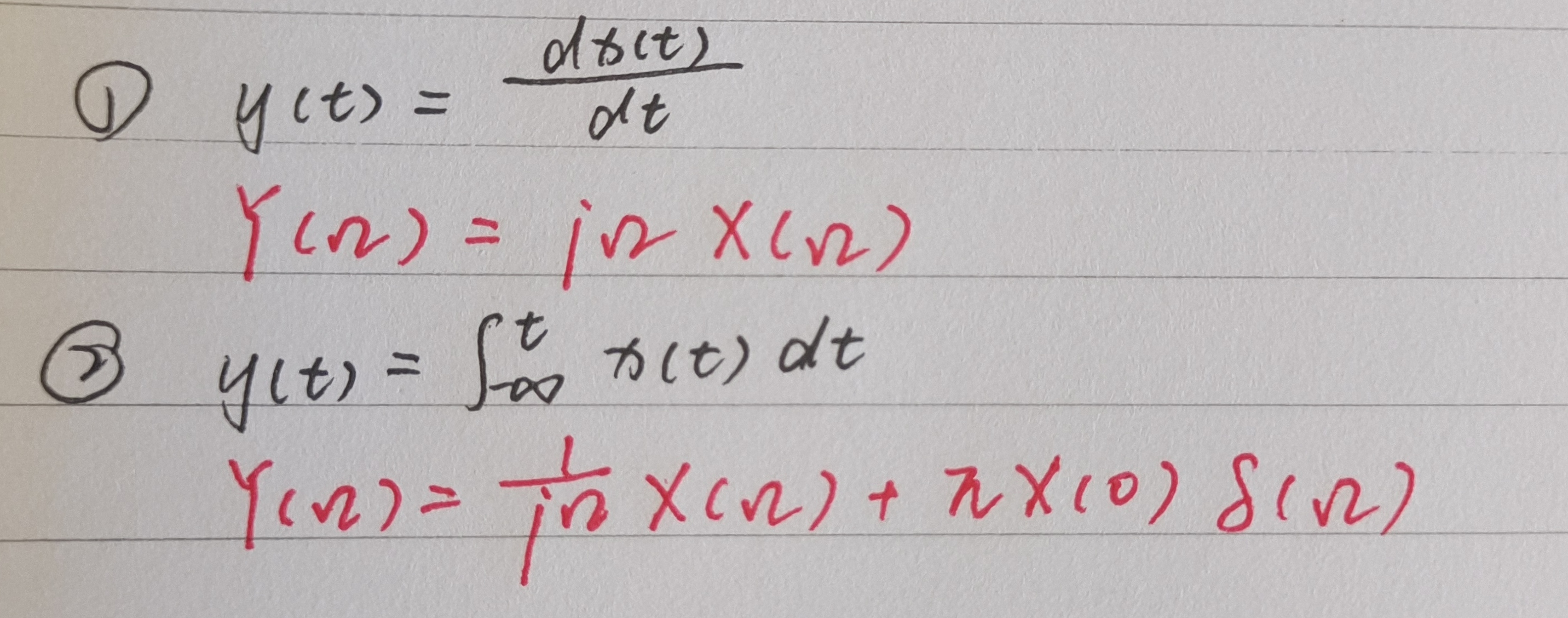
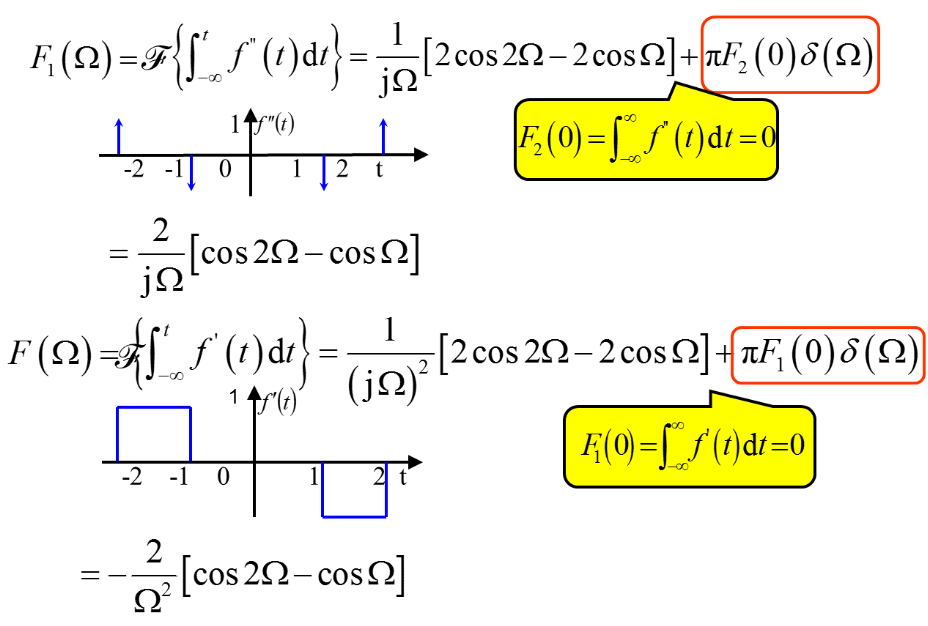
 5、傅氏变换计算题

 

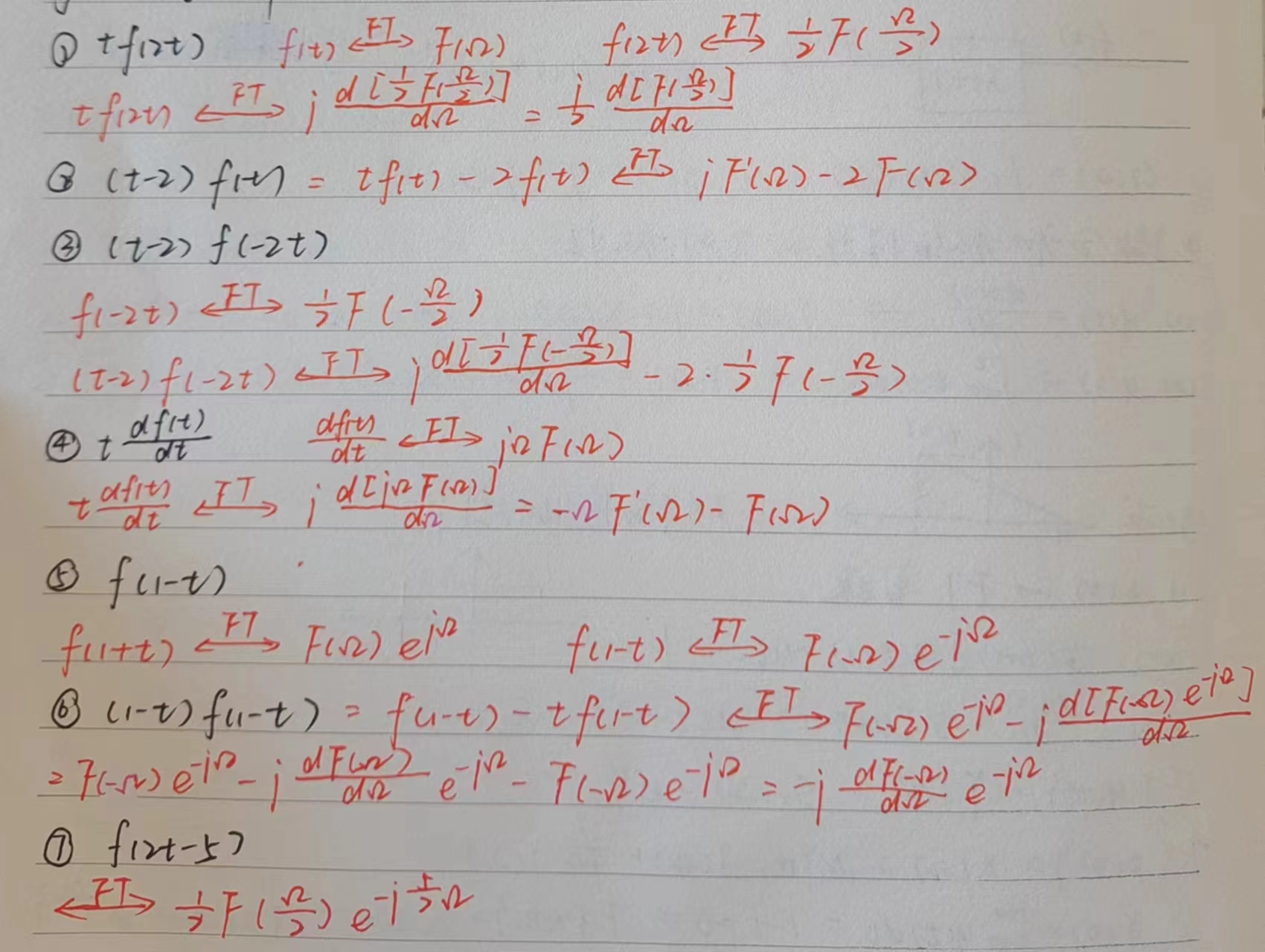
3.6 周期信号的傅里叶变换

 

3.7 抽样信号的傅里叶变换和抽样定理

1、抽样即信号时域相乘

 2、理想抽样

抽样脉冲序列为单位冲激序列时，称为理想抽样

 3、自然（脉冲）抽样

抽样脉冲序列为周期矩形脉冲

4、抽样定理（考！！！）

 5、由抽样信号恢复原信号：通理想低通滤波器