空间解析几何：圆柱面一般式方程的推导——已知中轴线和半径

        本文主要针对在已知中轴线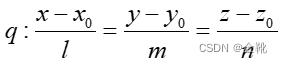和半径r的情况下（其中为中轴线上的已知一点）如何来求解圆柱面方程做出详细解答。

 1.圆柱面模型的建立：

 

Step 1：假设点P 为待求圆柱面上的任意一点，由于点P到直线q的垂直距离PM为r，即，其中，点M为直线q上一点，。

Step 2：由欧式距离公式和直线对称式方程的原理可得

 由的向量式可得：

 其中为直线的方向向量。

 Step 3：由上图几何关系可知

 又因为，

所以得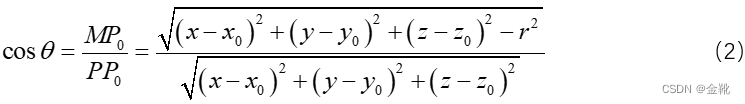

 Step 4：由于式（1）和式（2）用不同方法求，

所以有式（1）=式（2），即如下等式：

 从而得到该待求圆柱面的一般方程式：

 

下面以2021年全国大学生数学建模竞赛A题第二问为例。

       若要求出在该抛物面斜上方即300m口径上方所有的点，可以构造一个以300m口径为准线，平行于直线CS为母线的圆柱体，从而利用圆柱体方程内部不等式的关系求出所有主索节点中以直线CS为投影方向，投影在该300m口径中的主索节点。

2.圆柱面模型的求解：

     由题已知，当待观测天体𝑆位于𝛼 = 36.795°, 𝛽 = 78.169时，其理想抛物面的方程为：

       

明显可知该抛物面的轴线不平行于任何一个坐标轴即该抛物面是斜置在三维空间坐标系中。

可以构造一个以抛物面中轴线CS为轴线，半径为150m的圆柱面。

 本题中

 代入上述模型中，可得：

 所以可分别求得的向量式与几何关系式

 其中𝛼 = 36.795°, 𝛽 = 78.169°，r=150m，

 所以可得圆柱面方程：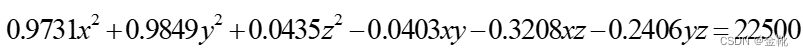

 且三维空间坐标系内任意一点在圆柱面内外的关系如下：