2.7 计算图
一个神经网络的计算都是按前向和反向传播过程实现的。首先前向传播计算出神经网络的输出,再进行反向传播用于计算对应的导数,这些导数可以用于更新参数;

实际上,在数学上是不太规范的,为了进一步说明,用问答来做思考:
 是
是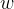 和
和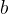 的函数吗?
的函数吗?
不是呀。可是一个
维的列向量,什么时候见过有函数以列向量作为变量的;
所以一般是记为:
然后说,是
的函数,真正有数学意义的是以下等式:
其中,,
,
而编程时,仍然可以编为这是因为能自动执行多行对应计算(向量化):
将最后一项记为:
则,证毕;效果就是一行代码执行了
个式子;
2.9 logistic回归中的梯度下降法(单样本)
现在引入符号规定:
因为只考虑单样本,所以不必加上标,并且为了简化例子,假设
是二维的,
也是二维的,即

现在要计算所有导数,根据计算图可以知道要求;注意,一般不对输入特征求偏导,因为在监督学习当中,将输入特征
视作已知不变量;
把计算的导数,
,
应用到
,
,
当中就可以了;在后面,会看到计算机是如何实现这一过程的,剧透一下就是前向传播中会储存
并在后向传播中用到,后向传播会逐层传播
并输出导数
等,最后执行梯度下降;
值得注意的是即使扩展到多维,也能够将以上式子简写为两行代码:
前者已经证明过,后者的证明:
注意,这里都是实数,一般
与
保持一致的矩阵形式,
与
保持一致的矩阵形式,所以
都是实数。
2.10 m个样本的梯度下降
为了不失一般性、清楚地加以证明,先定义如下:
输入特征是多维的,维数记为,这意味着所有样本的输入即
都是
维列向量,同理
也是
维列向量;并记:
难点在于研究对象由变成了
;
我们使用梯度下降法的式子还是不变:,
,……,
,
,所求的导数还是
,但是含义已经发生了改变:
也就是说以为例,不过是一个样本均值,真正要求的是每个样本中损失函数对
的偏导数;
那么,在样本1中, 是什么呢?
是什么呢?
这就是我们在2.9对单样本已经证明过的公式,当时写的是这样的:
现在给它加上一个上标,表示这是来自样本1的数据:
这一步是最难理解的,多想一下,然后注意每一个都是带标签的项,除了对求导;
同理,可以得到样本2,样本3,……,样本m的式子:
将这个式子总结成一般化公式:
同理,对的导数也是如此推导,简洁起见在
公式上改一下下标就可以了:
而对于的导数推导简直一模一样,甚至更简单:
到此,大致总结一下:
那么,式子中未知的只有 了,如何求呢?
了,如何求呢?
其实在2.9节也早就求过了,当时是单样本下写成这样的:
现在只不过要带上标了,以第个样本为例,扩展到
所有样本中去:
如何进行编程?
首先先从最容易的for loop开始构思,后续再用向量化把可以去掉的for loop去掉;
一开始,要对和
进行初始化,可以初始化为0;
然后我们先从这个式子出发,可以用for loop把
全部加到
这个变量里,加完最后再将
除以
即可;然后如法炮制到
和
中;
最后就可以进行一次梯度下降了;如果要多次梯度下降,只能在所有的代码最外围再添加一个for loop,而且这个for loop是无法省略的;
版本1:
对中间的等用for loop循环代替,并做好各处标记方便向量化,有:
版本2:
深度学习中不用显式for loop是非常重要的,会极快地提升算法的速度。





















 5339
5339

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








