最优化学习笔记：无约束优化算法（2）

6.2 梯度类算法

本节介绍梯度类算法，其本质是仅仅使用函数的一阶导数信息选取下降方向 $d^k$。这其中最基本的算法是梯度下降法，即直接选择负梯度作为下降方向 $d^k$。梯度下降法的方向选取非常直观，实际应用范围非常广，因此它在优化算法中的地位可相当于高斯消元法在线性方程组算法中的地位。此外也会介绍 BB 方法。该方法作为一种梯度法的变形，虽然理论性质目前仍不完整，但由于它有优秀的数值表现，也是在实际应用中使用较多的一种算法。

6.2.1 梯度下降法

对于光滑函数 $f(x)$，在迭代点 $x^k$ 处，需要选择一个较为合理的 $d^k$ 作为下降方向。注意到 $\varphi (\alpha )=f(x^k+\alpha d^k)$ 有泰勒展开
$$\varphi (\alpha )=f(x^k)+\alpha \nabla f(x^k{)}^{\mathrm{T}}{d}^k+\mathcal{O}({\alpha }^2\Vert d^k{\Vert }^2)$$

根据柯西不等式，当 $\alpha$ 足够小时，取 $d^k=-\nabla f(x^k)$ 会使得函数下降最快。因此梯度法就是选取 $d^k=-\nabla f(x^k)$ 的算法，它的迭代格式为
$$x^{k+1}=x^k-{\alpha }_k\nabla f(x^k)(\mathrm{6.2.1})$$

步长 ${\alpha }_k$ 的选取可依赖于线搜索算法，也可直接选取固定的 ${\alpha }_k$。

为了直观地理解梯度法的迭代过程，以二次函数为例来展示该过程。

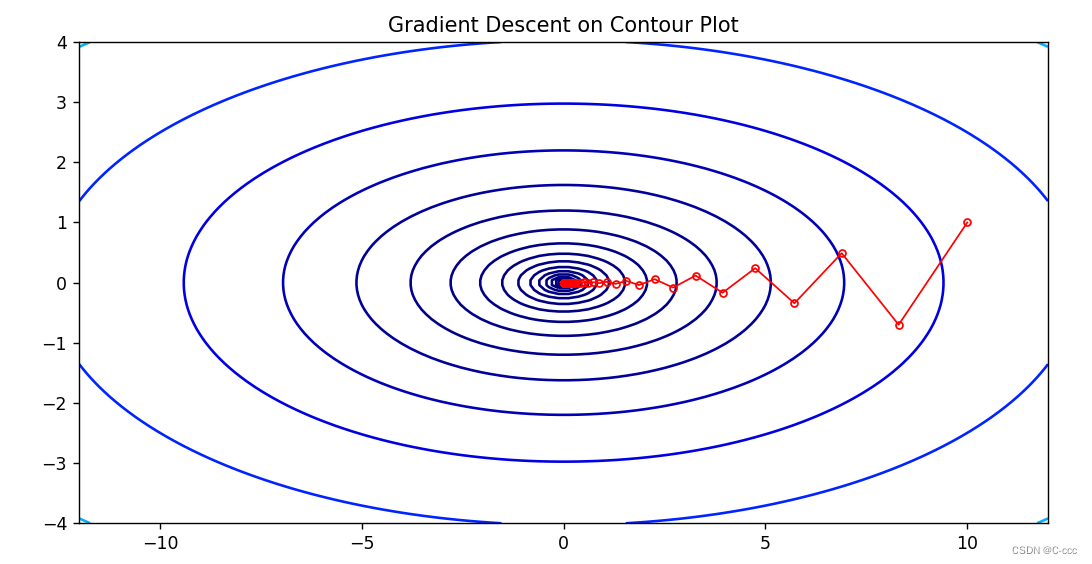
例 6.2 (二次函数的梯度法) 设二次函数 $f(x,y)=x^2+10y^2$, 初始点 $(x^0,y^0)$ 取为 (10,1)，取固定步长 ${\alpha }_k=0.085$。使用梯度法 $x^{k+1}=x^k-{\alpha }_k\nabla f(x^k)$ 进行 15 次迭代，结果下图所示。

# 例 6.2
import numpy as np
import matplotlib.pyplot as plt
# 定义二次函数
def f(x):
    return x[0]**2 + 10*x[1]**2
# 定义梯度计算函数
def grad_f(x):
    return np.array([2*x[0], 20*x[1]])
# 定义梯度下降算法
def gradient_descent(x, alpha, iter = 300, tol = 1e-6):
    x_history = [x]
    k = 0
    while k < iter:
        x = x - alpha * grad_f(x)
        x_history.append(x)
        k = k + 1
        if np.linalg.norm(grad_f(x)) < tol:
            break
    return x_history, k
# 设置初始点和迭代参数
x0 = np.array([10, 1])
alpha = 0.085
# 进行梯度下降迭代
gd_history, k = gradient_descent(x0, alpha)
print("Optimal solution:", gd_history[-1])
'''Optimal solution: [ 4.32619814e-07 -8.01533432e-15]'''
print("迭代次数：", k)
'''迭代次数： 91'''
# 定义网格点
x = np.linspace(-12, 12, 100)
y = np.linspace(-4, 4, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2  # 定义目标函数
# 绘制等高线图
plt.figure(figsize=(10, 5))
plt.contour(X, Y, Z, levels=np.logspace(-2, 3, 20), cmap='jet')  # levels 参数控制等高线的密集程度
plt.plot([x[0] for x in gd_history], [x[1] for x in gd_history], marker='o',markersize=4, linewidth=1, color = 'red', markerfacecolor='none', label='Gradient Descent')
plt.title('Gradient Descent on Contour Plot')
plt.show()

定理 6.2 (二次函数的收敛定理) 考虑正定二次函数
$$f(x)=\frac{1}{2}{x}^{\mathrm{T}}Ax-b^{\mathrm{T}}x$$

其最优值点为 $x^{\ast }$。若使用梯度法 (6.2.1) 并选取 ${\alpha }_k$ 为精确线搜索步长，即
$${\alpha }_k=\frac{\Vert \nabla f(x^k){\Vert }^2}{\nabla f(x^k{)}^{\text{T}}A\nabla f(x^k)}(\mathrm{6.2.2})$$

则梯度法关于迭代点列 { x k } \{x^k\} {xk} 是 Q-线性收敛的，即
$$\Vert x^{k+1}-x^{\ast }{\Vert }_A^2⩽{\left(\frac{{\lambda }_1-{\lambda }_n}{{\lambda }_1+{\lambda }_n}\right)}^2\Vert x^k-x^{\ast }{\Vert }_A^2$$

其中 ${\lambda }_1,{\lambda }_n$ 分别为 $A$ 的最大、最小特征值，$\Vert x{\Vert }_A\stackrel{\mathrm{def}}{=}\sqrt{x^{\mathrm{T}}Ax}$ 为由正定矩阵 $A$ 诱导的范数。

回顾 Q-收敛速度
以点列的 Q-收敛速度 (Q 的含义为“quotient”) 为例 (函数值的 Q-收敛速度可以类似地定义)。设 { x k } \{x^k\} {xk} 为算法产生的迭代点列且收敛于 $x^{\ast }$，若对充分大的 $k$ 有
$$\frac{\Vert x^{k+1}-x^{\ast }\Vert }{\Vert x^k-x^{\ast }\Vert }⩽a,a\in (0,1),$$

则称算法 (点列) 是 Q-线性收敛的；若满足
$$\underset{k\to \infty }{\lim }\frac{\Vert x^{k+1}-x^{\ast }\Vert }{\Vert x^k-x^{\ast }\Vert }=0,$$

称算法(点列)是 Q-超线性收敛的；若满足
$$\underset{k\to \infty }{\lim }\frac{\Vert x^{k+1}-x^{\ast }\Vert }{x^k-x^{\ast }}=1,$$

称算法 (点列) 是 Q-次线性收敛的. 若对充分大的 $k$ 满足
$$\frac{\Vert x^{k+1}-x^{\ast }\Vert }{\Vert x^k-x^{\ast }{\Vert }^2}⩽a,a>0,$$

则称算法 (点列) 是 Q-二次收敛的. 类似地，也可定义更一般的 Q-r 次收敛（$r>1$）．

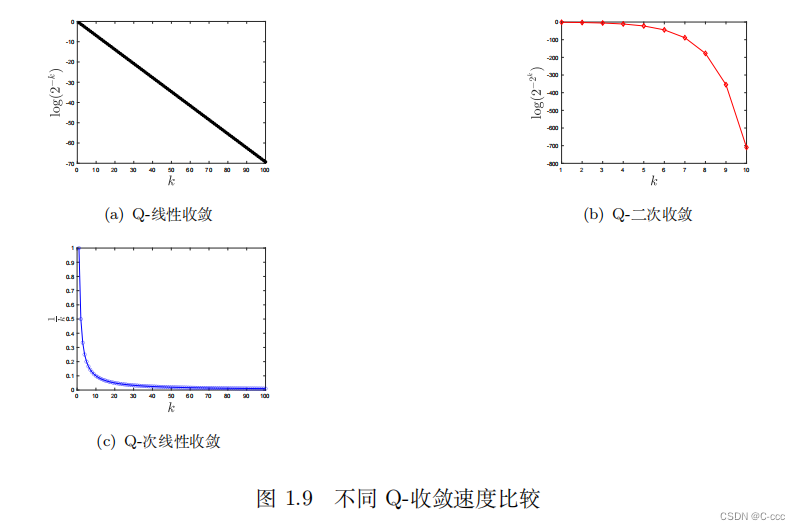
点列 { 2 − k } \{2^{-k}\} {2−k} 是 Q-线性收敛的，点列 { 2 − 2 k } \{2^{-2^k}\} {2−2k} 是 Q-二次收敛的 (也是 Q-超线性收敛的), 点列 { 1 k } \{\frac1k\} {k1​} 是 Q-次线性收敛的. 一般来说，具有 Q-超线性收敛速度和 Q-二次收敛速度的算法是收敛较快的.

R-收敛速度
以点列的 R-收敛速度 (R 的含义为“root”) 为例，设 { x k } \{x^k\} {xk} 为算法产生的迭代点列且收敛于 $x^{\ast }$，若存在 Q-线性收敛于 0 的非负序列 { t k } \{t_k\} {tk​} 并且
$$\Vert x^k-x^{\ast }\Vert ⩽t_k$$

对任意的 $k$ 成立，则称算法 (点列) 是 R-线性收敛的. 类似地，可定义 R-超线性收敛和 R-二次收敛等收敛速度. 从 R-收敛速度的定义可以看出序列 { ∥ x k − x ∗ ∥ } \{\|x^k-x^*\|\} {∥xk−x∗∥} 被另一趋于 0 的序列 { t k } \{t_k\} {tk​} 控制. 当知道 $t_k$ 的形式时，我们也称算法 (点列) 的收敛速度为 $\mathcal{O}(t_k)$.

定理 6.2 指出使用精确线搜索的梯度法在正定二次问题上有 Q-线性收敛速度。线性收敛速度的常数和矩阵 $A$ 最大特征值与最小特征值之比有关。从等高线角度来看，这个比例越大则 $f(x)$ 的等高线越扁平，迭代路径折返频率会随之变高，梯度法收敛也就越慢。这个结果其实说明了梯度法的一个很重大的缺陷：当目标函数的海瑟矩阵条件数较大时，它的收敛速度会非常缓慢。

接下来介绍当 $f(x)$ 为梯度利普希茨连续的凸函数时，梯度法 (6.2.1) 的收敛性质。
首先，回顾一下定义 2.4 梯度利普希茨连续：给定可微函数 $f$，若存在 $L>0$，对任意的 $x, y\in $\ast \ast dom\ast \ast$f$ 有
$$\Vert \nabla f(x)-\nabla f(y)\Vert \le L\Vert x-y\Vert ,$$

则称 $f$ 是梯度利普希茨连续的，相应利普希茨常数为 $L$。有时也简记为梯度 $L$-利普希茨连续或 $L$-光滑。
引理 2.1 二次上界引理：设可微函数 $f(x)$ 的定义域 dom $f={\mathbb{R}}^n$，且为梯度 $L$-利普希茨连续的，则函数 $f(x)$ 有二次上界：
$$f(y)\le f(x)+\nabla f(x{)}^{\mathrm{T}}(y-x)+\frac{L}{2}\Vert y-x{\Vert }^2,\forall x,y\in \mathrm{dom}f$$

定理 6.3 (梯度法在凸函数上的收敛性) 设函数 $f(x)$ 为凸的梯度 $L$-利普希茨连续函数，极小值 $f^{\ast }=f(x^{\ast })=\underset{x}{\inf }f(x)$ 存在且可达。如果步长 ${\alpha }_k$ 取为常数 $\alpha$ 且满足 $0<\alpha <\frac{1}{L}$，那么由迭代 $x^{k+1}=x^k-{\alpha }_k\nabla f(x^k)$ 得到的点列 { x k } \{x^k\} {xk} 的函数值收敛到最优值，且在函数值的意义下收敛速度为 $\mathcal{O}\left(\frac{1}{k}\right)$.

证明. 因为函数 $f$ 是利普希茨可微函数，对任意的 $x$, 根据二次上界引理得到，
$$\begin{array}{r}f(x-\alpha \nabla f(x))⩽f(x)-\alpha \left(1-\frac{L\alpha }{2}\right)\Vert \nabla f(x){\Vert }^2\end{array}(\mathrm{6.2.3})$$

记 $\tilde{x}=x-\alpha \nabla f(x)$ 并限制 $0<\alpha <\frac{1}{L}$, 我们有
$$\begin{array}{rl}f(\tilde{x})& ⩽f(x)-\frac{\alpha }{2}\Vert \nabla f(x){\Vert }^2\\ & ⩽f^{\ast }+\nabla f(x{)}^{\mathrm{T}}(x-x^{\ast })-\frac{\alpha }{2}\Vert \nabla f(x){\Vert }^2\\ & =f^{\ast }+\frac{1}{2\alpha }\left(\Vert x-x^{\ast }{\Vert }^2-\Vert x-x^{\ast }-\alpha \nabla f(x){\Vert }^2\right)\\ & =f^{\ast }+\frac{1}{2\alpha }(\Vert x-x^{\ast }{\Vert }^2-\Vert \tilde{x}-x^{\ast }{\Vert }^2)\end{array}$$

其中第一个不等式是由于 $0<\alpha <\frac{1}{L}$，第二个不等式为 $f$ 的凸性. 在上式中取 $x=x^{i-1},\tilde{x}=x^i$ 并将不等式对 $i=1,2,\cdot \cdot \cdot ,k$ 求和得到
$$\begin{array}{rl}\sum _{i=1}^k(f(x^i)-f^{\ast })& ⩽\frac{1}{2\alpha }\sum _{i=1}^k(\Vert x^{i-1}-x^{\ast }{\Vert }^2-\Vert x^i-x^{\ast }{\Vert }^2)\\ & =\frac{1}{2\alpha }(\Vert x^0-x^{\ast }{\Vert }^2-\Vert x^k-x^{\ast }{\Vert }^2)\\ & ⩽\frac{1}{2\alpha }\Vert x^0-x^{\ast }{\Vert }^2\end{array}$$

由于 $f(x^i)$ 是非增的，所以
$$f(x^k)-f^{\ast }⩽\frac{1}{k}\sum _{i=1}^k(f(x^i)-f^{\ast })⩽\frac{1}{2k\alpha }\Vert x^0-x^{\ast }{\Vert }^2$$

如果函数 $f$ 还是 $m$-强凸函数，则梯度法的收敛速度会进一步提升为 $Q$-线性收敛。

在给出收敛性证明之前，我们需要以下的引理来揭示凸的梯度 $L$-利普希茨连续函数的另一个重要性质。

引理 6.1 设函数 $f(x)$ 是 ${\mathbb{R}}^n$ 上的凸可微函数，则以下结论等价：
(1) $f$ 的梯度为 $L$-利普希茨连续的；
(2) 函数 $g(x)\stackrel{\mathrm{def}}{=}\frac{L}{2}{x}^{\mathrm{T}}x-f(x)$ 是凸函数；
(3) $\nabla f(x)$ 有余强制性，即对任意的 $x,y\in {\mathbb{R}}^n$，有
$$(\nabla f(x)-\nabla f(y){)}^{\mathrm{T}}(x-y)⩾\frac{1}{L}\Vert \nabla f(x)-\nabla f(y){\Vert }^2(\mathrm{6.2.4})$$

证明.
$(1)⟹(2)$
我们已知 $f(x)$ 是凸可微函数且其梯度为 $L$ -利普希茨连续的，则我们需要证明函数 $g(x)=\frac{L}{2}{x}^{\mathrm{T}}x-f(x)$ 是凸函数。为了证明 $g(x)$ 是凸函数，我们需要证明对于任意的 $x,y\in {\mathbb{R}}^n$ 和 $0⩽\lambda ⩽1$，有
$$g(\lambda x+(1-\lambda )y)⩽\lambda g(x)+(1-\lambda )g(y)$$

即需要证明 $g(x)$ 的上凸性。首先，由于 $f(x)$ 是凸函数，则根据凸函数的定义，对于任意的 $x,y\in {\mathbb{R}}^n$ 和 $0\le \lambda \le 1$，有
$$f(\lambda x+(1-\lambda )y)⩽\lambda f(x)+(1-\lambda )f(y)$$

因为 $g(x)=\frac{L}{2}{x}^{\mathrm{T}}x-f(x)$，所以我们可以把上式左右两边都加上 $\frac{L}{2}(\lambda x+(1-\lambda )y{)}^{\mathrm{T}}(\lambda x+(1-\lambda )y)$，得到
$$g(\lambda x+(1-\lambda )y)+\frac{L}{2}(\lambda x+(1-\lambda )y{)}^{\mathrm{T}}(\lambda x+(1-\lambda )y)⩽\lambda g(x)+\frac{L}{2}{x}^{\mathrm{T}}x-f(x)+(1-\lambda )g(y)+\frac{L}{2}{y}^{\mathrm{T}}y-f(y)$$

简化后可得
$$g(\lambda x+(1-\lambda )y)⩽\lambda g(x)+(1-\lambda )g(y)+\frac{L}{2}\lambda (1-\lambda )(x-y{)}^{\mathrm{T}}(x-y)$$

因为$L$ 是 $f(x)$ 的梯度的 Lipschitz 常数，因此有
$$\Vert \nabla f(x)-\nabla f(y)\Vert \le L\Vert x-y\Vert$$

根据梯度的定义，我们有
$$\nabla f(x{)}^{\mathrm{T}}(x-y)⩾f(x)-f(y)+\frac{L}{2}\Vert x-y{\Vert }^2$$

同样地，我们可以得到
$$\nabla f(y{)}^{\mathrm{T}}(x-y)⩾f(x)-f(y)+\frac{L}{2}\Vert x-y{\Vert }^2$$

将两式相减，可得
$$(\nabla f(x)-\nabla f(y){)}^{\mathrm{T}}(x-y)⩾L\Vert x-y{\Vert }^2$$

根据此式，我们可以继续推导得到
$$g(\lambda x+(1-\lambda )y)⩽\lambda g(x)+(1-\lambda )g(y)+\frac{L}{2}\lambda (1-\lambda )\Vert x-y{\Vert }^2=\lambda g(x)+(1-\lambda )g(y)+\frac{L}{2}\Vert \lambda x+(1-\lambda )y-x{\Vert }^2$$

由此可知 $g(x)$ 是凸的。

$(2)⟹(3)$ 构造辅助函数
$$\begin{array}{r}{f}_x(z)=f(z)-\nabla f(x{)}^{\mathrm{T}}z\\ f_y(z)=f(z)-\nabla f(y{)}^{\mathrm{T}}z\end{array}$$

首先验证 $f_x(z)$ 为凸函数。考虑 $f_x(z)$，其定义为 $f_x(z)=f(z)-\nabla f(x{)}^{\mathrm{T}}z$。要证明 $f_x(z)$ 是凸函数，需要验证对于任意的 $z_1,z_2\in {\mathbb{R}}^n$ 和 $0\le \lambda \le 1$，有
$$f_x(\lambda z_1+(1-\lambda )z_2)\le \lambda f_x(z_1)+(1-\lambda )f_x(z_2)$$

考虑左边的表达式：
$$\begin{array}{rl}{f}_x(\lambda z_1+(1-\lambda )z_2)& =f(\lambda z_1+(1-\lambda )z_2)-\nabla f(x{)}^{\mathrm{T}}(\lambda z_1+(1-\lambda )z_2)\\ & =\lambda f(z_1)+(1-\lambda )f(z_2)-\lambda \nabla f(x{)}^{\mathrm{T}}{z}_1-(1-\lambda )\nabla f(x{)}^{\mathrm{T}}{z}_2\end{array}$$

再考虑右边的表达式：
$$\begin{array}{rl}\lambda f_x(z_1)+(1-\lambda )f_x(z_2)& =\lambda (f(z_1)-\nabla f(x{)}^{\mathrm{T}}{z}_1)+(1-\lambda )(f(z_2)-\nabla f(x{)}^{\mathrm{T}}{z}_2)\\ & =\lambda f(z_1)+(1-\lambda )f(z_2)-\lambda \nabla f(x{)}^{\mathrm{T}}{z}_1-(1-\lambda )\nabla f(x{)}^{\mathrm{T}}{z}_2\end{array}$$

由上述计算可知，$f_x(z)$ 满足凸函数的定义，因此 $f_x(z)$ 是凸函数。同理可证明 $f_y(z)$ 也是凸函数。
根据已知条件，$g_x(z)=\frac{L}{2}{z}^{\mathrm{T}}z-f_x(z)$ 关于 $z$ 是凸函数. 根据凸函数的性质，我们有
$$g_x(z_2)⩾g_x(z_1)+\nabla g_x(z_1{)}^{\mathrm{T}}(z_2-z_1),\forall z_1,z_2\in {\mathbb{R}}^n.$$

将 $g_x(z)$ 展开得：
$$\begin{array}{c}{g}_x(z_2)=\frac{L}{2}{z}_2^{\mathrm{T}}{z}_2-f_x(z_2)\\ g_x(z_1)=\frac{L}{2}{z}_1^{\mathrm{T}}{z}_1-f_x(z_1)\end{array}$$

将上述两个式子代入凸函数性质的公式中，得到
$$\frac{L}{2}{z}_2^{\mathrm{T}}{z}_2-f_x(z_2)\ge \frac{L}{2}{z}_1^{\mathrm{T}}{z}_1-f_x(z_1)+\nabla g_x(z_1{)}^{\mathrm{T}}(z_2-z_1)$$

移项整理得到
$$f_x(z_1)-f_x(z_2)\le \frac{L}{2}(z_2^{\mathrm{T}}{z}_2-z_1^{\mathrm{T}}{z}_1)-\nabla g_x(z_1{)}^{\mathrm{T}}(z_2-z_1)$$

因为 $f_x(z_1)-f_x(z_2)$ 在右端是一个二次函数，所以 $f_x(z)$ 有二次上界，且对应的系数为 $L$ 。
注意到 $\nabla f_x(x)=0$, 这说明 $x$ 是 $f_x(z)$ 的最小值点. 再由梯度 $L$-利普希茨函数的性质，
$$\begin{array}{rl}{f}_x(y)-f_x(x)& =f(y)-f(x)-\nabla f(x{)}^{\mathrm{T}}(y-x)\\ & ⩾\frac{1}{2L}\Vert \nabla f_x(y){\Vert }^2=\frac{1}{2L}\Vert \nabla f(y)-\nabla f(x){\Vert }^2.\end{array}$$

同理，对 $f_y(z)$ 进行类似的分析可得
$$f(x)-f(y)-\nabla f(y{)}^{\mathrm{T}}(x-y)⩾\frac{1}{2L}\Vert \nabla f(y)-\nabla f(x){\Vert }^2.$$

将以上两式不等号左右分别相加，可得余强制性 (6.2.4).

$(3)⟹(1)$ 由余强制性和柯西不等式，
$$\begin{array}{rl}\frac{1}{L}\Vert \nabla f(x)-\nabla f(y){\Vert }^2& ⩽(\nabla f(x)-\nabla f(y){)}^{\mathrm{T}}(x-y)\\ & ⩽\Vert \nabla f(x)-\nabla f(y)\Vert \Vert x-y\Vert \end{array}$$

整理后即可得到 $f(x)$ 是梯度 $L$-利普希茨连续的.

引理 6.1 说明在 $f$ 为凸函数的条件下，梯度 L-利普希茨连续、二次上界、余强制性三者是等价的，知道其中一个性质就可推出剩下两个。接下来给出梯度法在强凸函数下的收敛性。

定理 6.4 (梯度法在强凸函数上的收敛性) 设函数 $f(x)$ 为 $m$-强凸的梯度 $L$-利普希茨连续函数，$f^{\ast }=f(x^{\ast })=\underset{x}{\inf }f(x)$ 存在且可达。如果步长 $\alpha$ 满足 $0<\alpha ⩽\frac{2}{m+L}$，那么由梯度下降法 (6.2.1) 迭代得到的点列 { x k } \{x^k\} {xk} 收敛到 $x^{\ast }$，且为 $Q$-线性收敛。

证明. 首先根据 $f$ 强凸且 $\nabla f$ 利普希茨连续，可得
$$g(x)=f(x)-\frac{m}{2}{x}^{\mathrm{T}}x$$

为凸函数且 $\frac{L-m}{2}{x}^{\mathrm{T}}x-g(x)$为凸函数. 由引理 6.1 可得 $g(x)$ 是梯度 ($L-m$)-利普希茨连续的. 再次利用引理 6.1 可得关于 $g(x)$ 的余强制性
$$(\nabla g(x)-\nabla g(y){)}^{\mathrm{T}}(x-y)⩾\frac{1}{L-m}\Vert \nabla g(x)-\nabla g(y){\Vert }^2(\mathrm{6.2.5})$$

代入 $g(x)$ 的表达式，可得
$$\begin{array}{r}(\nabla f(x)-\nabla f(y){)}^{\text{T}}(x-y)⩾\frac{mL}{m+L}\Vert x-y{\Vert }^2+\frac{1}{m+L}\Vert \nabla f(x)-\nabla f(y){\Vert }^2.\end{array}(\mathrm{6.2.6})$$

再估计固定步长下梯度法的收敛速度. 设步长 $\alpha \in \left(0,\frac{2}{m+L}\right]$, 对 $x^k,x^{\ast }$ 应用上式并注意到 $\nabla f(x^{\ast })=0$ 得
$$\begin{array}{rl}\Vert x^{k+1}-x^{\ast }{\Vert }^2& =\Vert x^k-\alpha \nabla f(x^k)-x^{\ast }{\Vert }^2\\ & =\Vert x^k-x^{\ast }{\Vert }^2-2\alpha \nabla f(x^k{)}^{\mathrm{T}}(x^k-x^{\ast })+{\alpha }^2\Vert \nabla f(x^k){\Vert }^2\\ & ⩽\left(1-\alpha \frac{2mL}{m+L}\right)\Vert x^k-x^{\ast }{\Vert }^2+\alpha \left(\alpha -\frac{2}{m+L}\right)\Vert \nabla f(x^k){\Vert }^2\\ & ⩽\left(1-\alpha \frac{2mL}{m+L}\right)\Vert x^k-x^{\ast }{\Vert }^2\end{array}$$

$$⟹\Vert x^k-x^{\ast }{\Vert }^2⩽c^k\Vert x^0-x^{\ast }{\Vert }^2,c=1-\alpha \frac{2mL}{m+L}<1,$$

即在强凸函数的条件下，梯度法是 $Q$-线性收敛的.

6.2.2 Barzilai-Borwein 方法

由上一小节可以知道，当问题的条件数很大，也即问题比较病态时，梯度下降法的收敛性质会受到很大影响。Barzilai-Borwein (BB) 方法是一种特殊的梯度法，经常比一般的梯度法有着更好的效果。从形式上来看，BB 方法的下降方向仍是点 $x^k$ 处的负梯度方向 $-\nabla f(x^k)$，但步长 ${\alpha }_k$ 并不是直接由线搜索算法给出的。考虑梯度下降法的格式：
$$x^{k+1}=x^k-{\alpha }_k\nabla f(x^k)⟺x^{k+1}=x^k-D^k\nabla f(x^k)$$

其中 $D^k={\alpha }_{k}I$。BB 方法选取的 ${\alpha }_k$ 是如下两个最优问题之一的解：
$$\underset{\alpha }{\min }\Vert \alpha y^{k-1}-s^{k-1}{\Vert }^2(\mathrm{6.2.7})$$

$$\underset{\alpha }{\min }\Vert y^{k-1}-{\alpha }^{-1}{s}^{k-1}{\Vert }^2(\mathrm{6.2.8})$$

其中引入记号 $s^{k-1}\stackrel{\mathrm{def}}{=}{x}^k-x^{k-1}$ 以及 $y^{k-1}\stackrel{\mathrm{def}}{=}\nabla f(x^k)-\nabla f(x^{k-1})$。

对问题 (6.2.7) 和 (6.2.8) 分别求导取零，得到的解分别为
$${\alpha }_{BB1}^k\stackrel{\mathrm{def}}{=}\frac{(s^{k-1}{)}^{\mathrm{T}}{y}^{k-1}}{(y^{k-1}{)}^{\mathrm{T}}{y}^{k-1}}\text{和}{\alpha }_{BB2}^k\stackrel{\mathrm{def}}{=}\frac{(s^{k-1}{)}^{\mathrm{T}}{s}^{k-1}}{(s^{k-1}{)}^{\mathrm{T}}{y}^{k-1}}(\mathrm{6.2.9})$$

因此可以得到 BB 方法的两种迭代格式：
$$\begin{array}{rl}{x}^{k+1}& =x^k-{\alpha }_{\text{BB}1}^k\nabla f(x^k)(\mathrm{6.2.10}a)\\ x^{k+1}& =x^k-{\alpha }_{\text{BB}2}^k\nabla f(x^k)(\mathrm{6.2.10}b)\end{array}$$

计算两种 BB 步长的任何一种仅仅需要函数相邻两步的梯度信息和迭代点信息，不需要任何线搜索算法即可选取算法步长。BB 方法计算出的步长可能过大或过小，因此我们还需要将步长做上界和下界的截断，即选取 $0<{\alpha }_m<{\alpha }_M$ 使得

$${\alpha }_m⩽{\alpha }_k⩽{\alpha }_M$$

还需注意的是，BB 方法本身是非单调方法，有时也配合非单调收敛准则使用以获得更好的实际效果。算法 6.2 给出了一种 BB 方法的框架。

# 算法 6.2 非单调线搜索的 BB 方法
import numpy as np
# 定义Barzilai-Borwein方法函数
def BB_method(x0, alpha0, M, c1, beta, epsilon, alpha_m, alpha_M):
    x = x0
    alpha = alpha0
    k = 0 #迭代次数
    x_history = [x]
    # 开始迭代，直到梯度满足精度要求
    while np.linalg.norm(grad(x)) > epsilon:
        while f(x - alpha * grad(x)) >= max([f(x - j) for j in range(min(k, M) + 1)]) - c1 * alpha * np.linalg.norm(grad(x))**2:
            alpha = beta * alpha
        x_next = x - alpha * grad(x)
        
        if k > 0:
            s = x - x_prev
            y = grad(x) - grad(x_prev)
            alpha = np.dot(s, y) / np.dot(y, y)
            # alpha_BB2 = np.dot(s, s) / np.dot(s, y)
            alpha = np.clip(alpha, alpha_m, alpha_M)  # 使用clip函数限制alpha的取值范围
        
        x_prev = x
        x = x_next
        x_history.append(x)
        k = k + 1
    return x_history, k

我们仍然使用例 6.2 来说明 BB 方法的迭代过程．

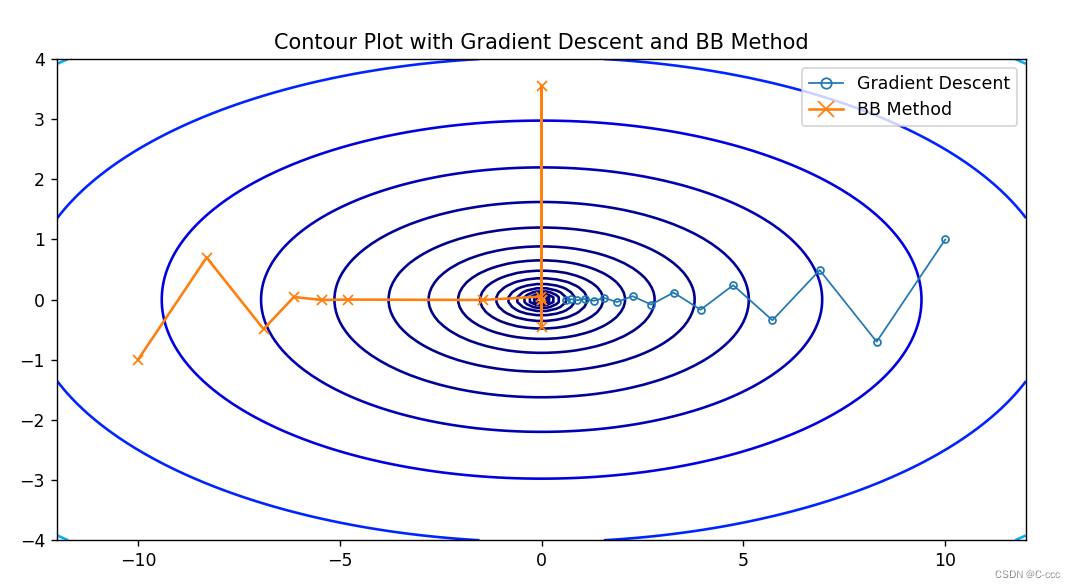
例 6.3 (二次函数的 BB 方法) 设二次函数 $f(x,y)=x^2+10y^2$，并使用 BB 方法进行迭代，初始点为 (-10,-1)，结果如图 6.5 所示。为了方便对比，我们也在此图中描绘了梯度法的迭代过程，可以很明显看出 BB 方法的收敛速度较快，在经历 11 次迭代后已经接近最优值点。BB 方法是非单调方法。实际上，对于正定二次函数，BB 方法有 R-线性收敛速度。

# 定义目标函数和其梯度函数
import numpy as np
import matplotlib.pyplot as plt
def f(x):
    return x[0]**2 + 10 * x[1]**2
def grad(x):
    return np.array([2*x[0], 20*x[1]])

# 梯度下降法
def gradient_descent(x0, alpha, epsilon, max_iter):
    x = x0
    k = 0
    x_history = [x]
    while np.linalg.norm(grad(x)) > epsilon and k < max_iter:
        x = x - alpha * grad(x)
        x_history.append(x)
        k += 1
    return x_history, k

x0 = np.array([10, 1])
x1 = np.array([-10, -1])
alpha0 = 0.085
M = 5
c1 = 0.1
beta = 0.5
epsilon = 1e-6
alpha_m = 1e-6
alpha_M = 1e6
# 运行梯度下降法
max_iter = 15
gd_history, gd_k = gradient_descent(x0, alpha0, epsilon, max_iter)
# 运行Barzilai-Borwein方法
bb_history, bb_k = BB_method(x1, alpha0, M, c1, beta, epsilon, alpha_m, alpha_M)
print("gd迭代次数:",gd_k,", bb迭代次数:",bb_k)
'''gd迭代次数: 15 , bb迭代次数: 11'''
# 定义网格点
x = np.linspace(-12, 12, 100)
y = np.linspace(-4, 4, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2  # 定义目标函数

# 绘制目标函数的等高线图及优化路径
plt.figure(figsize=(10, 5))
plt.contour(X, Y, Z, levels=np.logspace(-2, 3, 20), cmap='jet')  # levels 参数控制等高线的密集程度
plt.plot([x[0] for x in gd_history], [x[1] for x in gd_history], marker='o',markersize=4, linewidth=1, markerfacecolor='none', label='Gradient Descent')
plt.plot([x[0] for x in bb_history], [x[1] for x in bb_history], marker='x', label='BB Method')  # 添加优化路径
plt.legend(loc='best', markerscale=1.5)  # 设置标签位置为最佳位置，调整图例的大小
plt.title('Contour Plot with Gradient Descent and BB Method')
plt.show()

参考教材：《最优化：建模、算法与理论》