【鲁棒状态估计】提出了一种类似卡尔曼滤波器的滤波器，并与经典最坏情况下的鲁棒设计滤波器进行了比较（Matlab代码实现）

 💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码及详细文章

---

💥1 概述

摘要：
本文讨论了当只有一个粗略模型可用时，系统的估计和过滤问题。基于经典正则化最小二乘问题的修改版本，提出了一个新的估计设计标准，考虑测量和创新作为可能的不确定性源。在高斯假设下，它表现为最大后验贝叶斯估计的上界。通过利用非光滑分析工具获得最佳解，最优解揭示了残差空间中估计的非变化的最佳区域。这种方法以递归形式从随机角度提供了稳健的估计器。为了说明问题，提出了一种类似卡尔曼滤波器的滤波器，并与经典最坏情况下的稳健设计滤波器进行了比较。从使用了广泛的科学和工程中，从含噪声观测值中估计一组未知参数的问题有着广泛应用。然而很常见的是，生成数据的精确模型可能未知，并且需要一个具有鲁棒性的估计器。

在文献中，鲁棒状态估计主要有两种方法。 第一种方法是H∞估计，试图将输入噪声对估计误差的最坏能量增益最小化。第二种方法是所谓的保证成本估计，其中设计了一个满足误差上界的估计算法。此外，还探索了一种基于确定性正则化最小二乘问题的不同方法，用于设计稳健的估计器。然而，如果模型和测量的不确定性很大，这些方法都涉及基于最坏情况的优化，并且在解决方案中可能会携带很高的保守性。为了获得一个针对了解不足的模型量身定制的鲁棒估计器，这封信采用了一种更少保守的问题的随机观点，并依赖经典正则化最小二乘问题的修改版本。这使我们能够获取最小二乘稳健估计量和卡尔曼滤波器的更新阶段。

该立场的主要贡献是为了在新的随机建模工具中考虑模型不确定性而提出的静态估计器和滤波模型。结果表明，在高斯假设下，估计标准表现为最大后验贝叶斯估计的上界。

所得滤波器的一个显著特征是，在某些情况下，最佳估计仍然是先验，而不是后验，在考虑系统动态所提供的先验信任和新测量的不完整模型场景之间进行权衡。

这种行为是通过估计变化的绝对值调制的随机噪声嵌入模型中，据我们所知，在稳健滤波的现有文献中并没有看到这种情况。与那些不同，所得滤波器增益是非线性的。

📚2 运行结果

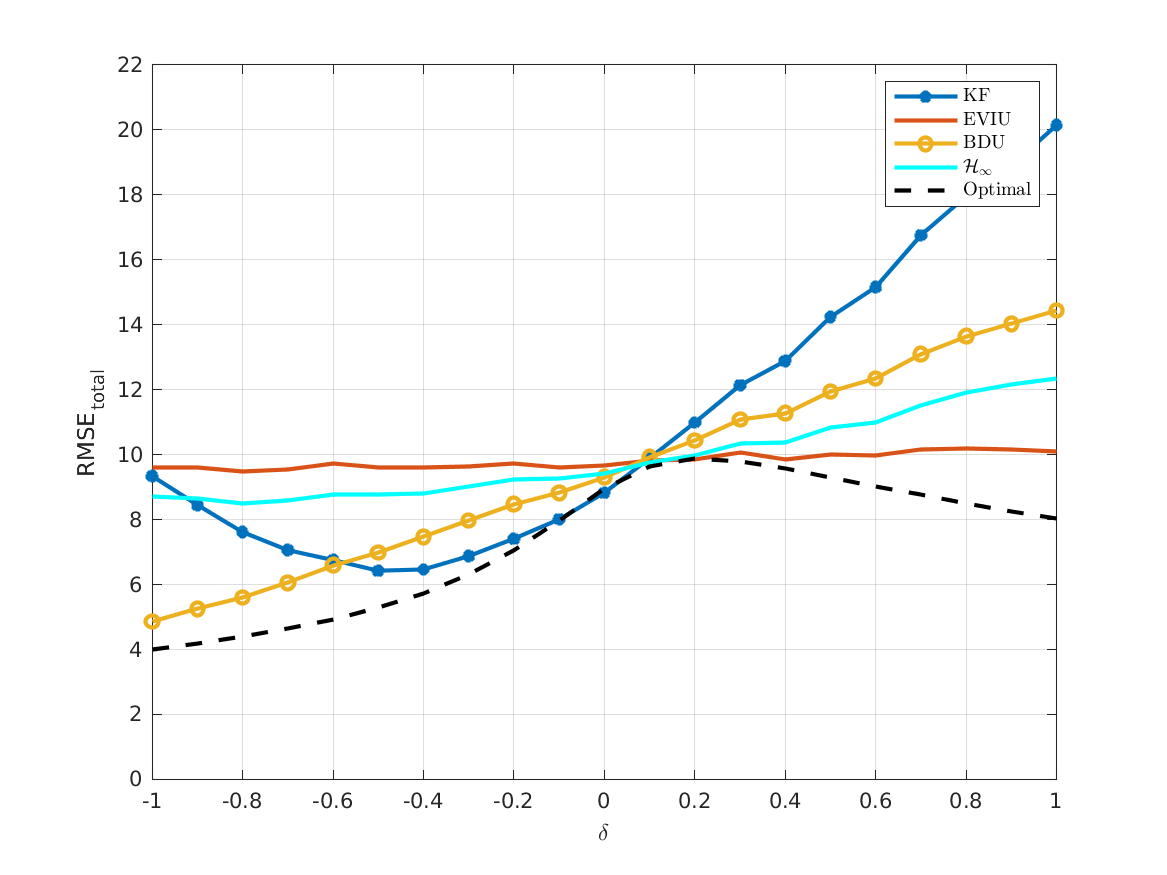
%% Plot results
figure(1)
p1=plot(a,sqrt(mmse),'*-','linewidth',2);
hold on
p2=plot(a,sqrt(mmse2),'-','linewidth',2);
p3=plot(a,sqrt(mmse_s),'o-','linewidth',2);
p5=plot(a,sqrt(mmse_hinf),'c-','linewidth',2);
p4=plot(a,sqrt(mmse_opt),'--k','linewidth',2);
legend([p1,p2,p3,p5,p4],'KF','EVIU','BDU','$\mathcal{H}_\infty$','Optimal','Interpreter','latex')
ylabel('RMSE_{total}')
xlabel('\delta')
axis([-1 1 0 22])
grid on

复现结果：

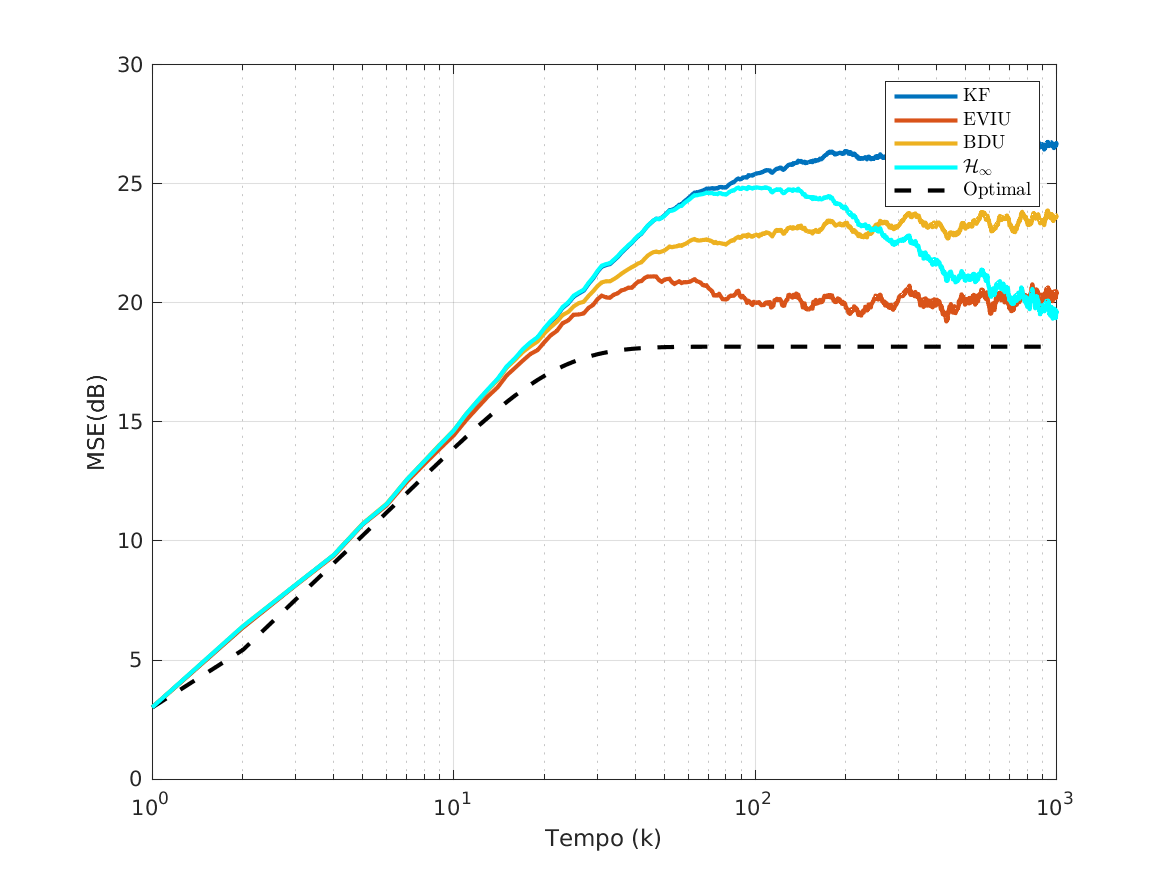
figure(2)
%Worst-case (delta=1)
p1=semilogx(10*log10(mse),'-','linewidth',2);
hold on
p2=semilogx(10*log10(mse2),'linewidth',2);
p3=semilogx(10*log10(mse_s),'-','linewidth',2);
p4=semilogx(10*log10(trP_opt),'--k','linewidth',2);
p5=semilogx(10*log10(mse_hinf),'c-','linewidth',2);
ylabel('MSE(dB)')
xlabel('Tempo (k)')
grid on
legend([p1,p2,p3,p5,p4],'KF','EVIU','BDU','$\mathcal{H}_\infty$','Optimal','Interpreter','latex')

部分代码：

%% Simulation
N=1000; %time horizon
a=-1:0.1:1; % grid for uncertain parameter
H=H0; %output matrix is considered exactly
gamma=99; %gain for the Hinf Filter

%Make a grid on [-1,1] for the uncertain parameter and apply simultaneosly
%the EVIU, BDU, Hinf and Kalman filter.
for i=1:length(a)
    A=A0+a(i)*A1; %define 'true' dynamic matrix
    % Monte Carlo Simulation
    for j=1:500
        %% Initialization
        clear x hx m hx2 hx_opt hx_s hx_hinf P P2 P_s P_hinf P_opt
        x(:,1)=1*ones(n,1);%real states
        hx(:,1)=zeros(n,1);%classic kalman states
        hx_opt(:,1)=zeros(n,1);%opt states
        m=zeros(n,1);
        S=zeros(n,1); %beta0
        hx2=hx; %eviu states
        hx_s=hx; %BDU states
        hx_hinf=hx; %hinf states
        P=eye(n); %initial covariance
        L=P;
        P_s=P; %covariance for BDU filter
        P2=P; %covariance for EVIU filter
        Phinf=P; %covariance for Hinf filter
        P_opt=P; %covariance for optimal filter
        trP(1)=trace(P); %trace of KF covariance
        trP2(j,1)=trP(1); %trace of EVIU covariance
        trP_opt(j,1)=trP(1); %trace of Optimal covariance
        trP_s(j,1)=trP(1); %trace of BDU covariance
        trP_hinf(j,1)=trP(1); %trace of Hinf covariance
        mse(j,1)=norm(hx(:,1)-x(:,1))^2; %KF error
        mse2(j,1)=mse(j,1); % EVIU error
        mse_opt(j,1)=mse(j,1); % Minimum error
        mse_hinf(j,1)=mse(j,1); % Hinf error
        mse_s(j,1)=mse(j,1); % BDU error
        %time simulation
        for k=1:N-1
            %% real system
            x(:,k+1)=A*x(:,k)+sigma*randn(n,1);
            y(:,k+1)=H*x(:,k+1)+nu*randn(p,1);
            %% Classic Kalman Filter (hx)
            [hx(:,k+1),P]=kalman_filter(A0,H0,Q,R,hx(:,k),P,y(:,k+1));
            trP(k+1)=trace(P);
            mse(j,k+1)=norm(x(:,k+1)-hx(:,k+1))^2;
            %% EVIU Filter (hx2)
        [hx2(:,k+1),P2,m,L,S(:,k+1)]=eviu_filter(A0,H0,sigmas,Q,R,hx2(:,k),P2,m,L,S(:,k),y(:,k+1));
            trP2(j,k+1)=trace(P2);
            mse2(j,k+1)=norm(x(:,k+1)-hx2(:,k+1))^2;
            %% Optimal Filter (Kalman with exactly model)
            [hx_opt(:,k+1),P_opt]=kalman_filter(A,H,Q,R,hx_opt(:,k),P_opt,y(:,k+1));
            trP_opt(j,k+1)=trace(P_opt);
            %% BDU Filter
            [hx_s(:,k+1),P_s]=BDU_filter(A0,H0,M,Ef,Eg,G,Q,R,hx_s(:,k),P_s,y(:,k+1));
            trP_s(j,k+1)=trace(P_s);
            mse_s(j,k+1)=norm(x(:,k+1)-hx_s(:,k+1))^2;
            %% Hinf filter
            [hx_hinf(:,k+1),Phinf]=hinf_filter(A0,H0,G,Q,R,hx_hinf(:,k),Phinf,y(:,k+1),eye(n),gamma);
            trP_hinf(j,k+1)=trace(Phinf);
            mse_hinf(j,k+1)=norm(x(:,k+1)-hx_hinf(:,k+1))^2;
        end
    end
 mse=mean(mse); %KF
    mse2=mean(mse2); %EVIU
    mse_s=mean(mse_s); %BDU
    trP_opt=mean(trP_opt); %Optimal
    mse_hinf=mean(mse_hinf); %Hinf
    mmse(i)=mean(mse); %KF
    mmse2(i)=mean(mse2); %EVIU
    mmse_s(i)=mean(mse_s); %BDU
    mmse_hinf(i)=mean(mse_hinf); %Hinf
    mmse_opt(i)=mean(trP_opt); % Optimal

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

🌈4 Matlab代码及详细文章