【用于电能质量分类的ML和DWT】智能电网中高级电能质量干扰鲁棒分类器的机器学习应用（Matlab代码实现)

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

在智能电网中，确保电能质量的稳定和可靠对于提供可持续的电力供应至关重要。为了实现高级电能质量干扰的鲁棒分类，可以使用机器学习和小波变换（DWT）等技术。

机器学习在电力系统中的应用是基于对大量数据的学习和模式识别。对于电能质量分类，可以使用监督学习算法，如支持向量机（SVM）、随机森林（Random Forest）或神经网络等，来训练一个分类器模型。

1. 数据采集：收集包含各种电能质量干扰的实时数据，如电压波形、电流波形、频谱分析等。

2. 特征提取：从原始数据中提取有意义的特征，这些特征可以包括频率、振幅、谐波含量等。特征提取的目的是将复杂的波形数据转化为计算机可以理解的数字特征。

3. 数据标记：对采集的数据进行标记，将不同类型的电能质量干扰分类。例如，对电压暂降、电压暂升、电流谐波等进行分类标记。

4. 数据划分：将标记好的数据分为训练集和测试集。训练集用于训练分类器模型，测试集用于评估模型的性能。

5. 模型训练：使用机器学习算法，根据训练集的特征和标签，训练一个分类器模型。这个模型将学习不同类型电能质量干扰的模式和规律。

6. 模型评估：使用测试集评估模型的分类性能，如准确率、召回率、F1分数等。

一旦分类器模型训练完毕，它就可以用于实时数据的分类。将实时采集的电能质量数据输入到模型中，模型会根据学习到的模式和规律将其分类为不同的干扰类型。

小波变换（DWT）可以用于对电能质量数据进行频域分析和时域分析。DWT可以提供不同尺度下的频谱信息和时序信息，有助于提取更多的特征。将DWT与机器学习相结合，可以提高分类的准确性和鲁棒性。

综上所述，机器学习和小波变换是在智能电网中实现高级电能质量干扰鲁棒分类的关键技术。通过训练一个针对电能质量的分类器模型，并利用DWT对数据进行分析，可以实现对电能质量干扰的准确分类与识别。这些技术的应用可以提高电力系统的可靠性和稳定性，进一步推动智能电网的发展。

新设备的插入、数据流的增加、间歇性的生成和大规模的计算机化大大增加了当前电气系统的复杂性。这种增长导致了必要的变化，例如需要更智能的电网来适应这种不同的现实。以大数据、机器学习（ML）、深度学习（DL）和模式识别为代表的人工智能（AI）技术的产生代表了基于信息和知识的社会和全球发展的新时代。随着最近的智能电网（SG），使用使用这种智能的技术将更加必要。本论文研究了使用高级信号处理和 ML 算法来创建 SG 中高级电能质量干扰的鲁棒分类器。为此，使用随机元素生成了已知的PQ干扰模型，以接近实际应用。从这些模型中，这些干扰的性能产生了数千个信号。使用离散小波变换（DWT）的信号处理技术来提取信号的主要特征。本研究旨在使用 ML 算法根据各自的特征对这些数据进行分类。ML 算法经过训练、验证和测试。此外，还分析了准确性和混淆矩阵，将结果背后的逻辑联系起来。数据生成、特征提取和特征选择阶段在 MATLAB 软件中执行。分类学习器工具箱用于训练、验证和测试 27 种不同的 ML 算法，并评估每种性能。工作的所有阶段以前都是理想化的，因此可以正确开发和执行。结果表明，三次支持向量机（SVM）分类器在所有算法中均实现了最高精度，表明了所提分类方法的有效性。对结果的考虑被解释为解释每种技术的性能，其关系及其各自的理由。

📚2 运行结果

 

 

 

 

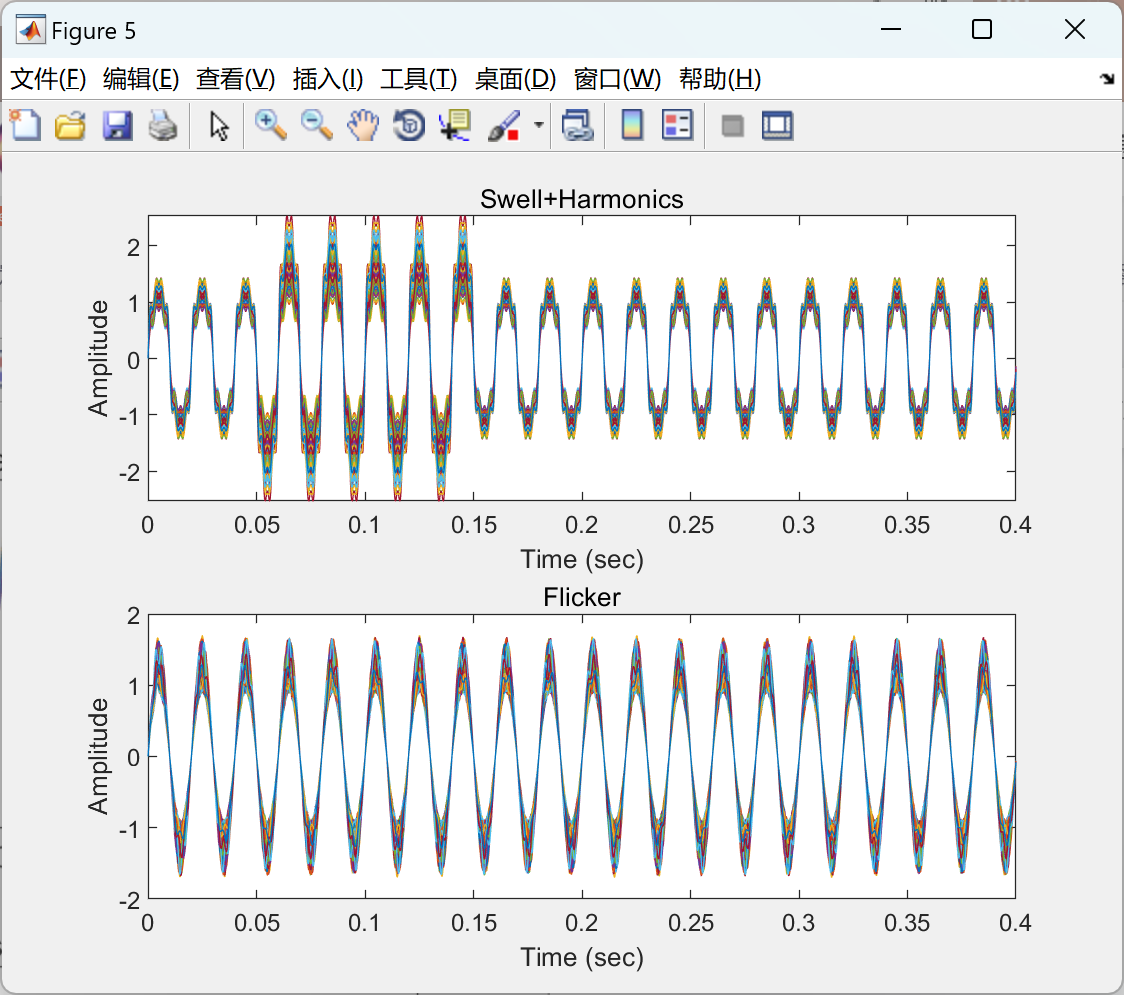
部分代码：

[c1,c2] = dwt(Swell_harmonic,'dmey');% coeficientes discretos
en1 = wentropy(Swell_harmonic,'shannon');% entropia do sinal original
en2 = wentropy(c1,'shannon');% entropia dos coeficiente aproximados (approximation coefficients)
en3 = wentropy(c2,'shannon');% entropia dos coeficientes detalhados (detail coefficients)
% coeff = cwt(vwave); %coeficientes
energy = sqrt(sum(abs(c2).^2,2)); %energia dos coeficientes continuos
x1= mean (energy); %m茅dia da energia
percentage = 100*energy/sum(energy);%energia em porcentagem
[maxpercent,maxScaleIDX] = max(percentage);%maxima porcentagem
r=thd(Swell_harmonic);
T9(i,:)={en1,en2,en3,x1,maxpercent,r,"swell_harmonic"};

[c1,c2] = dwt(Flicker,'dmey');% coeficientes discretos
en1 = wentropy(Flicker,'shannon');% entropia do sinal original
en2 = wentropy(c1,'shannon');% entropia dos coeficiente aproximados (approximation coefficients)
en3 = wentropy(c2,'shannon');% entropia dos coeficientes detalhados (detail coefficients)
% coeff = cwt(vwave); %coeficientes
energy = sqrt(sum(abs(c2).^2,2)); %energia dos coeficientes continuos
x1= mean (energy); %m茅dia da energia
percentage = 100*energy/sum(energy);%energia em porcentage

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]王继东,徐志林.基于DWT和极限学习机的电能质量扰动分类方法:CN201910819003.0[P].CN110610203A[2023-08-07].

[2]李令冬,朱明星,黄炜.智能电网的发展给电能质量研究与产业带来的机遇和挑战[C]//首届全国电能质量学术会议暨电能质量行业发展论坛.中国电源学会, 2009.

[3]Machine Learning Applications for a Robust Classifier of Advanced Power Quality Disturbances in Smart Grid", by Gabriel C. S. Almeida, at the Federal University of Itajubá.

🌈4 Matlab代码实现