卡尔曼滤波器的数学推导与应用实现
1. 引言
卡尔曼滤波器是一种强大的递归估计算法,广泛应用于信号处理、导航系统、控制理论、计算机视觉等领域。它通过融合预测模型和测量数据,在噪声环境下对系统状态进行最优估计。本文将详细推导卡尔曼滤波器的数学原理,并通过实例演示其在不同场景下的应用。

2. 基本原理与推导
2.1 预估值角度的推导
卡尔曼滤波的核心思想是将先验估计与实时测量数据进行融合,得到后验估计。我们首先从预估值角度出发进行推导。
对于系统模型:
x
^
k
=
F
k
x
^
k
−
1
+
B
k
u
k
+
w
k
\hat{x}_k = F_k\hat{x}_{k-1} + B_ku_k + w_k
x^k=Fkx^k−1+Bkuk+wk
其中测量方程为:
z
k
=
H
k
x
k
+
v
k
z_k = H_k x_k + v_k
zk=Hkxk+vk
忽略测量噪声
v
k
v_k
vk,可以得到:
z
k
≈
H
k
x
k
z_k \approx H_k x_k
zk≈Hkxk
这里
z
k
z_k
zk 是 k 时刻的测量值,通过观测值和观测矩阵,我们可以得到:
H
k
−
1
z
k
≈
x
k
H_k^{-1}z_k \approx x_k
Hk−1zk≈xk
我们通过观测值和观测矩阵获得了与预估值相同维度的量,将其与当前时刻通过过程模型得到的预测值作差,用来修正预测值的准确性:
x ^ k = x ^ k − + K k ( z k − H k x ^ k − ) \hat{x}_k = \hat{x}_k^- + K_k(z_k - H_k\hat{x}_k^-) x^k=x^k−+Kk(zk−Hkx^k−)
其中, K k K_k Kk 为系数矩阵(卡尔曼增益)。
本质上就是:
x
^
k
=
x
^
k
−
+
K
k
(
z
k
−
z
^
k
)
\hat{x}_k = \hat{x}_k^- + K_k(z_k - \hat{z}_k)
x^k=x^k−+Kk(zk−z^k)
此时有 z ^ k = H k x ^ k − \hat{z}_k = H_k\hat{x}_k^- z^k=Hkx^k−, x ^ k − \hat{x}_k^- x^k− 为先验估计值。
进一步简化,我们设:
x
^
k
=
x
^
k
−
+
K
k
(
z
k
−
H
k
x
^
k
−
)
\hat{x}_k = \hat{x}_k^- + K_k(z_k - H_k\hat{x}_k^-)
x^k=x^k−+Kk(zk−Hkx^k−)
其中, K k K_k Kk 为卡尔曼增益,当前为未知量。 x ^ k \hat{x}_k x^k 为最优值,由于和当前时刻的观测量有关系,也称为后验估计值。我们的目标是求解一个合适的 K k K_k Kk,使得最优估计值最接近真实值。
2.2 目标函数的建立与转化
将上述思路转化为数学语言,我们设 e k = x k − x ^ k e_k = x_k - \hat{x}_k ek=xk−x^k,即求解最优目标函数 min E [ e k T e k ] \min E[e_k^Te_k] minE[ekTek],其中 e k e_k ek 表示最优值和真实值的误差。
对于公式:
x
^
k
=
x
^
k
−
+
K
k
(
z
k
−
H
k
x
^
k
−
)
\hat{x}_k = \hat{x}_k^- + K_k(z_k - H_k\hat{x}_k^-)
x^k=x^k−+Kk(zk−Hkx^k−)
代入公式,并且为了构建
e
k
e_k
ek,我们使用
x
k
x_k
xk 分别减去左右两式,有:
e
k
=
x
k
−
x
^
k
=
x
k
−
x
^
k
−
−
K
k
(
z
k
−
H
k
x
^
k
−
)
e_k = x_k - \hat{x}_k = x_k - \hat{x}_k^- - K_k(z_k - H_k\hat{x}_k^-)
ek=xk−x^k=xk−x^k−−Kk(zk−Hkx^k−)
为了简化表示,我们设
e
k
−
=
x
k
−
x
^
k
−
e_k^- = x_k - \hat{x}_k^-
ek−=xk−x^k− 表示预测值和真实值的误差,则有:
e
k
=
e
k
−
−
K
k
(
H
k
x
k
+
v
k
−
H
k
x
^
k
−
)
=
e
k
−
−
K
k
H
k
e
k
−
−
K
k
v
k
=
(
I
−
K
k
H
k
)
e
k
−
−
K
k
v
k
\begin{align} e_k &= e_k^- - K_k(H_kx_k + v_k - H_k\hat{x}_k^-) \\ &= e_k^- - K_kH_ke_k^- - K_kv_k \\ &= (I - K_kH_k)e_k^- - K_kv_k \end{align}
ek=ek−−Kk(Hkxk+vk−Hkx^k−)=ek−−KkHkek−−Kkvk=(I−KkHk)ek−−Kkvk
直接通过随机变量的式求解最优目标函数显然不可行,我们通过表征随机变量的特征值来进行求解,最简单的特征值就是数学期望。不妨设:
P
k
=
E
[
e
k
e
k
T
]
P_k = E[e_ke_k^T]
Pk=E[ekekT] 表示的是真实值的最优值的后验误差协方差矩阵
P
k
−
=
E
[
e
k
−
(
e
k
−
)
T
]
P_k^- = E[e_k^-(e_k^-)^T]
Pk−=E[ek−(ek−)T] 表示的是真实值和预测值的先验误差协方差矩阵
根据
e
k
e_k
ek 的定义,我们不难得到:
P
k
=
E
[
e
k
e
k
T
]
=
E
[
(
x
k
−
x
^
k
)
(
x
k
−
x
^
k
)
T
]
P_k = E[e_ke_k^T] = E[(x_k - \hat{x}_k)(x_k - \hat{x}_k)^T]
Pk=E[ekekT]=E[(xk−x^k)(xk−x^k)T]
同理有 P k − = E [ ( x k − x ^ k − ) ( x k − x ^ k − ) T ] P_k^- = E[(x_k - \hat{x}_k^-)(x_k - \hat{x}_k^-)^T] Pk−=E[(xk−x^k−)(xk−x^k−)T],下文会利用该性质进行简化。
对于公式 e k = ( I − K k H k ) e k − − K k v k e_k = (I - K_kH_k)e_k^- - K_kv_k ek=(I−KkHk)ek−−Kkvk,两边分别乘以自己的转置,并取期望,来构造协方差矩阵,有:
P k = E [ e k e k T ] = E [ ( ( I − K k H k ) e k − − K k v k ) ( ( I − K k H k ) e k − − K k v k ) T ] \begin{align} P_k &= E[e_ke_k^T] \\ &= E[((I - K_kH_k)e_k^- - K_kv_k)((I - K_kH_k)e_k^- - K_kv_k)^T] \end{align} Pk=E[ekekT]=E[((I−KkHk)ek−−Kkvk)((I−KkHk)ek−−Kkvk)T]
由于测量噪声 v k v_k vk 和 e k − e_k^- ek−、 e k e_k ek、 x k x_k xk 无关,因此 v k v_k vk 和 e k − e_k^- ek−、 x k x_k xk 相互独立,考虑到 E [ v k ] = 0 E[v_k] = 0 E[vk]=0,则有:
P k = ( I − K k H k ) P k − ( I − K k H k ) T + K k R k K k T \begin{align} P_k &= (I - K_kH_k)P_k^-(I - K_kH_k)^T + K_kR_kK_k^T \end{align} Pk=(I−KkHk)Pk−(I−KkHk)T+KkRkKkT
其中 R k = E [ v k v k T ] R_k = E[v_kv_k^T] Rk=E[vkvkT] 是测量噪声的协方差矩阵。
因此,误差协方差矩阵可表示为:
P
k
=
(
I
−
K
k
H
k
)
P
k
−
(
I
−
K
k
H
k
)
T
+
K
k
R
k
K
k
T
P_k = (I - K_kH_k)P_k^-(I - K_kH_k)^T + K_kR_kK_k^T
Pk=(I−KkHk)Pk−(I−KkHk)T+KkRkKkT
至此,我们将随机变量的最优化问题转化成为了纯数量问题。
2.3 最优卡尔曼增益的求解
为了找到最优的卡尔曼增益 K k K_k Kk,我们需要最小化误差协方差矩阵 P k P_k Pk 的迹(trace)。迹表示的是主对角线元素之和,恰好为所有待估计量的方差之和。根据最小二乘法,最小化这个量可以得到最优解。
我们对 t r ( P k ) tr(P_k) tr(Pk) 关于 K k K_k Kk 求导,并使导数等于零:
∂ t r ( P k ) ∂ K k = 0 \frac{\partial tr(P_k)}{\partial K_k} = 0 ∂Kk∂tr(Pk)=0
首先,我们展开
P
k
P_k
Pk:
P
k
=
(
I
−
K
k
H
k
)
P
k
−
(
I
−
K
k
H
k
)
T
+
K
k
R
k
K
k
T
=
P
k
−
−
K
k
H
k
P
k
−
−
P
k
−
H
k
T
K
k
T
+
K
k
H
k
P
k
−
H
k
T
K
k
T
+
K
k
R
k
K
k
T
\begin{align} P_k &= (I - K_kH_k)P_k^-(I - K_kH_k)^T + K_kR_kK_k^T \\ &= P_k^- - K_kH_kP_k^- - P_k^-H_k^TK_k^T + K_kH_kP_k^-H_k^TK_k^T + K_kR_kK_k^T \end{align}
Pk=(I−KkHk)Pk−(I−KkHk)T+KkRkKkT=Pk−−KkHkPk−−Pk−HkTKkT+KkHkPk−HkTKkT+KkRkKkT
对此表达式的迹关于 K k K_k Kk 求导。使用矩阵求导的相关性质,我们得到:
∂ t r ( P k ) ∂ K k = − 2 ( H k P k − ) T + 2 K k H k P k − H k T + 2 K k R k = 0 \begin{align} \frac{\partial tr(P_k)}{\partial K_k} &= -2(H_kP_k^-)^T + 2K_kH_kP_k^-H_k^T + 2K_kR_k = 0 \end{align} ∂Kk∂tr(Pk)=−2(HkPk−)T+2KkHkPk−HkT+2KkRk=0
解得:
K
k
=
P
k
−
H
k
T
(
H
k
P
k
−
H
k
T
+
R
k
)
−
1
K_k = P_k^-H_k^T(H_kP_k^-H_k^T + R_k)^{-1}
Kk=Pk−HkT(HkPk−HkT+Rk)−1
这就是最优卡尔曼增益的表达式。
2.4 误差协方差矩阵的更新
将最优卡尔曼增益代入
P
k
P_k
Pk 的表达式,经过化简,可以得到:
P
k
=
(
I
−
K
k
H
k
)
P
k
−
P_k = (I - K_kH_k)P_k^-
Pk=(I−KkHk)Pk−
这是误差协方差矩阵更新的简化形式。
2.5 先验估计与先验误差协方差的预测
对于系统状态的预测,我们有:
x
^
k
−
=
F
k
−
1
x
^
k
−
1
+
B
k
−
1
u
k
−
1
\hat{x}_k^- = F_{k-1}\hat{x}_{k-1} + B_{k-1}u_{k-1}
x^k−=Fk−1x^k−1+Bk−1uk−1
为了构建先验误差
e
k
−
e_k^-
ek−,两边同时减去
x
k
x_k
xk,得到:
e
k
−
=
x
k
−
x
^
k
−
=
x
k
−
F
k
−
1
x
^
k
−
1
−
B
k
−
1
u
k
−
1
e_k^- = x_k - \hat{x}_k^- = x_k - F_{k-1}\hat{x}_{k-1} - B_{k-1}u_{k-1}
ek−=xk−x^k−=xk−Fk−1x^k−1−Bk−1uk−1
考虑到 x k = F k − 1 x k − 1 + B k − 1 u k − 1 + w k − 1 x_k = F_{k-1}x_{k-1} + B_{k-1}u_{k-1} + w_{k-1} xk=Fk−1xk−1+Bk−1uk−1+wk−1,其中 w k − 1 w_{k-1} wk−1 是过程噪声,我们有:
e k − = F k − 1 x k − 1 + B k − 1 u k − 1 + w k − 1 − F k − 1 x ^ k − 1 − B k − 1 u k − 1 = F k − 1 ( x k − 1 − x ^ k − 1 ) + w k − 1 = F k − 1 e k − 1 + w k − 1 \begin{align} e_k^- &= F_{k-1}x_{k-1} + B_{k-1}u_{k-1} + w_{k-1} - F_{k-1}\hat{x}_{k-1} - B_{k-1}u_{k-1} \\ &= F_{k-1}(x_{k-1} - \hat{x}_{k-1}) + w_{k-1} \\ &= F_{k-1}e_{k-1} + w_{k-1} \end{align} ek−=Fk−1xk−1+Bk−1uk−1+wk−1−Fk−1x^k−1−Bk−1uk−1=Fk−1(xk−1−x^k−1)+wk−1=Fk−1ek−1+wk−1
类似构建
P
k
P_k
Pk 的方式,我们构建先验误差协方差矩阵
P
k
−
P_k^-
Pk−。两边同时乘以自身的转置,考虑到
w
k
−
1
w_{k-1}
wk−1 和
e
k
−
1
e_{k-1}
ek−1 互相独立,有:
P
k
−
=
E
[
e
k
−
(
e
k
−
)
T
]
=
F
k
−
1
P
k
−
1
F
k
−
1
T
+
Q
k
−
1
P_k^- = E[e_k^-(e_k^-)^T] = F_{k-1}P_{k-1}F_{k-1}^T + Q_{k-1}
Pk−=E[ek−(ek−)T]=Fk−1Pk−1Fk−1T+Qk−1
其中 Q k − 1 = E [ w k − 1 w k − 1 T ] Q_{k-1} = E[w_{k-1}w_{k-1}^T] Qk−1=E[wk−1wk−1T] 是过程噪声的协方差矩阵。
3. 卡尔曼滤波算法总结
卡尔曼滤波算法包括两个主要步骤:预测步骤和更新步骤。
3.1 预测步骤
-
状态预测:
x ^ k − = F k − 1 x ^ k − 1 + B k − 1 u k − 1 \hat{x}_k^- = F_{k-1}\hat{x}_{k-1} + B_{k-1}u_{k-1} x^k−=Fk−1x^k−1+Bk−1uk−1 -
误差协方差预测:
P k − = F k − 1 P k − 1 F k − 1 T + Q k − 1 P_k^- = F_{k-1}P_{k-1}F_{k-1}^T + Q_{k-1} Pk−=Fk−1Pk−1Fk−1T+Qk−1
3.2 更新步骤
-
计算卡尔曼增益:
K k = P k − H k T ( H k P k − H k T + R k ) − 1 K_k = P_k^-H_k^T(H_kP_k^-H_k^T + R_k)^{-1} Kk=Pk−HkT(HkPk−HkT+Rk)−1 -
状态更新:
x ^ k = x ^ k − + K k ( z k − H k x ^ k − ) \hat{x}_k = \hat{x}_k^- + K_k(z_k - H_k\hat{x}_k^-) x^k=x^k−+Kk(zk−Hkx^k−) -
误差协方差更新:
P k = ( I − K k H k ) P k − P_k = (I - K_kH_k)P_k^- Pk=(I−KkHk)Pk−
4. 实现注意事项
在实际应用中,卡尔曼滤波器的实现需要注意以下几点:
-
初始化:需要设定初始状态估计 x ^ 0 \hat{x}_0 x^0 和初始误差协方差矩阵 P 0 P_0 P0。
-
矩阵求逆:在计算卡尔曼增益时,需要求逆矩阵 ( H k P k − H k T + R k ) − 1 (H_kP_k^-H_k^T + R_k)^{-1} (HkPk−HkT+Rk)−1。在实际编程中,应使用数值稳定的方法来计算逆矩阵,如LU分解或SVD分解。
-
数值稳定性:在长时间运行过程中,误差协方差矩阵 P k P_k Pk 可能会失去对称性或正定性,影响滤波器性能。一种常用的技巧是在每次更新后强制 P k P_k Pk 保持对称: P k = ( P k + P k T ) / 2 P_k = (P_k + P_k^T)/2 Pk=(Pk+PkT)/2。
-
模型参数设置:过程噪声协方差矩阵 Q k Q_k Qk 和测量噪声协方差矩阵 R k R_k Rk 的设置直接影响滤波器性能。这些参数通常需要根据实际系统特性进行调整。
-
非线性系统处理:对于非线性系统,可以使用扩展卡尔曼滤波器(EKF)或无迹卡尔曼滤波器(UKF)等变体算法。
5. 应用实例
5.1 追踪正弦函数
以下是使用卡尔曼滤波器追踪正弦函数的Python实现代码:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 卡尔曼滤波器追踪正弦函数
def track_sine_wave():
# 参数设置
dt = 0.1 # 时间步长
T = 10.0 # 总时间
N = int(T/dt) # 步数
t = np.linspace(0, T, N)
# 生成真实的正弦函数
frequency = 1.0 # Hz
amplitude = 1.0 # 幅度
true_signal = amplitude * np.sin(2 * np.pi * frequency * t)
# 添加高斯噪声的测量值
measurement_noise_std = 0.2
measurements = true_signal + np.random.normal(0, measurement_noise_std, N)
# 初始化卡尔曼滤波器
# 状态向量: [位置, 速度]
x = np.zeros((2, 1)) # 初始状态估计
P = np.diag([1.0, 1.0]) # 初始状态协方差
# 状态转移矩阵 (考虑速度)
F = np.array([[1, dt], [0, 1]])
# 过程噪声协方差
process_noise_std = 0.01
Q = np.array([[dt**4/4, dt**3/2], [dt**3/2, dt**2]]) * process_noise_std**2
# 测量矩阵 (只测量位置)
H = np.array([[1, 0]])
# 测量噪声协方差
R = np.array([[measurement_noise_std**2]])
# 存储估计结果
estimated_states = np.zeros((N, 2))
# 卡尔曼滤波
for k in range(N):
# 预测步骤
x = F @ x
P = F @ P @ F.T + Q
# 更新步骤
z = np.array([[measurements[k]]])
y = z - H @ x # 测量残差
S = H @ P @ H.T + R # 残差协方差
K = P @ H.T @ np.linalg.inv(S) # 卡尔曼增益
x = x + K @ y # 状态更新
P = (np.eye(2) - K @ H) @ P # 协方差更新
# 保存估计结果
estimated_states[k] = x.flatten()
# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(t, true_signal, 'g-', label='True Signal')
plt.plot(t, measurements, 'r.', label='Measurements')
plt.plot(t, estimated_states[:, 0], 'b-', label='Filtered Estimate')
plt.legend()
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Kalman Filter Tracking Sine Signal')
plt.grid(True)
plt.savefig('kalman_sine_tracking.png', dpi=300)
plt.show()
return estimated_states
# 执行追踪
if __name__ == "__main__":
estimated_states = track_sine_wave()
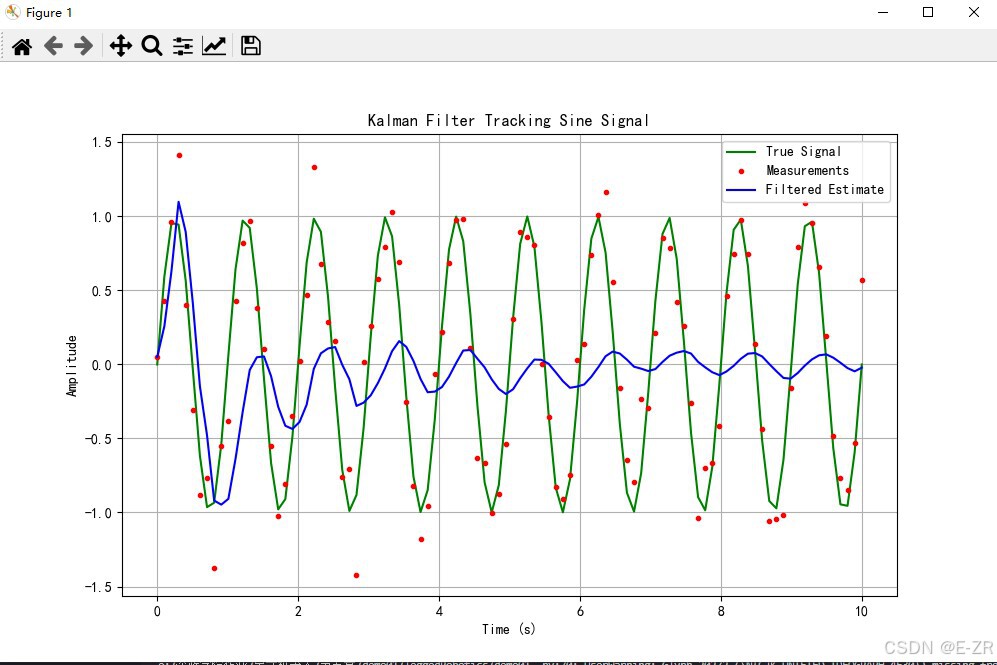
上述代码实现了卡尔曼滤波器追踪正弦函数的过程。滤波器使用二维状态向量表示位置和速度,仅观测位置值,并能有效地过滤掉测量噪声。下图显示了追踪效果:
5.2 追踪悬坠线函数(抛物线)
以下是使用卡尔曼滤波器追踪悬坠线(抛物线)的Python实现代码:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 卡尔曼滤波器追踪悬坠线(抛物线)
def track_catenary():
# 参数设置
dt = 0.1 # 时间步长
T = 10.0 # 总时间
N = int(T/dt) # 步数
t = np.linspace(-5, 5, N) # 从-5到5
# 生成真实的悬坠线(这里使用抛物线作为简化)
a = 0.5 # 系数
true_signal = a * t**2 # 抛物线: y = a*x^2
# 添加高斯噪声的测量值
measurement_noise_std = 0.5
measurements = true_signal + np.random.normal(0, measurement_noise_std, N)
# 初始化卡尔曼滤波器
# 状态向量: [位置, 速度, 加速度]
x = np.zeros((3, 1)) # 初始状态估计
P = np.diag([1.0, 1.0, 1.0]) # 初始状态协方差
# 状态转移矩阵 (考虑速度和加速度)
F = np.array([
[1, dt, dt**2/2],
[0, 1, dt],
[0, 0, 1]
])
# 过程噪声协方差
process_noise_std = 0.01
G = np.array([
[dt**3/6],
[dt**2/2],
[dt]
])
Q = G @ G.T * process_noise_std**2
# 测量矩阵 (只测量位置)
H = np.array([[1, 0, 0]])
# 测量噪声协方差
R = np.array([[measurement_noise_std**2]])
# 存储估计结果
estimated_states = np.zeros((N, 3))
# 卡尔曼滤波
for k in range(N):
# 预测步骤
x = F @ x
P = F @ P @ F.T + Q
# 更新步骤
z = np.array([[measurements[k]]])
y = z - H @ x # 测量残差
S = H @ P @ H.T + R # 残差协方差
K = P @ H.T @ np.linalg.inv(S) # 卡尔曼增益
x = x + K @ y # 状态更新
P = (np.eye(3) - K @ H) @ P # 协方差更新
# 保存估计结果
estimated_states[k] = x.flatten()
# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(t, true_signal, 'g-', label='True Signal')
plt.plot(t, measurements, 'r.', label='Measurements')
plt.plot(t, estimated_states[:, 0], 'b-', label='Filtered Estimate')
plt.legend()
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Kalman Filter Tracking Catenary (Parabola)')
plt.grid(True)
plt.savefig('kalman_catenary_tracking.png', dpi=300)
plt.show()
return estimated_states
# 执行追踪
if __name__ == "__main__":
estimated_states = track_catenary()
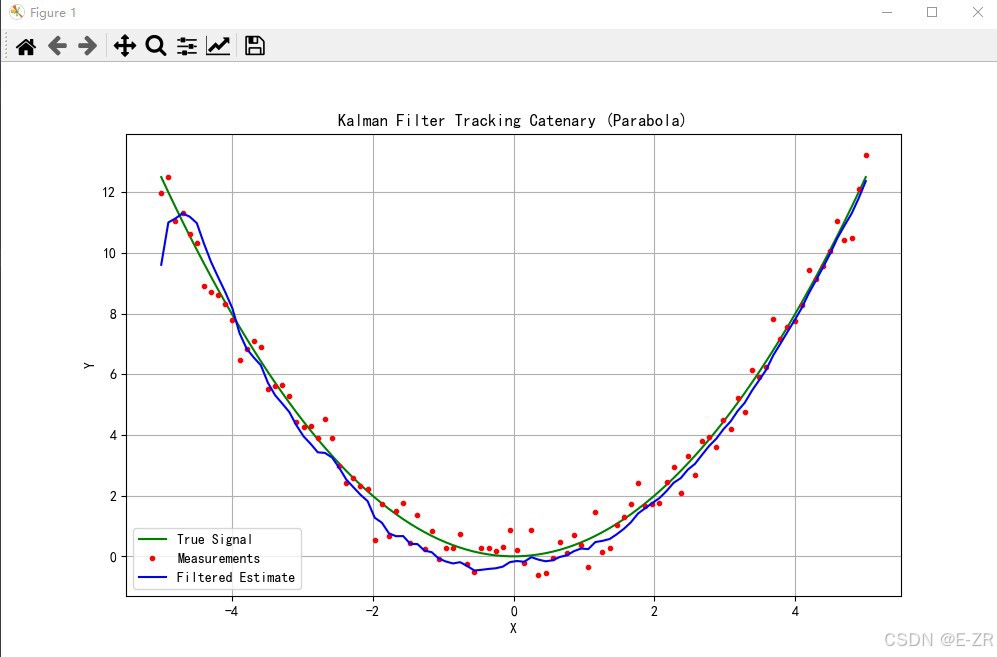
上述代码实现了卡尔曼滤波器追踪悬坠线(这里用抛物线近似)的过程。滤波器使用三维状态向量表示位置、速度和加速度,仅观测位置值。由于抛物线具有恒定的二阶导数,这种模型特别适合追踪二次函数。下图显示了追踪效果:
6. 结论与展望
本文从数学角度推导了卡尔曼滤波算法,包括最优卡尔曼增益的求解过程和误差协方差矩阵的更新方式。卡尔曼滤波器通过将预测模型与测量数据进行最优融合,能够在噪声环境下对系统状态进行准确估计。
同时也非常感谢DR_CAN博主的视频,让我熟悉卡尔曼滤波的公式,尝试自己理解的方式一步步推导公式,也感谢知乎NovemQi博主
附录:矩阵求导基础知识
在卡尔曼滤波推导过程中,我们用到了矩阵求导,特别是标量函数(迹)对矩阵的求导。下面列出一些重要结论:
-
∂ t r ( X ) ∂ X = I \frac{\partial tr(X)}{\partial X} = I ∂X∂tr(X)=I
-
∂ t r ( A X ) ∂ X = A T \frac{\partial tr(AX)}{\partial X} = A^T ∂X∂tr(AX)=AT
-
∂ t r ( X A ) ∂ X = A T \frac{\partial tr(XA)}{\partial X} = A^T ∂X∂tr(XA)=AT
-
∂ t r ( A X B ) ∂ X = A T B T \frac{\partial tr(AXB)}{\partial X} = A^TB^T ∂X∂tr(AXB)=ATBT
-
∂ t r ( A X T ) ∂ X = A \frac{\partial tr(AX^T)}{\partial X} = A ∂X∂tr(AXT)=A
-
∂ t r ( X A X T ) ∂ X = ( A X T + A T X T ) T = X ( A T + A ) = X ( A + A T ) \frac{\partial tr(XAX^T)}{\partial X} = (AX^T+A^TX^T)^T=X(A^T+A)=X(A+A^T) ∂X∂tr(XAXT)=(AXT+ATXT)T=X(AT+A)=X(A+AT)
-
∂ t r ( X T A X ) ∂ X = ( X T A + X T A T ) T = ( A T + A ) X = ( A T + A ) X \frac{\partial tr(X^TAX)}{\partial X} = (X^TA+X^TA^T)^T=(A^T+A)X=(A^T+A)X ∂X∂tr(XTAX)=(XTA+XTAT)T=(AT+A)X=(AT+A)X
-
∂ t r ( P ) ∂ X = ∂ t r ( P T ) ∂ X \frac{\partial tr(P)}{\partial X} = \frac{\partial tr(P^T)}{\partial X} ∂X∂tr(P)=∂X∂tr(PT)
这些性质在求解最优卡尔曼增益时非常有用。
参考文献
- Kalman, R. E. (1960). A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 82(1), 35-45.
- Simon, D. (2006). Optimal state estimation: Kalman, H infinity, and nonlinear approaches. John Wiley & Sons.
- Grewal, M. S., & Andrews, A. P. (2014). Kalman filtering: Theory and practice with MATLAB. Wiley-IEEE Press.
- 卡尔曼滤波五个公式各个参数的意义_卡尔曼滤波公式参数含义-CSDN博客
- 【卡尔曼滤波器】4_误差协方差矩阵数学推导_卡尔曼滤波器的五个公式_哔哩哔哩_bilibili
- 方差计算公式_百度百科























 803
803

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








