1、验证旋转矩阵是正交矩阵。
旋转矩阵(Rotate Matrix)的性质分析:该博客对于正交矩阵的性质做了良好叙述,在此引用此博客,不在过多赘述。
2、罗德里格斯公式的推导。
由于笔者查找的罗德里格斯公式的推导,符号都比较混乱,笔者重新书写一遍仅供参考。


笔者字迹实在潦草,感谢某只郭的誊抄。
3、验证四元数旋转某个点后,结果是一个虚四元数。
四元数旋转运算过程:该博客对于此题目做了良好叙述,在此引用此博客,不在过多赘述。
4、画表总结旋转矩阵、轴角、欧拉角、四元数的转换关系。
旋转矩阵、欧拉角、四元数、轴/角之间的转换:该博客对于此题目做了良好叙述,在此引用此博客,不在过多赘述。
5、假设有一个大的 Eigen矩阵,想把它的左上角3x3的块取出来,然后赋值为I3x3。请编写代码。
本题采用两种方法进行解答:
- 循环访问
- 使用.block()。
.block()块表达式既可以用作右值,也可以用作左值。具体操作请查看代码注释或者参考Eigen-Block块操作
Code
#include<iostream>
//包含Eigen头文件
#include<Eigen/Core>//Eigen核心模块
#include<Eigen/Geometry>//Eigen几何模块
#define MATRIX_SIZE 30//定义矩阵的大小
using namespace std;
int main(int argc,char **argv)
{
//设置输出小数点后3位
cout.precision(3);
Eigen::Matrix<double,MATRIX_SIZE, MATRIX_SIZE> matrix_NN = Eigen::MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);//生成随机数矩阵
Eigen::Matrix<double,3,3>matrix_3d1 = Eigen::MatrixXd::Random(3,3);//3x3矩阵变量
Eigen::Matrix3d matrix_3d = Eigen::Matrix3d::Random();//两种方式都可以
/*方法1:循环遍历矩阵的三行三列 */
for(int i = 0;i < 3; i ++)
{
for(int j = 0 ;j < 3;j++)
{
matrix_3d(i,j) = matrix_NN(i,j);
cout<<matrix_NN(i,j)<<" ";
}
cout<<endl;
}
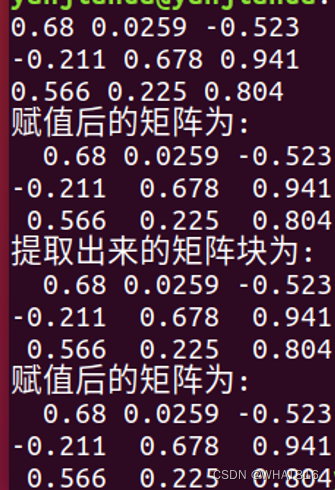
cout<<"赋值后的矩阵为:"<<endl<<matrix_3d<<endl;
//方法2:用.block函数
/*Eigen中最通用的块操作称为.block()。有两个版本,语法如下:
| 块操作 | 动态大小的块表达式 | 固定大小块表达式
|大小为(p, q)的块,从(i, j)开始 | matrix.block(i, j, p, q); | matrix.block < p, q >(i, j);*/
/*这两个版本都可以用于固定大小和动态大小的矩阵和数组。
这两个表达式在语义上是等价的。
唯一的区别是,如果块大小很小,固定大小的版本通常会提供更快的代码,
但需要在编译时知道这个大小。
块表达式既可以用作右值,也可以用作左值
*/
cout<<"提取出来的矩阵块为:"<<endl;
cout<< matrix_NN.block(0,0,3,3) <<endl;//matrix.block(i,j,p,q) 提取块大小为(p,q),起始于(i,j)
//提取后赋值为新的元素
matrix_3d = matrix_NN.block(0,0,3,3);
cout<<"赋值后的矩阵为:"<<endl<<matrix_3d;
return 0;
}
CMake
cmake_minimum_required(VERSION 2.8)
project(Test)
set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")
# 添加Eigen头文件
include_directories("/usr/include/eigen3")
add_executable(TestBlock TestBlock.cpp)运行结果:
6、一般线性方程 Ax =b有哪几种做法?你能在 Eigen 中实现吗?
求解Ax=b有多种方法,本文介绍并采用Eigen展示常见的几种,例如Cholesky分解、SVD分解、LU分解、QR分解,雅克比(Jacobi)迭代法求解线性方程组。
Ax=b求解条件:
1、m < n, 欠定方程,有无穷多解
2、m = n,A非奇异,有唯一解;不可逆,无穷解或无解
3、m > n,超定方程,没有精确解,只有最小二乘解(Cholesky 分解、SVD分解、LU分解、QR分解),QR比SVD快,但SVD更准确。
本文仅采用Eigen方法进行测试,具体数学原理请参考YcoFlegs博主、兔子不吃草~博主的解答。
Eigen中的求解方法:

Note:
1.从速度上来看,Cholesky分解方法速度是最快的,并且精度较好,但其要求矩阵A是对称正定的;
2.精度最好最稳定的是SVD分解法,但求解速度慢;
3.LU分解和QR分解速度和精确性居中,但其要求矩阵A是满秩的。
上述Eigen分析参考了Ax=b常见解法对比
此外也可采用雅克比(Jacobi)迭代法求解线性方程组:
迭代法常用于求解大型稀疏矩阵,否则迭代法相较于直接法就没了优势;
迭代法适用于三对角方程组;
迭代法数学原理分析请参考:雅克比(Jacobi)迭代法求解线性方程组
Code
#include <iostream>
#include <ctime>
#include <cmath>
#include <complex>
/*线性方程组Ax = b的解法(直接法(1,2,3,4,5,6)+迭代法(7))
其中只有2 3 6方法不要求方程组个数与变量个数相等*/
#include <Eigen/Dense>
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <Eigen/Eigenvalues>
#define MATRIX_SIZE 3
#define MATRIX_SIZE_ 3
using namespace std;
typedef Eigen::Matrix<double, MATRIX_SIZE, MATRIX_SIZE_> Mat_A;
typedef Eigen::Matrix<double, MATRIX_SIZE, 1> Mat_B;
double Jacobi_sum(Mat_A& A, Mat_B& B, int i);
Mat_B Jacobi(Mat_A &A,Mat_B &b, int &iteration_num, double &accuracy );
int main(int argc, char** argv)
{
//设置输出小数点后3位
cout.precision(3);
//初始化A 与 b;
Mat_A matrix_NN = Eigen::MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE_);
Mat_B v_Nd = Eigen::MatrixXd::Random(MATRIX_SIZE, 1);
//测试用例
matrix_NN << 10,3,1,2,-10,3,1,3,10;//测试所用矩阵A
v_Nd <<14,-5,14;//测试所用向量b
Mat_B x;
clock_t tim_stt = clock();
/*1、求逆法 很可能没有解 仅仅针对可逆矩阵A才能计算*/
#if (MATRIX_SIZE == MATRIX_SIZE_)
x = matrix_NN.inverse() * v_Nd; // x = A(-1)b
std::cout<<"直接法所用时间和解为:"<< 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
<<"MS"<< std::endl << x.transpose() << std::endl;
#endif
/*2、QR分解解方程组 适合非方阵和方阵 当方程组有解时的出的是真解,
若方程组无解得出的是近似解*/
tim_stt = clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
std::cout<<"QR分解所用时间和解为:"<<1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
<< "MS" << std::endl << x.transpose() << std::endl;
/*3、最小二乘法 适合非方阵和方阵,方程组有解时得出真解,
否则是最小二乘解(在求解过程中可以用QR分解 分解最小二成的系数矩阵) */
tim_stt = clock();
//x=(A(T) * A)(-1) *( A(T) * b)
x = (matrix_NN.transpose() * matrix_NN).inverse() * (matrix_NN.transpose() * v_Nd);
std::cout<<"最小二乘法所用时间和解为:"<< 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
<< "MS" << std::endl << x.transpose() << std::endl;
/*4、LU分解方法 只能为方阵(满足分解的条件才行) */
#if (MATRIX_SIZE == MATRIX_SIZE_)
tim_stt = clock();
x = matrix_NN.lu().solve(v_Nd);//LU分解matrix_NN.lu()
std::cout<< "LU分解方法所用时间和解为:" << 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
<< "MS" << std::endl << x.transpose() << std::endl;
#else
std::cout<<"LU分解法不能解!(提示:直接法中方程组的个数必须与变量个数相同,需要设置MATRIX_SIZE == MATRIX_SIZE_)"<<std::endl;
#endif
/*5、Cholesky 分解方法 只能为方阵 (结果与其他的方法差好多)*/
#if (MATRIX_SIZE == MATRIX_SIZE_)
tim_stt = clock();
x = matrix_NN.llt().solve(v_Nd);//Cholesky分解matrix_NN.llt()
std::cout<< "Cholesky 分解方法所用时间和解为:" << 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
<< "MS"<< std::endl<< x.transpose()<<std::endl;
#endif
/*SVD分解法,适合非方阵和方阵 (结果与其他的方法差好多)*/
tim_stt = clock();
x = matrix_NN.jacobiSvd().solve(v_Nd);
std::cout<< "SVD_jacobi分解方法所用时间和解为:" << 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
<< "MS"<< std::endl<< x.transpose()<<std::endl;
tim_stt = clock();
x = matrix_NN.bdcSvd().solve(v_Nd);
std::cout<< "SVD_bdc分解方法所用时间和解为:" << 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
<< "MS"<< std::endl<< x.transpose()<<std::endl;
/*7、Jacobi迭代法 */
#if (MATRIX_SIZE == MATRIX_SIZE_)
int Iteration_num = 10 ;//迭代次数
double Accuracy =0.01;//精度
tim_stt = clock();
x= Jacobi(matrix_NN,v_Nd,Iteration_num,Accuracy);
std::cout<< "Jacobi 迭代法所用时间和解为:" << 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
<< "MS"<< std::endl<< x.transpose()<<std::endl;
#else
std::cout<<"Jacobi迭代法不能解!(提示:直接法中方程组的个数必须与变量个数相同,需要设置MATRIX_SIZE == MATRIX_SIZE_)"<<std::endl;
#endif
return 0;
}
//迭代不收敛的话 解向量是0
Mat_B Jacobi(Mat_A &A,Mat_B &b, int &iteration_num, double &accuracy ) {
Mat_B x_k = Eigen::MatrixXd::Zero(MATRIX_SIZE_,1);//迭代的初始值
Mat_B x_k1; //迭代一次的解向量
int k,i; //i,k是迭代算法的循环次数的临时变量
double temp; //每迭代一次解向量的每一维变化的模值
double R=0; //迭代一次后,解向量每一维变化的模的最大值
int isFlag = 0; //迭代要求的次数后,是否满足精度要求
//判断Jacobi是否收敛
Mat_A D; //D矩阵
Mat_A L_U; //L+U
Mat_A temp2 = A; //临时矩阵获得A矩阵除去对角线后的矩阵
Mat_A B; //Jacobi算法的迭代矩阵
Eigen::MatrixXcd EV;//获取矩阵特征值
double maxev=0.0; //最大模的特征值
int flag = 0; //判断迭代算法是否收敛的标志 1表示Jacobi算法不一定能收敛到真值
std::cout<<std::endl<<"欢迎进入Jacobi迭代算法!"<<std::endl;
//對A矩陣進行分解 求取迭代矩陣 再次求取譜半徑 判斷Jacobi迭代算法是否收斂
for(int l=0 ;l < MATRIX_SIZE;l++){
D(l,l) = A(l,l);
temp2(l,l) = 0;
if(D(l,l) == 0){
std::cout<<"迭代矩阵不可求"<<std::endl;
flag =1;
break;
}
}
L_U = -temp2;
B = D.inverse()*L_U;
//求取特征值
Eigen::EigenSolver<Mat_A>es(B);
EV = es.eigenvalues();
// cout<<"迭代矩阵特征值为:"<<EV << endl;
//求取矩陣的特征值 然後獲取模最大的特徵值 即爲譜半徑
for(int index = 0;index< MATRIX_SIZE;index++){
maxev = ( maxev > __complex_abs(EV(index)) )?maxev:(__complex_abs(EV(index)));
}
std::cout<< "Jacobi迭代矩阵的谱半径为:"<< maxev<<std::endl;
//谱半径大于1 迭代法则发散
if(maxev >= 1){
std::cout<<"Jacobi迭代算法不收敛!"<<std::endl;
flag =1;
}
//迭代法收敛则进行迭代的计算
if (flag == 0 ){
std::cout<<"Jacobi迭代算法谱半径小于1,该算法收敛"<<std::endl;
std::cout<<"Jacobi迭代法迭代次数和精度: "<< std::endl << iteration_num<<" "<<accuracy<<std::endl;
//迭代计算
for( k = 0 ;k < iteration_num ; k++ ){
for(i = 0;i< MATRIX_SIZE_ ; i++){
x_k1(i) = x_k(i) + ( b(i) - Jacobi_sum(A,x_k,i) )/A(i,i);
temp = fabs( x_k1(i) - x_k(i) );
if( fabs( x_k1(i) - x_k(i) ) > R )
R = temp;
}
//判断进度是否达到精度要求 达到进度要求后 自动退出
if( R < accuracy ){
std::cout <<"Jacobi迭代算法迭代"<< k << "次达到精度要求."<< std::endl;
isFlag = 1;
break;
}
//清零R,交换迭代解
R = 0;
x_k = x_k1;
}
if( !isFlag )
std::cout << std::endl <<"迭代"<<iteration_num<<"次后仍然未达到精度要求,若不满意该解,请再次运行加大循环次数!"<< std::endl;
return x_k1;
}
//否则返回0
return x_k;
}
//Jacobi迭代法的一步求和计算
double Jacobi_sum(Mat_A &A,Mat_B &x_k,int i) {
double sum;
for(int j = 0; j< MATRIX_SIZE_;j++){
sum += A(i,j)*x_k(j);
}
return sum;
}
该代码参考了博客视觉slam十四讲课后习题ch3-6
CMake
cmake_minimum_required(VERSION 2.8)
project(homework1)
set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")
# 添加Eigen头文件
include_directories("/usr/include/eigen3")
add_executable(TestAbX TestAbX.cpp)运行结果:
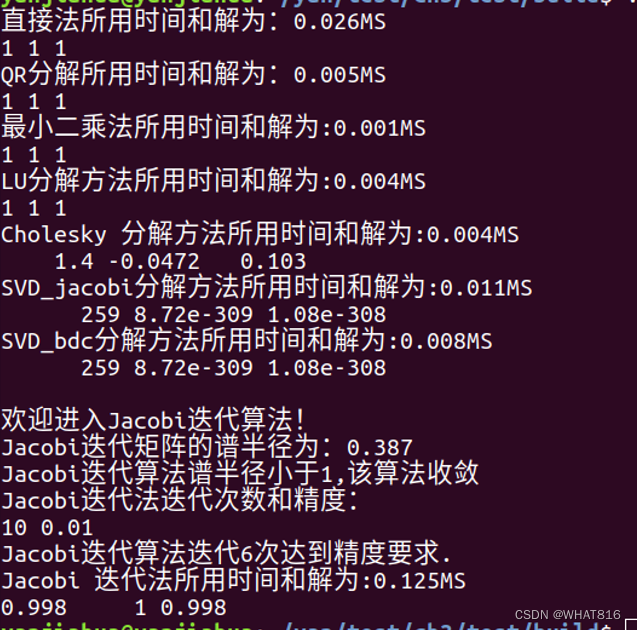
可见各算法与上述分析耗时一致,但SVD分解法、Cholesky分解法 结果与其他的方法差距较大。具体原因仍在思考,大佬经过请指教。






















 8454
8454











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








