【LDA 01篇】图解LDA原理

代码江

已于 2024-12-27 12:04:26 修改

阅读量2.4k

点赞数 25

文章标签：机器学习人工智能

于 2024-12-27 12:02:30 首次发布

本文链接：https://blog.csdn.net/weixin_71246590/article/details/144349548

版权

前言：

该篇主要讲述了LDA原理，主要内容参考以下链接里的视频p1。

LDA主题模型_哔哩哔哩_bilibili

不涉及复杂的公式推理，尽量用大白话讲明白LDA的基础原理。

一、LDA基础

1.1 背景（所解决的问题）：

我们有一堆新闻，我们不知道每篇新闻是什么主题的，每篇新闻都有一个或几个主题。我们可以人工阅读每篇文章，去分类主题，但是这样太麻烦了，效率很低。我们希望有个算法，帮助我们将这些文档自动分类主题，并且分析出每个主题的关键词。

1.2 什么是LDA 及其作用？

LDA（Latent Dirichlet Allocation）是一种主题模型，常用于文本分析中，用来从大量文档中发现潜在的主题。

核心功能：

文档-主题分布：每篇文档会根据内容分布到不同的主题。

主题-词分布：每个主题对应一定的关键词，表示主题的含义。

1.3 LDA模型：

这是出现在大多数文献中的LDA蓝图：

文献中经常出现的是这个公式：

这个公式看起来很复杂，大家不要被劝退，后面我会逐一讲解。

二、图解LDA理论

2.1 把LDA比作一个机器

把LDA比作一个机器，按下按钮会生成一篇文章，

文章可能是胡言乱语的一堆单词，也有可能是一篇奇怪的文章。特别小的概率会得到原始的文章。

寻找机器最好的“设置”

假设我们有两个机器，生成了两篇文章，我们比较它与真文章比较。

哪个机器能生产更像原文的文章，就说明它有更好的设置。

重要的是，我们会有大量的机器，就能找到最好的设置。

而这些设置就是我们在寻找的主题分布。

2.2 机器是怎么随机生成文档的呢？

我们先来讲解机器设置的参数这一部分

文档-主题分布 θ： 每个文档是由不同主题的概率组合生成的，θ 从狄利克雷分布（参数为 α）中采样。
主题-词分布 ϕ： 每个主题是由不同词的概率组合生成的，ϕ从狄利克雷分布（参数为 β）中采样。

什么是狄利克雷分布？

将狄利克雷分布看做一个派对，假设我们有一个三角形的房子，黄色圆点是排队中的人，在party中，人们可以自由的在房子漫游，这意味着房子里找到每个人的概率都是相同的。

当我们在不同的角布置上不同的东西时，一些人选择去干饭，一些人选择去听音乐，一些人选择既听音乐又干饭，很少人会选择什么都不去。

因此在角落找到点的概率很大，因此在中心的人很少。

如图，我们在每个角放上一些危险的事务时，人们会倾向于中心。

那么此时在中心找到点的概率高于在角落里的。

这样的现象就类似狄利克雷分布。

狄利克雷分布性质：

在狄利克雷分布中，

当 $\alpha$ =1时，点均匀分布，

当 $\alpha$ <1时，点往往会分布在角落附近，

当 $\alpha$ >1时，点会聚到中间。

我们可以看到不同的参数，所对应的狄利克雷分布的概率密度不一样。

那么，主题-文章的狄利克雷分布 $\alpha$ 应该是下图哪一种呢？

答案是中间这种，因为如果你拿一篇文章，它的主题可能是sports 或者 science 或者 politics，不太可能是他们三个，小概率是两个主题。

第一个狄利克雷分布 $\alpha$ ：

详细讲讲这个分布：

每篇文档都有一个对应的主题分布，可以想象成每个主题都是三种颜色的结合，只是不同颜色的占比不一样。

当我们的主题数量不是3时呢？

主题数为2时，我们将它放在一个线段上，两个端点代表主题。

主题数为3时，我们将它放在等边三角形里。

主题数为4时，我们将它放在正四面体里。（而不是正方形，因为正方形不能保证每个端点之间的距离相等）

......

后面我们将会还画出n维单形，我们会在越来越高的维度上绘制单形。

狄利克雷分布可以存在于任何维度。

第二个狄利克雷分布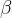 $\beta$ ：

假设我们有一个主题topic：science（科学），我们会将它放在这个由所有单词组成的正四面体的哪里呢？

我想我应该会放在planet（星球）和galaxy（银河）之间。

我们对所有主题进行一次该操作

我们得到第二个狄利克雷的分布 $\beta$ 。

总结一下：

我们有两个狄利克雷分布，

左边的：可以得到每篇文档对应哪些主题~

右边的：可以得到每个主题分别对应哪些单词~

这两个分布就是机器的设置，齿轮将会根据这些设置来生成文章。

两个狄利克雷分布联系起来：

现在来看看他们怎么联系起来 ~

如图，在文档-主题分布中，随机选取一个点，得到其主题分布。

再根据其分布，得到一个多项式概率模型。

再从多项式概率模型中抽取小球，

我们得到了了组成文章的单词的主题。

我们得到了组成文章的单词的主题，现在要根据这些主题找单词，

为此，我们使用第二个狄利克雷分布：主题-词分布，该分布连接了主题和单词！

如图，我们根据第二个狄利克雷分布：主题-词分布，制作关于每个主题的对应单词抽奖盒。

现在我们使用这些箱子把主题和单词联系起来：

先从主题盒子里抽出一个带颜色的小球（主题），

再从再从对应颜色的词盒里抽出单词~

如图，先抽到了主题science，再在science盒子里抽出了planet。

重复这个过程，得到下图：

我们得到了一篇“文档”。

我们选择黄色的点作为文章，选择红绿蓝的点作为主题，生成一堆文档。

我们回头检查他们是否与开始的文档相同，这些文章，对应左边每个黄点的分布，他们是根据黄点的位置生成的，现在得到相同文章的概率非常低。

虽然得到相同的文章概率是很低的，但是当我们有不同文档-主题排列，和不同的主题-单词排列时，每次组合得到的概率都是不一样的。

此时，概率相对较高的就胜出了，这个设置返回正确文档的概率较高，因为它的文档处于正确的主题分布中，主题处于正确的单词分布中。

三、总结

梳理理论：

LDA可以看做一台机器，上面的设置是狄利克雷分布，机器上的齿轮就是多项式分布，这些分布来自于设置的狄利克雷分布。

我们比较不同设置的机器，找出那个最有可能给我们原始文档的最佳设置。

先看黄点的位置：可以得到每篇文档的主题分布

查看右侧分布绿蓝黄小点的位置：可以得到每个主题相关性强的单词集，我们再根据单词集判断出主题是什么（这一步人为判断。）

再看机器蓝图：

- $\alpha$ 代表第一个文档-主题的狄利克雷分布，

- $\beta$ 代表主题-单词的狄利克雷分布，

- 从 $\alpha$ 中得到 $\theta$ （多项式分布），从 $\theta$ 中得到主题Z，

- 从 $\beta$ 中得到 $\phi$ （一系列多项式分布），从 $\phi$ 中可以得到单词，联合Z和 $\phi$ ，得到一系列单词，连接这些单词得到一篇文档，重复多次，生成语料库中的大量文档，之后与原始文档进行比较，找出狄利克雷分布中点的最佳分布方式，从而最大化概率。