1.LDA贝叶斯模型
LDA是基于贝叶斯模型的,涉及到贝叶斯模型离不开“先验分布”,“数据(似然)”和"后验分布"三块。其中:
先验分布 + 数据(似然)= 后验分布
先验分布为:100个好人和100个的坏人,即认为好人坏人各占一半,现在如果你被2个好人(数据)帮助了和1个坏人骗了,于是你得到了新的后验分布为:102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布,当你被1个好人(数据)帮助了和3个坏人(数据)骗了后,你又更新了你的后验分布为:103个好人和104个的坏人。依次继续更新下去。
2. 二项分布与Beta分布
用数学和概率的方式来表达贝叶斯模型:
对于数据(似然),用二项分布来表达:
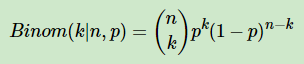
其中p我们可以理解为好人的概率,k为好人的个数,n为好人坏人的总数
因为我们希望这个先验分布和数据(似然)对应的二项分布集合后,得到的后验分布在后面还可以作为先验分布,也就是说,我们希望先验分布和后验分布的形式应该是一样的,这样的分布一般叫共轭分布。在我们的例子里,我们应该找到和二项分布共轭的分布。
和二项分布共轭的分布是Beta分布。Beta分布的表达式为:
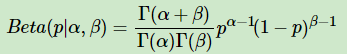
其中Γ是Gamma函数,满足Γ(x)=(x−1)!
Beta分布和二项分布,可以发现两者的密度函数很相似,区别仅仅在前面的归一化的阶乘项。在该情况下,后验分布的推导如下:
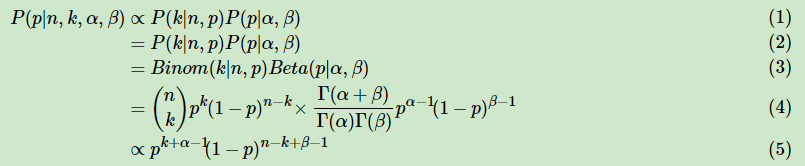
将上面最后的式子归一化以后,得到的后验概率为

可见我们的后验分布的确是Beta分布,同时发现:
![]()
符合一开始的预想
同时,求出Beta分布的期望:

由于上式最右边的乘积对应Beta分布Beta(p|α+1,β)因此有:

这样Beta分布的期望可以表达为:

也符合一开始的思路。
3. 多项分布与Dirichlet 分布
在文本识别过程中,不止是简单的好人与坏人的区分,同时可能还会有不好不坏的人,那么之前是二维分布,现在成了三维分布,由于二维我们使用了Beta分布和二项分布来表达这个模型,则在三维时,以此类推,我们可以用三维的Beta分布来表达先验后验分布,三项的多项分布来表达数据(似然)。
三项的多项分布好表达,我们假设数据中的第一类有m1个好人,第二类有m2个坏人,第三类为m3=n−m1−m2个不好不坏的人,对应的概率分别为p1,p2,p3=1−p1−p2则对应的多项分布为:
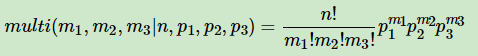
超过二维的Beta分布我们一般称之为狄利克雷(以下称为Dirichlet )分布。也可以说Beta分布是Dirichlet 分布在二维时的特殊形式。那么三维的Dirichlet分布如下:

同样的方法,我们可以写出4维,5维,。。。以及更高维的Dirichlet 分布的概率密度函数。为了简化表达式,我们用向量来表示概率和计数,这样多项分布可以表示为:Dirichlet( |
),而多项分布可以表示为:multi(
|
,
)。
一般意义上的K维Dirichlet 分布表达式为:

而多项分布和Dirichlet 分布也满足共轭关系,这样我们可以得到和上一节类似的结论:
![]()
对于Dirichlet 分布的期望,也有和Beta分布类似的性质:
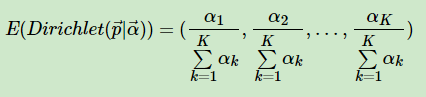
4. LDA主题模型
我们的问题是这样的,我们有M篇文档,对应第d个文档中有有Nd个词。即输入为如下图:

我们的目标是找到每一篇文档的主题分布和每一个主题中词的分布。在LDA模型中,我们需要先假定一个主题数目K,这样所有的分布就都基于K个主题展开。那么具体LDA模型如下图:

描述流程为:
从狄利克雷分布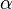
从主题的多项式分布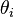
从狄利克雷分布 中取样生成主题
对应的词语分布
从词语的多项式分布中采样最终生成词语
LDA假设文档主题的先验分布是Dirichlet分布,即对于任一文档d, 其主题分布为:
![]()
其中,α为分布的超参数,是一个K维向量。
LDA假设主题中词的先验分布是Dirichlet分布,即对于任一主题k, 其词分布为:
![]()
其中,η为分布的超参数,是一个V维向量。V代表词汇表里所有词的个数。
对于数据中任一一篇文档d中的第n个词,我们可以从主题分布中得到它的主题编号
的分布为:
![]()
而对于该主题编号,得到我们看到的词的概率分布为:
![]()
这个模型里,我们有M个文档主题的Dirichlet分布,而对应的数据有M个主题编号的多项分布,这样(α→→
)就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。
如果在第k个主题中,第v个词的个数为:, 则对应的多项分布的计数可以表示为
![]()
利用Dirichlet-multi共轭,得到θd的后验分布为:
![]()
同样的道理,对于主题与词的分布,我们有K个主题与词的Dirichlet分布,而对应的数据有K个主题编号的多项分布,这样( →
→
)就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。
如果在第k个主题中,第v个词的个数为:, 则对应的多项分布的计数可以表示为
![]()
利用Dirichlet-multi共轭,得到的后验分布为:
![]()
5. 变分推断EM算法求解LDA的思路
首先,回顾LDA的模型图如下:
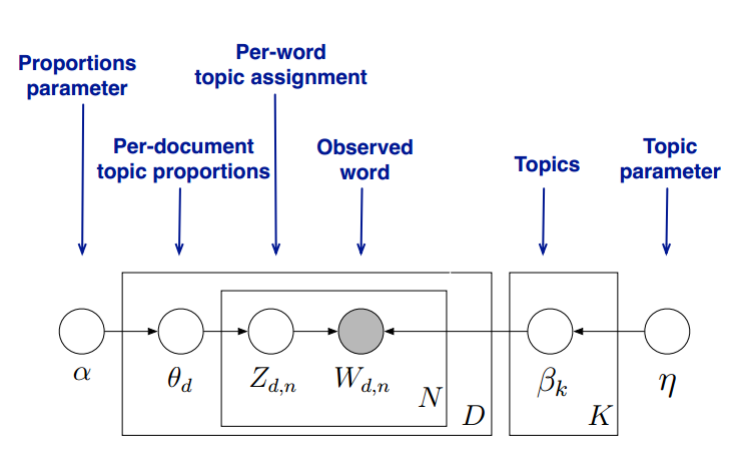
变分推断EM算法希望通过“变分推断(Variational Inference)”和EM算法来得到LDA模型的文档主题分布和主题词分布。首先来看EM算法在这里的使用,我们的模型里面有隐藏变量θ,β,z,模型的参数是α,η。为了求出模型参数和对应的隐藏变量分布,EM算法需要在E步先求出隐藏变量θ,β,z的基于条件概率分布的期望,接着在M步极大化这个期望,得到更新的后验模型参数α,η。
问题是在EM算法的E步,由于θ,β,z的耦合,我们难以求出隐藏变量θ,β,z的条件概率分布,也难以求出对应的期望,需要“变分推断“来帮忙,这里所谓的变分推断,也就是在隐藏变量存在耦合的情况下,我们通过变分假设,即假设所有的隐藏变量都是通过各自的独立分布形成的,这样就去掉了隐藏变量之间的耦合关系。我们用各个独立分布形成的变分分布来模拟近似隐藏变量的条件分布,这样就可以顺利的使用EM算法了。
当进行若干轮的E步和M步的迭代更新之后,我们可以得到合适的近似隐藏变量分布θ,β,z和模型后验参数α,η,进而就得到了我们需要的LDA文档主题分布和主题词分布。
要使用EM算法,我们需要求出隐藏变量的条件概率分布如下:
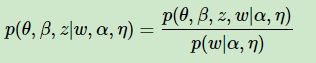
由于θ,β,zθ,β,z之间的耦合,这个条件概率是没法直接求的,于是我们引入变分推断,这个推断假设所有的隐藏变量都是通过各自的独立分布形成的,如下图所示:
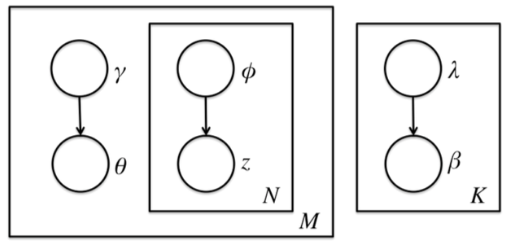
我们假设隐藏变量θ是由独立分布γ形成的,隐藏变量z是由独立分布ϕ形成的,隐藏变量β是由独立分布λ形成的。这样我们得到了三个隐藏变量联合的变分分布q为:
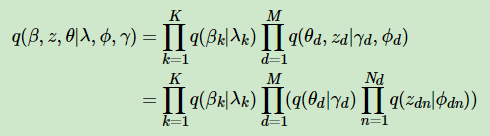
我们的目标是用q(β,z,θ|λ,ϕ,γ)来近似的估计p(θ,β,z|w,α,η),也就是说需要这两个分布尽可能的相似,用数学语言来描述就是希望这两个概率分布之间有尽可能小的KL距离,即:
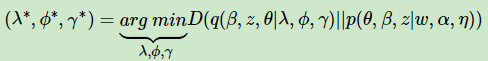
其中D(q||p)即为KL散度或KL距离,对应分布q和p的交叉熵。即:
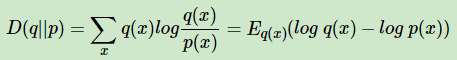
我们的目的就是找到合适的λ∗,ϕ∗,γ∗,然后用q(β,z,θ|λ∗,ϕ∗,γ∗)来近似隐藏变量的条件分布p(θ,β,z|w,α,η),进而使用EM算法迭代。
我们先看看我能文档数据的对数似然函数log(w|α,η)如下,为了简化表示,我们用Eq(x)代替Eq(β,z,θ|λ,ϕ,γ)(x),用来表示x对于变分分布q(β,z,θ|λ,ϕ,γ)的期望。

其中,从第(5)式到第(6)式用到了Jensen不等式:
![]()
把第(7)式记为:
![]()
由于L(λ,ϕ,γ;α,η)是我们的对数似然的一个下界(第6式),所以这个L一般称ELBO(Evidence Lower BOund)。那么这个ELBO和我们需要优化的的KL散度的关系如下: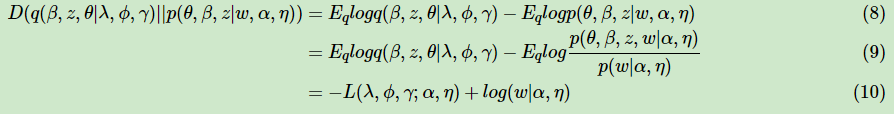
在(10)式中,由于对数似然部分和我们的KL散度无关,可以看做常量,因此我们希望最小化KL散度等价于最大化ELBO。那么我们的变分推断最终等价的转化为要求ELBO的最大值。现在我们开始关注于极大化ELBO并求出极值对应的变分参数λ,ϕ,γ。
极大化ELBO求解变分参数
为了极大化ELBO,我们首先对ELBO函数做一个整理如下
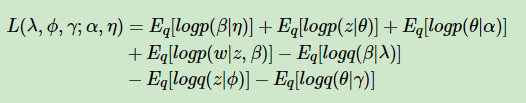
为了简化篇幅,这里只对第一项的展开做详细介绍。在介绍第一项的展开前,我们需要了解指数分布族的性质。指数分布族是指下面这样的概率分布:
![]()
其中,A(x)为归一化因子,主要是保证概率分布累积求和后为1,引入指数分布族主要是它有下面这样的性质:
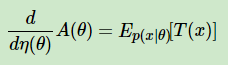
我们的常见分布比如Gamma分布,Beta分布,Dirichlet分布都是指数分布族。有了这个性质,意味着我们在ELBO里面一大推的期望表达式可以转化为求导来完成,这个技巧大大简化了计算量。
ELBO第一项的展开如下:

第三项的期望部分,可以用上面讲到的指数分布族的性质,转化为一个求导过程。即:
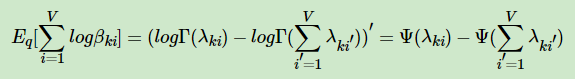
其中: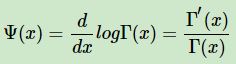
最终,我们得到EBLO第一项的展开式为:
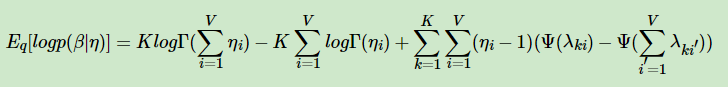
类似的方法求解其他6项,可以得到ELBO的最终关于变分参数λ,ϕ,γ的表达式。其他6项的表达式为:

有了ELBO的具体的关于变分参数λ,ϕ,γ的表达式,我们就可以用EM算法来迭代更新变分参数和模型参数了。
EM算法之E步:获取最优变分参数
有了前面变分推断得到的ELBO函数为基础,我们就可以进行EM算法了。但是和EM算法不同的是这里的E步需要在包含期望的EBLO计算最佳的变分参数。通过ELBO函数对各个变分参数λ,ϕ,γ分别求导并令偏导数为0,可以得到迭代表达式,多次迭代收敛后即为最佳变分参数。
各个变分参数的表达式如下:
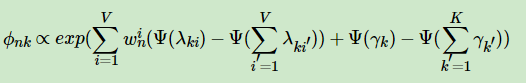
其中,=1当且仅当文档中第n个词为词汇表中第i个词。

由于变分参数λ决定了β的分布,对于整个语料是共有的,因此我们有:
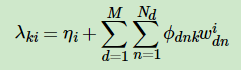
最终我们的E步就是用上面三个式子来更新三个变分参数。当我们得到三个变分参数后,不断循环迭代更新,直到这三个变分参数收敛。当变分参数收敛后,下一步就是M步,固定变分参数,更新模型参数α,η了。
EM算法之M步:更新模型参数
由于我们在E步,已经得到了当前最佳变分参数,现在我们在M步就来固定变分参数,极大化ELBO得到最优的模型参数α,η。使用牛顿法,即通过求出ELBO对于α,η的一阶导数和二阶导数的表达式,然后迭代求解α,η在M步的最优解。
对于α,它的一阶导数和二阶导数的表达式为:
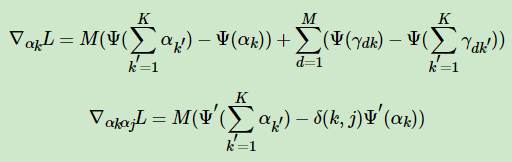
其中,当且仅当k=j时,δ(k,j)=1,否则δ(k,j)=0
对于η,它的一阶导数和二阶导数的表达式为:
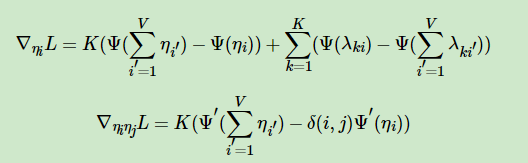
其中,当且仅当i=j时,δ(i,j)=1,否则δ(i,j)=0
最终牛顿法法迭代公式为:
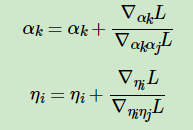
算法结束后,我们可以得到模型的后验参数α,η,以及我们需要的近似模型主题词分布λ,以及近似训练文档主题分布γ。





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








