贝叶斯推断（Bayesian Inference）

豆芽819

已于 2025-03-18 12:50:46 修改

阅读量1.2k

点赞数 39

文章标签：机器学习概率论算法

于 2025-03-16 23:18:26 首次发布

本文链接：https://blog.csdn.net/weixin_71288092/article/details/146302447

版权

1. 贝叶斯定理

贝叶斯定理是贝叶斯推断的数学基础，公式为：

符号解释：
- 𝑃(𝜃∣𝐷)：后验概率（参数𝜃在数据𝐷下的分布）。
- 𝑃(𝐷∣𝜃)：似然函数（数据𝐷在参数𝜃下的概率）。
- 𝑃(𝜃)：先验概率（参数的初始知识）。
- 𝑃(𝐷)：边缘似然（数据的整体概率，常为归一化常数）。

2. 核心步骤

(1) 定义先验分布（Prior）

作用：基于领域知识或历史数据，对参数𝜃的初始不确定性建模。
常见先验：
- 无信息先验：如均匀分布（对参数无偏向）。
- 共轭先验：与似然函数形式匹配，便于计算（如Beta分布与二项似然）。
- 层次先验：超参数本身服从某个分布，适用于复杂模型。

(2) 构建似然函数（Likelihood）

作用：描述观测数据𝐷在给定参数𝜃θ下的生成过程。
示例：
- 高斯分布：𝐷∼𝑁(𝜇,𝜎2)，则似然为 𝑃(𝐷∣𝜇,𝜎2)∝

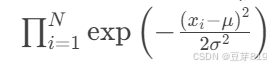
(3) 计算后验分布（Posterior）

目标：结合先验与似然，得到参数𝜃θ的更新后分布。
挑战：高维积分𝑃(𝐷)=∫𝑃(𝐷∣𝜃)𝑃(𝜃)𝑑𝜃通常难以解析求解。
解决方法：
- 解析法：仅适用于共轭先验-似然对（如Beta-Binomial、Gaussian-Gaussian）。
- 近似推断：马尔可夫链蒙特卡洛（MCMC）、变分推断（VI）、拉普拉斯近似。

3. 常用推断方法

(1) 马尔可夫链蒙特卡洛（MCMC）

原理：通过构建马尔可夫链，使其平稳分布为目标后验分布，采样近似积分。
算法：
- Metropolis-Hastings：提议分布生成候选样本，根据接受概率决定是否采纳。
- Gibbs采样：逐维度条件采样，适用于可分参数。
- Hamiltonian Monte Carlo (HMC)：利用哈密顿动力学加速高维空间采样。
优点：精确逼近复杂后验分布。
缺点：计算成本高，收敛诊断复杂。

(2) 变分推断（Variational Inference, VI）

原理：将后验推断转化为优化问题，用简单分布族𝑞(𝜃)q(θ)近似真实后验𝑃(𝜃∣𝐷)P(θ∣D)。
优化目标：最小化KL散度 KL(𝑞(𝜃)∥𝑃(𝜃∣𝐷))。
常用技术：
- 平均场变分推断：假设参数独立分解 𝑞(𝜃)=∏𝑖𝑞𝑖(𝜃𝑖)。
- 随机变分推断（SVI）：结合随机梯度下降，适用于大规模数据。
优点：速度快，适合在线学习。
缺点：近似误差可能较大。

(3) 拉普拉斯近似（Laplace Approximation）

原理：在后验众数（MAP估计）处进行二阶泰勒展开，用高斯分布近似后验。
公式：

适用场景：后验分布接近高斯分布时效果较好。

4. 贝叶斯推断的优势

不确定性量化：直接输出参数的概率分布，而非点估计。
先验知识融合：允许专家经验与数据协同作用。
在线学习能力：后验分布可作为新数据的先验，实现序贯更新。
模型比较：通过边缘似然𝑃(𝐷)比较不同模型的拟合能力（如贝叶斯因子）。

5. 应用场景

(1) 参数估计与模型校准

示例：在设备退化模型中，估计裂纹扩展速率参数的后验分布。
方法：定义物理模型（如Paris公式）的似然函数，结合先验进行MCMC采样。

(2) 预测与不确定性传播

示例：基于后验分布生成剩余寿命（RUL）的预测区间。
步骤：
1. 从后验分布中采样参数𝜃(𝑠)。
2. 对每个𝜃(𝑠)，计算RUL的预测值𝑦(𝑠)。
3. 统计所有𝑦(𝑠)的分位数，得到置信区间。

(3) 假设检验

贝叶斯假设检验：计算不同假设的后验概率比（贝叶斯因子）。
示例：比较设备故障是否由温度（𝐻1）或振动（𝐻2）主导：

6. 工具与库

概率编程语言：
- PyMC3：基于Theano的MCMC和VI库，支持NUTS、ADVI。
- Stan：高性能贝叶斯推断引擎，提供R/Python接口。
- TensorFlow Probability：集成变分推断和MCMC，适合深度学习结合。
可视化工具：
- ArviZ：专用于贝叶斯模型诊断与可视化。
- corner.py：绘制后验分布的角图（corner plot）。

9. 代码示例（pymc）

import pymc as pm 
import numpy as np

# 生成模拟数据
np.random.seed(42)
true_mu = 5.0
data = np.random.normal(true_mu, 1.0, 100)

# 定义贝叶斯模型
with pm.Model() as model:
    # 先验：均值的正态分布（均值=0，标准差=10）
    mu = pm.Normal("mu", mu=0, sigma=10)
    # 似然：数据服从正态分布
    likelihood = pm.Normal("likelihood", mu=mu, sigma=1.0, observed=data)
    # MCMC采样
    trace = pm.sample(2000, tune=1000, chains=4, return_inferencedata=True)  # 添加 return_inferencedata=True

# 后验分析
import arviz as az  # 导入 arviz 库
az.plot_posterior(trace, var_names=["mu"], credible_interval=0.95)  # 使用 arviz 进行后验分析