一元线性回归解决航班正点率和顾客投诉次数之间的关系

 一元线性回归是探索两个变量之间关系的一种统计分析方法，为了探索航班正点率与顾客投诉次数之间的关系我们调查了10家航空公司的航班正点率与顾客投诉次数之间的关系。

 

 

 

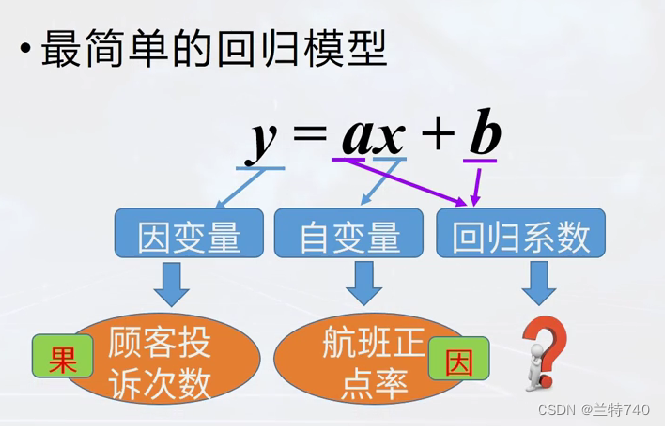
 由最小二乘法通过残差最小化原则我们也可以得到航班正点率与顾客投诉次数之间的关系，但是计算还是比较繁琐的，所以我们来熟悉一下用 Python 进行数据分析的基本流程，首先第一步是调用所必需的包；

#Step1 调用包
from sklearn.linear_model import LinearRegression
import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt

第二步是导入数据，熟悉数据的基本结构；

#Step2 导入数据
data = pd.read_excel('data_airline.xls')
x_data=data.iloc[:,1]
y_data=data.iloc[:,2]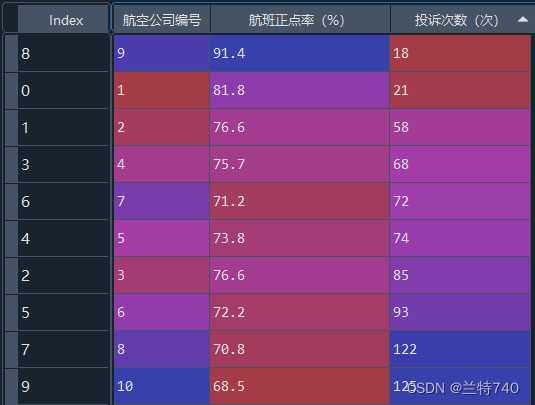

 

第三步是画数据的散点图，看数据的大致结构是什么样的；

#Step3 绘制散点图

#预处理： 设置汉字为黑体
matplotlib.rcParams['font.family'] = 'SimHei' 

#绘制散点图
plt.scatter(x_data,y_data) 
plt.xlabel('航班正点率(%)')
plt.ylabel('投诉次数(次)')
plt.title('航空公司航班正点率与投诉次数关系散点图')
plt.show()

 

第四步确立好模型之后，计算模型所需的参数；

#Step4 创建并拟合模型

#预处理：转换数据格式为sklearn要求格式
x_data=x_data[:,np.newaxis]
y_data=y_data[:,np.newaxis]

#调用最小二乘法函数求回归系数
model=LinearRegression()
model.fit(x_data,y_data)

第五步是评估模型的准确性，判断模型的可适用性；

#Step5 报告结果
# 显示斜率
a = model.coef_[0]
print("自变量x的系数a为: ", np.round(a,2))
#np.round保留小数点设置
# 显示截距
b = model.intercept_
print("常数项（截距）为: ", np.round(b,2))
# 画拟合效果图
plt.plot(x_data,y_data,'b.')
plt.plot(x_data,model.predict(x_data),'r')
plt.show()

 

 

第六步就是用来预测和计算需要的数据。

#Step6 应用--预测
x_test = np.array([[77]])
predict = model.predict(x_test)
print("预测值: ", np.round(predict,2))