主成分分析 (PCA) 简介

主成分分析 (PCA) 简介

1.简要介绍 PCA 的概念

主成分分析 (PCA) 是一种常用的数据降维技术，主要用于从高维数据集中提取出最具信息量的低维子空间。PCA 通过线性变换将原始数据映射到新的坐标系中，使得新坐标系中的变量（主成分）是相互正交的，并且尽可能多地保留原始数据的方差。PCA 有助于简化数据结构，降低数据维度，便于可视化和进一步的分析处理。

PCA 的历史背景

PCA 最早由卡尔·皮尔逊 (Karl Pearson) 于1901年提出，用于统计分析中的降维问题。后来，哈罗德·霍特林 (Harold Hotelling) 在1933年进一步发展了这一方法，使其在现代数据分析和机器学习领域得到了广泛应用。PCA 是一种无监督学习方法，不需要预先设定类别标签，仅根据数据的统计特性进行分析。

PCA 在数据科学中的地位

PCA 在数据科学中具有重要地位，广泛应用于各个领域，如图像处理、基因表达分析、金融数据分析、市场营销和社会科学研究等。通过减少数据维度，PCA 能够提高算法的效率和性能，减少计算资源的消耗，并在一定程度上缓解“维度灾难”问题。此外，PCA 还常用于数据预处理阶段，为后续的机器学习和统计分析提供简洁、有效的输入数据。

2.PCA 的工作原理

数据标准化的重要性

在进行 PCA 之前，数据标准化是非常重要的一步。标准化的目的是消除不同特征之间的量纲差异，使每个特征在相同的尺度上进行比较。通常采用 Z-score 标准化方法，即将每个特征的均值设为0，标准差设为1。标准化公式为： $x\prime =\frac{x-\mu }{\sigma }$ 其中，$x$是原始数据，$\mu$ 是均值，$\sigma$ 是标准差。

协方差矩阵的计算

标准化后的数据可以用来计算协方差矩阵。协方差矩阵反映了数据中每对特征之间的线性关系，矩阵中的元素表示不同特征之间的协方差。设标准化后的数据矩阵为 $X$，则协方差矩阵 $\Sigma$ 计算公式为： $\Sigma =\frac{1}{n-1}{X}^{T}X$ 其中，$n$ 是样本数量，$X^T$ 是 $X$ 的转置。

特征值和特征向量的计算

协方差矩阵计算完成后，需要求解该矩阵的特征值和特征向量。特征值表示数据在对应特征向量方向上的方差大小。通过求解特征值和特征向量，确定主成分方向。特征值越大，表示该方向上数据的变异性越大，对应的特征向量即为主成分。求解特征值和特征向量的公式为： $\Sigma v=\lambda v$ 其中，$\lambda$ 是特征值，$v$ 是特征向量。

选择主要成分

根据特征值的大小排序，选择前 kkk 个最大的特征值对应的特征向量作为主要成分。通常通过累计方差贡献率来确定 kkk 的值，确保所选择的主成分能解释足够多的数据方差。累计方差贡献率计算公式为： 累计方差贡献率=$\sum i=\frac{{\sum }_{i=1}^k{\lambda }_i}{{\sum }_{i=1}^p{\lambda }_i}$ 其中，$\lambda i$ 为特征值，$p$ 为特征总数。

新特征空间的构建

选定主要成分后，将原始数据投影到这些主成分构成的新特征空间中。新特征空间中的每个轴对应一个主成分，投影后的数据保留了原始数据中大部分的变异性，同时降低了维度。投影公式为： $Z=XW$ 其中，$Z$ 是投影后的数据，$X$ 是标准化后的原始数据，$W$ 是主要成分矩阵（由选定的特征向量构成）。

3.PCA 的优缺点

优点

• 降低数据的复杂性
  • 通过提取主要成分，将高维数据映射到低维空间，简化数据结构，便于分析和处理。
• 提高模型的训练速度
  • 降维后数据维度减少，减少计算量，从而提高机器学习模型的训练速度和预测效率。
• 减少噪声的影响
  • PCA 能够去除数据中的噪声成分，使得数据更为纯净，有助于提高模型的性能和稳定性。

缺点

• 可能丢失有用信息
  • 在降维过程中，一些包含重要信息的特征可能会被忽略，导致信息损失。
• 难以解释的主成分
  • 主成分是线性组合，难以直接解释其物理或实际意义，增加了解释结果的难度。
• 对数据的线性假设
  • PCA 假设数据之间的关系是线性的，对于非线性数据表现较差，限制了其应用范围。

4.PCA 的实现步骤

1. 数据标准化

   • 对数据进行标准化处理，使每个特征的均值为0，标准差为1，消除不同特征之间的量纲差异。
   • 标准化公式为：
     $$x^{\prime }=\frac{x-\mu }{\sigma }$$
     其中，( x ) 是原始数据，( \mu ) 是均值，( \sigma ) 是标准差。

2. 计算协方差矩阵

   • 计算标准化后的数据矩阵的协方差矩阵，反映数据中每对特征之间的线性关系。
   • 协方差矩阵公式为：
     $$\Sigma =\frac{1}{n-1}{X}^{T}X$$
     其中，( n ) 是样本数量，( X^T ) 是 ( X ) 的转置。

3. 计算特征值和特征向量

   • 求解协方差矩阵的特征值和特征向量，确定主成分方向。
   • 特征值和特征向量的公式为：
     $$\Sigma v=\lambda v$$
     其中，( \lambda ) 是特征值，( v ) 是特征向量。

4. 选择主要成分

   • 根据特征值的大小排序，选择前 ( k ) 个最大的特征值对应的特征向量作为主要成分。
   • 累计方差贡献率计算公式为：
     $$\text{累计方差贡献率}=\frac{{\sum }_{i=1}^k{\lambda }_i}{{\sum }_{i=1}^p{\lambda }_i}$$
     其中，( \lambda_i ) 为特征值，( p ) 为特征总数。

5. 构建新特征空间

   • 将原始数据投影到选定的主要成分构成的新特征空间中。
   • 投影公式为：
     $$Z=XW$$
     其中，( Z ) 是投影后的数据，( X ) 是标准化后的原始数据，( W ) 是主要成分矩阵（由选定的特征向量构成）。

6. 将数据映射到新空间

   • 最终的映射结果即为降维后的数据，可以用于进一步的分析和处理。

5.PCA代码实现

import numpy as np
import matplotlib.pyplot as plt

# 生成示例数据
np.random.seed(0)
data = np.random.rand(50, 3)  # 50个样本，3个特征

# 数据标准化
def standardize(data):
    mean = np.mean(data, axis=0)
    std = np.std(data, axis=0)
    standardized_data = (data - mean) / std
    return standardized_data

data_standardized = standardize(data)

# 计算协方差矩阵
def compute_covariance_matrix(data):
    n_samples = data.shape[0]
    covariance_matrix = np.dot(data.T, data) / (n_samples - 1)
    return covariance_matrix

cov_matrix = compute_covariance_matrix(data_standardized)

# 计算协方差矩阵的特征值和特征向量
def eigen_decomposition(cov_matrix):
    eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
    return eigenvalues, eigenvectors

eigenvalues, eigenvectors = eigen_decomposition(cov_matrix)

# 根据特征值的大小排序，选择前k个主要成分
def select_principal_components(eigenvalues, eigenvectors, k):
    sorted_indices = np.argsort(eigenvalues)[::-1]  # 从大到小排序
    sorted_eigenvalues = eigenvalues[sorted_indices]
    sorted_eigenvectors = eigenvectors[:, sorted_indices]
    selected_eigenvectors = sorted_eigenvectors[:, :k]
    return selected_eigenvectors

k = 2  # 选择前2个主成分
principal_components = select_principal_components(eigenvalues, eigenvectors, k)

# 将数据映射到新特征空间中
def transform_data(data, principal_components):
    transformed_data = np.dot(data, principal_components)
    return transformed_data

data_transformed = transform_data(data_standardized, principal_components)
print("Transformed Data:\n", data_transformed)

# 可视化结果
def plot_pca(data, transformed_data):
    plt.figure(figsize=(14, 6))

    # 原始数据的散点图（前两个特征）
    plt.subplot(1, 2, 1)
    plt.scatter(data[:, 0], data[:, 1], alpha=0.7)
    plt.title("Original Data (First Two Features)")
    plt.xlabel("Feature 1")
    plt.ylabel("Feature 2")

    # PCA转换后的散点图（两个主成分）
    plt.subplot(1, 2, 2)	
    plt.scatter(transformed_data[:, 0], transformed_data[:, 1], alpha=0.7, color='r')
    plt.title("PCA Transformed Data (First Two Principal Components)")
    plt.xlabel("Principal Component 1")
    plt.ylabel("Principal Component 2")

    plt.tight_layout()
    plt.show()

plot_pca(data, data_transformed)

结果

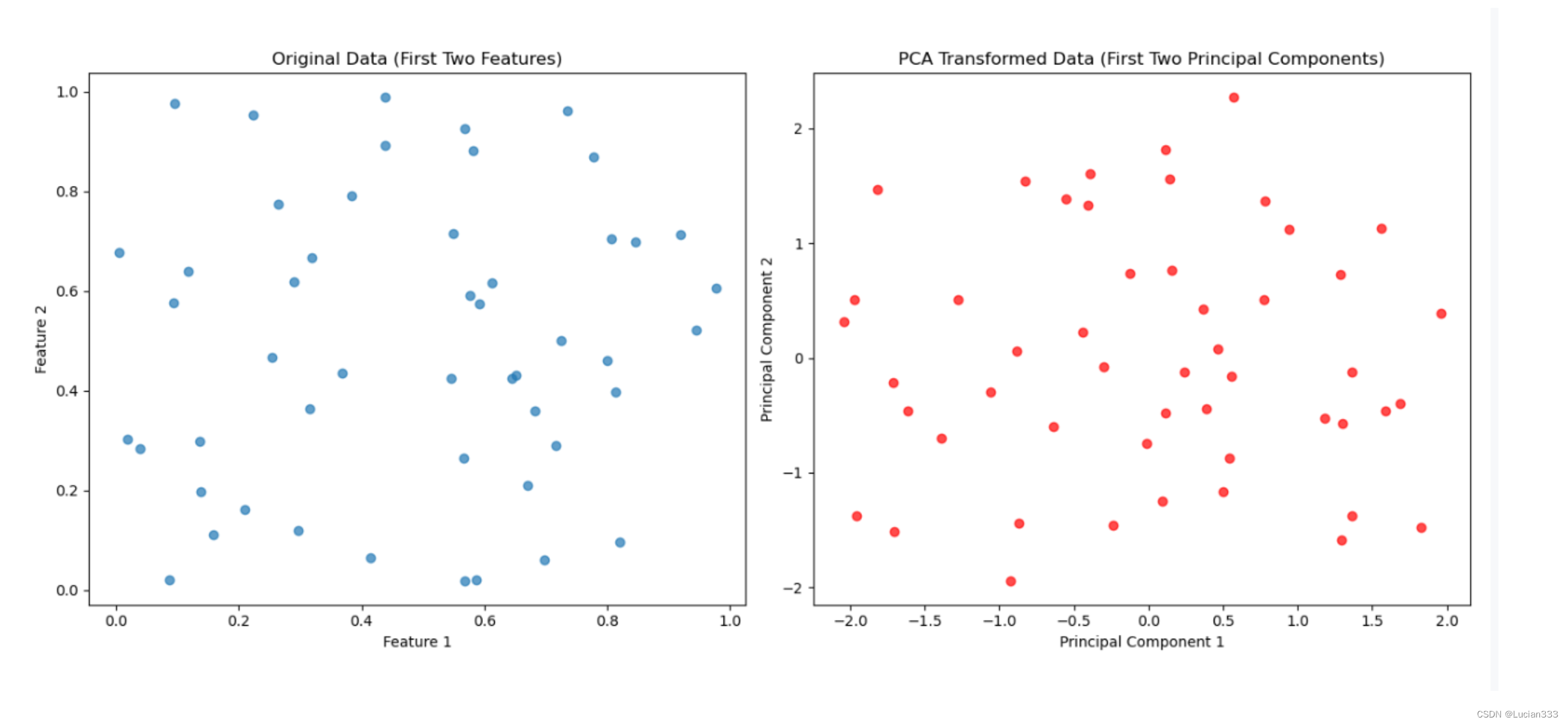
在这里插入图片描述

6.总结

• 回顾 PCA 的主要概念

  • 主成分分析 (PCA) 是一种用于降维的无监督学习方法，通过线性变换将原始高维数据投影到低维空间，同时尽可能多地保留数据的方差。
  • PCA 的核心步骤包括数据标准化、计算协方差矩阵、求解特征值和特征向量、选择主要成分以及构建新特征空间。

• 强调 PCA 的应用价值

  • PCA 在数据科学和机器学习中有广泛应用，如数据降维、噪声过滤、数据可视化、模式识别和图像压缩等。
  • 通过降低数据的复杂性，PCA 可以提高模型的训练速度和预测效率，减少计算资源的消耗，并缓解“维度灾难”问题。
  • PCA 能够去除数据中的噪声成分，使得数据更为纯净，有助于提高模型的性能和稳定性。

• 提示进一步学习的方向

  • 学习其他降维方法，如线性判别分析 (LDA)、独立成分分析 (ICA) 和 t-SNE 等，以应对不同类型的数据和应用场景。
  • 探索非线性降维方法，如核 PCA 和自编码器，以解决 PCA 对数据的线性假设限制。
  • 实践更多的 PCA 应用案例，深入理解其在实际问题中的应用效果和优化技巧。

7.参考文献

• 相关书籍、论文和在线资源链接
  • Pearson, K. (1901). On lines and planes of closest fit to systems of points in space. Philosophical Magazine, 2(11), 559-572.
  • Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. Journal of Educational Psychology, 24(6), 417-441.
  • Jolliffe, I. T. (2002). Principal Component Analysis. Springer Series in Statistics.
  • 在线教程和文档：如 Scikit-learn 官方文档、Coursera 和 Udacity 上的相关课程等。

ts. Journal of Educational Psychology, 24(6), 417-441.

• Jolliffe, I. T. (2002). Principal Component Analysis. Springer Series in Statistics.
• 在线教程和文档：如 Scikit-learn 官方文档、Coursera 和 Udacity 上的相关课程等。