算法导论学习之线性时间排序

          在没有限定条件的情况下，目前的排序算法的最好的时间复杂度大都在O(n lgn)左右，而当加入了一些限定条件后，一些排序算法可以达到线性的时间复杂度。下面让我们来看两个线性时间复杂度的排序算法。

一计数排序

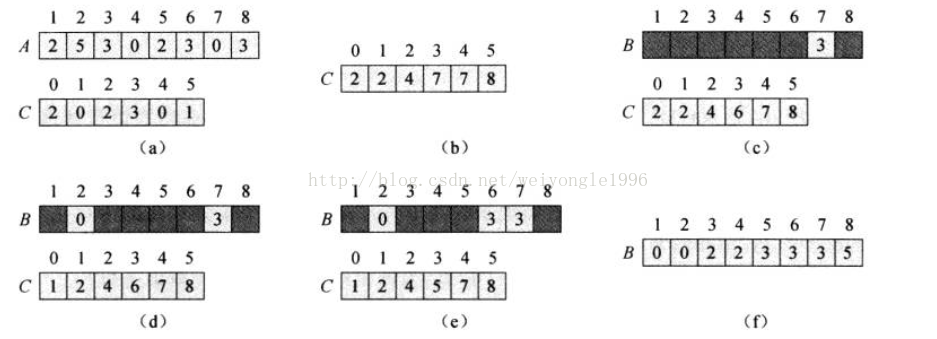
       计数排序要求要排序的数要在一定区间内（0，k），当k=O(n)时，排序的时间复杂度为线性的。  计数排序需要两个辅助数组B[0...n]存放排序的输出和C[0...k]提供临时存储空间，其值表示数组元素在排好序的数组中的位置。计数排序的基本思想是对每一个数组元素x，确定小于x值的元素个数，这样就可以知道x的位置。具体实现为先将数组C初始化为零，然后遍历A数组，根据A数组中的值，去C数组中找到对应的下标，将其值加一。如若A[0]=3,则找到C[3],然后C[3]++。然后遍历C数组，将C数组当前元素的值置为当前元素值加上前一个元素的值，这样C数组中的元素值就能够标示待排序数组在排好序数组中的位置（都会在C数组标示的位置或标示的位置之前），因为C数组中的元素此时代表的便是小于等于x元素的个数。然后将A数组中的元素按照C数组中的标示放到B数组中，B数组即为有序数组。伪代码如下：

一次排序的实现过程示意图如下：

以上即为计数排序的思想和伪代码，下面我们再来看另一种排序--基数排序

二基数排序

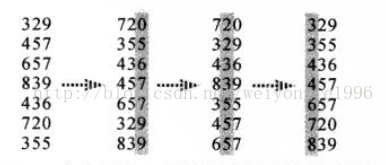
        计数排序当k的值很大时，会耗费很多时间（初始化C数组就会耗费很多时间和空间）。所以在计数排序的基础上又有基数排序，基数排序的主要思想为按位排序，即从最低位开始每一位单独排序，当排完最高位时数组有序。下面是一趟基数排序的示意图：

对每一位的排序运用计数排序是非常快的，因为只有十个数字,k=10。所以基数排序能够处理的数字范围大一些。以上即为计数排序和基数排序的一些内容。