凸优化问题简述

 简单来说，凸（Convex）优化是满足一定条件的最优化问题，凸优化问题更容易解决，非凸（ Non-Convex）优化问题更难解决。

在数学上，凸和非凸可以用来形容集合、函数、优化问题，对于集合，只要集合中任意两点连线上所在点仍然处于集合内，他就是凸集合。对于函数来说，最简单的XY坐标系上的一条曲线，凸和凹就很直观。

严格来说，凸优化问题(convex optimization)的定义是目标函数是凸的，且可行域是凸的。不符合这个定义的优化问题就是非凸的优化问题(non-convex optimization)

对于优化问题，举几个常见的nonconvex例子,通常2次以上的polynomial不论出现在目标函数或约束条件里,都是noconvex,更不用说什么sin、cos函数了
 

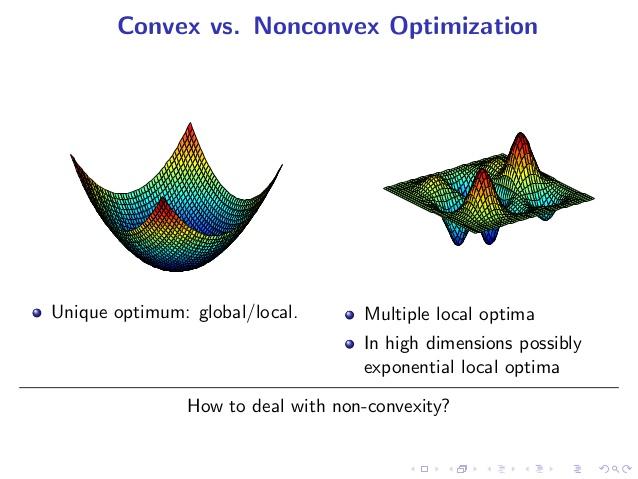
为什么凸优化问题更容易解决呢？因为凸优化问题中局部最优解同时也是全局最优解，这个特性使凸优化问题在一定意义上更易于解决，而一般的非凸最优化问题相比之下更难解决。

由于这个性质,只要设计一个较为简单的局部算法,例如贪婪算法(GreedyAlgorithm)或梯度下降法 (GradientDecent),收敛求得的局部最优解即为全局最优。因此求解凸优化问题相对来说是比较高效的。

而非凸优化问题被认为是非常难求解的,因为可行域集合可能存在无数个局部最优点,通常求解
全局最优的算法复杂度是指数级的(NP难)。如下图:

最经典的算法要算蒙特卡罗投点法,大概思想便是随便投个点,然后在附近区域(可以假设convex)用凸优化方法进行搜索,得到局部最优值。然后随机再没个点,再找到局部最优点。如此反复,直到满足终止条件。