人工智能/机器学习基础知识——隐马尔科夫模型（Hidden Markov Model，HMM）

隐马尔科夫模型

Hidden Markov Model（HMM）

• 两组变量

  • 状态变量：表示第$i$时刻的系统状态

    隐藏的，不可观测的（亦被称为隐变量）

    { y 1 , y 2 , . . . , y n } ， y i ∈ γ \{y_1, y_2, ..., y_n\}，y_i \in γ {y1​,y2​,...,yn​}，yi​∈γ

    • 取值范围：N个可能取值的离散空间

      { s 1 , s 2 , . . . , s N } \{s_1, s_2, ..., s_N\} {s1​,s2​,...,sN​}

  • 观测变量：表示第$i$个时刻的观测值

    { x 1 , x 2 , . . . , x n } \{x_1, x_2, ..., x_n\} {x1​,x2​,...,xn​}

    • 取值范围：连续或离散

      { o 1 , o 2 , . . . , o M } \{o_1, o_2, ..., o_M\} {o1​,o2​,...,oM​}

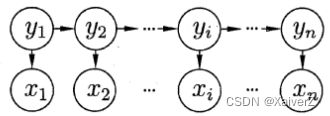
• 图中箭头表示变量间的依赖关系

  马尔可夫链（Markov Chain）：系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态

  • 在任一时刻，观测变量的取值仅依赖于状态变量，即$x_t$由$y_t$确定，与其他状态变量及观测变量的取值无关

  • $t$时刻的状态$y_t$仅依赖于$t-1$时刻的状态$y_{t-1}$，与此前$t-2$个状态无关

  

  • 基于这种依赖关系，所有变量的联合概率分布为：

    $$P\left(x_1,y_1,\dots ,x_n,y_n\right)=P\left(y_1\right)P\left(x_1\mid y_1\right)\prod _{i=2}^{n}P\left(y_i\mid y_{i-1}\right)P\left(x_i\mid y_i\right)$$

• 除了结构信息，欲确定一个隐马尔科夫模型还需以下三组参数

  • 状态转移概率：模型在各个状态间转换的概率，通常记为矩阵$A=[a_{ij}{]}_{N\times N}$

    $$a_{ij}=P\left(y_{t+1}=s_j\mid y_t=s_i\right),i⩽i,j⩽N$$
    表示在任意时刻$t$，若状态为$s_i$，则在下一时刻状态为$s_j$的概率

  • 输出观测概率：模型根据当前状态获得各个观测值的概率，通常记为矩阵$B=[b_{ij}{]}_{N\times M}$

    $$b_{ij}=P\left(x_t=o_j\mid y_t=s_i\right),1⩽i⩽N,1⩽j⩽N$$
    表示在任意时刻$t$，若状态为$s_i$，则观测值$o_j$被获取的概率

  • 初始状态概率：模型在初始时刻各状态出现的概率，通常记为$\pi =({\pi }_1,{\pi }_2,...,{\pi }_N)$

    $${\pi }_i=P\left(y_1=s_i\right),1⩽i⩽N$$
    表示模型的初始状态为$s_i$的概率

• 通过指定状态空间$\gamma$、观测空间$\chi$和上述三组参数，就能确定一个HMM，通常用其参数$\lambda =[A,B,\pi ]$来指代。给定HMM，它按如下过程产生观测序列 { x 1 , x 2 , . . . , x n } \{x_1, x_2, ..., x_n\} {x1​,x2​,...,xn​}

  1. 设置$t=1$，并根据初始状态概率$\pi$选择初始状态$y_1$
  2. 根据状态$y_t$和输出观测概率$B$选择观测变量取值$x_t$
  3. 根据状态$y_t$和状态转移矩阵$A$转移模型状态，即确定$y_{t+1}$
  4. 若$t<n$，设置$t=t+1$，并转到第2步，否则停止

• HMM的三个基本问题

  • 给定模型$\lambda =[A,B,\pi ]$，如何有效计算其产生观测序列 x = { x 1 , x 2 , . . . , x n } x = \{x_1, x_2, ..., x_n\} x={x1​,x2​,...,xn​}的概率$P(x|\lambda )$？换言之，如何评估模型与观测序列之间的匹配程度？

  • 给定模型$\lambda =[A,B,\pi ]$和观测序列 x = { x 1 , x 2 , . . . , x n } x = \{x_1, x_2, ..., x_n\} x={x1​,x2​,...,xn​}，如何找到与此观测序列最匹配的状态序列 y = { y 1 , y 2 , . . . , y n } y = \{y_1, y_2, ..., y_n\} y={y1​,y2​,...,yn​}？换言之，如何根据观测序列推断出隐藏的模型状态？

  • 给定观测序列 x = { x 1 , x 2 , . . . , x n } x = \{x_1, x_2, ..., x_n\} x={x1​,x2​,...,xn​}，如何调整模型参数$\lambda =[A,B,\pi ]$使得该序列出现的概率$P(x|\lambda )$最大？换言之，如何训练模型使其能最好地描述观测数据？