向量的二范数平方求导

最新推荐文章于 2024-08-13 14:37:05 发布
最新推荐文章于 2024-08-13 14:37:05 发布
阅读量1w 收藏 52
点赞数 15
分类专栏： 数学
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/wistonty11/article/details/123387609
版权

范数 数学符号 简写规则 矩阵运算 线性代数
关键词由CSDN通过智能技术生成 
2022.3.9

∣ ∣ x ∣ ∣ 2 ||x||^2 ∣∣x∣∣2：
规则1：范式是写再下面的，如果是2常常省略。所以 ∣ ∣ x ∣ ∣ 2 = ∣ ∣ x ∣ ∣ 2 2 ||x||^2=||x||^2_2 ∣∣x∣∣2=∣∣x∣∣22​;
规则2：
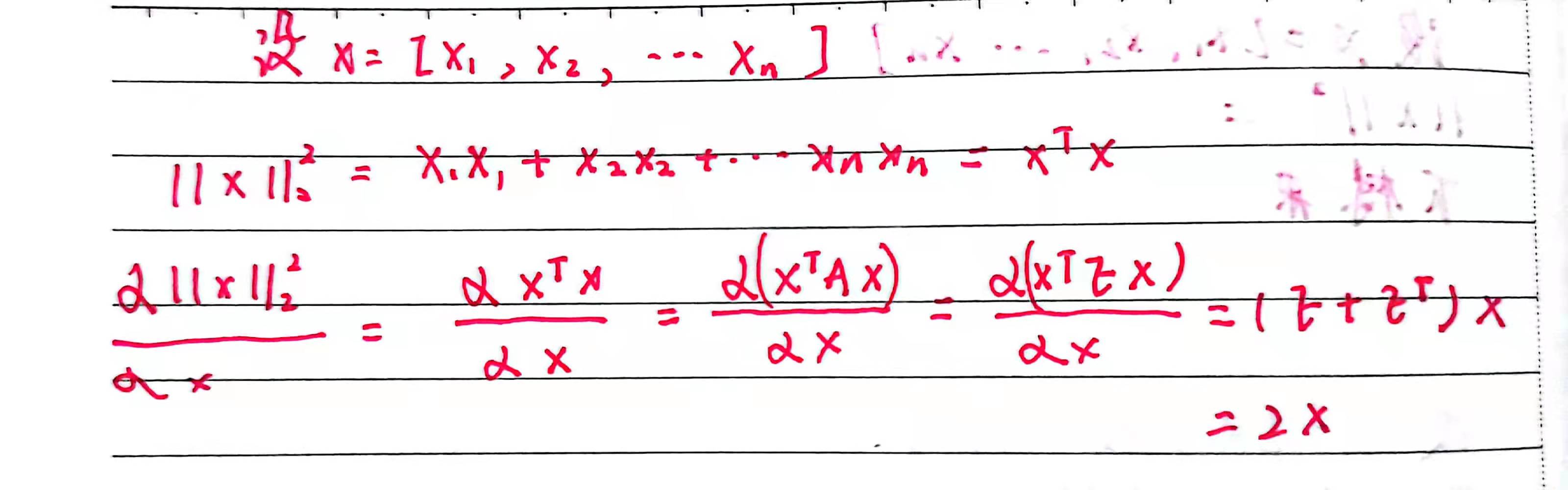
>在这里插入图片描述
【尝试推导】在这里插入图片描述

范数与导数
林景的博客
09-11 3690
范数与导数的基本概念
矩阵范数及其求导
weixin_30598225的博客
09-19 938
在机器学习的特征选择中，利用选择矩阵的范数对选择矩阵进行约束，即是正则化技术，是一种稀疏学习。 矩阵的L0,L1范数 为了度量稀疏矩阵的稀疏性，则定义矩阵的一种范数，为：∥W∥1=∑i,j|Wi,j|。即为矩阵所有元素的绝对值之和，能够描述接矩阵的稀疏性，但是在优化时，难度较大，是将情况向矩阵中元素尽可能是0的方向优化。 1）L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化...
证明矩阵A二范数的平方等于A^T*A的二范数
weixin_43558910的博客
03-07 5469
证明矩阵二范数的平方等于转置矩阵与原矩阵相乘后的二范数
数学：二范数的平方求导
ShellDawn的博客
03-04 2万+
L = ||W||^2 D(L) / D(W) = 2 * W * D(W) / D(W) = 2 * W 所以： L = 1/2 * ||W||^2 D(L) / D(W) = W
范数平方的展开公式
chen的博客
05-13 4052
对于一个向量x∈Rnx∈Rn∥x∥2x⋅x∑i1nxi2∥x∥2x⋅xi1∑n​xi2​这里，xix_ixi​表示向量x\mathbf{x}x的第iii个分量。
l2范数求导_Deep learning：二十七(Sparse coding中关于矩阵的范数求导)
weixin_29149931的博客
12-23 1531
前言：由于在sparse coding模型中求系统代价函数偏导数时需要用到矩阵的范数求导，这在其它模型中应该也很常见，比如说对一个矩阵内的元素值进行惩罚，使其值不能过大，则可以使用F范数(下面将介绍)约束，查阅了下矩阵范数求导的相关资料，本节就简单介绍下。首先，网络上有大把的人把2范数和F=2时的范数混为一谈，或者说把矩阵p范数和诱导p范数混淆了(也有可能是因为各个版本书所定义的不同吧)。下面我还...
向量二范数求导
DeniuHe的博客
08-27 6424
整个国内网站上竟然搜不到向量二范式求导公式。 发帖的国内 学者全部都搞混了，把二范数平方求导当做了二范数求导。竟然还被无数转载，悲伤~
向量的2范数求导？
热门推荐
Charles5101的博客
01-06 4万+
  ，  A: ， 即 A(x)=b，   b ，  是求A(x)-b的2范数。 问题：对    求一阶导   .    解答过程如下：   原式等于     对x求导得：     这里主要用到的是向量和矩阵的求导公式。分别为        和      此外还有向量2范数的定义式。   Reference： [1] https://www.zhihu.com/ques...
向量二范数的求导问题
Mr_Lowbee的博客
02-18 1万+
现有目标函数： f(x)=12∥Ax−b∥22 f(x)=\frac{1}{2} \parallel Ax-b \parallel_2^2 f(x)=21​∥Ax−b∥22​ 其中A∈RN×mA\in \mathbb{R}^{N \times m}A∈RN×m,x∈Rmx \in \mathbb{R}^mx∈Rm,b∈Rnb\in \mathbb{R}^nb∈Rn 则求f′(x)f^{'}(x)f...
l2范数求导_稀疏编码学习笔记（二）L2范数
weixin_42513546的博客
01-27 1939
L2范数除了L1范数，还有一种更受宠幸的规则化范数是L2范数: ||W||2。它也不逊于L1范数，它有两个美称，在回归里面，有人把有它的回归叫“岭回归”(Ridge Regression)，有人也叫它“权值衰减weight decay”。这用的很多吧，因为它的强大功效是改善机器学习里面一个非常重要的问题：过拟合。至于过拟合是什么，上面也解释了，就是模型训练时候的误差很小，但在测试的时候误差很大，也...
l2范数求导_机器学习中的范数规则化之（一）L0、L1与L2范数
weixin_39997443的博客
12-23 1064
source:https://blog.csdn.net/zouxy09/article/details/24971995zouxy09@qq.comhttp://blog.csdn.net/zouxy09今天我们聊聊机器学习中出现的非常频繁的问题：过拟合与规则化。我们先简单的来理解下常用的L0、L1、L2和核范数规则化。最后聊下规则化项参数的选择问题。这里因为篇幅比较庞大，为了不吓到大家，我将...
[Doc][基础]加权二次范数
martinkeith的博客
08-13 1286
加权二次范数是一种用于衡量向量大小的扩展形式，通过引入权重矩阵QQQ来调整不同分量的重要性。它在优化问题中非常有用，尤其是当我们希望对不同分量施加不同的影响或强调时。
矩阵，向量二范数求导
JGL121314的博客
10-04 3442
向量的2范数求导？_Charles5101的博客-CSDN博客_二范数求导
向量的求导
算法攻城狮
10-03 443
  元素对想两矩阵求导依然简单 行对列与列对行  注意分母的对应 行对行  列对列 矩阵对行向量以及列向量 m*np 对矩阵求导 先将X看成行向量，再将Y看成列向量...
向量及矩阵的求导
ZhuNian的学习乐园
04-19 397
在学习机器学习里岭回归的公式推导时，涉及到向量求导的相关数学公式推导过程，不同的是：岭回归的代价函数是在多项式回归上的代价函数上加了对参数的约束项。 本文基于最小二乘法的推导公式来求解多项式回归系数以及岭回归系数的推导过程。并附加一些向量及矩阵的求导公式。 1 岭回归的公式推导 采用最小二乘法，定义损失函数为残差的平方，最小化损失函数，公式进行直接求解： 岭回归是对最小二乘回归的一种补充，下面是...
向量/矩阵求导
m0_59941705的博客
08-17 184
二范数平方求导：向量求导链式法则：二范数求导：
向量求导的二个公式
小红鱼的博客
04-28 981
∂xTa∂x=∂aTx∂x=a\frac{\partial \mathbf{x}^{T} \mathbf{a}}{\partial \mathbf{x}}=\frac{\partial \mathbf{a}^{T} \mathbf{x}}{\partial \mathbf{x}}=\mathbf{a}∂x∂xTa​=∂x∂aTx​=a ∂xTBx∂x=(B+BT)x\frac{\partial \...
常用的向量求导公式
xwemin的专栏
12-24 1540
​​​​​ ​​
矩阵范数求导
最新发布
03-16
<think>嗯，矩阵范数的求导，这个问题看起来有点挑战性。首先，我需要回忆一下矩阵范数的定义和常见的类型。矩阵范数有很多种，比如Frobenius范数、谱范数、核范数等等。不同的范数可能有不同的求导方式，所以得先确定用户指的是哪一种。不过通常在没有特别说明的情况下，可能默认是Frobenius范数，因为它在优化问题中比较常见，比如在机器学习中的矩阵分解或正则化项中。 接下来，我得想一下如何对矩阵变量进行求导。矩阵求导涉及到将导数表示为与原矩阵同维的矩阵，每个元素对应位置的偏导数。不过这里可能需要用到矩阵微积分中的一些规则，比如标量对矩阵的导数，结果应该是一个矩阵，其每个元素是标量对原矩阵对应元素的偏导。 假设我们考虑Frobenius范数，对于一个矩阵A，其Frobenius范数是所有元素平方和的平方根，即||A||_F = sqrt(sum_{i,j} A_{i,j}^2)。如果我们要对这个范数求导，比如求d||A||_F / dA，可能需要先处理平方后的形式，因为平方后的范数更容易求导。比如，d(||A||_F^2)/dA 就是2A，因为每个元素的平方导数是2A_{i,j}，所以整个导数矩阵就是2A。然后再通过链式法则，考虑平方根的导数，即如果f(A) = sqrt(g(A))，那么f’(A) = (1/(2*sqrt(g(A)))) * g’(A)。所以d||A||_F/dA应该是 (1/(||A||_F)) * A，前提是A不是零矩阵。 不过这里可能需要更严谨的推导。比如，假设我们有函数f(A) = ||A||_F，那么f(A) = sqrt{tr(A^T A)}，因为Frobenius范数等于矩阵A的迹的平方根。因此，导数df/dA就是 (1/(2*sqrt{tr(A^T A)})) * d(tr(A^T A))/dA。而tr(A^T A)对A的导数应该是2A，所以最后结果确实是A / ||A||_F，当||A||_F ≠ 0时。 如果是其他范数，比如谱范数（最大奇异值），那么求导可能更复杂，因为涉及到奇异值分解。这时候可能需要用更高级的矩阵微积分技巧，比如使用链式法则和子梯度，尤其是当矩阵有重复的最大奇异值时，导数可能不唯一，变成子梯度的形式。不过用户可能主要关心Frobenius范数的情况，所以先重点考虑这个。 另外，用户可能想知道在优化问题中如何处理矩阵范数的导数，比如在损失函数中加入正则化项时，如何计算梯度。例如，若目标函数是||X||_F^2，那么梯度就是2X，这在实际应用中很常见，比如岭回归中的权重衰减。 但用户的问题更广泛，是“矩阵范数求导”，所以可能需要更一般性的介绍，涵盖不同的范数类型，并指出它们的求导方法有何不同。同时，可能需要提到矩阵变量的函数的导数定义，以及如何利用矩阵微分来进行计算。 例如，对于L1范数（元素绝对值之和），导数会是符号函数，但由于矩阵的L1范数可能有不同的定义，需要确认是否指元素绝对值之和，还是其他形式。如果是元素绝对值之和，那么导数矩阵中的每个元素是对应位置的符号，但要注意在零点处不可导。 不过矩阵范数的L1通常可能指的是列绝对值和的最大值，或者行绝对值和的最大值，这需要具体情况具体分析。这时候导数可能涉及到对最大值对应的列或行的处理，类似于向量无穷范数的导数，这时候在最大值点处可能导数存在子梯度。 总结来说，矩阵范数的求导需要根据具体的范数类型来选择合适的求导方法，常见的Frobenius范数相对简单，而其他范数可能涉及更复杂的分析，如奇异值分解或子梯度。在回答时需要分情况讨论，并给出具体的例子和步骤，帮助用户理解不同情况下的处理方法。</think>矩阵范数的求导是矩阵微积分中的重要内容，在优化、机器学习等领域有广泛应用。下面从常见矩阵范数类型入手，逐步介绍求导方法： --- ### 一、Frobenius范数的求导 **定义**：对矩阵$A \in \mathbb{R}^{m \times n}$，其Frobenius范数为： $$||A||_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n a_{ij}^2}$$ **求导步骤**： 1. **平方处理**：先对平方形式求导，简化计算： $$||A||_F^2 = \text{tr}(A^T A)$$ 2. **导数计算**： $$\frac{\partial ||A||_F^2}{\partial A} = 2A$$ 3. **链式法则**：对原范数应用链式法则： $$\frac{\partial ||A||_F}{\partial A} = \frac{A}{||A||_F} \quad (\text{当 } ||A||_F \neq 0)$$ --- ### 二、谱范数（2-范数）的求导 **定义**：矩阵的最大奇异值，即： $$||A||_2 = \sigma_{\text{max}}(A)$$ **求导方法**： 1. **奇异值分解**：设$A = U \Sigma V^T$，最大奇异值为$\sigma_1$，对应左右奇异向量$u_1, v_1$。 2. **导数公式**： $$\frac{\partial ||A||_2}{\partial A} = u_1 v_1^T$$ *当$\sigma_1$唯一时成立，否则需考虑子梯度集合。* --- ### 三、核范数（迹范数）的求导 **定义**：所有奇异值之和： $$||A||_* = \sum_{i=1}^r \sigma_i(A) \quad (r为A的秩)$$ **求导步骤**： 1. **奇异值分解**：$A = U \Sigma V^T$。 2. **导数公式**： $$\frac{\partial ||A||_*}{\partial A} = U V^T$$ *假设所有奇异值非零且无重复，否则需调整。* --- ### 四、一般矩阵范数求导方法 1. **矩阵微分**：将标量函数$f(A)$展开为微分形式$df = \text{tr}(B^T dA)$，则$\frac{\partial f}{\partial A} = B$。 2. **链式法则**：复合函数需分解为基本运算（如迹、行列式等）逐步求导。 3. **子梯度处理**：当范数不可导时（如存在多个最大奇异值），需使用子梯度集合。 --- ### 五、应用示例 **问题**：优化问题中最小化$f(X) = ||X||_F^2$，求梯度。 **解**： 1. 目标函数展开： $$f(X) = \text{tr}(X^T X)$$ 2. 计算微分： $$df = \text{tr}(2X^T dX)$$ 3. 提取梯度： $$\frac{\partial f}{\partial X} = 2X$$ --- ### 六、注意事项 1. **维度匹配**：导数结果需与原矩阵维度一致。 2. **特殊点处理**：如$A=0$时Frobenius范数不可导。 3. **数值稳定性**：实际计算中需避免除以零（如对$||A||_F$分母加小常数）。 通过以上步骤，可根据具体范数类型选择合适的求导方法。实际应用中，Frobenius范数因可导性良好且计算简单，常被优先使用。
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

羊老羊

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值