JavaScript 深度学习（一）

原文：zh.annas-archive.org/md5/ea99677736c22d68b5818a18b5a9213a

译者：飞龙

协议：CC BY-NC-SA 4.0

第一部分：动机与基本概念

第一部分 包括一个单独的章节，为您介绍将构成本书其余部分背景的基本概念。这些包括人工智能、机器学习和深度学习以及它们之间的关系。第一章 还探讨了在 JavaScript 中实践深度学习的价值和潜力。

第一章：深度学习和 JavaScript

本章内容

• 深度学习是什么以及它与人工智能（AI）和机器学习的关系

• 使深度学习在各种机器学习技术中脱颖而出的因素，以及导致当前“深度学习革命”的因素

• 使用 TensorFlow.js 进行 JavaScript 中深度学习的原因

• 本书的总体组织

人工智能（AI）周围的热议完全有其原因：即所谓的深度学习革命确实已经发生。 深度学习革命 指的是从 2012 年开始并持续至今的深度神经网络速度和技术上的迅速进步。自那时以来，深度神经网络已被应用到越来越广泛的问题中，在某些情况下使得机器能够解决以前无法解决的问题，并在其他情况下显著提高了解决方案的准确性（有关示例，请参见 表 1.1）。 对于 AI 专家来说，神经网络在许多方面的突破是令人震惊的。对于使用神经网络的工程师来说，这一进步所带来的机遇是令人振奋的。

表 1.1。自 2012 年深度学习革命开始以来，由于深度学习技术的显著改进而导致准确性显著提高的任务示例。这个列表并不全面。在未来的几个月和年份中，进展的速度无疑将继续。

机器学习任务	代表性深度学习技术	我们在本书中使用 TensorFlow.js 执行类似任务的地方
图像内容分类	深度卷积神经网络（卷积网络）如 ResNet^([a]) 和 Inception^([b]) 将 ImageNet 分类任务的错误率从 2011 年的约 25%降至 2017 年的不到 5%。^([c])	为 MNIST 训练卷积网络（第四章）；MobileNet 推断和迁移学习（第五章)
本地化对象和图像	深度卷积网络的变体^([d])将 2012 年的定位误差从 0.33 减少到 2017 年的 0.06。	在 TensorFlow.js 中使用 YOLO (section 5.2)
将一种自然语言翻译成另一种自然语言	Google 的神经机器翻译（GNMT）相比于最佳传统机器翻译技术减少了约 60%的翻译错误。^([e])	基于长短期记忆（LSTM）的序列到序列模型与注意力机制（第九章)
大词汇量连续语音识别	基于 LSTM 的编码器-注意力-解码器架构比最佳非深度学习语音识别系统具有更低的词错误率。^([f])	基于注意力的 LSTM 小词汇量连续语音识别（第九章)
生成逼真图像	生成对抗网络（GANs）现在能够根据训练数据生成逼真的图像（参见github.com/junyanz/CycleGAN）。	使用变分自编码器（VAEs）和 GANs 生成图像（第九章）
生成音乐	循环神经网络（RNNs）和变分自编码器（VAEs）正在帮助创作音乐乐谱和新颖的乐器声音（参见magenta.tensorflow.org/demos）。	训练 LSTMs 生成文本（第九章）
学习玩游戏	深度学习结合强化学习（RL）使机器能够学习使用原始像素作为唯一输入来玩简单的雅达利游戏。^([g]) 结合深度学习和蒙特卡洛树搜索，Alpha-Zero 纯粹通过自我对弈达到了超人类水平的围棋水平。^([h])	使用 RL 解决杆-极控制问题和一个贪吃蛇视频游戏（第十一章）
使用医学图像诊断疾病	深度卷积网络能够根据患者视网膜图像诊断糖尿病视网膜病变，其特异性和敏感性与训练有素的人类眼科医生相当。^([i])	使用预训练的 MobileNet 图像模型进行迁移学习（第五章）。

^a

Kaiming He 等人，“深度残差学习用于图像识别”，IEEE 计算机视觉与模式识别会议 (CVPR)论文集，2016 年，第 770–778 页，mng.bz/PO5P。

^b

Christian Szegedy 等人，“使用卷积进一步深入”，IEEE 计算机视觉与模式识别会议 (CVPR)论文集，2015 年，第 1–9 页，mng.bz/JzGv。

^c

2017 年大规模视觉识别挑战（ILSVRC2017）结果，image-net.org/challenges/LSVRC/2017/results。

^d

Yunpeng Chen 等人，“双路径网络”，arxiv.org/pdf/1707.01629.pdf。

^e

Yonghui Wu 等人，“谷歌的神经机器翻译系统：弥合人机翻译差距”，提交于 2016 年 9 月 26 日，arxiv.org/abs/1609.08144。

^f

Chung-Cheng Chiu 等人，“基于序列到序列模型的最新语音识别技术”，提交于 2017 年 12 月 5 日，arxiv.org/abs/1712.01769。

^g

Volodymyr Mnih 等人，“使用深度强化学习玩雅达利游戏”，2013 年 NIPS 深度学习研讨会，arxiv.org/abs/1312.5602。

^h

David Silver 等人，“通过自我对弈用通用强化学习算法掌握国际象棋和将棋”，提交于 2017 年 12 月 5 日，arxiv.org/abs/1712.01815。

^i

Varun Gulshan 等人，“开发和验证用于检测视网膜底片中糖尿病视网膜病变的深度学习算法”，《JAMA》，第 316 卷，第 22 期，2016 年，第 2402–2410 页，mng.bz/wlDQ。

JavaScript 是一种传统上用于创建 Web 浏览器 UI 和后端业务逻辑（使用 Node.js）的语言。作为一个在 JavaScript 中表达想法和创造力的人，您可能会对深度学习革命感到有些被排斥，因为它似乎是 Python、R 和 C++等语言的专属领域。本书旨在通过名为 TensorFlow.js 的 JavaScript 深度学习库将深度学习和 JavaScript 结合起来。我们这样做是为了让像您这样的 JavaScript 开发人员学会如何编写深度神经网络而不需要学习一门新的语言；更重要的是，我们相信深度学习和 JavaScript 是一对天生的组合。

交叉汇合将创造独特的机会，这是任何其他编程语言都无法提供的。对 JavaScript 和深度学习都是如此。通过 JavaScript，深度学习应用可以在更多平台上运行，触及更广泛的受众，并变得更具视觉和交互性。通过深度学习，JavaScript 开发人员可以使他们的 Web 应用程序更加智能。我们将在本章后面描述如何做到这一点。

表 1.1 列出了迄今为止在这场深度学习革命中我们所见过的一些最令人兴奋的成就。在本书中，我们选择了其中一些应用，并创建了如何在 TensorFlow.js 中实现它们的示例，无论是完整形式还是简化形式。这些示例将在接下来的章节中深入介绍。因此，你不仅仅会对这些突破感到惊叹：你还可以学习它们、理解它们，并在 JavaScript 中实现它们。

但在您深入研究这些令人兴奋的、实用的深度学习示例之前，我们需要介绍有关人工智能、深度学习和神经网络的基本背景。

1.1. 人工智能、机器学习、神经网络和深度学习

AI、机器学习、神经网络和深度学习等短语意味着相关但不同的事物。为了在令人眼花缭乱的人工智能世界中找到方向，您需要了解它们指代的内容。让我们定义这些术语及其之间的关系。

1.1.1. 人工智能

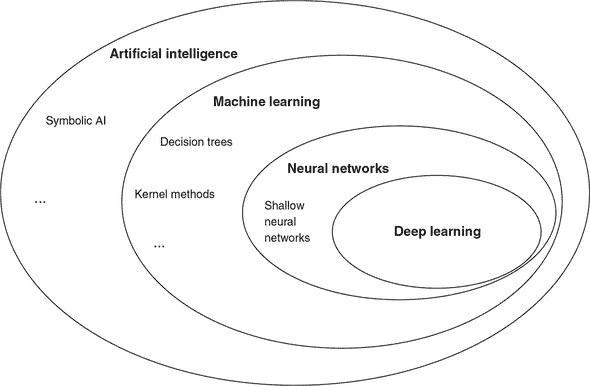
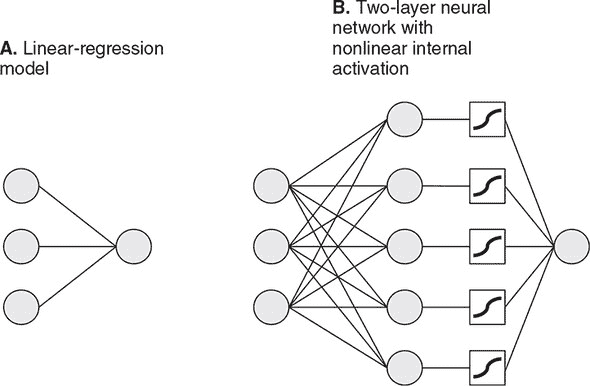
如图 1.1 中的维恩图所示，人工智能是一个广泛的领域。该领域的简明定义如下：自动执行通常由人类执行的智力任务的努力。因此，人工智能涵盖了机器学习、神经网络和深度学习，但它还包括许多与机器学习不同的方法。例如，早期的国际象棋程序涉及由程序员精心制定的硬编码规则。这些不被视为机器学习，因为机器是明确地编程来解决问题，而不是允许它们通过从数据中学习来发现解决问题的策略。很长一段时间以来，许多专家相信通过手工制作一套足够庞大的明确规则来操纵知识并做出决策，可以实现人类级别的人工智能。这种方法被称为符号人工智能，并且它是从 1950 年代到 1980 年代末人工智能的主导范式。^([1])

¹

一个重要的符号人工智能类型是专家系统。请参阅这篇 Britannica 文章了解它们。

图 1.1. 人工智能、机器学习、神经网络和深度学习之间的关系。正如这个维恩图所示，机器学习是人工智能的一个子领域。人工智能的一些领域使用与机器学习不同的方法，如符号人工智能。神经网络是机器学习的一个子领域。存在非神经网络的机器学习技术，如决策树。深度学习是创建和应用“深度”神经网络的科学与艺术——多“层”的神经网络——与“浅层”神经网络——层次较少的神经网络相对。

1.1.2. 机器学习：它与传统编程的不同之处

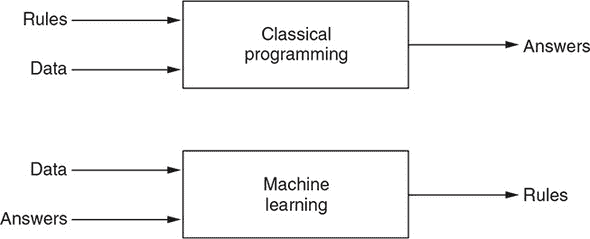
作为与符号人工智能不同的人工智能子领域，机器学习是从一个问题中产生的：计算机是否能超越程序员所知道的如何编程来执行，并且自行学习如何执行特定任务？正如你所看到的，机器学习的方法与符号人工智能的方法根本不同。而符号人工智能依赖于硬编码的知识和规则，机器学习则试图避免这种硬编码。那么，如果一台计算机没有明确指示如何执行任务，它将如何学习如何执行任务呢？答案是通过从数据中学习示例。

这打开了一个新的编程范式（图 1.2）。举个机器学习范例，假设你正在开发一个处理用户上传照片的 Web 应用程序。你希望应用程序的一个功能是自动将照片分类为包含人脸和不包含人脸的照片。应用程序将针对人脸图像和非人脸图像采取不同的操作。为此，你想创建一个程序，在给定任何输入图像（由像素数组组成）时输出二进制的人脸/非人脸答案。

图 1.2. 比较传统编程范式和机器学习范式

我们人类可以在一瞬间完成这个任务：我们大脑的基因硬编码和生活经验赋予了我们这样做的能力。然而，对于任何程序员来说，无论多么聪明和经验丰富，都很难用编程语言（人类与计算机交流的唯一实用方式）编写出如何准确判断图像是否包含人脸的一套明确规则。你可以花费几天的时间查看对 RGB（红绿蓝）像素值进行算术运算的代码，以便检测看起来像脸、眼睛和嘴巴的椭圆轮廓，以及设计关于轮廓之间几何关系的启发式规则。但你很快会意识到，这样的努力充满了难以证明的逻辑和参数的任意选择。更重要的是，很难让它工作得好！^([2]) 你想出的任何启发式方法在面对现实生活图像中人脸可能呈现的各种变化时都很可能不够用，比如脸部的大小、形状和细节的差异；面部表情；发型；肤色；方向；部分遮挡的存在或不存在；眼镜；光照条件；背景中的物体；等等。

²

实际上，以前确实尝试过这样的方法，但效果并不好。这份调查报告提供了深度学习出现之前人脸检测的手工制定规则的很好的例子：Erik Hjelmås 和 Boon Kee Low，“Face Detection: A Survey”，计算机视觉与图像理解，2001 年 9 月，第 236–274 页，mng.bz/m4d2。

在机器学习范式中，你意识到为这样的任务手工制定一套规则是徒劳的。相反，你找到一组图像，其中一些有脸，一些没有。然后，你为每个图像输入期望的（即正确的）脸部或非脸部答案。这些答案被称为标签。这是一个更容易处理的（事实上，微不足道的）任务。如果图像很多，可能需要一些时间来为它们标记标签，但是标记任务可以分配给几个人，并且可以并行进行。一旦你标记了图像，你就应用机器学习，让机器自己发现一套规则。如果你使用正确的机器学习技术，你将得到一套训练有素的规则，能够以超过 99% 的准确率执行脸部/非脸部任务——远远优于任何你希望通过手工制定规则实现的东西。

从前面的例子中，我们可以看到机器学习是自动发现解决复杂问题规则的过程。这种自动化对于像面部检测这样的问题非常有益，人类直觉地知道规则并且可以轻松标记数据。对于其他问题，规则并不是直观的。例如，考虑预测用户是否会点击网页上显示的广告的问题，给定页面和广告的内容以及时间和位置等其他信息。一般来说，没有人能准确预测这种问题。即使有人能够，模式也可能随着时间和新内容、新广告的出现而变化。但是标记的训练数据来自广告服务的历史：它来自广告服务器的日志。仅凭数据和标签的可用性就使机器学习成为解决这类问题的良好选择。

在图 1.3 中，我们更详细地探讨了机器学习涉及的步骤。有两个重要阶段。第一个是训练阶段。这个阶段使用数据和答案，称为训练数据。每对输入数据和期望的答案被称为例子。借助这些例子，训练过程产生了自动发现的规则。尽管规则是自动发现的，但它们并不是完全从零开始发现的。换句话说，机器学习算法并不创造性地提出规则。特别是，人类工程师在训练开始时提供规则的蓝图。这个蓝图被封装在一个模型中，形成了机器可能学习的规则的假设空间。如果没有这个假设空间，就会有一个完全不受限制的、无限的可能规则搜索空间，这不利于在有限的时间内找到好的规则。我们将详细描述可用的模型种类以及根据手头的问题选择最佳模型的方法。目前，可以说，在深度学习的背景下，模型在神经网络由多少层、它们是什么类型的层以及它们如何连接方面有所不同。

图 1.3. 比图 1.2 中更详细的机器学习范式视角。机器学习的工作流程包括两个阶段：训练和推断。训练是机器自动发现将数据转换为答案的规则的过程。学习到的规则被封装在一个经过训练的“模型”中，是训练阶段的成果，并构成推断阶段的基础。推断意味着使用模型为新数据获取答案。

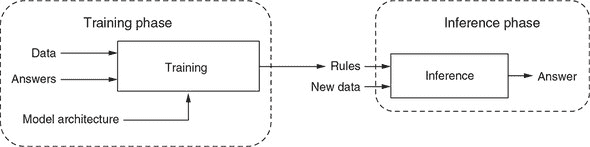
使用训练数据和模型架构，训练过程会产生学习到的规则，封装在一个训练模型中。 这个过程采用蓝图，并以各种方式改变（或调整）它，使模型的输出逐渐接近期望的输出。 训练阶段的时间可以从毫秒到数天不等，这取决于训练数据的数量，模型架构的复杂性以及硬件的速度。 这种机器学习风格——即使用标记的示例逐渐减少模型输出中的错误——被称为监督学习。[3] 本书中涵盖的大部分深度学习算法都是监督学习。 一旦我们有了训练好的模型，就可以将学到的规则应用到新数据上——即训练过程从未见过的数据。 这是第二阶段，或推断阶段。 推断阶段的计算负荷比训练阶段小，因为 1）推断通常一次只处理一个输入（例如，一个图像），而训练涉及遍历所有训练数据； 2）在推断期间，模型不需要被改变。

³

另一种机器学习的风格是无监督学习，其中使用未标记的数据。 无监督学习的例子包括聚类（发现数据集中的不同子集）和异常检测（确定给定示例与训练集中的示例是否足够不同）。

学习数据的表示

机器学习是关于从数据中学习的。 但究竟学到了什么？ 答案：一种有效地转换数据的方式，或者换句话说，将数据的旧表示改变为一个新表示，使我们更接近解决手头的问题。

在我们进一步讨论之前，什么是表示？其核心是一种看待数据的方式。 相同的数据可以以不同的方式来看待，从而导致不同的表示。 例如，彩色图像可以有 RGB 或 HSV（色相-饱和度-值）编码。 这里，编码 和 表示 这两个词基本上是指相同的事物，可以互换使用。 当以这两种不同格式进行编码时，代表像素的数值完全不同，即使它们是同一图像的。 不同的表示对于解决不同的问题非常有用。 例如，要找出图像中所有红色部分，RGB 表示更有用； 但是要找出相同图像的色饱和部分，HSV 表示更有用。 这基本上就是机器学习的全部内容：找到一种适当的转换，将输入数据的旧表示转换为一个新表示——这个新表示适合解决特定的任务，比如在图像中检测汽车的位置或决定图像中是否包含猫和狗。

为了给出一个视觉示例，我们在一个平面上有一组白点和几个黑点（图 1.4）。假设我们想要开发一个算法，可以接受点的二维（x，y）坐标并预测该点是黑色还是白色。在这种情况下，

• 输入数据是点的二维笛卡尔坐标（x 和 y）。

• 输出是点的预测颜色（是黑色还是白色）。

图 1.4. 机器学习的表示转换的玩具示例。面板 A：平面中由黑点和白点组成的数据集的原始表示。面板 B 和 C：两个连续的转换步骤将原始表示转换为更适合颜色分类任务的表示。

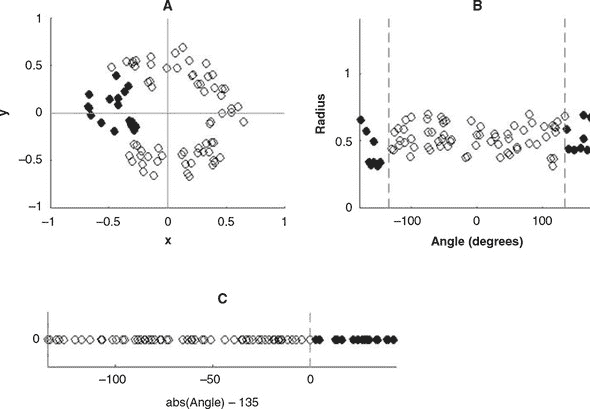
数据显示了图 1.4 的面板 A 中的模式。机器如何根据 x 和 y 坐标决定点的颜色呢？它不能简单地将 x 与一个数字进行比较，因为白点的 x 坐标范围与黑点的 x 坐标范围重叠！同样，算法不能依赖于 y 坐标。因此，我们可以看到点的原始表示不适合黑白分类任务。

我们需要的是一种将两种颜色分开的新表示方式。在这里，我们将原始的笛卡尔 x-y 表示转换为极坐标系统表示。换句话说，我们通过以下方式表示一个点：1）它的角度——x 轴和连接原点与点的线之间形成的角度（参见图 1.4 的面板 A 中的示例）和 2）它的半径——它到原点的距离。经过这个转换，我们得到了相同数据集的新表示，如图 1.4 的面板 B 所示。这个表示更适合我们的任务，因为黑点和白点的角度值现在完全不重叠。然而，这种新的表示仍然不是理想的，因为黑白颜色分类不能简单地与阈值值（如零）进行比较。

幸运的是，我们可以应用第二个转换来实现这一点。这个转换基于简单的公式

(absolute value of angle) - 135 degrees

结果表示，如面板 C 所示，是一维的。与面板 B 中的表示相比，它舍弃了关于点到原点的距离的无关信息。但它是一个完美的表示，因为它允许完全直接的决策过程：

if the value < 0, the point is classified as white;
     else, the point is classified as black

在这个示例中，我们手动定义了数据表示的两步转换。但是，如果我们尝试使用关于正确分类百分比的反馈来自动搜索不同可能的坐标转换，那么我们就会进行机器学习。在解决实际机器学习问题时涉及的转换步骤数量通常远远大于两步，特别是在深度学习中，可以达到数百步。此外，实际机器学习中所见到的表示转换类型可能比这个简单示例中所见到的要复杂得多。深度学习中的持续研究不断发现更复杂、更强大的转换方式。但是，图 1.4 中的示例捕捉到了寻找更好表示的本质。这适用于所有的机器学习算法，包括神经网络、决策树、核方法等。

1.1.3. 神经网络与深度学习

神经网络是机器学习的一个子领域，其中数据表示的转换是由一个系统完成的，其架构 loosely 受到人类和动物大脑中神经元连接方式的启发。神经元在大脑中如何连接到彼此？这在物种和脑区之间有所不同。但是神经元连接的一个经常遇到的主题是层组织。许多哺乳动物的大脑部分都是以分层方式组织的。例如视网膜、大脑皮层和小脑皮层。

至少在表面上，这种模式在某种程度上与人工神经网络的一般组织方式相似（在计算机领域简称为神经网络，这里几乎没有混淆的风险），其中数据在多个可分隔阶段中进行处理，适当地称为层。这些层通常被堆叠在一起，仅在相邻层之间存在连接。图 1.5 显示了一个具有四层的简单（人工）神经网络。输入数据（在本例中为图像）流入第一层（图中的左侧），然后依次从一层流向下一层。每个层对数据的表示应用新的转换。随着数据通过层的流动，表示与原始数据越来越不同，并且越来越接近神经网络的目标，即为输入图像应用正确的标签。最后一层（图中的右侧）发出神经网络的最终输出，即图像分类任务的结果。

图 1.5. 神经网络的示意图，按层组织。这个神经网络对手写数字的图像进行分类。在层之间，你可以看到原始数据的中间表示。经授权转载自 François Chollet 的《用 Python 进行深度学习》，Manning 出版社，2017 年。

神经网络的一层类似于一个数学函数，因为它是从输入值到输出值的映射。然而，神经网络的层与纯粹的数学函数不同，因为它们通常是有状态的。换句话说，它们持有内部记忆。一个层的记忆体现在它的权重中。什么是权重？它们只是一组属于该层的数值，决定了每个输入表示在该层如何被转换为输出表示。例如，常用的密集层通过将其输入数据与矩阵相乘，并将结果加上一个向量来进行转换。矩阵和向量就是密集层的权重。当一个神经网络通过接触训练数据进行训练时，权重会以一种系统化的方式发生变化，目的是最小化一个称为损失函数的特定值，我们将在第二章和第三章中通过具体例子详细介绍这一点。

尽管神经网络的灵感来源于大脑，但我们应该小心不要过度赋予它们人性化。神经网络的目的是不是研究或模拟大脑的工作方式。这是神经科学的领域，是一个独立的学术学科。神经网络的目的是通过从数据中学习，让机器执行有趣的实际任务。虽然一些神经网络在结构和功能上与生物大脑的某些部分相似，确实值得注意，但这是否只是巧合超出了本书的范围。无论如何，我们不应过度解读这些相似性。重要的是，没有证据表明大脑是通过任何形式的梯度下降学习的，而梯度下降是训练神经网络的主要方式（在下一章中介绍）。许多神经网络中的重要技术帮助推动了深度学习革命，它们的发明和采用并不是因为得到了神经科学的支持，而是因为它们帮助神经网络更好、更快地解决实际学习任务。

⁴

关于功能相似性的一个引人注目的例子，请看那些最大化激活卷积神经网络不同层的输入（参见第四章），这些输入与人类视觉系统不同部分的神经元感受野有着密切的相似之处。

现在你知道什么是神经网络了，我们可以告诉你什么是深度学习。深度学习是研究和应用深度神经网络的学科，简单地说，就是具有许多层次（通常是从几十到数百层）的神经网络。在这里，深度一词指的是大量连续层次的表示法的概念。构成数据模型的层数称为模型的深度。该领域的其他合适名称可能是“层次表示学习”或“分层表示学习”。现代深度学习通常涉及数十到数百个连续的表示层次，它们都是自动从训练数据中学习的。与此同时，其他机器学习方法往往集中于仅学习一到两层数据表示；因此，它们有时被称为浅层学习。

在深度学习中，“深度”一词被误解为对数据的任何深层次理解，即，“深度”意味着理解像“自由不是免费的”这样的句子背后的含义，或者品味 M.C. Escher 的作品中的矛盾和自指。这种“深度”对于人工智能研究者来说仍然是一个难以捉摸的目标。[5]未来，深度学习可能会让我们更接近这种深度，但这肯定比给神经网络添加层次更难量化和实现。

⁵

Douglas Hofstadter，《Google 翻译的浅薄》，《大西洋月刊》，2018 年 1 月 30 日，mng.bz/5AE1。

不仅仅是神经网络：其他流行的机器学习技术

我们直接从 图 1.1 的 Venn 图中的“机器学习”圈子转到内部的“神经网络”圈子。然而，值得我们简要讨论一下不是神经网络的机器学习技术，不仅因为这样做会给我们更好的历史背景，而且因为您可能会在现有代码中遇到一些这样的技术。

朴素贝叶斯分类器是最早的机器学习形式之一。简而言之，贝叶斯定理是关于如何估计事件概率的定理，给定 1) 事件发生的先验信念有多大可能性和 2) 与事件相关的观察事实（称为特征）。这个定理可以用来通过选择给定观察事实的最大概率（似然）的类别，将观察到的数据点分类到许多已知类别之一。朴素贝叶斯基于观察到的事实相互独立的假设（一个强假设和天真的假设，因此得名）。

逻辑回归（或 logreg）也是一种分类技术。由于它的简单和多才多艺的性质，它仍然很受欢迎，通常是数据科学家在尝试了解手头分类任务的感觉后尝试的第一件事情。

核方法，其中支持向量机（SVM）是最著名的例子，通过将原始数据映射到更高维度的空间，并找到一个最大化两类示例之间距离（称为边距）的转换来解决二元（即两类）分类问题。

决策树是类似流程图的结构，允许您对输入数据点进行分类或根据输入预测输出值。在流程图的每个步骤中，您需要回答一个简单的是/否问题，例如，“特征 X 是否大于某个阈值？”根据答案是是还是否，您将前进到两个可能的下一个问题之一，这只是另一个是/否问题，依此类推。一旦到达流程图的末尾，您将得到最终答案。因此，决策树易于人类可视化和解释。

随机森林和梯度提升机通过形成大量专门的个体决策树的集成来提高决策树的准确性。集成，也称为集成学习，是训练一组（即集成）个体机器学习模型并在推理过程中使用它们的输出的技术。如今，梯度提升可能是处理非感知数据（例如，信用卡欺诈检测）的最佳算法之一，如果不是最佳算法。与深度学习并列，它是数据科学竞赛（例如 Kaggle 上的竞赛）中最常用的技术之一。

神经网络的兴起、衰退和再兴起，以及背后的原因

神经网络的核心思想早在 1950 年代就形成了。训练神经网络的关键技术，包括反向传播，是在 1980 年代发明的。然而，在 1980 年代到 2010 年代的很长一段时间里，神经网络几乎完全被研究界忽视，部分原因是由于竞争方法（如 SVM）的流行，部分原因是由于缺乏训练深度（多层）神经网络的能力。但是大约在 2010 年左右，一些仍然在研究神经网络的人开始取得重要的突破：加拿大多伦多大学的 Geoffrey Hinton 小组，蒙特利尔大学的 Yoshua Bengio 小组，纽约大学的 Yann LeCun 小组，以及瑞士达勒莫勒人工智能研究所（IDSIA）的研究人员。这些团队取得了重要的里程碑，包括在图形处理单元（GPU）上实现深度神经网络的第一个实际应用，并将 ImageNet 计算机视觉挑战的错误率从约 25%降低到不到 5%。

自 2012 年以来，深度卷积神经网络（卷积网络）已成为所有计算机视觉任务的首选算法；更一般地，它们适用于所有感知任务。非计算机视觉感知任务的例子包括语音识别。在 2015 年和 2016 年的主要计算机视觉会议上，几乎不可能找到不涉及卷积网络的演示。同时，深度学习还在许多其他类型的问题中找到了应用，如自然语言处理。它已经完全取代了支持向量机（SVM）和决策树在广泛应用的范围内。例如，多年来，欧洲核子研究组织（CERN）使用基于决策树的方法来分析大型强子对撞机中的 ATLAS 探测器的粒子数据；但由于其在大型数据集上的性能更高且更容易训练，CERN 最终转向了深度神经网络。

那么，是什么让深度学习在众多可用的机器学习算法中脱颖而出呢？（请参阅信息框 1.1 查看一些不是深度神经网络的流行机器学习技术列表。）深度学习迅速崛起的主要原因之一是它在许多问题上提供了更好的性能。但这并不是唯一的原因。深度学习还使问题解决变得更容易，因为它自动化了曾经是机器学习工作流程中最关键和最困难的步骤：特征工程。

以前的机器学习技术——浅层学习——只涉及将输入数据转换为一个或两个连续的表示空间，通常通过简单的转换，如高维非线性投影（核方法）或决策树。但是，复杂问题所需的精细表示通常无法通过这些技术获得。因此，人工工程师不得不费尽心思地使初始输入数据更容易被这些方法处理：他们不得不手动为其数据设计出良好的表示层。这就是特征工程。另一方面，深度学习自动化了这一步骤：通过深度学习，您可以一次学习所有特征，而不是自己设计它们。这极大地简化了机器学习工作流程，通常用单个、简单的端到端深度学习模型替代了复杂的多阶段管道。通过自动化特征工程，深度学习使机器学习变得更少劳动密集和更加健壮——一举两得。

这是深度学习从数据中学习的两个基本特征：逐层增量地开发越来越复杂的表示方式；以及这些中间增量表示是共同学习的，每层都更新以满足其上层和下层的表示需求。这两个属性共同使深度学习比以前的机器学习方法更加成功。

1.1.4. 为什么深度学习？为什么是现在？

如果神经网络的基本思想和核心技术早在 1980 年代就已存在，为什么深度学习革命直到 2012 年才开始发生？两者之间发生了什么变化？总的来说，推动机器学习进步的有三个技术力量：

• 硬件

• 数据集和基准测试

• 算法进展

让我们逐一探讨这些因素。

硬件

深度学习是一门由实验结果指导而非理论指导的工程科学。只有当适当的硬件可用于尝试新的想法（或扩大旧想法的规模，通常情况下）时，算法进展才能成为可能。用于计算机视觉或语音识别的典型深度学习模型所需的计算能力比您的笔记本电脑提供的数量级更高。

在整个 21 世纪的头十年中，NVIDIA 和 AMD 等公司投入了数十亿美元开发快速、大规模并行芯片——用于提供越来越逼真的视频游戏图形的单一用途超级计算机，旨在实时在您的屏幕上渲染复杂的 3D 场景。当 NVIDIA 于 2007 年推出 CUDA（短语 Compute Unified Device Architecture）时，这些投资开始让科学界受益。CUDA 是其 GPU 产品线的通用编程接口。在各种高度可并行化的应用程序中，一小部分 GPU 开始取代大型 CPU 集群，从物理建模开始。由许多矩阵乘法和加法组成的深度神经网络也是高度可并行化的。

在 2011 年左右，一些研究人员开始编写神经网络的 CUDA 实现，丹·希雷赞和亚历克斯·克里兹弗斯基是其中的先驱之一。如今，高端 GPU 在训练深度神经网络时可以提供比 typical CPU 高出数百倍的并行计算能力。如果没有现代 GPU 的强大计算能力，许多最先进的深度神经网络的训练是不可能的。

数据和基准测试

如果硬件和算法是深度学习革命的蒸汽机，那么数据就是它的煤炭：是驱动我们智能机器的原材料，没有它什么也不可能。在数据方面，除了过去 20 年存储硬件的指数级进步（遵循摩尔定律）之外，游戏变革者是互联网的崛起，使得收集和分发用于机器学习的大型数据集成为可能。今天，大型公司处理图像数据集、视频数据集和自然语言数据集，而这些数据集没有互联网是无法收集的。Flickr 上用户生成的图像标签，例如，已成为计算机视觉的数据宝库。YouTube 视频也是如此。而维基百科是自然语言处理的关键数据集。

如果有一个数据集促进了深度学习的崛起，那就是 ImageNet，它由 140 万张手动注释的图片组成，涵盖 1000 个分类。使 ImageNet 特殊的不仅仅是其规模庞大；还有与之相关的年度比赛。自 2010 年以来，像 ImageNet 和 Kaggle 这样的公开竞赛是激励研究人员和工程师去突破极限的极佳方式。拥有共同的基准让研究人员竞争超越已经极大地推动了深度学习的最近崛起。

算法进步

除了硬件和数据之外，在 2000 年代后期之前，我们还缺乏一种可靠的方法来训练非常深的神经网络。因此，神经网络仍然是相当浅的，只使用一两层表示；因此，它们无法与更精细的浅层方法（如 SVM 和随机森林）相媲美。关键问题在于通过深层堆栈的层传播梯度。用于训练神经网络的反馈信号会随着层数的增加而减弱。

这种情况在 2009 年至 2010 年发生了变化，随着几个简单但重要的算法改进的出现，使梯度传播变得更好：

• 更好的激活函数用于神经网络层（如线性整流单元，或 relu）

• 更好的权重初始化方案（例如，Glorot 初始化）

• 更好的优化方案（例如，RMSProp 和 ADAM 优化器）

只有当这些改进开始允许训练具有 10 层或更多层的模型时，深度学习才开始发光发热。最终，在 2014 年、2015 年和 2016 年，还发现了更先进的帮助梯度传播的方法，如批归一化、残差连接和深度可分离卷积。今天，我们可以从头开始训练数千层深的模型。

1.2. 为什么要结合 JavaScript 和机器学习？

机器学习，像人工智能和数据科学的其他分支一样，通常使用传统的后端语言进行，比如 Python 和 R，运行在服务器或工作站上而不是在 web 浏览器中。^([6]) 这种现状并不令人意外。深度神经网络的训练通常需要多核和 GPU 加速的计算，这在浏览器选项卡中直接不可用；有时需要大量数据来训练这样的模型，最方便的方式是在后端进行摄取：例如，从几乎无限大小的本地文件系统中。直到最近，许多人认为“JavaScript 中的深度学习”是一种新奇事物。在本节中，我们将阐述为什么对于许多种类的应用来说，在浏览器环境中使用 JavaScript 进行深度学习是一个明智的选择，并解释如何结合深度学习和 web 浏览器的力量创造独特的机会，特别是在 TensorFlow.js 的帮助下。

⁶

Srishti Deoras，“数据科学家学习的前 10 种编程语言”，《Analytics India Magazine》，2018 年 1 月 25 日，mng.bz/6wrD。

首先，一旦训练了机器学习模型，就必须将其部署到某个地方，以便对真实数据进行预测（例如对图像和文本进行分类，检测音频或视频流中的事件等）。没有部署，对模型进行训练只是浪费计算资源。通常情况下，希望或必须将“某个地方”设置为 web 前端。本书的读者可能会意识到 web 浏览器的整体重要性。在台式机和笔记本电脑上，通过 web 浏览器是用户访问互联网上的内容和服务的主要方式。这是用户在使用这些设备时花费大部分时间的方式，远远超过第二名。这是用户完成大量日常工作、保持联系和娱乐自己的方式。运行在 web 浏览器中的各种应用程序为应用客户端机器学习提供了丰富的机会。对于移动前端来说，Web 浏览器在用户参与度和时间上落后于原生移动应用程序。但是，移动浏览器仍然是一股不可忽视的力量，因为它们具有更广泛的覆盖范围、即时访问和更快的开发周期。^([7]) 实际上，由于它们的灵活性和易用性，许多移动应用程序，例如 Twitter 和 Facebook，对于某些类型的内容会在启用 JavaScript 的 web 视图中运行。

⁷

Rishabh Borde，“移动应用中花费在互联网上的时间，2017–19：比移动网络多了 8 倍”，DazeInfo，2017 年 4 月 12 日，mng.bz/omDr。

由于其广泛的覆盖范围，Web 浏览器是部署深度学习模型的一个合理选择，只要模型所需的数据类型在浏览器中可用。但是，浏览器中有哪些类型的数据可用呢？答案是，很多！例如，深度学习的最流行应用：图像和视频中的对象分类和检测、语音转录、语言翻译和文本内容分析。Web 浏览器配备了可能是最全面的技术和 API，用于呈现（以及在用户许可的情况下捕获）文本、图像、音频和视频数据。因此，强大的机器学习模型可以直接在浏览器中使用，例如，使用 TensorFlow.js 和简单的转换过程。在本书的后几章中，我们将涵盖许多在浏览器中部署深度学习模型的具体示例。例如，一旦您从网络摄像头捕获了图像，您可以使用 TensorFlow.js 运行 MobileNet 对对象进行标记，运行 YOLO2 对检测到的对象放置边界框，运行 Lipnet 进行唇读，或者运行 CNN-LSTM 网络为图像应用标题。

一旦您使用浏览器的 WebAudio API 从麦克风捕获了音频，TensorFlow.js 就可以运行模型执行实时口语识别。文本数据也有令人兴奋的应用，例如为用户文本（如电影评论）分配情感分数（第九章）。除了这些数据模态，现代 Web 浏览器还可以访问移动设备上的一系列传感器。例如，HTML5 提供了对地理位置（纬度和经度）、运动（设备方向和加速度）和环境光（参见 mobilehtml5.org）的 API 访问。结合深度学习和其他数据模态，来自这些传感器的数据为许多令人兴奋的新应用打开了大门。

基于浏览器的深度学习应用具有五个额外的好处：降低服务器成本、减少推理延迟、数据隐私、即时 GPU 加速和即时访问：

• 服务器成本在设计和扩展 Web 服务时通常是一个重要考虑因素。及时运行深度学习模型所需的计算通常是相当大的，这就需要使用 GPU 加速。如果模型没有部署到客户端，它们就需要部署在支持 GPU 的机器上，比如来自 Google Cloud 或 Amazon Web Services 的具有 CUDA GPU 的虚拟机。这样的云 GPU 机器通常价格昂贵。即使是最基本的 GPU 机器目前也在每小时约$0.5–1 左右（见 www.ec2instances.info 和 cloud.google.com/gpu）。随着流量的增加，运行一系列云 GPU 机器的成本变得更高，更不用说可伸缩性的挑战以及服务器堆栈的复杂性。所有这些问题都可以通过将模型部署到客户端来消除。客户端下载模型的开销（通常是数兆字节或更多）可以通过浏览器的缓存和本地存储功能来减轻（第二章）。

• 降低推理延迟—对于某些类型的应用程序，延迟的要求非常严格，以至于深度学习模型必须在客户端上运行。任何涉及实时音频、图像和视频数据的应用程序都属于此类。考虑一下如果图像帧需要传输到服务器进行推理会发生什么。假设图像以每秒 10 帧的速率从摄像头捕获，大小适中为 400 × 400 像素，具有三个颜色通道（RGB）和每个颜色通道 8 位深度。即使使用 JPEG 压缩，每个图像的大小也约为 150 Kb。在具有约 300 Kbps 上传带宽的典型移动网络上，每个图像的上传可能需要超过 500 毫秒，导致一个可察觉且可能不可接受的延迟，对于某些应用程序（例如游戏）来说。这个计算没有考虑到网络连接的波动（和可能的丢失）、下载推理结果所需的额外时间以及大量的移动数据使用量，每一项都可能是一个停滞点。客户端推理通过在设备上保留数据和计算来解决这些潜在的延迟和连接性问题。在没有模型纯粹在客户端上运行的情况下，无法运行实时的机器学习应用程序，比如在网络摄像头图像中标记对象和检测姿势。即使对于没有延迟要求的应用程序，减少模型推理延迟也可以提高响应性，从而改善用户体验。

• 数据隐私——将训练和推断数据留在客户端的另一个好处是保护用户的隐私。数据隐私的话题在今天变得越来越重要。对于某些类型的应用程序，数据隐私是绝对必要的。与健康和医疗数据相关的应用程序是一个突出的例子。考虑一个“皮肤病诊断辅助”应用，它从用户的网络摄像头收集患者皮肤的图像，并使用深度学习生成皮肤状况的可能诊断。许多国家的健康信息隐私法规将不允许将图像传输到集中式服务器进行推断。通过在浏览器中运行模型推断，用户的数据永远不需要离开用户的手机或存储在任何地方，确保用户健康数据的隐私。再考虑另一个基于浏览器的应用程序，它使用深度学习为用户提供建议，以改善他们在应用程序中编写的文本。一些用户可能会使用此应用程序编写诸如法律文件之类的敏感内容，并且不希望数据通过公共互联网传输到远程服务器。在客户端浏览器 JavaScript 中纯粹运行模型是解决此问题的有效方法。

• 即时的 WebGL 加速 — 除了数据可用性外，将机器学习模型在 Web 浏览器中运行的另一个先决条件是通过 GPU 加速获得足够的计算能力。 正如前面提到的，许多最先进的深度学习模型在计算上是如此密集，以至于通过 GPU 上的并行计算加速是必不可少的（除非您愿意让用户等待几分钟才能获得单个推断结果，在真实应用中很少发生）。 幸运的是，现代 Web 浏览器配备了 WebGL API，尽管它最初是为了加速 2D 和 3D 图形的渲染而设计的，但可以巧妙地利用它来进行加速神经网络所需的并行计算。 TensorFlow.js 的作者们费尽心思地将基于 WebGL 的深度学习组件加速包装在库中，因此通过一行 JavaScript 导入即可为您提供加速功能。 基于 WebGL 的神经网络加速可能与本机的、量身定制的 GPU 加速（如 NVIDIA 的 CUDA 和 CuDNN，用于 Python 深度学习库，如 TensorFlow 和 PyTorch）不完全相匹配，但它仍然会大大加快神经网络的速度，并实现实时推断，例如 PoseNet 对人体姿势的提取。 如果对预训练模型进行推断是昂贵的，那么对这些模型进行训练或迁移学习的成本就更高了。 训练和迁移学习使得诸如个性化深度学习模型、前端可视化深度学习和联邦学习（在许多设备上训练相同的模型，然后聚合训练结果以获得良好的模型）等令人兴奋的应用成为可能。 TensorFlow.js 的 WebGL 加速使得在 Web 浏览器中纯粹进行训练或微调神经网络成为可能。

• 即时访问 — 一般来说，运行在浏览器中的应用程序具有“零安装”的天然优势：访问应用程序所需的全部步骤就是输入 URL 或单击链接。 这省去了任何可能繁琐和容易出错的安装步骤，以及在安装新软件时可能存在的风险访问控制。 在浏览器中进行深度学习的背景下，TensorFlow.js 提供的基于 WebGL 的神经网络加速不需要特殊类型的图形卡或为此类卡安装驱动程序，这通常是一个不平凡的过程。 大多数合理更新的台式机、笔记本电脑和移动设备都配备了供浏览器和 WebGL 使用的图形卡。 只要安装了与 TensorFlow.js 兼容的 Web 浏览器（门槛很低），这些设备就可以自动准备好运行 WebGL 加速的神经网络。 这在访问便利至关重要的地方尤为吸引人，例如深度学习的教育。

使用 GPU 和 WebGL 加速计算

训练机器学习模型并将其用于推断需要大量的数学运算。例如，广泛使用的“密集”神经网络层涉及将大矩阵与向量相乘，并将结果添加到另一个向量中。这种类型的典型操作涉及数千或数百万次浮点运算。关于这类操作的一个重要事实是它们通常是可并行化的。例如，将两个向量相加可以分解为许多较小的操作，比如将两个单独的数字相加。这些较小的操作不相互依赖。例如，您不需要知道两个向量在索引 0 处的两个元素的和来计算索引 1 处的两个元素的和。因此，这些较小的操作可以同时进行，而不是一个接一个地进行，无论向量有多大。串行计算，例如向量加法的简单 CPU 实现，被称为单指令单数据（SISD）。GPU 上的并行计算称为单指令多数据（SIMD）。通常，CPU 计算每个单独的加法所需的时间比 GPU 更少。但是，在这么大量的数据上的总成本导致 GPU 的 SIMD 胜过 CPU 的 SISD。深度神经网络可以包含数百万个参数。对于给定的输入，可能需要进行数十亿次逐元素数学运算（如果不是更多）。GPU 能够执行的大规模并行计算在这个规模下表现出色。

任务：逐个元素添加两个向量：

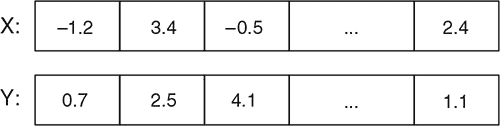
CPU 上的计算

GPU 上的计算

WebGL 加速如何利用 GPU 的并行计算能力来实现比 CPU 更快的向量操作

精确来说，现代 CPU 也能够执行一定级别的 SIMD 指令。但是，GPU 配备了更多的处理单元（数量在数百到数千之间），可以同时对输入数据的多个片段执行指令。向量加法是一个相对简单的 SIMD 任务，因为每个计算步骤只查看一个索引，并且不同索引处的结果彼此独立。在机器学习中看到的其他 SIMD 任务更复杂。例如，在矩阵乘法中，每个计算步骤使用多个索引处的数据，并且索引之间存在依赖关系。但是通过并行化加速的基本思想是相同的。

有趣的是，GPU 最初并不是为加速神经网络而设计的。这可以从名称中看出：图形处理单元。GPU 的主要用途是处理 2D 和 3D 图形。在许多图形应用中，例如 3D 游戏，至关重要的是要尽可能地快速处理，以便屏幕上的图像可以以足够高的帧率更新，以获得流畅的游戏体验。这是 GPU 的创建者利用 SIMD 并行化时的最初动机。但令人惊喜的是，GPU 能够进行的并行计算也正适合机器学习的需求。

用于 GPU 加速的 WebGL 库 TensorFlow.js 最初是为在网络浏览器中渲染 3D 对象上的纹理（表面图案）等任务而设计的。但是，纹理只是一组数字！因此，我们可以假装这些数字是神经网络的权重或激活，并重新利用 WebGL 的 SIMD 纹理操作来运行神经网络。这正是 TensorFlow.js 在浏览器中加速神经网络的方式。

除了我们描述的优势之外，基于网络的机器学习应用享受与不涉及机器学习的通用网络应用相同的好处：

• 与原生应用开发不同，使用 TensorFlow.js 编写的 JavaScript 应用程序将在许多设备系列上运行，从 Mac、Windows 和 Linux 桌面到 Android 和 iOS 设备。

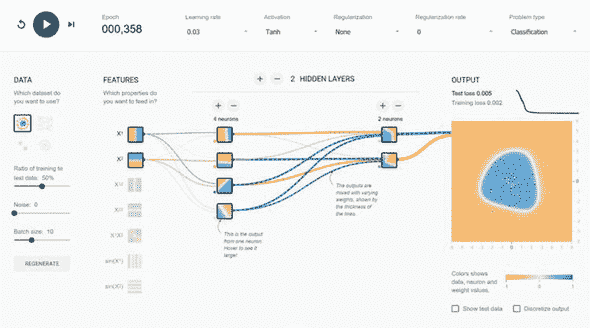
• 凭借其优化的二维和三维图形能力，网络浏览器是数据可视化和交互性最丰富、最成熟的环境。在人们希望向人类展示神经网络的行为和内部机制时，很难想象有哪种环境能比得上浏览器。以 TensorFlow Playground 为例（playground.tensorflow.org）。这是一个非常受欢迎的 Web 应用程序，您可以使用其中与神经网络交互式解决分类问题。您可以调整神经网络的结构和超参数，并观察其隐藏层和输出的变化（见图 1.6）。如果您之前还没有尝试过，我们强烈建议您试试。许多人表示，这是他们在神经网络主题上看到的最具有教育性和愉悦性的教育材料之一。事实上，TensorFlow Playground 实际上是 TensorFlow.js 的重要前身。作为 Playground 的衍生品，TensorFlow.js 具有更广泛的深度学习功能和更优化的性能。此外，它还配备了一个专门用于深度学习模型可视化的组件（在第七章中有详细介绍）。无论您是想构建基本的教育应用程序，还是以视觉上吸引人和直观的方式展示您的前沿深度学习研究，TensorFlow.js 都将帮助您在实现目标的道路上走得更远（参见诸如实时 tSNE 嵌入可视化的示例^([8])）。

  ¹⁰

  参见 Nicola Pezzotti，“使用 TensorFlow.js 进行实时 tSNE 可视化”，googblogs，mng.bz/nvDg。

图 1.6. TensorFlow Playground 的屏幕截图（playground.tensorflow.org），这是一个由谷歌的 Daniel Smilkov 及其同事开发的受欢迎的基于浏览器的用户界面，用于教授神经网络的工作原理。TensorFlow Playground 也是后来 TensorFlow.js 项目的重要前身。

1.2.1. 使用 Node.js 进行深度学习

为了安全和性能考虑，Web 浏览器被设计为资源受限的环境，具有有限的内存和存储配额。这意味着，尽管浏览器对许多类型的推断、小规模训练和迁移学习任务（需要较少的资源）非常理想，但对于使用大量数据训练大型机器学习模型来说，并不是理想的环境。然而，Node.js 完全改变了这一方程。Node.js 使 JavaScript 能够在 Web 浏览器之外运行，从而赋予它对所有本机资源（如 RAM 和文件系统）的访问权限。TensorFlow.js 带有一个 Node.js 版本，称为tfjs-node。它直接绑定到从 C++和 CUDA 代码编译的本机 TensorFlow 库，并且使用户能够使用与 TensorFlow（在 Python 中）底层使用的并行化 CPU 和 GPU 操作内核相同的内核。正如可以通过实证显示的那样，在 tfjs-node 中模型训练的速度与 Python 中 Keras 的速度相当。因此，tfjs-node 是一个适合用于训练大型机器学习模型的环境。在本书中，您将看到一些示例，我们在其中使用 tfjs-node 来训练超出浏览器能力范围的大型模型（例如，第五章中的单词识别器和第九章中的文本情感分析器）。

但是，相对于更成熟的 Python 环境来训练机器学习模型，选择 Node.js 的可能原因是什么呢？答案是 1）性能和 2）与现有堆栈和开发人员技能集的兼容性。首先，在性能方面，如 Node.js 所使用的 V8 引擎等最新 JavaScript 解释器对 JavaScript 代码进行即时（JIT）编译，导致性能优于 Python。因此，只要模型足够小以至于语言解释器的性能成为决定因素，通常在 tfjs-node 中训练模型比在 Keras（Python）中快。

其次，Node.js 是构建服务器端应用程序的非常流行的环境。如果您的后端已经是用 Node.js 编写的，并且您想要向堆栈中添加机器学习，那么使用 tfjs-node 通常比使用 Python 更好。通过保持代码在一个语言中，您可以直接重用代码库的大部分代码，包括加载和格式化数据的那些部分。这将帮助您更快地设置模型训练管道。通过不向堆栈添加新语言，您还可以降低其复杂性和维护成本，可能节省雇佣 Python 程序员的时间和成本。

最后，用 TensorFlow.js 编写的机器学习代码将在浏览器环境和 Node.js 中都能工作，只有在依赖于仅限于浏览器或仅限于 Node 的 API 的数据相关代码可能会有例外。您在本书中遇到的大多数代码示例都将在这两种环境中工作。我们努力将代码中与环境无关且以机器学习为中心的部分与与环境相关的数据摄取和 UI 代码分开。额外的好处是您只需学习一个库，就能在服务器和客户端都进行深度学习。

1.2.2. JavaScript 生态系统

当评估 JavaScript 在某种类型的应用程序（如深度学习）中的适用性时，我们不应忽视 JavaScript 是一种具有异常强大生态系统的语言的因素。多年来，JavaScript 在 GitHub 上的存储库数量和拉取活动方面一直稳居数十种编程语言中的第一位（参见 githut.info）。在 npm 上，JavaScript 包的事实上公共存储库，截至 2018 年 7 月，已经有超过 600,000 个包。这个数字是 PyPI（Python 包的事实上公共存储库）的包数量的四倍以上（参见 www.modulecounts.com）。尽管 Python 和 R 在机器学习和数据科学领域拥有更成熟的社区，但 JavaScript 社区也在建立机器学习相关的数据流水线支持。

想要从云存储和数据库获取数据吗？谷歌云和亚马逊 Web 服务都提供 Node.js API。如今最流行的数据库系统，如 MongoDB 和 RethinkDB，都对 Node.js 驱动程序提供了一流的支持。想要在 JavaScript 中整理数据吗？我们推荐 Ashley Davis 的《使用 JavaScript 进行数据整理》一书（Manning Publications，2018 年，www.manning.com/books/data-wrangling-with-javascript）。想要可视化您的数据吗？有成熟和强大的库，如 d3.js、vega.js 和 plotly.js，在许多方面超越了 Python 可视化库。一旦您准备好输入数据，本书的主要内容 TensorFlow.js 将接手处理，并帮助您创建、训练和执行深度学习模型，以及保存、加载和可视化它们。

最后，JavaScript 生态系统仍在以令人振奋的方式不断发展。它的影响力正在从其传统的强项——即 Web 浏览器和 Node.js 后端环境——扩展到新的领域，例如桌面应用程序（例如 Electron）和本地移动应用程序（例如 React Native 和 Ionic）。对于这样的框架编写 UI 和应用程序通常比使用各种平台特定的应用程序创建工具更容易。JavaScript 是一种具有将深度学习的力量带到所有主要平台的潜力的语言。我们在 table 1.2 中总结了将 JavaScript 和深度学习结合使用的主要优点。

表 1.2. 在 JavaScript 中进行深度学习的利益的简要总结

考虑因素	示例
与客户端相关的原因

• 由于数据局部性而降低推理和训练延迟

• 在客户端脱机时运行模型的能力

• 隐私保护（数据永远不会离开浏览器）

• 降低服务器成本

• 简化的部署栈

|

与 Web 浏览器相关的原因

• 可用于推理和训练的多种数据形式（HTML5 视频、音频和传感器 API）

• 零安装用户体验

• 在广泛范围的 GPU 上通过 WebGL API 进行并行计算的零安装访问

• 跨平台支持

• 理想的可视化和交互环境

• 固有互联环境开启对各种机器学习数据和资源的直接访问

|

与 JavaScript 相关的原因

• JavaScript 是许多衡量标准中最受欢迎的开源编程语言，因此有大量的 JavaScript 人才和热情。

• JavaScript 在客户端和服务器端都有着丰富的生态系统和广泛的应用。

• Node.js 允许应用程序在服务器端运行，而不受浏览器资源约束。

• V8 引擎使 JavaScript 代码运行速度快。

|

1.3. 为什么选择 TensorFlow.js？

要在 JavaScript 中进行深度学习，您需要选择一个库。TensorFlow.js 是我们这本书的选择。在本节中，我们将描述 TensorFlow.js 是什么以及我们选择它的原因。

1.3.1. TensorFlow、Keras 和 TensorFlow.js 的简要历史

TensorFlow.js 是一个使您能够在 JavaScript 中进行深度学习的库。顾名思义，TensorFlow.js 旨在与 Python 深度学习框架 TensorFlow 保持一致和兼容。要了解 TensorFlow.js，我们需要简要介绍 TensorFlow 的历史。

TensorFlow 是由谷歌的深度学习团队于 2015 年 11 月开源的。本书的作者是该团队的成员。自从它开源以来，TensorFlow 受到了极大的欢迎。它现在被广泛应用于谷歌和更大的技术社区中的各种工业应用和研究项目中。名称“TensorFlow”是为了反映使用该框架编写的典型程序内部发生的情况：数据表示称为tensors（张量）在层和其他数据处理节点之间流动，允许对机器学习模型进行推理和训练。

首先，什么是张量？这只是计算机科学家简明扼要地说“多维数组”的方式。在神经网络和深度学习中，每个数据和每个计算结果都表示为一个张量。例如，灰度图像可以表示为一个数字的 2D 数组——一个 2D 张量；彩色图像通常表示为一个 3D 张量，其中额外的维度是颜色通道。声音、视频、文本和任何其他类型的数据都可以表示为张量。每个张量具有两个基本属性：数据类型（例如 float32 或 int32）和形状。形状描述了张量沿着所有维度的大小。例如，一个 2D 张量可能具有形状[128, 256]，而一个 3D 张量可能具有形状[10, 20, 128]。一旦数据被转换为给定数据类型和形状的张量，它就可以被馈送到接受该数据类型和形状的任何类型的层中，而不管数据的原始含义是什么。因此，张量是深度学习模型的通用语言。

但是为什么使用张量？在前一节中，我们了解到在运行深度神经网络中涉及的大部分计算是作为大规模并行化操作执行的，通常在 GPU 上进行，这需要对多个数据块执行相同的计算。张量是将我们的数据组织成可以在并行中高效处理的结构的容器。当我们将形状为[128, 128]的张量 A 加到形状为[128, 128]的张量 B 时，非常清楚需要进行128 * 128次独立的加法运算。

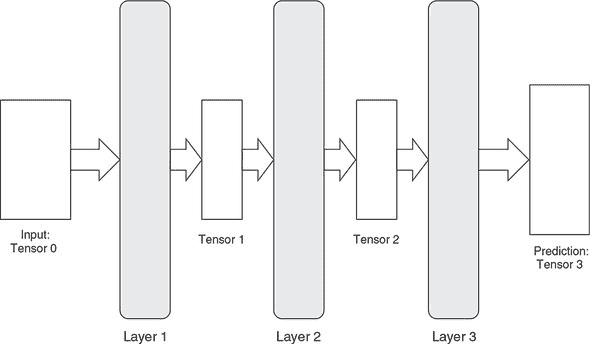
那么“流”部分呢？想象一下张量就像一种携带数据的流体。在 TensorFlow 中，它通过一个图流动——一个由相互连接的数学操作（称为节点）组成的数据结构。如图 1.7 所示，节点可以是神经网络中的连续层。每个节点将张量作为输入并产生张量作为输出。随着“张量流体”通过 TensorFlow 图“流动”，它会被转换成不同的形状和不同的值。这对应于表示的转换：也就是我们在前面的章节中描述的神经网络的要点。使用 TensorFlow，机器学习工程师可以编写各种各样的神经网络，从浅层到非常深层的网络，从用于计算机视觉的卷积网络到用于序列任务的循环神经网络（RNN）。图数据结构可以被序列化并部署到运行许多类型设备上，从大型机到手机。

图 1.7. 张量“流动”通过多个层，这在 TensorFlow 和 TensorFlow.js 中是一个常见情景。

TensorFlow 的核心设计是非常通用和灵活的：操作可以是任何明确定义的数学函数，不仅仅是神经网络层。例如，它们可以是低级数学操作，比如将两个张量相加和相乘——这种操作发生在神经网络层的内部。这使得深度学习工程师和研究人员能够为深度学习定义任意和新颖的操作。然而，对于大部分深度学习从业者来说，操作这样的低级机制比它们值得的麻烦更多。它会导致冗长和更容易出错的代码以及更长的开发周期。大多数深度学习工程师使用少数固定的层类型（例如，卷积、池化或密集层，你将在后面的章节中详细学习）。他们很少需要创建新的层类型。这就是乐高积木的类比适用的地方。使用乐高，只有少数几种积木类型。乐高建筑师不需要考虑制作一块乐高积木需要什么。这与像 Play-Doh 这样的玩具不同，它类似于 TensorFlow 的低级 API。然而，连接乐高积木的能力导致了组合成千上万种可能性和几乎无限的力量。可以用乐高或 Play-Doh 建造一个玩具房子，但除非你对房子的大小、形状、质地或材料有非常特殊的要求，否则用乐高建造房子会更容易更快。对于大多数人来说，我们建造的乐高房子将更加稳固，看起来更漂亮，而不是用 Play-Doh 建造的房子。

在 TensorFlow 的世界中，高级 API 被称为 Keras 是对应的乐高积木^([9])。Keras 提供了一组最常用的神经网络层类型，每个层都有可配置的参数。它还允许用户将层连接在一起形成神经网络。此外，Keras 还提供了以下 API：

⁹

实际上，自从引入 TensorFlow 以来，出现了许多高级 API，一些是由谷歌工程师创建的，一些是由开源社区创建的。其中最受欢迎的是 Keras、tf.Estimator、tf.contrib.slim 和 TensorLayers 等。对于本书的读者来说，与 TensorFlow.js 最相关的高级 API 无疑是 Keras，因为 TensorFlow.js 的高级 API 是基于 Keras 建模的，并且 TensorFlow.js 在模型保存和加载方面提供了双向兼容性。

• 指定神经网络的训练方式（损失函数、度量指标和优化器）

• 提供数据用于训练或评估神经网络，或使用模型进行推断

• 监控正在进行的训练过程（回调函数）

• 保存和加载模型

• 打印或绘制模型的架构

在 Keras 中，用户只需使用很少的代码即可执行完整的深度学习工作流程。低级 API 的灵活性和高级 API 的易用性使得 TensorFlow 和 Keras 在工业和学术领域的应用方面领先于其他深度学习框架（请参阅mng.bz/vlDJ上的推文）。作为不断推进的深度学习革命的一部分，不应低估它们让更广泛的人群获得深度学习的作用。在 TensorFlow 和 Keras 等框架出现之前，只有那些具有 CUDA 编程技能并且在 C++中有编写神经网络的丰富经验的人能够进行实际的深度学习。通过 TensorFlow 和 Keras，创建基于 GPU 加速的深度神经网络所需的技能和工作量大大减少。但是有一个问题：无法在 JavaScript 或直接在 Web 浏览器中运行 TensorFlow 或 Keras 模型。为了在浏览器中提供经过训练的深度学习模型，我们必须通过 HTTP 请求到后端服务器进行操作。这就是 TensorFlow.js 的用武之地。TensorFlow.js 是由 Google 的深度学习相关数据可视化和人机交互专家 Nikhil Thorat 和 Daniel Smilkov 发起的努力^([10])。正如我们所提到的，深度神经网络的高度流行的 TensorFlow Playground 演示植入了 TensorFlow.js 项目的最初种子。2017 年 9 月，发布了一个名为 deeplearn.js 的库，它具有类似于 TensorFlow 低级 API 的低级 API。 Deeplearn.js 支持 WebGL 加速的神经网络操作，使得在 Web 浏览器中以低延迟运行真实的神经网络成为可能。

¹⁰

作为一个有趣的历史注释，这些作者还在创建 TensorBoard（TensorFlow 模型的流行可视化工具）方面发挥了关键作用。

在 deeplearn.js 初始成功后，谷歌 Brain 团队的更多成员加入了该项目，并将其更名为 TensorFlow.js。JavaScript API 经过了重大改进，提高了与 TensorFlow 的 API 兼容性。此外，在底层核心之上构建了一个类似 Keras 的高级 API，使用户更容易在 JavaScript 库中定义、训练和运行深度学习模型。今天，我们对于 Keras 的力量和易用性所说的一切对于 TensorFlow.js 也完全适用。为了进一步提高互操作性，构建了转换器，使 TensorFlow.js 可以导入从 TensorFlow 和 Keras 中保存的模型，并将模型导出为它们所用的格式。自从在 2018 年春季全球 TensorFlow 开发者峰会和 Google I/O 上首次亮相以来（参见www.youtube.com/watch?v=YB-kfeNIPCE 和 www.youtube.com/watch?v=OmofOvMApTU），TensorFlow.js 快速成为了一个非常受欢迎的 JavaScript 深度学习库，在 GitHub 上类似的库中当前拥有最高的赞数和派生数。

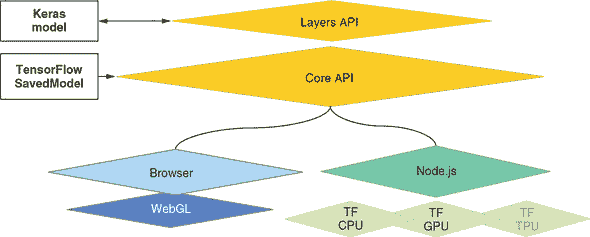
图 1.8 展示了 TensorFlow.js 的架构概述。最底层负责并行计算，用于快速数学运算。尽管大多数用户看不到此层，但它的高性能非常重要，以便在 API 的更高层级中进行模型训练和推断尽可能地快速。在浏览器中，它利用 WebGL 实现 GPU 加速（参见信息框 1.2）。在 Node.js 上，可以直接绑定到多核 CPU 并行化和 CUDA GPU 加速。这些是 TensorFlow 和 Keras 在 Python 中使用的相同的数学后端。在最低的数学层级之上建立了 Ops API，它与 TensorFlow 的低级 API 具有良好的对应性，并支持从 TensorFlow 加载 SavedModels。在最高的层级上是类似 Keras 的 Layers API。对于使用 TensorFlow.js 的大多数程序员来说，Layers API 是正确的 API 选择，也是本书的主要关注点。Layers API 还支持与 Keras 的双向模型导入/导出。

图 1.8. TensorFlow.js 的架构一览。它与 Python TensorFlow 和 Keras 的关系也显示出来。

1.3.2. 为什么选择 TensorFlow.js: 与类似库的简要比较

TensorFlow.js 并不是唯一一个用于深度学习的 JavaScript 库；也不是第一个出现的（例如，brain.js 和 ConvNetJS 的历史要长得多）。那么，为什么 TensorFlow.js 在类似的库中脱颖而出呢？第一个原因是它的全面性——TensorFlow.js 是目前唯一一个支持生产深度学习工作流中所有关键部分的库：

• 支持推断和训练

• 支持 Web 浏览器和 Node.js。

• 利用 GPU 加速（浏览器中的 WebGL 和 Node.js 中的 CUDA 核心）。

• 支持在 JavaScript 中定义神经网络模型架构。

• 支持模型的序列化和反序列化。

• 支持与 Python 深度学习框架之间的转换。

• 与 Python 深度学习框架的 API 兼容。

• 配备了内置的数据摄取支持，并提供了可视化 API。

第二个原因是生态系统。大多数 JavaScript 深度学习库定义了自己独特的 API，而 TensorFlow.js 与 TensorFlow 和 Keras 紧密集成。你有一个来自 Python TensorFlow 或 Keras 的训练模型，想在浏览器中使用它？没问题。你在浏览器中创建了一个 TensorFlow.js 模型，想将其带入 Keras 以获得更快的加速器，如 Google TPU？也可以！与非 JavaScript 框架的紧密集成不仅提升了互操作性，还使开发人员更容易在编程语言和基础设施堆栈之间迁移。例如，一旦你通过阅读本书掌握了 TensorFlow.js，如果想开始使用 Python 中的 Keras，将会非常顺利。反向旅程同样轻松：掌握 Keras 的人应该能够快速学会 TensorFlow.js（假设具备足够的 JavaScript 技能）。最后但同样重要的是，不应忽视 TensorFlow.js 的流行度和其社区的实力。TensorFlow.js 的开发人员致力于长期维护和支持该库。从 GitHub 的星星和分叉数量到外部贡献者的数量，从讨论的活跃程度到在 Stack Overflow 上的问题和答案的数量，TensorFlow.js 无愧于任何竞争库的阴影。

1.3.3. TensorFlow.js 在世界上是如何被使用的？

对于一个库的力量和流行程度，最有说服力的证明莫过于它在真实应用中的使用方式。TensorFlow.js 的几个值得注意的应用包括以下内容：

• Google 的 Project Magenta 使用 TensorFlow.js 运行 RNN 和其他类型的深度神经网络，在浏览器中生成音乐乐谱和新颖的乐器声音（magenta.tensorflow.org/demos/）。

• 丹·希夫曼（Dan Shiffman）和他在纽约大学的同事们构建了 ML5.js，这是一个易于使用的、针对浏览器的各种开箱即用的深度学习模型的高级 API，例如目标检测和图像风格转换（ml5js.org）。

• 开源开发者 Abhishek Singh 创建了一个基于浏览器的界面，将美国手语翻译成语音，以帮助不能说话或听力受损的人使用智能扬声器，如亚马逊 Echo。^([11])

  ¹¹

  Abhishek Singh，“使用你的网络摄像头和 TensorFlow.js 让 Alexa 响应手语”，Medium，2018 年 8 月 8 日，mng.bz/4eEa。

• Canvas Friends 是基于 TensorFlow.js 的类似游戏的网络应用程序，帮助用户提高其绘画和艺术技巧 (www.y8.com/games/canvas_friends)。

• MetaCar，一个在浏览器中运行的自动驾驶汽车模拟器，使用 TensorFlow.js 实现了对其模拟至关重要的强化学习算法 (www.metacar-project.com)。

• 诊所医生，一个基于 Node.js 的应用程序，用于监视服务器端程序的性能，使用 TensorFlow.js 实现了隐马尔可夫模型，并使用它来检测 CPU 使用率的峰值。^([12])

  ¹²

  Andreas Madsen，“Clinic.js Doctor Just Got More Advanced with TensorFlow.js,” Clinic.js 博客，2018 年 8 月 22 日，mng.bz/Q06w。

• 查看 TensorFlow.js 的优秀应用程序库，由开源社区构建，地址为 github.com/tensorflow/tfjs/blob/master/GALLERY.md。

1.3.4. 本书将教授和不会教授你关于 TensorFlow.js 的内容

通过学习本书中的材料，您应该能够使用 TensorFlow.js 构建如下应用程序：

• 一个能够对用户上传的图像进行分类的网站

• 深度神经网络，从浏览器连接的传感器接收图像和音频数据，并在其上执行实时机器学习任务，例如识别和迁移学习

• 客户端自然语言人工智能，如评论情感分类器，可辅助评论审核

• 一个使用千兆字节级别数据和 GPU 加速的 Node.js（后端）机器学习模型训练器

• 一个由 TensorFlow.js 提供支持的强化学习器，可以解决小规模控制和游戏问题

• 一个仪表板，用于说明经过训练的模型的内部情况和机器学习实验的结果

更重要的是，您不仅会知道如何构建和运行这些应用程序，还将了解它们的工作原理。例如，您将具有创建各种类型问题的深度学习模型所涉及的策略和约束的实际知识，以及训练和部署这些模型的步骤和技巧。

机器学习是一个广泛的领域；TensorFlow.js 是一个多才多艺的库。因此，一些应用程序完全可以使用现有的 TensorFlow.js 技术来完成，但超出了本书的范围。例如：

• 在 Node.js 环境中高性能、分布式训练深度神经网络，涉及大量数据（数量级为千兆字节）

• 非神经网络技术，例如 SVM、决策树和随机森林

• 高级深度学习应用程序，如将大型文档缩减为几个代表性句子的文本摘要引擎，从输入图像生成文本摘要的图像到文本引擎，以及增强输入图像分辨率的生成图像模型

然而，这本书将为您提供深度学习的基础知识，使您能够学习与这些高级应用相关的代码和文章。

就像任何其他技术一样，TensorFlow.js 也有其局限性。有些任务超出了它的能力范围。尽管这些限制可能在将来被推动，但了解编写时的边界是很好的：

• 在浏览器标签页中运行内存需求超出 RAM 和 WebGL 限制的深度学习模型。对于浏览器内推断，通常意味着模型总重量超过 ~100 MB。对于训练，需要更多的内存和计算资源，因此即使是较小的模型在浏览器标签页中进行训练也可能太慢了。模型训练通常还涉及比推断更大量的数据，这是评估浏览器内训练可行性时应考虑的另一个限制因素。

• 创建一个高端的强化学习器，例如能够击败人类玩家的围棋游戏。

• 使用 Node.js 进行分布式（多机器）设置来训练深度学习模型。

练习

1. 无论您是前端 JavaScript 开发人员还是 Node.js 开发人员，根据本章学到的知识，思考一下在您正在开发的系统中应用机器学习以使其更加智能的几种可能情况。可参考 表 1.1 和 1.2，以及 第 1.3.3 节。一些进一步的示例包括：

   1. 一个出售眼镜等配件的时尚网站使用网络摄像头捕获用户面部图像，并使用运行在 TensorFlow.js 上的深度神经网络检测面部标记点。然后利用检测到的标记点，在用户面部叠加太阳镜的图像，以在网页中模拟试戴体验。由于客户端推断可实现低延迟和高帧率运行，因此体验效果非常逼真。用户的数据隐私得到尊重，因为捕获的面部图像永远不会离开浏览器。

   2. 一个用 React Native（一个用于创建原生移动应用的跨平台 JavaScript 库）编写的移动体育应用程序跟踪用户的运动。使用 HTML5 API，该应用程序从手机的陀螺仪和加速度计获取实时数据。然后将数据传递给由 TensorFlow.js 驱动的模型，该模型自动检测用户当前的活动类型（例如，休息、步行、慢跑或疾跑）。

   3. 一个浏览器扩展程序会自动检测设备使用者是儿童还是成年人（通过每 5 秒一次的摄像头捕获的图像和由 TensorFlow.js 驱动的计算机视觉模型），并根据这些信息来阻止或允许访问特定网站。

   4. 基于浏览器的编程环境使用 TensorFlow.js 实现的循环神经网络来检测代码注释中的拼写错误。

   5. 基于 Node.js 的服务器端应用，使用实时信号如航空公司状态、货物类型和数量、日期/时间和交通信息等来预测每个交易的预计到达时间（ETA）。所有的训练和推理流水线均使用 TensorFlow.js 在 Node.js 中编写，从而简化了服务器堆栈。

总结

• AI 是自动化认知任务的研究。机器学习是 AI 的一个子领域，其中通过学习训练数据中的示例来自动发现执行任务（如图像分类）的规则。

• 机器学习中的一个核心问题是如何将原始数据的表示转换为更适合解决任务的表示。

• 神经网络是机器学习中的一种方法，通过数学运算的不断迭代（或层级）来转换数据表示。深度学习领域则是关注于深度神经网络，即具有多层的神经网络。

• 由于硬件的增强、标记数据的可用性和算法的进步，自 2010 年代初以来，深度学习领域取得了惊人的进展，解决了以前无法解决的问题，创造了令人兴奋的新机会。

• JavaScript 和 Web 浏览器是部署和训练深度神经网络的适宜环境。

• 本书的重点 TensorFlow.js 是一款全面、多功能和强大的 JavaScript 深度学习开源库。

第二部分：TensorFlow.js 的简介。

在覆盖了基础知识之后，在本书的这一部分，我们将以实践的方式深入探讨机器学习，使用 TensorFlow.js 作为工具。我们从第二章开始，进行一个简单的机器学习任务——回归（预测单个数字）——然后逐步向更复杂的任务发展，如第三章和第四章中的二元分类和多类分类。随着任务类型的不同，你还将看到从简单数据（一维数字数组）到更复杂数据（图像和声音）的渐进过程。我们将介绍一些方法的数学基础，比如反向传播，以及解决这些问题的代码。我们将摒弃正式的数学表达，而采用更直观的解释、图表和伪代码。

第二章：入门：TensorFlow.js 中的简单线性回归

本章内容

• 一个简单的神经网络的最小示例，用于线性回归这一简单的机器学习任务

• 张量和张量操作

• 基本神经网络优化

没有人喜欢等待，特别是当我们不知道要等多久时，等待就会变得非常烦人。任何用户体验设计师都会告诉你，如果无法隐藏延迟，那么下一个最好的办法就是给用户一个可靠的等待时间估计。估计预期延迟是一个预测问题，而 TensorFlow.js 库可以用于构建一个敏感于上下文和用户的准确下载时间预测，从而使我们能够构建清晰、可靠的体验，尊重用户的时间和注意力。

在本章中，以一个简单的下载时间预测问题作为我们的示例，我们将介绍完整机器学习模型的主要组成部分。我们将从实际角度介绍张量、建模和优化，以便你能够建立对它们是什么、如何工作以及如何适当使用它们的直觉。

深度学习内部的完全理解——这是一个专注研究者通过多年学习构建的类型——需要熟悉许多数学学科。然而，对于深度学习从业者来说，熟练掌握线性代数、微分计算和高维空间的统计学是有帮助的，但并非必需，即使要构建复杂、高性能的系统也是如此。我们在本章和整本书中的目标是根据需要介绍技术主题——尽可能使用代码，而不是数学符号。我们的目标是传达对机器的直觉理解及其目的，而不需要领域专业知识。

2.1. 示例 1：使用 TensorFlow.js 预测下载持续时间

让我们开始吧！我们将构建一个最小的神经网络，使用 TensorFlow.js 库（有时缩写为 tfjs）来预测给定下载大小的下载时间。除非你已经有 TensorFlow.js 或类似库的经验，否则你不会立即理解这个第一个示例的所有内容，但没关系。这里介绍的每个主题都将在接下来的章节中详细介绍，所以如果有些部分对你来说看起来是随意的或神奇的，不要担心！我们必须要从某个地方开始。我们将从编写一个接受文件大小作为输入并输出预测的文件下载时间的简短程序开始。

2.1.1. 项目概述：持续时间预测

当你第一次学习机器学习系统时，可能会因为各种新概念和术语而感到害怕。因此，先看一下整个工作流程是很有帮助的。这个示例的总体概述如 图 2.1 所示，并且这是我们在本书中将会反复看到的一种模式。

图 2.1. 下载时间预测系统的主要步骤概述，我们的第一个例子

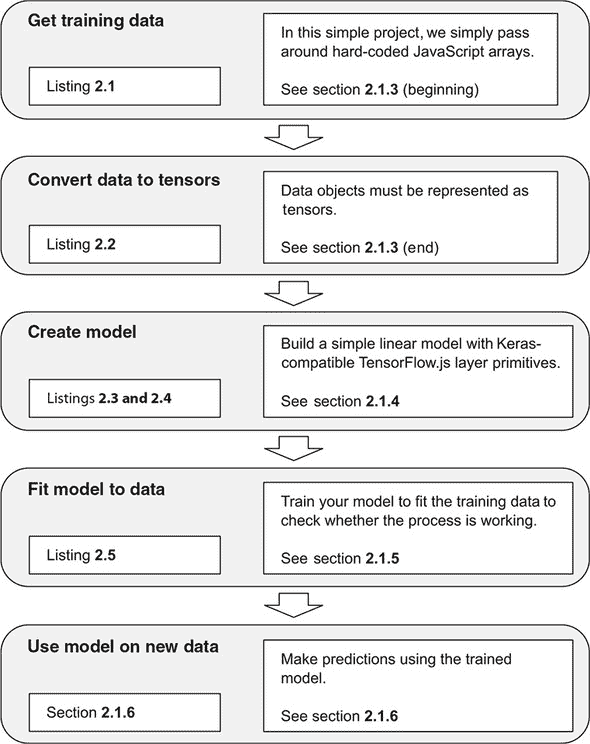
首先，我们将访问我们的训练数据。在机器学习中，数据可以从磁盘中读取，通过网络下载，生成，或者简单地硬编码。在本例中，我们采用了最后一种方法，因为它很方便，并且我们只处理了少量数据。其次，我们将把数据转换成张量，以便将其馈送到我们的模型中。下一步是创建一个模型，就像我们在第一章中看到的那样，这类似于设计一个适当的可训练函数：一个将输入数据映射到我们试图预测的事物的函数。在这种情况下，输入数据和预测目标都是数字。一旦我们的模型和数据可用，我们将训练模型，监视其报告的指标。最后，我们将使用训练好的模型对我们尚未见过的数据进行预测，并测量模型的准确性。

我们将通过每个阶段的可复制粘贴的可运行代码片段以及对理论和工具的解释来进行。

2.1.2. 有关代码清单和控制台交互的注意事项

本书中的代码将以两种格式呈现。第一种格式是代码清单，展示了您将在引用的代码仓库中找到的结构化代码。每个清单都有一个标题和一个编号。例如，清单 2.1 包含了一个非常简短的 HTML 片段，您可以将其逐字复制到一个文件中，例如 /tmp/tmp.html，在您的计算机上然后在您的 Web 浏览器中打开文件:///tmp/tmp.html，尽管它本身不会做太多事情。

第二种代码格式是控制台交互。这些更为非正式的代码块旨在传达在 JavaScript REPL（交互式解释器或 shell）^([1]) 中的示例交互，例如浏览器的 JavaScript 控制台（在 Chrome 中是 Cmd-Opt-J、Ctrl+Shift+J 或 F12，但您的浏览器/操作系统可能会有所不同）。控制台交互以前导的大于号开头，就像我们在 Chrome 或 Firefox 中看到的那样，并且它们的输出与控制台中的一样，呈现在下一行。例如，以下交互创建一个数组并打印其值。您在 JavaScript 控制台中看到的输出可能略有不同，但要点应该是相同的：

¹

Read-eval-print-loop，也称为交互式解释器或 shell。REPL 允许我们与我们的代码进行积极的交互，以查询变量和测试函数。

> let a = ['hello', 'world', 2 * 1009]
> a;
(3) ["hello", "world", 2018]

在本书中测试、运行和学习代码列表的最佳方式是克隆引用的存储库，然后与其一起玩耍。在本书的开发过程中，我们经常使用 CodePen 作为一个简单、交互式、可共享的存储库（codepen.io）。例如，列表 2.1 可供你在 codepen.io/tfjs-book/pen/VEVMbx 上玩耍。当你导航到 CodePen 时，它应该会自动运行。你应该能够看到输出打印到控制台。点击左下角的 Console 打开控制台。如果 CodePen 没有自动运行，请尝试进行一个小的、无关紧要的更改，例如在末尾添加一个空格，以启动它。

本节的列表可在此 CodePen 集合中找到：codepen.io/collection/Xzwavm/。在只有单个 JavaScript 文件的情况下，CodePen 的效果很好，但我们更大更结构化的示例保存在 GitHub 存储库中，你将在后面的示例中看到。对于这个示例，我们建议你先阅读本节，然后再玩一玩相关的 CodePen。

2.1.3. 创建和格式化数据

让我们估计一下在一台机器上下载一个文件需要多长时间，只给出其大小（以 MB 为单位）。我们首先使用一个预先创建的数据集，但如果你有动力的话，你可以创建一个类似的数据集，模拟你自己系统的网络统计信息。

列表 2.1. 硬编码训练和测试数据（来自 CodePen 2-a）

<script src='https://cdn.jsdelivr.net/npm/@tensorflow/tfjs@latest'></script>
<script>
const trainData = {
  sizeMB:  [0.080, 9.000, 0.001, 0.100, 8.000,
            5.000, 0.100, 6.000, 0.050, 0.500,
            0.002, 2.000, 0.005, 10.00, 0.010,
            7.000, 6.000, 5.000, 1.000, 1.000],
  timeSec: [0.135, 0.739, 0.067, 0.126, 0.646,
            0.435, 0.069, 0.497, 0.068, 0.116,
            0.070, 0.289, 0.076, 0.744, 0.083,
            0.560, 0.480, 0.399, 0.153, 0.149]
};
const testData = {
  sizeMB:  [5.000, 0.200, 0.001, 9.000, 0.002,
            0.020, 0.008, 4.000, 0.001, 1.000,
            0.005, 0.080, 0.800, 0.200, 0.050,
            7.000, 0.005, 0.002, 8.000, 0.008],
  timeSec: [0.425, 0.098, 0.052, 0.686, 0.066,
            0.078, 0.070, 0.375, 0.058, 0.136,
            0.052, 0.063, 0.183, 0.087, 0.066,
            0.558, 0.066, 0.068, 0.610, 0.057]
};
</script>

在上述 HTML 代码列表中，我们选择了显式包含 <script> 标签，演示了如何使用 @latest 后缀加载最新版本的 TensorFlow.js 库（在撰写本文时，此代码与 tfjs 0.13.5 兼容）。我们将在后面详细介绍不同的方式将 TensorFlow.js 导入到你的应用程序中，但在以后的过程中，我们将假定 <script> 标签已经包含在内。第一个脚本加载 TensorFlow 包并定义了符号 tf，它提供了一种引用 TensorFlow 中名称的方式。例如，tf.add() 指的是 TensorFlow 加法操作，用于将两个张量相加。在以后的过程中，我们将假设 tf 符号已经加载并在全局命名空间中可用，例如，通过之前的方式引用 TensorFlow.js 脚本。

列表 2.1 创建了两个常量，trainData和testData，分别表示下载文件所需的时间（timeSec）和文件大小（sizeMB）的 20 个样本。sizeMB中的元素与timeSec中的元素一一对应。例如，在trainData中，sizeMB的第一个元素为 0.080 MB，并且下载该文件所需时间为 0.135 秒，即 timeSec的第一个元素，依此类推。在这个示例中，我们通过在代码中直接编写数据来创建数据。这种方法在这个简单的示例中是可行的，但是当数据集的大小增长时，它很快就会变得难以管理。未来的示例将演示如何从外部存储或网络上的流数据。

回到数据上。根据图 2.2 中的绘图，我们可以看到文件大小和下载时间之间存在着可预测但并不完美的关系。现实生活中的数据是嘈杂的，但看起来我们应该能够对文件大小给出一个相当好的线性估计值。根据视觉判断，当文件大小为零时，持续时间应该约为 0.1 秒，然后每增加 1MB，持续时间大约增加 0.07 秒。请回忆起第一章中提到的，每个输入-输出对有时被称为样本。输出通常被称为目标，而输入的元素通常被称为特征。在我们的例子中，我们的 40 个样本中每个样本恰好有一个特征sizeMB和一个数值目标timeSec。

图 2.2. 下载持续时间与文件大小的测量数据。如果您对如何创建类似的绘图感兴趣，可以参考 CodePen 上的代码codepen.io/tfjs-book/pen/dgQVze。

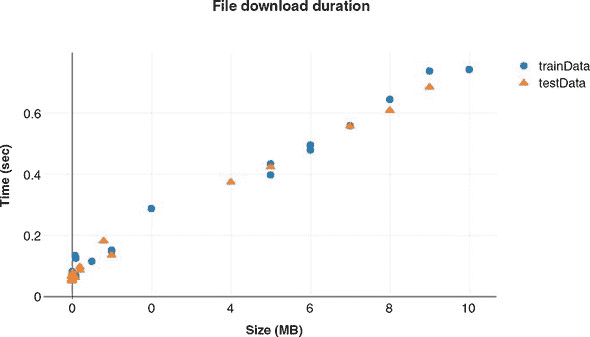
在列表 2.1 中，您可能已经注意到数据被分为两个子集，即trainData和testData。trainData是训练集，它包含了模型将会在上面进行训练的样本。testData是测试集，我们将使用它来判断模型在训练完成后的效果如何。如果我们使用完全相同的数据进行训练和评估，那就像是在已经看到答案之后进行考试。在最极端的情况下，模型可以从训练数据中理论上记住每个sizeMB对应的timeSec 值，这不是一个很好的学习算法。结果可能不是对未来性能的很好评估，因为未来输入特征的值很可能与模型进行训练时的值完全相同。

因此，工作流程如下。首先，我们将在训练数据上拟合神经网络，以便准确预测timeSec给定sizeMB。然后，我们将要求网络使用测试数据为sizeMB生成预测，并测量这些预测与timeSec的接近程度。但首先，我们必须将此数据转换为 TensorFlow.js 能够理解的格式，这将是我们对张量的第一个示例用法。代码清单 2.2 中的代码展示了在本书中你将看到的tf.*命名空间下的函数的第一个用法。在这里，我们看到了将存储在原始 JavaScript 数据结构中的数据转换为张量的方法。

尽管使用方法非常简单明了，但那些希望在这些 API 中获得更牢固基础的读者应该阅读附录 B，其中不仅涵盖了诸如tf.tensor2d()之类的张量创建函数，还涉及执行操作转换和合并张量的函数，以及常见的真实世界数据类型（如图像和视频）如何被惯例地打包成张量的模式。我们在主要文本中没有深入研究底层 API，因为这些材料有些枯燥，并且与具体的示例问题无关。

代码清单 2.2. 将数据转换为张量（来自 CodePen 2-b）

const trainTensors = {
  sizeMB: tf.tensor2d(trainData.sizeMB, [20, 1]),       ***1***
  timeSec: tf.tensor2d(trainData.timeSec, [20, 1])
};
const testTensors = {
  sizeMB: tf.tensor2d(testData.sizeMB, [20, 1]),
  timeSec: tf.tensor2d(testData.timeSec, [20, 1])
};

• 1 这里的[20, 1]是张量的“形状”。稍后会有更多解释，但在这里这个形状意味着我们希望将数字列表解释为 20 个样本，每个样本是 1 个数字。如果形状从数据数组的结构中明显，则可以省略此参数。

一般来说，所有当前的机器学习系统都使用张量作为它们的基本数据结构。张量对于该领域是至关重要的——以至于 TensorFlow 和 TensorFlow.js 都以它们命名。从第一章快速提醒：在其核心，张量是数据的容器——几乎总是数字数据。因此，它可以被认为是数字的容器。你可能已经熟悉向量和矩阵，它们分别是 1D 和 2D 张量。张量是矩阵向任意维度的泛化。张量的维数和每个维度的大小称为张量的形状。例如，一个 3 × 4 矩阵是一个形状为[3, 4]的张量。长度为 10 的向量是一个形状为[10]的 1D 张量。

在张量的上下文中，维度通常被称为轴。在 TensorFlow.js 中，张量是让组件之间通信和协同工作的常见表示，无论是在 CPU、GPU 还是其他硬件上。随着需求的出现，我们将对张量及其常见用例有更多介绍，但现在，让我们继续进行我们的预测项目。

2.1.4. 定义一个简单的模型

在深度学习的上下文中，从输入特征到目标的函数称为模型。模型函数接受特征，运行计算，并产生预测。我们正在构建的模型是一个接受文件大小作为输入并输出持续时间的函数（参见图 2.2）。在深度学习术语中，有时我们将网络用作模型的同义词。我们的第一个模型将是线性回归的实现。

回归，在机器学习的上下文中，意味着模型将输出实值，并尝试匹配训练目标；这与分类相反，后者输出来自一组选项的选择。在回归任务中，模型输出的数字越接近目标越好。如果我们的模型预测一个 1 MB 文件大约需要 0.15 秒，那就比预测一个 1 MB 文件需要约 600 秒要好（正如我们从图 2.2 中看到的）。

线性回归是一种特定类型的回归，其中输出作为输入的函数可以被表示为一条直线（或者类比为在存在多个输入特征时的高维空间中的一个平面）。模型的一个重要特性是它们是可调的。这意味着输入-输出计算可以被调整。我们利用这个特性来调整模型以更好地“拟合”数据。在线性情况下，模型的输入-输出关系总是一条直线，但我们可以调整斜率和 y 截距。

让我们构建我们的第一个网络来感受一下。

代码清单 2.3 构建线性回归模型（来自 CodePen 2-c）

const model = tf.sequential();
model.add(tf.layers.dense({inputShape: [1], units: 1}));

神经网络的核心构建模块是层，一个你可以将其视为从张量到张量的可调函数的数据处理模块。在这里，我们的网络由一个单一的密集层组成。该层对输入张量的形状有约束，由参数inputShape: [1]定义。在这里，它意味着该层期望以一维张量形式接收输入，其中恰好有一个值。来自密集层的输出始终是每个示例的一维张量，但该维度的大小由units配置参数控制。在这种情况下，我们只需要一个输出数字，因为我们试图预测的恰好是一个数字，即timeSec。

核心部分，密集层是每个输入与每个输出之间的可调整乘加。由于只有一个输入和一个输出，这个模型就是你可能从高中数学中记得的简单的y = m * x + b线性方程。密集层内部将m称为核，将b称为偏置，如图 2.3 所示。在这种情况下，我们构建了一个关于输入(sizeMB)和输出(timeSec)之间关系的线性模型：

    timeSec = kernel * sizeMB + bias

图 2.3. 我们简单线性回归模型的示意图。该模型只有一个层。模型的可调参数（或权重），即核函数和偏差，显示在密集层内部。

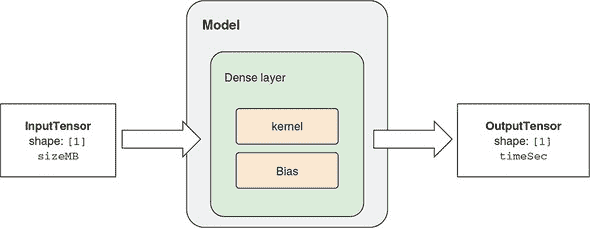
在这个方程中有四个项。就模型训练而言，其中两个是固定的：sizeMB 和 timeSec 的值由训练数据确定（见 listing 2.1）。另外两个项，即核函数和偏差，是模型的参数。它们的值在模型创建时是随机选择的。这些随机值不能很好地预测下载持续时间。为了进行良好的预测，我们必须通过允许模型从数据中学习来搜索核函数和偏差的良好值。这个搜索过程就是训练过程。

要找到核函数和偏差（统称为权重）的良好设置，我们需要两样东西：

• 一个告诉我们在给定权重设置下我们做得有多好的度量

• 一种方法来更新权重的值，以便下次我们的表现比当前更好，根据先前提到的度量

这将引导我们解决线性回归问题的下一步。为了使网络准备好进行训练，我们需要选择度量和更新方法，这对应于前面列出的两个必需项。这是 TensorFlow.js 称为模型编译步骤的一部分，它采取

• 一个损失函数—一个错误度量。这是网络在训练数据上衡量自己性能并使自己朝着正确方向前进的方式。更低的损失更好。当我们训练时，我们应该能够绘制随时间变化的损失并看到它下降。如果我们的模型训练了很长时间，而损失并没有减少，这可能意味着我们的模型没有学会拟合数据。在本书的过程中，您将学会解决此类问题。

• 一个优化器—根据数据和损失函数，网络将如何更新其权重（在本例中为核函数和偏差）的算法。

损失函数和优化器的确切目的，以及如何为它们做出良好选择，将在接下来的几章中进行彻底探讨。但现在，以下选择就足够了。

代码清单 2.4. 配置训练选项：模型编译（来自 CodePen 2-c）

model.compile({optimizer: 'sgd', loss: 'meanAbsoluteError'});

我们在模型上调用compile方法，指定'sgd'作为我们的优化器，'meanAbsoluteError'作为我们的损失。'meanAbsoluteError'表示我们的损失函数将计算我们的预测与目标的距离，取其绝对值（使它们全部为正数），然后返回这些值的平均值：

meanAbsoluteError = average( absolute(modelOutput - targets) )

例如，给定

modelOutput = [1.1, 2.2, 3.3, 3.6]
targets =     [1.0, 2.0, 3.0, 4.0]

那么，

meanAbsoluteError = average([|1.1 - 1.0|, |2.2 - 2.0|,
                             |3.3 - 3.0|, |3.6 - 4.0|])

                  = average([0.1, 0.2, 0.3, 0.4])
                  = 0.25

如果我们的模型做出非常糟糕的预测，与目标差距很大，那么meanAbsoluteError将非常大。相反，我们可能做的最好的事情是准确预测每一个，这样我们的模型输出和目标之间的差异将为零，因此损失（meanAbsoluteError）将为零。

在 list 2.4 中的sgd代表随机梯度下降，我们将在 section 2.2 中稍作描述。简而言之，这意味着我们将使用微积分来确定应该对权重进行哪些调整以减少损失；然后我们将进行这些调整并重复该过程。

我们的模型现在已经准备好适应我们的训练数据了。

2.1.5. 将模型拟合到训练数据

在 TensorFlow.js 中训练模型是通过调用模型的fit()方法来完成的。我们将模型与训练数据拟合。在这里，我们将sizeMB张量作为我们的输入，将timeSec张量作为我们期望的输出。我们还传入一个配置对象，其中包含一个epochs字段，该字段指定我们想要完全遍历我们的训练数据 10 次。在深度学习中，通过完整训练集的每次迭代称为epoch。

list 2.5. 拟合线性回归模型（来自 CodePen 2-c）

(async function() {
  await model.fit(trainTensors.sizeMB,
                  trainTensors.timeSec,
                  {epochs: 10});
})();

fit()方法通常运行时间较长，持续几秒钟或几分钟。因此，我们利用 ES2017/ES8 的async/await特性，以便在浏览器中运行时该函数不会阻塞主 UI 线程。这与 JavaScript 中其他可能运行时间较长的函数类似，例如async fetch。在这里，我们等待fit()调用完成后再继续进行，使用立即调用的异步函数表达式^([2])模式，但未来的示例将在前台线程中进行其他工作的同时在后台线程中进行训练。

²

有关立即调用的函数表达式的更多信息，请参见mng.bz/RPOZ。

一旦我们的模型完成拟合，我们就会想要看看它是否起作用。至关重要的是，我们将在训练期间未使用的数据上评估模型。在本书中，将反复出现将测试数据与训练数据分离（因此避免在测试数据上训练）的主题。这是机器学习工作流程的重要部分，你应该内化。

模型的evaluate()方法计算应用于提供的示例特征和目标的损失函数。它与fit()方法类似，因为它计算相同的损失，但evaluate()不会更新模型的权重。我们使用evaluate()来估计模型在测试数据上的质量，以便了解模型在将来应用中的表现：

> model.evaluate(testTensors.sizeMB, testTensors.timeSec).print();
Tensor
    0.31778740882873535

在这里，我们看到损失在测试数据上平均约为 0.318。考虑到，默认情况下，模型是从随机初始状态训练的，你会得到不同的值。另一种说法是，该模型的平均绝对误差（MAE）略高于 0.3 秒。这个好吗？比只估算一个常量好吗？我们可以选择一个好的常量是平均延迟。让我们看看使用这个常量会得到什么样的误差，使用 TensorFlow.js 对张量进行数学运算的支持。首先，我们将计算在训练集上计算的平均下载时间：

> const avgDelaySec = tf.mean(trainData.timeSec);
> avgDelaySec.print();
Tensor
    0.2950500249862671

接下来，让我们手动计算 meanAbsoluteError。MAE 简单地是我们的预测值与实际值之间的平均差值。我们将使用 tf.sub() 计算测试目标与我们（常量）预测之间的差值，并使用 tf.abs() 取绝对值（因为有时我们会偏低，有时偏高），然后使用 tf.mean 求平均值：

> tf.mean(tf.abs(tf.sub(testData.timeSec, 0.295))).print();
Tensor
    0.22020000219345093

请参见信息框 2.1 了解如何使用简洁的链式 API 执行相同的计算。

张量链式 API

除了标准 API 外，在 tf 命名空间下可用的张量函数之外，大多数张量函数也可以直接从张量对象本身获得，如果你喜欢，可以采用链式编程风格进行编写。下面的代码在功能上与主文中的 meanAbsoluteError 计算完全相同：

// chaining API pattern
> testData.timeSec.sub(0.295).abs().mean().print();
Tensor
    0.22020000219345093

看起来平均延迟约为 0.295 秒，总是猜测平均值比我们的网络更好地估计。这意味着我们的模型准确性甚至比一个常识性的、平凡的方法还要差！我们能做得更好吗？可能是我们训练的周期不够。请记住，在训练期间，核心和偏置的值是逐步更新的。在这种情况下，每个周期都是一步。如果模型只训练了少数周期（步骤），参数值可能没有机会接近最优值。让我们再训练几个周期，然后重新评估：

>  model.fit(trainTensors.sizeMB,
             trainTensors.timeSec,
             {epochs: 200});              ***1***

>  model.evaluate(testTensors.sizeMB, testTensors.timeSec).print();
Tensor
    0.04879039153456688

• 1 确保在执行 model.evaluate 之前等待 model.fit 返回的 promise 解析。

好多了！看起来我们之前是欠拟合，意味着我们的模型还没有足够地适应训练数据。现在我们的估计平均在 0.05 秒之内。我们比简单地猜测均值要准确四倍。在本书中，我们将提供关于如何避免欠拟合的指导，以及更隐蔽的过拟合问题的解决方法，过拟合是指模型对训练数据调整过多，导致在未见过的数据上泛化能力较差！

2.1.6 使用我们训练的模型进行预测

好的，太棒了！现在我们有了一个能够根据输入大小准确预测下载时间的模型，但我们如何使用它呢？答案是模型的 predict() 方法：

> const smallFileMB = 1;
> const bigFileMB = 100;
> const hugeFileMB = 10000;
> model.predict(tf.tensor2d([[smallFileMB], [bigFileMB],
     [hugeFileMB]])).print();
Tensor
    [[0.1373825  ],
     [7.2438402  ],
     [717.8896484]]

在这里，我们可以看到我们的模型预测一个 10,000 MB 的文件下载大约需要 718 秒。请注意，我们的训练数据中没有任何接近这个大小的例子。通常来说，对训练数据范围之外的值进行外推是非常危险的，但对于一个如此简单的问题，它可能是准确的…只要我们不遇到内存缓冲区、输入输出连接等新问题。如果我们能够收集更多在这个范围内的训练数据将会更好。

我们还看到我们需要将输入变量包装到一个适当形状的张量中。在 listing 2.3 中，我们定义inputShape为[1]，所以模型期望每个例子具有这个形状。fit()和predict()都可以一次处理多个例子。为了提供n个样本，我们将它们堆叠成一个单个输入张量，因此必须具有形状[n, 1]。如果我们忘记了，并且向模型提供了形状错误的张量，我们将得到一个形状错误的错误，如下所示：

> model.predict(tf.tensor1d([smallFileMB, bigFileMB, hugeFileMB])).print();
Uncaught Error: Error when checking : expected dense_Dense1_input to have 2
     dimension(s), but got array with shape [3]

注意此类形状不匹配的问题，因为这是一种非常常见的错误！

2.1.7. 我们第一个示例的总结

对于这个小例子来说，可以说明模型的结果。图 2.4 展示了模型在该过程中的四个点（从 10 个周期的欠拟合到收敛）。我们可以看到收敛的模型与数据非常匹配。如果你对如何绘制这种类似于图 2.4 的数据感兴趣，请访问codepen.io/tfjs-book/pen/VEVMMd上的 CodePen。

图 2.4. 训练 10、20、100 和 200 个周期后的线性模型拟合情况

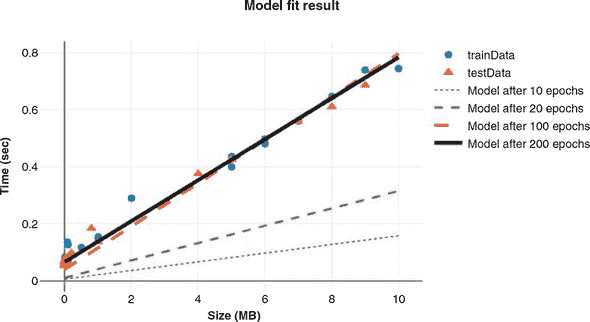
这是我们的第一个示例的结束。你刚刚看到了如何在很少的 JavaScript 代码行中构建、训练和评估一个 TensorFlow.js 模型（参见 listing 2.6）。在下一节中，我们将更深入地了解model.fit内部发生的情况。

2.6. 模型定义、训练、评估和预测

const model = tf.sequential([tf.layers.dense({inputShape: [1], units: 1})]);
model.compile({optimizer: 'sgd', loss: 'meanAbsoluteError'});
(async () => await model.fit(trainTensors.sizeMB,
                             trainTensors.timeSec,
                             {epochs: 10}))();
model.evaluate(testTensors.sizeMB, testTensors.timeSec);
model.predict(tf.tensor2d([[7.8]])).print();

2.2. Model.fit()内部: 对示例 1 中的梯度下降进行解剖

在前一节中，我们构建了一个简单的模型并拟合了一些训练数据，展示了在给定文件大小的情况下，我们可以进行相当准确的下载时间预测。它可能不是最令人印象深刻的神经网络，但它的工作方式与我们将要构建的更大、更复杂的系统完全相同。我们看到将其拟合 10 个周期并不好，但将其拟合 200 个周期产生了一个质量较高的模型^([3])。让我们更详细地了解一下模型训练时发生的确切情况。

³

注意，对于像这个简单的线性模型，存在着简单、高效、封闭形式的解。然而，这种优化方法在我们后面介绍的更复杂的模型中仍然适用。

2.2.1. 梯度下降优化背后的直觉

回想一下，我们的简单单层模型是在拟合一个线性函数f(input)，定义为

output = kernel * input + bias

这里的 kernel 和 bias 是稠密层（dense layer）中的可调参数（权重）。这些权重包含了网络从训练数据中学到的信息。

最初，这些权重被随机初始化为小的随机值（一个称为随机初始化的步骤）。当 kernel 和 bias 都是随机值时，我们当然不会指望kernel * input + bias会产生有用的结果。通过想象力，我们可以想象在不同的参数选择下，MAE 的值会如何变化。我们预期当参数近似于我们在图 2.4 中观察到的直线的斜率和截距时，损失会很低，并且当参数描述非常不同的直线时，损失会变得更糟。这个概念——损失作为所有可调参数的函数——被称为损失面。

由于这只是个小例子，我们只有两个可调参数和一个目标，所以可以将损失面绘制为 2D 等高线图，就像图 2.5 展示的那样。这个损失面呈现出一个漂亮的碗状，碗底的全局最小值代表了最佳的参数设置。然而，一个深度学习模型的损失面比这个要复杂得多。它会有多于两个维度，并且可能有很多局部最小值——也就是比附近任何点都更低但不是全局最低点的点。

图 2.5. 损失面展示了损失以及模型可调参数的等高线图。通过这个俯视图，我们可以看到选择{bias: 0.08, kernel: 0.07}（用白色 X 标记）作为低损失程度的合理选择。我们很少能有能力测试所有的参数设置来构建这样的图，但如果我们能，优化将会非常容易；只需选择对应最低损失的参数！

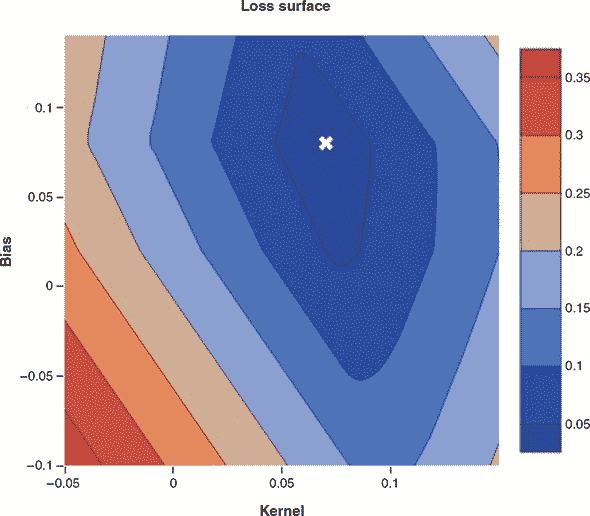
我们可以看到这个损失面的形状像个碗，最好（最低）的值在{bias: 0.08, kernel: 0.07}附近。这符合我们的数据所暗示的直线的几何形状，其中下载时间约为 0.10 秒，即使文件大小接近零。我们模型的随机初始化让我们从随机的参数设置开始，类似于地图上的随机位置，然后我们计算我们的初始损失。接下来，我们根据一个反馈信号逐渐调整参数。这个逐渐调整，也称为训练，是“机器学习”中的“学习”。这发生在一个训练循环中，如图 2.6 所示。

图 2.6. 描述训练循环，通过梯度下降更新模型

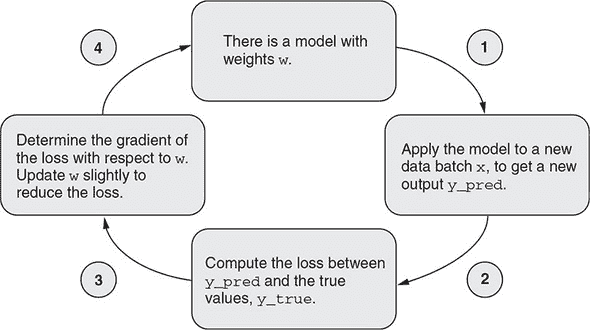
图 2.6 展示了训练循环在需要的情况下如何迭代执行这些步骤：

1. 绘制一批训练样本x和相应的目标y_true。 一批简单地将若干输入示例组合成张量。 一批中的示例数量称为批量大小。 在实际的深度学习中，通常设置为 2 的幂，例如 128 或 256。 示例被批量处理以利用 GPU 的并行处理能力，并使梯度的计算值更稳定（详情请参见第 2.2.2 节）。

2. 在x上运行网络（称为前向传递）以获得预测y_pred。

3. 计算网络在批量上的损失，这是y_true和y_pred之间不匹配的度量。 请回忆，当调用model.compile()时指定了损失函数。

4. 以稍微减少此批次上的损失的方式更新网络中的所有权重（参数）。 单个权重的详细更新由优化器管理，这是我们在model.compile()调用中指定的另一个选项。

如果您可以在每一步中降低损失，最终您将获得一个在训练数据上损失较低的网络。 网络已经“学会”将其输入映射到正确的目标。 从远处看，它可能看起来像魔术，但当简化为这些基本步骤时，事实证明它是简单的。

唯一困难的部分是步骤 4：如何确定应该增加哪些权重，应该减少哪些权重，以及数量是多少？ 我们可以简单地猜测和检查，只接受实际减少损失的更新。 对于像这样的简单问题，这样的算法可能有效，但速度会很慢。 对于更大的问题，当我们正在优化数百万个权重时，随机选择良好方向的可能性变得微乎其微。 更好的方法是利用网络中使用的所有操作都是可微分的事实，并计算损失相对于网络参数的梯度。

什么是梯度？ 不是精确定义它（需要一些微积分），我们可以直观地描述它如下：

一个方向，如果你将权重沿着那个方向微小移动，你将在所有可能的方向中最快地增加损失函数

即使这个定义并不过于技术性，仍然有很多要解释的，所以让我们试着把它分解一下：

• 首先，梯度是一个向量。 它的元素数量与权重相同。 它代表了在所有权重值选择空间中的方向。 如果您的模型的权重由两个数字组成，就像在我们的简单线性回归网络中一样，那么梯度就是一个 2D 向量。 深度学习模型通常具有数千或数百万个维度，这些模型的梯度是具有数千或数百万个元素的向量（方向）。

• 其次，梯度取决于当前的权重值。换句话说，不同的权重值会产生不同的梯度。从图 2.5 可以清楚地看出，最快下降的方向取决于您在损失曲面上的位置。在左边缘，我们必须向右走。接近底部，我们必须向上走，依此类推。

• 最后，梯度的数学定义指定了一个使损失函数增加的方向。当然，训练神经网络时，我们希望损失减少。这就是为什么我们必须沿着梯度的相反方向移动权重的原因。

比喻一下，想象一下在山脉中徒步旅行。假设我们希望前往海拔最低的地方。在这个比喻中，我们可以通过沿着东西和南北轴定义的任意方向改变我们的海拔。我们应该将第一个要点解释为，我们的海拔梯度是指在我们脚下的坡度下最陡的方向。第二个要点有点显而易见，说明最陡的方向取决于我们当前的位置。最后，如果我们希望海拔低，我们应该朝着梯度的相反方向迈步。

这个训练过程恰如其分地被命名为梯度下降。还记得在清单 2.4 中，当我们用配置optimizer: 'sgd'指定我们的模型优化器时吗？随机梯度下降中的梯度下降部分现在应该清楚了。 "随机"部分只是意味着我们在每个梯度下降步骤中从训练数据中抽取随机样本以提高效率，而不是在每个步骤中使用每个训练数据样本。随机梯度下降只是梯度下降的一个针对计算效率的修改。

现在我们有了更完整的工具来解释优化是如何工作的，以及为什么我们的下载时间估算模型的 200 个周期比 10 个周期更好。图 2.7 说明了梯度下降算法如何沿着我们的损失曲面找到一个很好地适应我们的训练数据的权重设置的路径。图 2.7 面板 A 中的等高线图显示了与之前相同的损失曲面，略微放大，并现在叠加了梯度下降算法所遵循的路径。该路径始于随机初始化——图像上的一个随机位置。由于我们事先不知道最优值，所以我们必须选择一个随机的起点！路径沿途还标出了其他几个感兴趣的点，说明了对应于欠拟合和良好拟合模型的位置。图 2.7 面板 B 显示了模型损失作为步骤的函数的图，突出显示了类似的感兴趣点。面板 C 说明了使用权重作为在 B 中突出显示的步骤的快照的模型。

图 2.7. 面板 A：使用梯度下降进行 200 次中等步长引导参数设置到局部最优解。注释突出显示了起始权重以及 20、100 和 200 个周期后的值。面板 B：损失作为周期函数的绘图，突出显示了相同点的损失。面板 C：从 sizeMB 到 timeSec 的函数，经过 10、20、100 和 200 个周期的训练得到的拟合模型所体现的，这里重复给出以便您轻松比较损失表面位置和模型输出。请访问 codepen.io/tfjs-book/pen/JmerMM 以玩耍这段代码。

我们简单的线性回归模型是本书唯一一个我们能够如此生动地可视化梯度下降过程的模型。但是当我们后面遇到更复杂的模型时，请记住梯度下降的本质仍然相同：它只是在一个复杂的、高维度表面上迭代地向下走，希望最终能够在一个损失非常低的地方停下来。

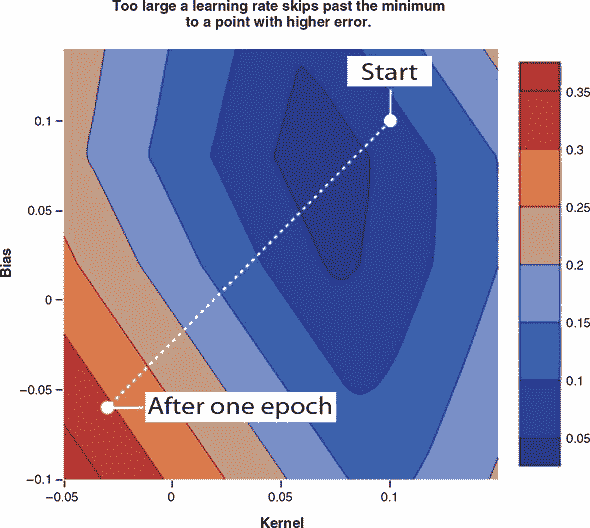
在我们的初始尝试中，我们使用了默认步长（由默认学习率确定），但是在有限数据上仅循环了 10 次时，步数不足以达到最优值；200 步足够了。一般来说，您如何知道如何设置学习率，或者如何知道训练何时完成？有一些有用的经验法则，我们将在本书的过程中介绍，但没有一条硬性规定能够永远避免麻烦。如果我们使用的学习率太小，导致步长太小，我们将无法在合理的时间内达到最优参数。相反，如果我们使用的学习率太大，因此步长太大，我们将完全跳过最小值，甚至可能比我们离开的地方的损失更高。这将导致我们模型的参数在逼近最优值时出现剧烈振荡，而不是以直接的方式快速逼近。图 2.8 示例如何当我们的梯度步长过大时会发生什么。在更极端的情况下，大的学习率会导致参数值发散并趋向无穷大，这将进一步在权重中生成 NaN（非数字）值，彻底破坏您的模型。

图 2.8. 当学习率过高时，梯度步长会过大，新参数可能比旧参数更差。这可能导致振荡行为或其他稳定性问题，导致出现无穷大或 NaN。您可以尝试将 CodePen 代码中的学习率增加到 0.5 或更高以查看此行为。

2.2.2. 反向传播：梯度下降的内部

在上一节中，我们解释了权重更新的步长如何影响梯度下降过程。但是，我们还没有讨论如何计算更新的方向。这些方向对于神经网络的学习过程是至关重要的。它们由相对于权重的梯度决定，计算这些梯度的算法称为反向传播。反向传播在 20 世纪 60 年代被发明，它是神经网络和深度学习的基础之一。在本节中，我们将使用一个简单的例子来展示反向传播的工作原理。请注意，本节是面向希望理解反向传播的读者。如果您只希望使用 TensorFlow.js 应用算法，这部分内容不是必需的，因为这些机制都被很好地隐藏在tf.Model.fit() API 下面；您可以跳过本节，继续阅读第 2.3 节。

考虑一个简单的线性模型

y’ = v * x,

其中 x 是输入特征，y’ 是预测输出，v 是在反向传播期间要更新的模型唯一的权重参数。假设我们使用平方误差作为损失函数；则我们有以下关系式，描述loss、v、x和y（实际目标值）之间的关系:

loss = square(y’ - y) = square(v * x - y)

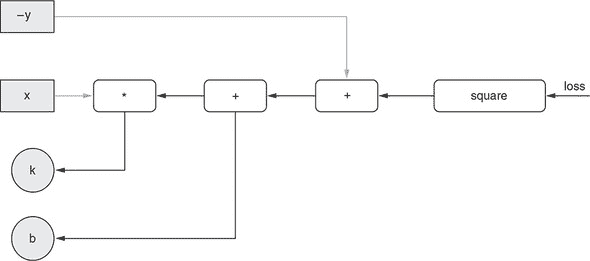
让我们假设以下具体值：两个输入变量的值为 x = 2 和 y = 5，权重值为 v = 0。损失可以计算为 25。这在图 2.9 中逐步显示。图中 A 面板中的每个灰色正方形代表一个输入变量（即x和y），每个白色方框表示一个操作。总共有三个操作。连接操作的边（以及将可调权重v与第一个操作连接的边）标记为e[1]、e[2]和e[3]。

图 2.9。通过一个只有一个可更新权重（v）的简单线性模型说明反向传播算法。A 面板：对模型的前向传递（从权重（v）和输入（x和y）计算出损失值）。B 面板：反向传递——从损失到v逐步计算损失相对于v的梯度。

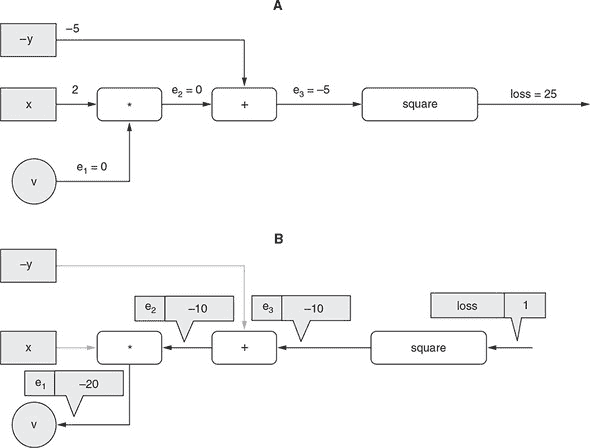
反向传播的一个重要步骤是确定以下量：

*假设其他所有内容（在这种情况下是 x 和 y）保持不变，如果 v增加一个单位，我们将获得的损失值的变化有多大？

这个量被称作相对于 v 的损失梯度。为什么我们需要这个梯度呢？因为一旦我们拥有了它，我们就可以朝着相反的方向改变 v，这样就可以得到损失值的减少。请注意，我们不需要相对于 x 或 y 的损失梯度，因为 x 和 y 不需要被更新：它们是输入数据，并且是固定的。

这个梯度是逐步计算的，从损失值开始向后退到变量v，如图 2.9 B 面所示。计算的方向是这个算法被称为“反向传播”的原因。让我们来看看具体步骤。以下每个步骤都对应着图中的一个箭头：

• 在标记为loss的边缘，我们从梯度值为 1 开始。这是一个微不足道的观点，“loss的单位增加对应着loss本身的单位增加”。

• 在标记为e[3]的边缘，我们计算损失相对于e[3]当前值的单位变化的梯度。因为中间操作是一个平方，并且从基本微积分我们知道(e[3])²相对于e[3]的导数(在一维情况下的梯度)是2 * e[3]，我们得到一个梯度值为2 * -5 = -10。值-10与之前的梯度(即 1)相乘，得到边缘e[3]上的梯度：-10。这是如果e[3]增加 1 损失将增加的量。正如你可能已经观察到的，我们用来从损失相对于一个边缘的梯度转移到相对于下一个边缘的梯度的规则是将先前的梯度与当前节点局部计算的梯度相乘。这个规则有时被称为链式法则。

• 在边缘e[2]，我们计算e[3]相对于e[2]的梯度。因为这是一个简单的add操作，梯度是 1，不管其他输入值是什么(-y)。将这个 1 与边缘e[3]上的梯度相乘，我们得到边缘e[2]上的梯度，即-10。

• 在边缘e[1]，我们计算e[2]相对于e[1]的梯度。这里的操作是x和v之间的乘法，即x * v。所以，e[2]相对于e[1]（即相对于v）的梯度是x，即 2。值 2 与边缘e[2]上的梯度相乘，得到最终的梯度：2 * -10 = -20。

到目前为止，我们已经得到了v相对于损失的梯度：它是-20。为了应用梯度下降，我们需要将这个梯度的负数与学习率相乘。假设学习率是 0.01。然后我们得到一个梯度更新为

-(-20) * 0.01 = 0.2

这是我们在训练的这一步将应用于v的更新：

v = 0 + 0.2 = 0.2

正如你所见，因为我们有x = 2和y = 5，并且要拟合的函数是y’ = v * x，v的最佳值是5/2 = 2.5。经过一步训练后，v的值从 0 变为 0.2。换句话说，权重v更接近期望值。在后续的训练步骤中，它将变得越来越接近（忽略训练数据中的任何噪声），这将基于先前描述的相同的反向传播算法。

先前的示例被故意简化，以便易于跟踪。尽管该示例捕获了反向传播的本质，但实际神经网络训练中发生的反向传播与之不同，具有以下方面：

• 通常，不是提供一个简单的训练示例（在我们的例子中是x = 2和y = 5），而是同时提供许多输入示例的批处理。用于导出梯度的损失值是所有单个示例的损失值的算术平均值。

• 被更新的变量通常有更多的元素。因此，通常涉及矩阵微积分，而不是我们刚刚做的简单的单变量导数。

• 与仅计算一个变量的梯度不同，通常涉及多个变量。图 2.10 显示了一个示例，这是一个略微更复杂的具有两个要优化变量的线性模型。除了k之外，模型还有一个偏置项：y’ = k * x + b。在这里，有两个梯度要计算，一个是为了k，另一个是为了b。反向传播的两条路径都从损失开始。它们共享一些共同的边，并形成类似树的结构。

图 2.10. 示意图显示从损失到两个可更新权重(k和b)的反向传播。

在本节中，我们对反向传播的处理是轻松和高层次的。如果您希望深入了解反向传播的数学和算法，请参考信息框 2.2 中的链接。

在这一点上，您应该对将简单模型拟合到训练数据时发生的情况有很好的理解，因此让我们将我们的小型下载时间预测问题放在一边，并使用 TensorFlow.js 来解决一些更具挑战性的问题。在下一节中，我们将构建一个模型，以同时准确预测多个输入特征的房地产价格。

有关梯度下降和反向传播的进一步阅读

优化神经网络背后的微积分绝对是有趣的，并且能够洞察到这些算法的行为；但是在基础知识之上，它绝对不是机器学习从业者的必需品，就像理解 TCP/IP 协议的复杂性对于理解如何构建现代 Web 应用程序有用但并不重要一样。我们邀请好奇的读者探索这里的优秀资源，以建立对网络中基于梯度的优化数学的更深入的理解：

• 反向传播演示滚动说明：mng.bz/2J4g

• 斯坦福 CS231 讲座 4 课程关于反向传播的课程笔记：cs231n.github.io/optimization-2/

• Andrej Karpathy 的“神经网络黑客指南:” karpathy.github.io/neuralnets/

2.3. 具有多个输入特征的线性回归

在我们的第一个示例中，我们只有一个输入特征sizeMB，用它来预测我们的目标timeSec。更常见的情况是具有多个输入特征，不确定哪些特征最具预测性，哪些只与目标松散相关，并同时使用它们，并让学习算法来处理。在本节中，我们将解决这个更复杂的问题。

到本节结束时，您将

• 了解如何构建一个模型，该模型接收并从多个输入特征中学习。

• 使用 Yarn、Git 和标准 JavaScript 项目打包结构构建和运行带有机器学习的 Web 应用程序。

• 知道如何对数据进行归一化以稳定学习过程。

• 体会如何在训练过程中使用tf.Model.fit()回调来更新 Web UI。

2.3.1. 波士顿房价数据集

波士顿房价数据集^([4])是 1970 年代末在马萨诸塞州波士顿及周边地区收集的 500 条简单的房地产记录的集合。几十年来，它一直被用作介绍性统计和机器学习问题的标准数据集。数据集中的每个独立记录都包括波士顿社区的数值测量，例如房屋的典型大小、该地区距离最近的高速公路有多远、该地区是否拥有水边物业等。表 2.1 提供了特征的精确排序列表，以及每个特征的平均值。

⁴

大卫·哈里森（David Harrison）和丹尼尔·鲁宾菲尔德（Daniel Rubinfeld），“享乐主义住房价格与对清洁空气的需求”，《环境经济与管理杂志》，第 5 卷，1978 年，第 81–102 页，mng.bz/1wvX。

表 2.1. 波士顿房屋数据集的特征

索引	特征简称	特征描述	平均值	范围（最大值-最小值）
0	CRIM	犯罪率	3.62	88.9
1	ZN	用于超过 25,000 平方英尺的住宅用地比例	11.4	100
2	INDUS	城镇中非零售业务用地（工业）比例	11.2	27.3
3	CHAS	区域是否靠近查尔斯河	0.0694	1
4	NOX	一氧化氮浓度（百万分之一）	0.555	0.49
5	RM	每个住宅的平均房间数	6.28	5.2
6	AGE	1940 年前建造的自有住房比例	68.6	97.1
7	DIS	到五个波士顿就业中心的加权距离	3.80	11.0
8	RAD	径向公路可达性指数	9.55	23.0
9	TAX	每 1 万美元的税率	408.0	524.0
10	PTRATIO	学生-教师比例	18.5	9.40
11	LSTAT	无高中学历的工作男性比例	12.7	36.2
12	MEDV	单位为 $1,000 的自有住房的中位数价值	22.5	45

在本节中，我们将构建、训练和评估一个学习系统，以估计邻域房屋价格的中位数值（MEDV），并给出邻域的所有输入特征。你可以把它想象成一个从可测量的邻域属性估计房地产价格的系统。

2.3.2. 从 GitHub 获取并运行波士顿房屋项目

由于这个问题比下载时间预测示例要复杂一些，并且有更多的组成部分，我们将首先以一个工作代码仓库的形式提供解决方案，然后引导你完成。如果你已经是 Git 源代码控制工作流和 npm/Yarn 包管理的专家，你可能只需快速浏览一下这一小节。有关基本的 JavaScript 项目结构的更多信息，请参阅 信息框 2.3。

我们将从 GitHub 上的源获取项目仓库的副本来开始。获取项目所需的 HTML、JavaScript 和配置文件。除了最简单的那些（这些都托管在 CodePen 上），本书中的所有示例都在两个 Git 仓库之一中收集，然后在仓库中分目录存放。这两个仓库分别是 tensorflow/tfjs-examples 和 tensorflow/tfjs-models，都托管在 GitHub 上。以下命令将克隆我们需要的仓库到本地，并将工作目录切换到波士顿房屋预测项目：

⁵

本书示例是开源的，托管在 github.com 和 codepen.io 上。如果你想要关于如何使用 Git 源代码控制工具的温习，GitHub 有一个很好的教程，从 help.github.com/articles/set-up-git 开始。如果你发现错误或想通过 GitHub 提交更正，请随时发送修复请求。

git clone https://github.com/tensorflow/tfjs-examples.git
cd tfjs-examples/boston-housing

本书中使用的基本 JavaScript 项目结构

本书示例中使用的标准项目结构包括三种重要类型的文件。第一种是 HTML。我们将使用的 HTML 文件将是基本的骨架，主要用于承载几个组件。通常只会有一个名为 index.html 的 HTML 文件，其中包含几个 div 标签，可能还有几个 UI 元素，以及一个 source 标签来引入 JavaScript 代码，如 index.js。

JavaScript 代码通常会模块化成多个文件，以促进良好的可读性和风格。在波士顿房屋项目中，负责更新可视元素的代码存放在 ui.js 中，而处理数据下载的代码则在 data.js 中。两者均通过 import 语句从 index.js 中引用。

我们将使用的第三种重要文件类型是元数据包 .json 文件，这是 npm 包管理器（www.npmjs.com）的要求。如果您之前没有使用过 npm 或者 Yarn，请我们建议您浏览一下 npm 的“入门”文档（docs.npmjs.com/about-npm），并且熟悉到足以构建和运行示例代码的程度。我们将使用 Yarn 作为我们的包管理器（yarnpkg.com/en/），但是如果您更喜欢使用 npm，可以将 npm 替换为 Yarn。

在存储库内，注意以下重要文件：

• index.html—根 HTML 文件，它提供 DOM 根，并调用 JavaScript 脚本

• index.js—根 JavaScript 文件，该文件加载数据，定义模型和训练循环，并指定 UI 元素

• data.js—下载和访问波士顿房价数据集所需的结构的实现

• ui.js—实现将 UI 元素与操作连接的 UI 钩子的文件；绘图配置的规范

• normalization.js—数值例程，例如从数据中减去均值

• package.json—标准的 npm 包定义，描述了构建和运行此演示所需的依赖项（例如 TensorFlow.js！）

请注意，我们不遵循将 HTML 文件和 JavaScript 文件放在特定类型的子目录中的标准做法。这种模式在更大的存储库中是最佳做法，但对于我们将在本书中使用的较小示例或您可以在 github.com/tensorflow/tfjs-examples 找到的示例，它更多地是混淆而不是澄清。

要运行此演示，请使用 Yarn：

yarn && yarn watch

这将在您的浏览器中打开一个指向 localhost 上的端口的新标签，该端口将运行示例。如果您的浏览器没有自动反应，可以在命令行中导航到输出的 URL。点击标记为“Train Linear Regressor”的按钮将触发构建线性模型并将其拟合到波士顿房价数据的过程，然后在每个周期后输出训练和测试数据集的损失的动态图表，如图 2.11 所示。

图 2.11。tfjs-examples 中的波士顿房价线性回归示例

本节的其余部分将介绍构建这个波士顿房价线性回归 Web 应用演示的重要要点。我们首先将回顾数据是如何收集和处理的，以便与 TensorFlow.js 一起使用。然后我们将重点关注模型的构建、训练和评估；最后，我们将展示如何在网页上使用模型进行实时预测。

2.3.3. 访问波士顿房价数据

在我们的第一个项目中，在清单 2.1 中，我们将数据硬编码为 JavaScript 数组，并使用tf.tensor2d函数将其转换为张量。硬编码对于小型演示来说没问题，但显然不适用于更大的应用程序。一般来说，JavaScript 开发人员会发现他们的数据位于某个 URL（可能是本地）的某种序列化格式中。例如，波士顿房屋数据以 CSV 格式公开且免费提供，可以从 Google Cloud 的以下 URL 中获取：

• storage.googleapis.com/tfjs-examples/multivariate-linear-regression/data/train-data.csv

• storage.googleapis.com/tfjs-examples/multivariate-linear-regression/data/train-target.csv

• storage.googleapis.com/tfjs-examples/multivariate-linear-regression/data/test-data.csv

• storage.googleapis.com/tfjs-examples/multivariate-linear-regression/data/test-target.csv

数据已经通过将样本随机分配到训练和测试部分而进行了预拆分。大约有三分之二的样本在训练拆分中，剩下的三分之一用于独立评估经过训练的模型。此外，对于每个拆分，目标特征已经与其他特征分开成为 CSV 文件，导致了表 2.2 中列出的四个文件名。

表 2.2. 波士顿房屋数据集的拆分和内容的文件名

		特征（12 个数字）	目标（1 个数字）
训练-测试拆分	训练	train-data.csv	train-target.csv
	测试	test-data.csv	test-target.csv

为了将这些数据引入我们的应用程序，我们需要能够下载这些数据并将其转换为适当类型和形状的张量。波士顿房屋项目在 data.js 中定义了一个名为BostonHousingDataset的类，用于此目的。该类抽象了数据集流操作，提供了一个 API 来检索原始数据作为数字矩阵。在内部，该类使用了公共开源 Papa Parse 库（www.papaparse.com）来流式传输和解析远程 CSV 文件。一旦文件已加载和解析，库就会返回一个数字数组的数组。然后，使用与第一个示例中相同的 API 将其转换为张量，如下清单所示，这是index.js中的一个略微简化的示例，重点放在相关部分上。

清单 2.7. 在 index.js 中将波士顿房屋数据转换为张量

// Initialize a BostonHousingDataset object defined in data.js.
const bostonData = new BostonHousingDataset();
const tensors = {};

// Convert the loaded csv data, of type number[][] into 2d tensors.
export const arraysToTensors = () => {
  tensors.rawTrainFeatures = tf.tensor2d(bostonData.trainFeatures);
  tensors.trainTarget = tf.tensor2d(bostonData.trainTarget);
  tensors.rawTestFeatures = tf.tensor2d(bostonData.testFeatures);
  tensors.testTarget = tf.tensor2d(bostonData.testTarget);
}

// Trigger the data to load asynchronously once the page has loaded.
let tensors;
document.addEventListener('DOMContentLoaded', async () => {
  await bostonData.loadData();
  arraysToTensors();
}, false);

2.3.4. 精确定义波士顿房屋问题

现在我们可以以我们想要的形式访问我们的数据，现在是时候更准确地澄清我们的任务了。我们说我们想要从其他字段预测 MEDV，但是我们将如何确定我们的工作是否做得好呢？我们如何区分一个好模型和一个更好的模型呢？

我们在第一个例子中使用的度量标准meanAbsoluteError将所有错误都视为平等。如果只有 10 个样本，并且我们对所有 10 个样本进行预测，并且我们在其中的第 10 个样本上完全正确，但在其他 9 个样本上偏差为 30，则meanAbsoluteError将为 3（因为 30/10 为 3）。如果我们的预测对每个样本都偏差为 3，那么meanAbsoluteError仍然为 3。这个“错误的平等性”原则可能似乎是唯一显然正确的选择，但是选择除meanAbsoluteError之外的损失度量有很好的理由。

另一种选择是将大错误的权重赋予小错误。我们可以不是取绝对误差的平均值，而是取平方误差的平均值。

在进行有关这 10 个样本的案例研究时，这种均方误差（MSE）方法看到了在每个示例上偏差为 3 时（10 × 3² = 90）比在一个示例上偏差为 30 时（1 × 30² = 900）较低的损失。由于对大错误的敏感性，平方误差比绝对误差更敏感于样本异常值。将模型拟合以最小化 MSE 的优化器将更喜欢系统地犯小错误的模型，而不是偶尔给出非常糟糕估计的模型。显然，这两种错误度量都会更喜欢根本没有错误的模型！但是，如果您的应用可能对非常不正确的异常值敏感，那么 MSE 可能比 MAE 更好。选择 MSE 或 MAE 的其他技术原因，但它们在此时并不重要。在本例中，我们将使用 MSE 来增加变化，但 MAE 也足够。

在我们继续之前，我们应该找到损失的基准估计。如果我们不知道从一个非常简单的估计中得出的误差，那么我们就没有能力从一个更复杂的模型中评估它。我们将使用平均房地产价格作为我们的“最佳天真猜测”，并计算总是猜测该值时的误差。

列表 2.8. 计算猜测平均价格的基线损失

export const computeBaseline = () => {
  const avgPrice = tf.mean(tensors.trainTarget);             ***1***
  console.log(`Average price: ${avgPrice.dataSync()[0]}`);

  const baseline =
      tf.mean(tf.pow(tf.sub(
          tensors.testTarget, avgPrice), 2));                ***2***

  console.log(
      `Baseline loss: ${baseline.dataSync()[0]}`);           ***3***
};

• 1 计算平均价格

• 2 计算测试数据上的平均平方误差。sub()、pow 和 mean() 调用是计算平均平方误差的步骤。

• 3 打印出损失值

因为 TensorFlow.js 通过在 GPU 上进行调度来优化其计算，所以张量可能并不总是可供 CPU 访问。在列表 2.8 中对dataSync的调用告诉 TensorFlow.js 完成张量的计算，并将值从 GPU 拉到 CPU 中，以便可以打印出来或以其他方式与非 TensorFlow 操作共享。

当执行时，列表 2.8 中的代码将在控制台中产生以下输出：

Average price: 22.768770217895508
Baseline loss: 85.58282470703125

这告诉我们，天真的误差率大约为 85.58。如果我们构建一个总是输出 22.77 的模型，该模型在测试数据上将达到 85.58 的 MSE。再次注意，我们在训练数据上计算指标，并在测试数据上评估它，以避免不公平的偏见。

平均平方误差为 85.58，所以我们应该取平方根得到平均误差。85.58 的平方根大约是 9.25。因此，我们可以说我们期望我们的（常量）估计平均偏离（上下）约 9.25。根据表 2.1 的数值，以千美元为单位，估计一个常量意味着我们会偏离约 9,250 美元。如果这对我们的应用程序足够好，我们可以停止！明智的机器学习从业者知道何时避免不必要的复杂性。让我们假设我们的价格估计应用程序需要比这更接近。我们将通过拟合我们的数据来查看是否可以获得比 85.58 更好的 MSE 的线性模型。

2.3.5。稍微偏离数据标准化

查看波士顿房屋的特征，我们会看到各种值。NOX 的范围在 0.4 到 0.9 之间，而 TAX 则从 180 到 711。为了拟合线性回归，优化器将尝试找到每个特征的权重，使特征的累加乘以权重大约等于房屋价格。请记住，为了找到这些权值，优化器正在寻找，遵循权重空间中的梯度。如果某些特征与其他特征的比例相差很大，那么某些权重将比其他权重敏感得多。向一个方向的一个非常小的移动将比另一个方向的一个非常大的移动更改输出。这可能导致不稳定，并使得难以拟合模型。

为了对抗这一点，我们将首先标准化我们的数据。这意味着我们将缩放我们的特征，使它们的平均值为零，标准差为单位。这种标准化方法很常见，也可以被称为标准转换或z-score 标准化。做这种操作的算法很简单——我们首先计算每个特征的平均值，并从原始值中减去，使得该特征的平均值为零。然后我们计算特征的标准差与减去的平均值，并进行除法。在伪代码中，

normalizedFeature = (feature - mean(feature)) / std(feature)

例如，当特征是[10, 20, 30, 40]时，标准化后的版本大约是[-1.3, -0.4, 0.4, 1.3]，很明显的平均值为零；肉眼看，标准差大约为一。在波士顿房屋的例子中，标准化代码被分解到一个单独的文件中，normalization.js，其内容在列表 2.9 中。在这里，我们看到两个函数，一个用于计算所提供的二维张量的平均值和标准差，另一个用于在提供预先计算的平均值和标准差的情况下标准化张量。

列表 2.9。数据规范化：零均值，单位标准差

/**
 * Calculates the mean and standard deviation of each column of an array.
 *
 * @param {Tensor2d} data Dataset from which to calculate the mean and
 *                        std of each column independently.
 *
 * @returns {Object} Contains the mean and std of each vector
 *                   column as 1d tensors.
 */
export function determineMeanAndStddev(data) {
  const dataMean = data.mean(0);
  const diffFromMean = data.sub(dataMean);
  const squaredDiffFromMean = diffFromMean.square();
  const variance = squaredDiffFromMean.mean(0);
  const std = variance.sqrt();
  return {mean, std};
}
/**
 * Given expected mean and standard deviation, normalizes a dataset by
 * subtracting the mean and dividing by the standard deviation.
 *
 * @param {Tensor2d} data: Data to normalize.
 *    Shape: [numSamples, numFeatures].
 * @param {Tensor1d} mean: Expected mean of the data. Shape [numFeatures].
 * @param {Tensor1d} std: Expected std of the data. Shape [numFeatures]
 *
 * @returns {Tensor2d}: Tensor the same shape as data, but each column
 * normalized to have zero mean and unit standard deviation.
 */
export function normalizeTensor(data, dataMean, dataStd) {
  return data.sub(dataMean).div(dataStd);
}

让我们稍微深入一下这些函数。函数determineMeanAndStddev将data作为输入，这是一个秩 2 张量。按照惯例，第一个维度是样本维度：每个索引对应一个独立，唯一的样本。第二个维度是特征维度：其 12 个元素对应于 12 个输入特征（如 CRIM，ZN，INDUS 等）。由于我们要独立计算每个特征的平均值，因此调用

const dataMean = data.mean(0);

这个调用中的0表示平均值是在第 0 维度（第一维度）上计算的。记得data是一个二维张量，因此有两个维度（或轴）。第一个轴，即“批处理”轴，是样本维度。当我们沿着该轴从第一个到第二个到第三个元素移动时，我们引用不同的样本，或者在我们的情况下，不同的房地产部分。第二个维度是特征维度。当我们在该维度的第一个元素移动到第二个元素时，我们引用不同的特征，例如 CRIM，ZN 和 INDUS，来自表 2.1。当我们沿轴 0 取平均值时，我们正在沿样本方向取平均值。结果是具有仅保留特征轴的秩 1 张量。我们拥有每个特征的平均值。如果我们改为沿轴 1 取平均值，我们仍会得到一个秩 1 张量，但剩余轴将是样本维度。这些值将对应于每个房地产部分的平均值，这在我们的应用程序中没有意义。在使用轴进行计算时，请注意在正确方向上进行计算，因为这是常见的错误来源。

果然，如果我们在这里设置一个断点^([6])，我们可以使用 JavaScript 控制台来探索计算出的平均值，我们看到的平均值非常接近我们为整个数据集计算的值。这意味着我们的训练样本是代表性的：

⁶

在 Chrome 中设置断点的说明在这里：mng.bz/rPQJ。如果您需要 Firefox，Edge 或其他浏览器中断点设置说明，您可以使用您喜欢的搜索引擎搜索“如何设置断点”。

> dataMean.shape
[12]
> dataMean.print();
     [3.3603415, 10.6891899, 11.2934837, 0.0600601, 0.5571442, 6.2656188,
     68.2264328, 3.7099338, 9.6336336, 409.2792969, 18.4480476, 12.5154343]

在下一行中，我们通过使用tf.sub从我们的数据中减去平均值，从而获得数据的中心版本：

const diffFromMean = data.sub(dataMean);

如果您没有 100％的注意力，这一行可能会隐藏一个迷人的小魔术。您看，data是一个形状为[333,12]的秩 2 张量，而dataMean是一个形状为[12]的秩 1 张量。通常情况下，不可能减去具有不同形状的两个张量。但是，在这种情况下，TensorFlow 使用广播将第二个张量的形状扩展为在效果上重复它 333 次，而不使其清楚地拼写出来。这种易用性使操作变得更加简单，但是有时广播兼容的形状规则可能有点令人困惑。如果您对广播的细节感兴趣，请直接阅读信息框 2.4。

determineMeanAndStddev函数的下几行没有新的惊喜：tf.square()将每个元素乘以自身，而tf.sqrt()获取元素的平方根。每种方法的详细 API 在 TensorFlow.js API 参考文档中都有记录，js.tensorflow.org/api/latest/。该文档页面还具有实时的可编辑小部件，可以让您探索如何将函数与自己的参数值一起使用，如图 2.12 所示。

图 2.12。js.tensorflow.org的 TensorFlow.js API 文档允许您在文档内直接探索和交互使用 TensorFlow API。这使得理解函数用途和棘手的边界案例变得简单而快速。

在这个例子中，我们编写了代码以优先考虑阐述的清晰度，但是determineMeanAndStddev函数可以更简洁地表达：

const std = data.sub(data.mean(0)).square().mean().sqrt();

你应该能够看到，TensorFlow 允许我们在不使用很多样板代码的情况下表达相当多的数字计算。

广播

考虑一个张量运算，如C = tf.someOperation（A，B），其中A和B是张量。如果可能且没有歧义，较小的张量将被扩展到与较大的张量匹配的形状。广播包括两个步骤：

1. 小张量添加轴（称为广播轴）以匹配大张量的秩。

2. 较小的张量将沿着这些新轴重复以匹配大张量的完整形状。

在实现方面，实际上没有创建新的张量，因为那将非常低效。重复操作完全是虚拟的，在算法级别而不是在内存级别上发生。但是思考较小张量沿着新轴重复是有帮助的。

通过广播，如果一个张量的形状为(a, b, ..., n, n + 1, ... m)，另一个张量的形状为(n, n + 1, ... , m)，通常可以对两个张量进行逐元素操作。广播将自动发生在轴a到n - 1。例如，以下示例通过广播在不同形状的两个随机张量上应用逐元素maximum操作：

x = tf.randomUniform([64, 3, 11, 9]);    ***1***
y = tf.randomUniform([11, 9]);           ***2***
z = tf.maximum(x, y);                    ***3***

• 1 x 是一个形状为 [64, 3, 11, 9] 的随机张量。

• 2 y 是一个形状为 [11, 9] 的随机张量。

• 3 输出 z 的形状与 x 相同，为 [64, 3, 11, 9]。

2.3.6. 波士顿房屋数据的线性回归

我们的数据已经归一化，并且我们已经完成了对数据的尽职调查工作，计算出了一个合理的基线——下一步是构建和拟合一个模型，看看我们是否能超越基线。在 listing 2.10 中，我们定义了一个线性回归模型，就像我们在 section 2.1 中所做的那样（来自 index.js）。代码非常相似；我们从下载时间预测模型看到的唯一区别在于 inputShape 配置，它现在接受长度为 12 的向量，而不是 1。单个密集层仍然具有 units: 1，表示输出为一个数字。

Listing 2.10. 为波士顿房屋定义线性回归模型

export const linearRegressionModel = () => {
  const model = tf.sequential();
  model.add(tf.layers.dense(
      {inputShape: [bostonData.numFeatures], units: 1}));
  return model;
};

在我们的模型被定义之后，但在我们开始训练之前，我们必须通过调用model.compile来指定损失和优化器。在 listing 2.11 中，我们看到指定了'meanSquaredError'损失，并且优化器使用了自定义的学习率。在我们之前的示例中，优化器参数被设置为字符串'sgd'，但现在是tf.train.sgd(LEARNING_RATE)。这个工厂函数将返回一个代表随机梯度下降优化算法的对象，但是参数化了我们自定义的学习率。这是 TensorFlow.js 中的一个常见模式，借鉴自 Keras，并且你将看到它被用于许多可配置选项。对于标准、已知的默认参数，字符串标记值可以替代所需的对象类型，TensorFlow.js 将使用良好的默认参数替换所需对象的字符串。在这种情况下，'sgd'将被替换为tf.train.sgd(0.01)。当需要额外的定制时，用户可以通过工厂函数构建对象并提供所需的定制值。这允许代码在大多数情况下简洁，但允许高级用户在需要时覆盖默认行为。

Listing 2.11. 为波士顿房屋模型编译（来自 index.js）

const LEARNING_RATE = 0.01;
model.compile({
    optimizer: tf.train.sgd(LEARNING_RATE),
    loss: 'meanSquaredError'});

现在我们可以使用训练数据集训练我们的模型。在列表 2.12 到 2.14 中，我们将使用model.fit()调用的一些附加功能，但本质上它与图 2.6 中的情况相同。在每一步中，它从特征（tensors.trainFeatures）和目标（tensors.trainTarget）中选择一定数量的新样本，计算损失，然后更新内部权重以减少该损失。该过程将在训练数据上进行NUM_EPOCHS次完整的遍历，并且在每一步中将选择BATCH_SIZE个样本。

图 2.12. 在波士顿房屋数据上训练我们的模型

await model.fit(tensors.trainFeatures, tensors.trainTarget, {
  batchSize: BATCH_SIZE
  epochs: NUM_EPOCHS,
});

在波士顿房价 Web 应用程序中，我们展示了一个图表，显示模型训练时的训练损失。这需要使用model.fit()回调功能来更新用户界面。model.fit()回调 API 允许用户提供回调函数，在特定事件发生时执行。截至版本 0.12.0，回调触发器的完整列表包括onTrainBegin、onTrainEnd、onEpochBegin、onEpochEnd、onBatchBegin和onBatchEnd。

图 2.13. model.fit()中的回调函数

let trainLoss;
await model.fit(tensors.trainFeatures, tensors.trainTarget, {
  batchSize: BATCH_SIZE,
  epochs: NUM_EPOCHS,
  callbacks: {
    onEpochEnd: async (epoch, logs) => {
      await ui.updateStatus(
         `Epoch ${epoch + 1} of ${NUM_EPOCHS} completed.`);
      trainLoss = logs.loss;
      await ui.plotData(epoch, trainLoss);
    }
  }
});

这里介绍的最后一个新的自定义是利用验证数据。验证是一个值得解释的机器学习概念。在早期的下载时间示例中，我们将训练数据与测试数据分开，因为我们想要一个对模型在新的、未见过的数据上的性能进行无偏估计。通常情况下，还有一个称为验证数据的拆分。验证数据与训练数据和测试数据都是分开的。验证数据用于什么？机器学习工程师将在验证数据上看到结果，并使用该结果来更改模型的某些配置¹，以提高验证数据上的准确性。这都很好。然而，如果这个周期足够多次，那么我们实际上是在验证数据上进行调优。如果我们使用相同的验证数据来评估模型的最终准确性，那么最终评估的结果将不再具有泛化性，因为模型已经看到了数据，并且评估结果不能保证反映模型在未来未见数据上的表现。这就是将验证数据与测试数据分开的目的。这个想法是我们将在训练数据上拟合我们的模型，并根据验证数据上的评估来调整其超参数。当我们完成并满意整个过程时，我们将在测试数据上仅对模型进行一次评估，以获得最终的、可推广的性能估计。

⁷

这些配置的示例包括模型中的层数、层的大小、训练过程中使用的优化器类型和学习率等。它们被称为模型的超参数，我们将在下一章的 section 3.1.2 中更详细地介绍。

让我们总结一下训练、验证和测试集在 TensorFlow.js 中的作用以及如何使用它们。并非所有项目都会使用这三种类型的数据。经常，快速探索或研究项目只会使用训练和验证数据，而不会保留一组“纯”数据用于测试。虽然不太严谨，但这有时是对有限资源的最佳利用：

• 训练数据—用于梯度下降优化模型权重

  • 在 TensorFlow.js 中的用法：通常，使用主要参数（x和y）对Model.fit(x, y, config)进行调用来使用训练数据。

• 验证数据—用于选择模型结构和超参数

  • 在 TensorFlow.js 中的用法：Model.fit() 有两种指定验证数据的方式，都作为config参数的一部分。如果您作为用户具有明确的用于验证的数据，则可以指定为config.validationData。相反，如果您希望框架拆分一些训练数据并将其用作验证数据，则可以在config.validationSplit中指定要使用的比例。框架将确保不使用验证数据来训练模型，因此不会有重叠。

• 测试数据—用于对模型性能进行最终、无偏的估计

  • 在 TensorFlow.js 中的用法：通过将其作为x和y参数传递给Model.evaluate(x, y, config)，可以向系统公开评估数据。

在 列表 2.14 中，验证损失与训练损失一起计算。validationSplit: 0.2字段指示model.fit()机制选择最后 20%的训练数据用作验证数据。这些数据将不用于训练（不影响梯度下降）。

列表 2.14. 在 model.fit() 中包含验证数据

let trainLoss;
let valLoss;
await model.fit(tensors.trainFeatures, tensors.trainTarget, {
  batchSize: BATCH_SIZE,
  epochs: NUM_EPOCHS,
  validationSplit: 0.2,
  callbacks: {
    onEpochEnd: async (epoch, logs) => {
      await ui.updateStatus(
          `Epoch ${epoch + 1} of ${NUM_EPOCHS} completed.`);
      trainLoss = logs.loss;
      valLoss = logs.val_loss;
      await ui.plotData(epoch, trainLoss, valLoss);
    }
  }
});

在浏览器上将此模型训练到 200 个周期大约需要 11 秒。我们现在可以对我们的测试集上评估模型，以查看它是否比基准更好。下一个列表显示了如何使用model.evaluate()来收集模型在我们保留的测试数据上的性能，然后调用我们的自定义 UI 例程来更新视图。

列表 2.15. 在测试数据上评估我们的模型并更新 UI（来自 index.js）

await ui.updateStatus('Running on test data...');
const result = model.evaluate(
    tensors.testFeatures, tensors.testTarget, {batchSize: BATCH_SIZE});
const testLoss = result.dataSync()[0];
await ui.updateStatus(
    `Final train-set loss: ${trainLoss.toFixed(4)}\n` +
    `Final validation-set loss: ${valLoss.toFixed(4)}\n` +
    `Test-set loss: ${testLoss.toFixed(4)}`);

在这里，model.evaluate()返回一个标量（记住，一个秩为 0 的张量），其中包含对测试集计算得出的损失。

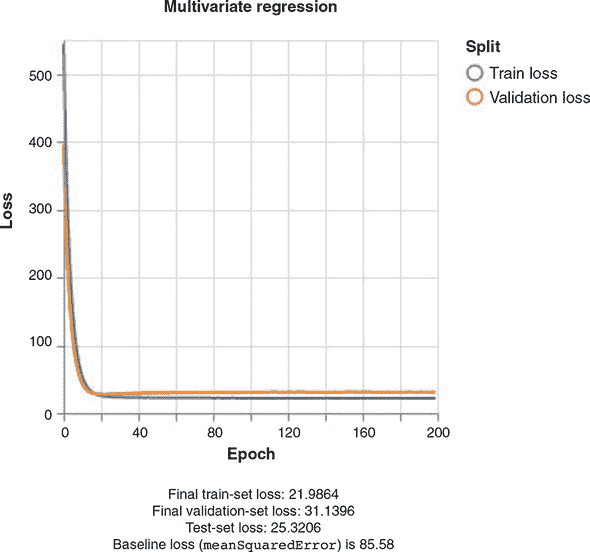
由于梯度下降中涉及随机性，您可能会得到不同的结果，但以下结果是典型的：

• 最终的训练集损失: 21.9864

• 最终的验证集损失: 31.1396

• 测试集损失: 25.3206

• 基准损失: 85.58

我们从中看到，我们的最终无偏估计错误约为 25.3，远远好于我们的天真基线 85.6。回想一下，我们的错误是使用meanSquaredError计算的。取平方根，我们看到基线估计通常偏离了 9.2 以上，而线性模型仅偏离了约 5.0。相当大的改进！如果我们是世界上唯一拥有这些信息的人，我们可能是 1978 年波士顿最好的房地产投资者！除非，以某种方式，有人能够建立一个更准确的估算……

如果你让好奇心超过了自己，并点击了训练神经网络回归器，你已经知道可以得到更好的估计。在下一章中，我们将介绍非线性深度模型，展示这样的成就是如何可能的。

2.4. 如何解释你的模型

现在我们已经训练了我们的模型，并且它能够做出合理的预测，自然而然地想知道它学到了什么。有没有办法窥视模型，看看它是如何理解数据的？当模型为输入预测了一个特定的价格时，你能否找到一个可以理解的解释来解释它为什么得出这个值？对于大型深度网络的一般情况，模型理解——也称为模型可解释性——仍然是一个活跃的研究领域，在学术会议上填满了许多海报和演讲。但对于这个简单的线性回归模型来说，情况相当简单。

到本节结束时，你将

• 能够从模型中提取学到的权重。

• 能够解释这些权重，并将它们与你对权重应该是什么的直觉进行权衡。

2.4.1. 从学到的权重中提取含义

我们在 section 2.3 中构建的简单线性模型包含了 13 个学到的参数，包含在一个核和一个偏差中，就像我们在 section 2.1.3 中的第一个线性模型一样：

output = kernel · features + bias

核和偏差的值都是在拟合模型时学到的。与 section 2.1.3 中学到的标量线性函数相比，这里，特征和核都是向量，而“·”符号表示内积，是标量乘以向量的一般化。内积，也称为点积，简单地是匹配元素的乘积的和。清单 2.16 中的伪代码更精确地定义了内积。

我们应该从中得出结论，特征的元素与核的元素之间存在关系。对于每个单独的特征元素，例如表 table 2.1 中列出的“犯罪率”和“一氧化氮浓度”，核中都有一个关联的学到的数字。每个值告诉我们一些关于模型对这个特征学到了什么以及这个特征如何影响输出的信息。

清单 2.16. 内积伪代码

function innerProduct(a, b) {
    output = 0;
    for (let i = 0 ; i < a.length ; i++) {
        output += a[i] * b[i];
    }
    return output;
}

例如，如果模型学到了kernel[i]是正的，那么这意味着如果feature[i]的值较大，则输出将更大。反之，如果模型学到了kernel[j]是负的，那么较大的feature[j]值会减少预测的输出。学到的值在大小上非常小意味着模型认为相关特征对预测的影响很小，而具有大幅度的学习值则表明模型对该特征的重视程度很高，并且特征值的微小变化将对预测产生相对较大的影响。^([8])

⁸

注意，只有在特征已经被归一化的情况下，才能以这种方式比较其大小，就像我们为波士顿房屋数据集所做的那样。

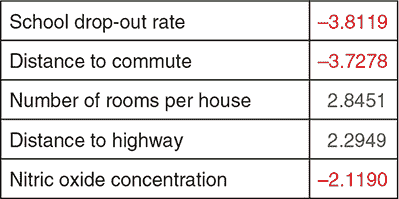
为了具体化，根据绝对值排名，前五个特征值被打印在图 2.13 中，以显示波士顿房屋示例的输出区域中的一个运行。由于初始化的随机性，后续运行可能会学到不同的值。我们可以看到对于我们期望对房地产价格产生负面影响的特征，例如当地居民辍学率和房地产距离理想工作地点的距离，其值是负的。对于我们期望与价格直接相关的特征，例如房产中的房间数量，学到的权重是正的。

图 2.13。根据绝对值排名，这是在波士顿房屋预测问题的线性模型的一个运行中学到的前五个权重。注意对那些你期望对房价产生负面影响的特征的负值。

2.4.2。从模型中提取内部权重

学到的模型的模块化结构使得提取相关权重变得容易；我们可以直接访问它们，但是有几个需要通过的 API 级别以获取原始值。重要的是要记住，由于值可能在 GPU 上，而设备间通信是昂贵的，请求这些值是异步的。列表 2.17 中的粗体代码是对 model.fit 回调的补充，扩展了 列表 2.14 以在每个 epoch 后说明学到的权重。我们将逐步讲解 API 调用。

给定模型，我们首先希望访问正确的层。这很容易，因为这个模型中只有一个层，所以我们可以在 model.layers[0] 处获得它的句柄。现在我们有了层，我们可以使用 getWeights() 访问内部权重，它返回一个权重数组。对于密集层的情况，这将始终包含两个权重，即核和偏置，顺序是这样的。因此，我们可以在以下位置访问正确的张量：

> model.layers[0].getWeights()[0]

现在我们有了正确的张量，我们可以通过调用其 data() 方法来访问其内容。由于 GPU ↔ CPU 通信的异步性质，data() 是异步的，并返回张量值的一个承诺，而不是实际值。在 2.17 节 中，通过将承诺的 then() 方法传递给回调函数，将张量值绑定到名为 kernelAsArr 的变量上。如果取消注释 console.log() 语句，则像下面这样的语句，列出内核值，将在每个纪元结束时记录到控制台：

> Float32Array(12) [-0.44015952944755554, 0.8829045295715332,
     0.11802537739276886, 0.9555914402008057, -1.6466193199157715,
     3.386948347091675, -0.36070501804351807, -3.0381457805633545,
     1.4347705841064453, -1.3844640254974365, -1.4223048686981201,
     -3.795234441757202]

2.17. 访问内部模型值

let trainLoss;
let valLoss;
await model.fit(tensors.trainFeatures, tensors.trainTarget, {
  batchSize: BATCH_SIZE,
  epochs: NUM_EPOCHS,
  validationSplit: 0.2,
  callbacks: {
    onEpochEnd: async (epoch, logs) => {
      await ui.updateStatus(
          `Epoch ${epoch + 1} of ${NUM_EPOCHS} completed.`);
      trainLoss = logs.loss;
        valLoss = logs.val_loss;
      await ui.plotData(epoch, trainLoss, valLoss);
      model.layers[0].getWeights()[0].data().then(kernelAsArr => {
        // console.log(kernelAsArr);
        const weightsList = describeKerenelElements(kernelAsArr);
        ui.updateWeightDescription(weightsList);
      });
    }
  }
});

2.4.3. 解释性的注意事项

在 图 2.13 中的权重讲述了一个故事。作为人类读者，你可能会看到这个并说这个模型已经学会了“每栋房子的房间数”特征与价格输出呈正相关，或者房地产的 AGE 特征，由于其较低的绝对大小而未列出，比这前五个特征的重要性要低。由于我们的大脑喜欢讲故事的方式，很容易就把这些数字说得比证据支持的要多。例如，如果两个输入特征强相关，这种分析的一种失败方式是。

考虑一个假想的例子，其中相同的特征被意外地包含了两次。称它们为 FEAT1 和 FEAT2。假设学习到的两个特征的权重分别为 10 和 -5。你可能会倾向于认为增加 FEAT1 会导致输出增加，而 FEAT2 则相反。然而，由于这些特征是等价的，如果权重反转，模型将输出完全相同的值。

还有一个需要注意的地方是相关性与因果关系之间的区别。想象一个简单的模型，我们希望根据屋顶的湿度来预测外面下雨的程度。如果我们有一个屋顶湿度的测量值，我们可能可以预测过去一小时下了多少雨。但是，我们不能够向传感器泼水来制造雨！

练习

1. 在 2.1 节 中的硬编码时间估计问题之所以被选中，是因为数据大致上是线性的。其他数据集在拟合过程中将有不同的损失曲面和动态。您可能希望在这里尝试替换自己的数据，以探索模型的反应。您可能需要调整学习率、初始化或规范化来使模型收敛到一些有趣的东西。

2. 在 2.3.5 节 中，我们花了一些时间描述为什么归一化很重要以及如何将输入数据归一化为零均值和单位方差。你应该能够修改示例以去除归一化，并看到模型不再训练。你还应该能够修改归一化例程，例如，使均值不为 0 或标准偏差较低，但不是很低。有些归一化方法会奏效，有些会导致模型永远不收敛。

3. 众所周知，波士顿房价数据集的一些特征比其他特征更具有预测性。一些特征只是噪声，意味着它们不携带有用于预测房价的信息。如果我们只移除一个特征，我们应该保留哪个特征？如果我们要保留两个特征：我们该如何选择？尝试使用波士顿房价示例中的代码来探索这个问题。

4. 描述梯度下降如何通过以优于随机的方式更新权重来优化模型。

5. 波士顿房价示例打印出了绝对值最大的五个权重。尝试修改代码以打印与小权重相关联的特征。你能想象为什么这些权重很小吗？如果有人问你这些权重为什么是什么，你可以告诉他们什么？你会告诉那个人如何解释这些值的时候要注意什么？

总结

• 使用 TensorFlow.js 在五行 JavaScript 中构建、训练和评估一个简单的机器学习模型非常简单。

• 梯度下降，深度学习背后的基本算法结构，从概念上来说很简单，实际上只是指反复以小步骤更新模型参数，以使模型拟合最佳方向的计算方向。

• 模型的损失曲面展示了模型在一系列参数值的拟合程度。损失曲面通常无法计算，因为参数空间的维数很高，但思考一下并对机器学习的工作方式有直观的理解是很有意义的。

• 一个单独的密集层足以解决一些简单的问题，并且在房地产定价问题上可以获得合理的性能。

第三章：添加非线性：超越加权和

本章内容

• 什么是非线性，神经网络隐藏层中的非线性如何增强网络的容量并导致更好的预测准确性

• 超参数是什么，以及调整它们的方法

• 通过在输出层引入非线性进行二分类，以钓鱼网站检测示例为例介绍

• 多类分类以及它与二分类的区别，以鸢尾花示例介绍

在本章中，您将在第二章中奠定的基础上，允许您的神经网络学习更复杂的映射，从特征到标签。我们将介绍的主要增强是非线性——一种输入和输出之间的映射，它不是输入元素的简单加权和。非线性增强了神经网络的表征能力，并且当正确使用时，在许多问题上提高了预测准确性。我们将继续使用波士顿房屋数据集来说明这一点。此外，本章还将更深入地研究过拟合和欠拟合，以帮助您训练模型，这些模型不仅在训练数据上表现良好，而且在模型训练过程中没有见过的数据上达到良好的准确性，这才是模型质量的最终标准。

3.1. 非线性：它是什么，它有什么用处

让我们从上一章的波士顿房屋示例中继续进行。使用一个密集层，您看到训练模型导致的 MSE 对应于大约 5000 美元的误差估计。我们能做得更好吗？答案是肯定的。为了创建一个更好的波士顿房屋数据模型，我们为其添加了一个更多的密集层，如以下代码列表所示（来自波士顿房屋示例的 index.js）。

列表 3.1. 定义波士顿房屋问题的两层神经网络

export function multiLayerPerceptronRegressionModel1Hidden() {
  const model = tf.sequential();
  model.add(tf.layers.dense({
    inputShape: [bostonData.numFeatures],
    units: 50,
    activation: 'sigmoid',
    kernelInitializer: 'leCunNormal'        ***1***
  }));
  model.add(tf.layers.dense({units: 1}));   ***2***

  model.summary();                          ***3***
  return model;
};

• 1 指定了如何初始化内核值；参见 3.1.2 节讨论通过超参数优化选择的方式。

• 2 添加一个隐藏层

• 3 打印模型拓扑结构的文本摘要

要查看此模型的运行情况，请首先运行yarn && yarn watch命令，如第二章中所述。一旦网页打开，请点击 UI 中的 Train Neural Network Regressor (1 Hidden Layer)按钮，以开始模型的训练。

模型是一个双层网络。第一层是一个具有 50 个单元的稠密层。它也配置了自定义激活函数和内核初始化程序，我们将在第 3.1.2 节讨论。这一层是一个隐藏层，因为其输出不是直接从模型外部看到的。第二层是一个具有默认激活函数（线性激活）的稠密层，结构上与我们在第二章使用的纯线性模型中使用的同一层一样。这一层是一个输出层，因为其输出是模型的最终输出，并且是模型的predict()方法返回的内容。您可能已经注意到代码中的函数名称将模型称为多层感知器（MLP）。这是一个经常使用的术语，用来描述神经网络，其 1）拥有没有回路的简单拓扑结构（所谓前馈神经网络）和 2）至少有一层隐藏层。本章中您将看到的所有模型都符合这一定义。

清单 3.1 中的model.summary()调用是新的。这是一个诊断/报告工具，将 TensorFlow.js 模型的拓扑结构打印到控制台（在浏览器的开发者工具中或在 Node.js 的标准输出中）。以下是双层模型生成的结果：

_________________________________________________________________
Layer (type)                 Output shape              Param #
=================================================================
dense_Dense1 (Dense)         [null,50]                 650
 _________________________________________________________________
dense_Dense2 (Dense)         [null,1]                  51
=================================================================
Total params: 701
Trainable params: 701
Non-trainable params: 0

摘要中的关键信息包括：

• 层的名称和类型（第一列）。

• 每一层的输出形状（第二列）。这些形状几乎总是包含一个空维度作为第一（批处理）维度，代表着不确定和可变大小的批处理。

• 每层的权重参数数量（第三列）。这是一个计算各层权重的所有个别数量的计数。对于具有多个权重的层，这是跨所有权重求和。例如，本例中的第一个稠密层包含两个权重：形状为[12, 50]的内核和形状为[50]的偏置，导致12 * 50 + 50 = 650个参数。

• 模型的总权重参数数量（摘要底部），以及参数中可训练和不可训练的数量。到目前为止，我们看到的模型仅包含可训练参数，这些参数属于模型权重，在调用tf.Model.fit()时更新。在第五章讨论迁移学习和模型微调时，我们将讨论不可训练权重。

来自第二章纯线性模型的model.summary()输出如下。与线性模型相比，我们的双层模型包含大约 54 倍的权重参数。大部分额外权重来自于添加的隐藏层：

_________________________________________________________________
Layer (type)                 Output shape              Param #
=================================================================
dense_Dense3 (Dense)         [null,1]                  13
=================================================================
Total params: 13
Trainable params: 13
Non-trainable params: 0

因为两层模型包含更多层和权重参数，其训练和推断消耗更多的计算资源和时间。增加的成本是否值得准确度的提高？当我们为这个模型训练 200 个 epochs 时，我们得到的最终 MSE 在测试集上落在 14-15 的范围内（由于初始化的随机性而产生的变异性），相比之下，线性模型的测试集损失约为 25。我们的新模型最终的误差为美元 3,700-3,900，而纯线性尝试的误差约为 5,000 美元。这是一个显著的改进。

3.1.1. 建立神经网络非线性的直觉

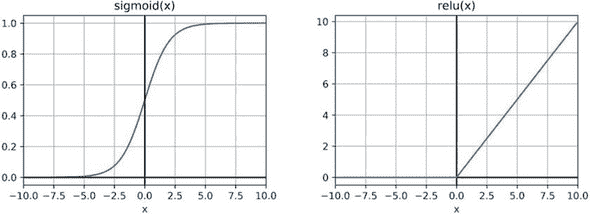
为什么准确度会提高呢？关键在于模型的增强复杂性，正如图 3.1 所示。首先，有一个额外的神经元层，即隐藏层。其次，隐藏层包含一个非线性的激活函数（在代码中指定为activation: 'sigmoid'），在图 3.1 的面板 B 中用方框表示。激活函数^([1])是逐元素的转换。sigmoid 函数是一种“压缩”非线性，它“压缩”了所有从负无穷到正无穷的实数值到一个更小的范围（在本例中是 0 到+1）。它的数学方程和图表如图 3.2 所示。让我们以隐藏的稠密层为例。假设矩阵乘法和加法的结果与偏差的结果是一个由以下随机值数组组成的 2D 张量：

¹

激活函数这个术语来源于对生物神经元的研究，它们通过动作电位（细胞膜上的电压尖峰）相互通信。一个典型的生物神经元从多个上游神经元接收输入，通过称为突触的接触点。上游神经元以不同的速率发出动作电位，这导致神经递质的释放和突触上离子通道的开闭。这反过来导致了接收神经元膜上的电压变化。这与稠密层中的单位所见到的加权和有些相似。只有当电位超过一定的阈值时，接收神经元才会实际产生动作电位（即被“激活”），从而影响下游神经元的状态。在这个意义上，典型生物神经元的激活函数与 relu 函数（图 3.2，右面板）有些相似，它在输入的某个阈值以下有一个“死区”，并且随着输入在阈值以上的增加而线性增加（至少到达某个饱和水平，这并不被 relu 函数所捕捉）。

[[1.0], [0.5], ..., [0.0]],

图 3.1。为波士顿住房数据集创建的线性回归模型（面板 A）和两层神经网络（面板 B）。为了清晰起见，在面板 B 中，我们将输入特征的数量从 12 个减少到 3 个，并将隐藏层的单元数量从 50 个减少到 5 个。每个模型只有一个输出单元，因为这些模型解决单变量（单目标数值）回归问题。面板 B 描绘了模型隐藏层的非线性（sigmoid）激活。

然后，通过将 sigmoid（S）函数应用于每个元素的 50 个元素中的每一个，得到密集层的最终输出，如下所示：

[[S(1.0)], [S(0.5)], ..., [S(0.0)]] = [[0.731], [0.622], ..., [0.0]]

为什么这个函数被称为非线性？直观地说，激活函数的图形不是一条直线。例如，sigmoid 是一条曲线（图 3.2，左侧面板），而 relu 是两条线段的拼接（图 3.2，右侧面板）。尽管 sigmoid 和 relu 是非线性的，但它们的一个特性是它们在每个点上都是平滑且可微的，这使得可以通过它们进行反向传播^([2])。如果没有这个特性，就不可能训练包含这种激活函数的层的模型。

²

如果需要回顾反向传播，请参阅第 2.2.2 节。

图 3.2。用于深度神经网络的两个常用非线性激活函数。左：sigmoid 函数 S(x) = 1 / (1 + e ^ -x)。右：修正线性单元（relu）函数 relu(x) = {0:x < 0, x:x >= 0}

除了 sigmoid 函数之外，在深度学习中还经常使用一些其他类型的可微非线性函数。其中包括 relu 和双曲正切函数（tanh）。在后续的例子中遇到它们时，我们将对它们进行详细描述。

非线性和模型容量

为什么非线性能够提高我们模型的准确性？非线性函数使我们能够表示更多样化的输入-输出关系。现实世界中的许多关系大致是线性的，比如我们在上一章中看到的下载时间问题。但是，还有许多其他关系不是线性的。很容易构想出非线性关系的例子。考虑一个人的身高与年龄之间的关系。身高仅在某一点之前大致与年龄线性变化，之后会弯曲并趋于稳定。另一个完全合理的情景是，房价可以与社区犯罪率呈负相关，但前提是犯罪率在某一范围内。一个纯线性模型，就像我们在上一章中开发的模型一样，无法准确地建模这种类型的关系，而 sigmoid 非线性则更适合于建模这种关系。当然，犯罪率-房价关系更像是一个倒置的（下降的）sigmoid 函数，而不是左侧面板中原始的增长函数。但是我们的神经网络可以毫无问题地建模这种关系，因为 sigmoid 激活前后都是由可调节权重的线性函数。

但是，通过将线性激活替换为非线性激活（比如 sigmoid），我们会失去学习数据中可能存在的任何线性关系的能力吗？幸运的是，答案是否定的。这是因为 sigmoid 函数的一部分（靠近中心的部分）非常接近一条直线。其他经常使用的非线性激活函数，比如 tanh 和 relu，也包含线性或接近线性的部分。如果输入的某些元素与输出的某些元素之间的关系大致是线性的，那么一个带有非线性激活函数的密集层完全可以学习到使用激活函数的接近线性部分的正确权重和偏差。因此，向密集层添加非线性激活会导致它能够学习的输入-输出关系的广度增加。

此外，非线性函数与线性函数不同之处在于级联非线性函数会导致更丰富的非线性函数集合。这里，“级联”是指将一个函数的输出作为另一个函数的输入。假设有两个线性函数，

f(x) = k1 * x + b1

和

g(x) = k2 * x + b2

级联两个函数等同于定义一个新函数h：

h(x) = g(f(x)) = k2 * (k1 * x + b1) + b2 = (k2 * k1) * x + (k2 * b1 + b2)

如您所见，h仍然是一个线性函数。它的核（斜率）和偏差（截距）与f1和f2的不同。斜率现在是(k2 * k1)，偏差现在是(k2 * b1 + b2)。级联任意数量的线性函数始终会产生一个线性函数。

但是，请考虑一个经常使用的非线性激活函数：relu。在图 3.3 的底部，我们说明了当您级联两个具有线性缩放的 relu 函数时会发生什么。通过级联两个缩放的 relu 函数，我们得到一个看起来根本不像 relu 的函数。它具有一个新形状（在这种情况下，是由两个平坦部分包围的向下倾斜的部分）。进一步级联阶跃函数与其他 relu 函数将得到一组更多样化的函数，例如“窗口”函数，由多个窗口组成的函数，窗口叠加在更宽的窗口上的函数等（未显示在图 3.3 中）。通过级联 relu 等非线性函数，您可以创建出非常丰富的一系列函数形状。但这与神经网络有什么关系呢？实质上，神经网络是级联函数。神经网络的每一层都可以看作是一个函数，而将这些层堆叠起来就相当于级联这些函数，形成更复杂的函数，即神经网络本身。这应该清楚地说明为什么包含非线性激活函数会增加模型能够学习的输入-输出关系范围。这也让你直观地理解了常用技巧“向深度神经网络添加更多层”以及为什么它通常（但并非总是！）会导致更能拟合数据集的模型。

图 3.3。级联线性函数（顶部）和非线性函数（底部）。级联线性函数总是导致线性函数，尽管具有新的斜率和截距。级联非线性函数（例如 relu 在本例中）会导致具有新形状的非线性函数，例如本例中的“向下阶跃”函数。这说明了为什么在神经网络中使用非线性激活函数以及级联它们会导致增强的表示能力（即容量）。

机器学习模型能够学习的输入-输出关系范围通常被称为模型的容量。从先前关于非线性的讨论中，我们可以看出，具有隐藏层和非线性激活函数的神经网络与线性回归器相比具有更大的容量。这就解释了为什么我们的两层网络在测试集准确度方面比线性回归模型表现出更好的效果。

你可能会问，由于级联非线性激活函数会导致更大的容量（如图 3.3 的底部所示），我们是否可以通过向神经网络添加更多的隐藏层来获得更好的波士顿房价问题模型？multiLayerPerceptronRegressionModel2Hidden()函数位于 index.js 中，它连接到标题为训练神经网络回归器（2 个隐藏层）的按钮。该函数确实执行了这样的操作。请参阅以下代码摘录（来自波士顿房价示例的 index.js）。

列表 3.2. 为波士顿房屋问题定义一个三层神经网络

export function multiLayerPerceptronRegressionModel2Hidden() {
  const model = tf.sequential();
  model.add(tf.layers.dense({               ***1***
    inputShape: [bostonData.numFeatures],   ***1***
    units: 50,                              ***1***
    activation: 'sigmoid',                  ***1***
    kernelInitializer: 'leCunNormal'        ***1***
  }));                                      ***1***
  model.add(tf.layers.dense({               ***2***
    units: 50,                              ***2***
    activation: 'sigmoid',                  ***2***
    kernelInitializer: 'leCunNormal'        ***2***
  }));                                      ***2***
  model.add(tf.layers.dense({units: 1}));

  model.summary();                          ***3***
  return model;
};

• 1 添加第一个隐藏层

• 2 添加另一个隐藏层

• 3 展示模型拓扑的文本摘要

在summary()打印输出中（未显示），你可以看到该模型包含三层——比 列表 3.1 中的模型多一层。它也具有显著更多的参数：3,251 个，相比两层模型中的 701 个。额外的 2,550 个权重参数是由于包括了第二个隐藏层造成的，它由形状为[50, 50]的内核和形状为[50]的偏差组成。

重复训练模型多次，我们可以对三层网络最终测试集（即评估）MSE 的范围有所了解：大致为 10.8–13.4。这相当于对$3,280–$3,660 的误估，超过了两层网络的$3,700–$3,900。因此，我们通过添加非线性隐藏层再次提高了模型的预测准确性，增强了其容量。

避免将层堆叠而没有非线性的谬误

另一种看到非线性激活对改进波士顿房屋模型的重要性的方式是将其从模型中移除。列表 3.3 与 列表 3.1 相同，只是注释掉了指定 S 型激活函数的一行。移除自定义激活会导致该层具有默认的线性激活。模型的其他方面，包括层数和权重参数数量，都不会改变。

列表 3.3. 没有非线性激活的两层神经网络

export function multiLayerPerceptronRegressionModel1Hidden() {
  const model = tf.sequential();
  model.add(tf.layers.dense({
    inputShape: [bostonData.numFeatures],
    units: 50,
    // activation: 'sigmoid',          ***1***
    kernelInitializer: 'leCunNormal'
  }));
  model.add(tf.layers.dense({units: 1}));

  model.summary();
  return model;
};

• 1 禁用非线性激活函数

这种改变如何影响模型的学习？通过再次点击 UI 中的 Train Neural Network Regressor（1 Hidden Layer）按钮，你可以得知测试集上的 MSE 上升到约 25，而当 S 型激活包含时大约为 14–15 的范围。换句话说，没有 S 型激活的两层模型表现与一层线性回归器大致相同！

这证实了我们关于级联线性函数的推理。通过从第一层中移除非线性激活，我们最终得到了一个两个线性函数级联的模型。正如我们之前展示的，结果是另一个线性函数，而模型的容量没有增加。因此，我们最终的准确性与线性模型大致相同并不奇怪。这提出了构建多层神经网络的常见“陷阱”：一定要在隐藏层中包括非线性激活。没有这样做会导致计算资源和时间的浪费，并有潜在的增加数值不稳定性（观察 图 3.4 的面板 B 中更加不稳定的损失曲线）。稍后，我们将看到这不仅适用于密集层，还适用于其他层类型，如卷积层。

图 3.4. 比较使用（面板 A）和不使用（面板 B）Sigmoid 激活的训练结果。请注意，去除 Sigmoid 激活会导致训练、验证和评估集上的最终损失值更高（与之前的纯线性模型相当）且损失曲线不够平滑。请注意，两个图之间的 y 轴刻度是不同的。

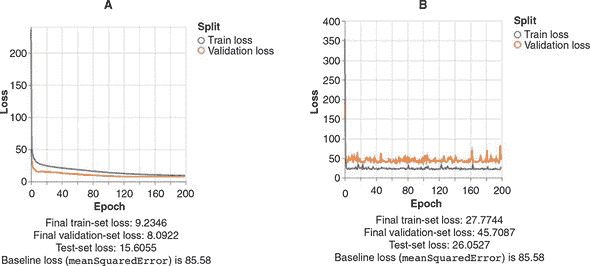
非线性和模型可解释性

在第二章中，我们展示了一旦在波士顿房屋数据集上训练了一个线性模型，我们就可以检查其权重并以相当有意义的方式解释其各个参数。例如，与“每个住宅的平均房间数”特征相对应的权重具有正值，而与“犯罪率”特征相对应的权重具有负值。这些权重的符号反映了房价与相应特征之间的预期正相关或负相关关系。它们的大小也暗示了模型对各种特征的相对重要性。鉴于您刚刚在本章学到的内容，一个自然的问题是：使用一个或多个隐藏层的非线性模型，是否仍然可能提出可理解和直观的权重值解释？

访问权重值的 API 在非线性模型和线性模型之间完全相同：您只需在模型对象或其组成层对象上使用getWeights()方法。以清单 3.1 中的 MLP 为例——您可以在模型训练完成后（model.fit()调用之后）插入以下行：

model.layers[0].getWeights()[0].print();

这行打印了第一层（即隐藏层）的核心值。这是模型中的四个权重张量之一，另外三个是隐藏层的偏置和输出层的核心和偏置。关于打印输出的一件事值得注意的是，它的大小比我们打印线性模型的核心时要大：

Tensor
    [[-0.5701274, -0.1643915, -0.0009151, ..., 0.313205  , -0.3253246],
     [-0.4400523, -0.0081632, -0.2673715, ..., 0.1735748 , 0.0864024 ],
     [0.6294659 , 0.1240944 , -0.2472516, ..., 0.2181769 , 0.1706504 ],
     [0.9084488 , 0.0130388 , -0.3142847, ..., 0.4063887 , 0.2205501 ],
     [0.431214  , -0.5040522, 0.1784604 , ..., 0.3022115 , -0.1997144],
     [-0.9726604, -0.173905 , 0.8167523 , ..., -0.0406454, -0.4347956],
     [-0.2426955, 0.3274118 , -0.3496988, ..., 0.5623314 , 0.2339328 ],
     [-1.6335299, -1.1270424, 0.618491  , ..., -0.0868887, -0.4149215],
     [-0.1577617, 0.4981289 , -0.1368523, ..., 0.3636355 , -0.0784487],
     [-0.5824679, -0.1883982, -0.4883655, ..., 0.0026836 , -0.0549298],
     [-0.6993552, -0.1317919, -0.4666585, ..., 0.2831602 , -0.2487895],
     [0.0448515 , -0.6925298, 0.4945385 , ..., -0.3133179, -0.0241681]]

这是因为隐藏层由 50 个单元组成，导致权重大小为[18, 50]。与线性模型的核心中的12 + 1 = 13个参数相比，该核心有 900 个单独的权重参数。我们能赋予每个单独的权重参数一定的含义吗？一般来说，答案是否定的。这是因为从隐藏层的 50 个输出中很难找到任何一个的明显含义。这些是高维空间的维度，使模型能够学习（自动发现）其中的非线性关系。人类大脑在跟踪这种高维空间中的非线性关系方面并不擅长。一般来说，很难用通俗易懂的几句话来描述隐藏层每个单元的作用，或者解释它如何对深度神经网络的最终预测做出贡献。

此处的模型只有一个隐藏层。当有多个隐藏层堆叠在一起时（就像在清单 3.2 中定义的模型中一样），关系变得更加模糊和更难描述。尽管有研究努力寻找解释深度神经网络隐藏层含义的更好方法，^{([3])并且针对某些类别的模型正在取得进展，}([4])但可以说，深度神经网络比浅层神经网络和某些类型的非神经网络机器学习模型（如决策树）更难解释。通过选择深度模型而不是浅层模型，我们基本上是在为更大的模型容量交换一些可解释性。

³

Marco Tulio Ribeiro，Sameer Singh 和 Carlos Guestrin，“局部可解释的模型无关解释（LIME）：简介”，O’Reilly，2016 年 8 月 12 日，mng.bz/j5vP。

⁴

Chris Olah 等，“可解释性的基本构建块”，Distill，2018 年 3 月 6 日，distill.pub/2018/building-blocks/。

3.1.2. 超参数和超参数优化

我们在清单 3.1 和 3.2 中对隐藏层的讨论一直侧重于非线性激活（sigmoid）。然而，该层的其他配置参数对于确保模型的良好训练结果也很重要。这些包括单位数量（50）和内核的 'leCunNormal' 初始化。后者是根据输入的大小生成进入内核初始值的随机数的特殊方式。它与默认的内核初始化器（'glorotNormal'）不同，后者使用输入和输出的大小。自然的问题是：为什么使用这个特定的自定义内核初始化器而不是默认的？为什么使用 50 个单位（而不是，比如，30 个）？通过反复尝试各种参数组合，这些选择是为了确保通过尽可能多地尝试各种参数组合获得最佳或接近最佳的模型质量。

参数，如单位数量、内核初始化器和激活函数，是模型的超参数。名称“超参数”表明这些参数与模型的权重参数不同，后者在训练期间通过反向传播自动更新（即，Model.fit() 调用）。一旦为模型选择了超参数，它们在训练过程中不会改变。它们通常确定权重参数的数量和大小（例如，考虑密集层的 units 字段）、权重参数的初始值（考虑 kernelInitializer 字段）以及它们在训练期间如何更新（考虑传递给 Model.compile() 的 optimizer 字段）。因此，它们位于高于权重参数的层次上。因此得名“超参数”。

除了层的大小和权重初始化器的类型之外，模型及其训练还有许多其他类型的超参数，例如

• 模型中的密集层数量，比如 listings 3.1 和 3.2 中的那些

• 用于密集层核的初始化器的类型

• 是否使用任何的权重正则化（参见第 8.1 节），如果是，则是正则化因子

• 是否包括任何的 dropout 层（例如，参见第 4.3.2 节），如果是，则是多少的 dropout 率

• 用于训练的优化器的类型（例如，'sgd'与'adam'之间的区别；参见 info box 3.1）

• 训练模型的时期数是多少

• 优化器的学习率

• 是否应该随着训练的进行逐渐减小优化器的学习率，如果是，以什么速度

• 训练的批次大小

列出的最后五个例子有些特殊，因为它们与模型本身的架构无关；相反，它们是模型训练过程的配置。然而，它们会影响训练的结果，因此被视为超参数。对于包含更多不同类型层的模型（例如，在第四章、第五章和第九章中讨论的卷积和循环层），还有更多可能可调整的超参数。因此，即使是一个简单的深度学习模型可能也有几十个可调整的超参数是很清楚的。

选择良好的超参数值的过程称为超参数优化或超参数调整。超参数优化的目标是找到一组参数，使训练后验证损失最低。不幸的是，目前没有一种确定的算法可以确定给定数据集和涉及的机器学习任务的最佳超参数。困难在于许多超参数是离散的，因此验证损失值对它们不是可微的。例如，密集层中的单元数和模型中的密集层数是整数；优化器的类型是一个分类参数。即使对于那些是连续的超参数（例如，正则化因子），对它们进行训练期间的梯度跟踪通常也是计算上过于昂贵的，因此在这些超参数空间中执行梯度下降实际上并不可行。超参数优化仍然是一个活跃的研究领域，深度学习从业者应该注意。

鉴于缺乏一种标准的、开箱即用的超参数优化方法或工具，深度学习从业者通常采用以下三种方法。首先，如果手头的问题类似于一个经过深入研究的问题（比如，你可以在本书中找到的任何示例），你可以开始应用类似的模型来解决你的问题，并“继承”超参数。稍后，你可以在以该起点为中心的相对较小的超参数空间中进行搜索。

其次，有足够经验的从业者可能对于给定问题的合理良好的超参数有直觉和教育性的猜测。即使是这样主观的选择几乎从来都不是最佳的——它们形成了良好的起点，并且可以促进后续的微调。

第三，对于只有少量需要优化的超参数的情况（例如少于四个），我们可以使用格点搜索——即，穷举地迭代一些超参数组合，对每一个组合训练一个模型至完成，记录验证损失，并取得验证损失最低的超参数组合。例如，假设唯一需要调整的两个超参数是 1）密集层中的单元数和 2）学习率；你可以选择一组单元（{10, 20, 50, 100, 200}）和一组学习率（{1e-5, 1e-4, 1e-3, 1e-2}），并对两组进行交叉，从而得到一共5 * 4 = 20个要搜索的超参数组合。如果你要自己实现格点搜索，伪代码可能看起来像以下清单。

清单 3.4. 用于简单超参数格点搜索的伪代码

function hyperparameterGridSearch():
  for units of [10, 20, 50, 100, 200]:
    for learningRate  of [1e-5, 1e-4, 1e-3, 1e-2]:
       Create a model using whose dense layer consists of `units` units
       Train the model with an optimizer with `learningRate`
       Calculate final validation loss as validationLoss
       if validationLoss < minValidationLoss
         minValidationLoss := validationLoss
         bestUnits := units
         bestLearningRate := learningRate

  return [bestUnits, bestLearningRate]

这些超参数的范围是如何选择的？嗯，深度学习无法提供正式答案的另一个地方。这些范围通常基于深度学习从业者的经验和直觉。它们也可能受到计算资源的限制。例如，一个单位过多的密集层可能导致模型训练过程太慢或推断时运行太慢。

通常情况下，需要优化的超参数数量较多，以至于在指数增长的超参数组合数量上进行搜索变得计算上过于昂贵。在这种情况下，应该使用比格点搜索更复杂的方法，如随机搜索^{([5])和贝叶斯}([6])方法。

⁵

James Bergstra 和 Yoshua Bengio，“超参数优化的随机搜索”，机器学习研究杂志，2012 年，第 13 卷，第 281–305 页，mng.bz/WOg1。

⁶

Will Koehrsen，“贝叶斯超参数优化的概念解释”，Towards Data Science，2018 年 6 月 24 日，mng.bz/8zQw。

3.2. 输出的非线性：用于分类的模型

我们到目前为止看到的两个例子都是回归任务，我们试图预测一个数值（如下载时间或平均房价）。然而，机器学习中另一个常见的任务是分类。一些分类任务是二元分类，其中目标是对一个是/否问题的答案。技术世界充满了这种类型的问题，包括

• 是否给定的电子邮件是垃圾邮件

• 是否给定的信用卡交易是合法的还是欺诈的

• 是否给定的一秒钟音频样本包含特定的口语单词

• 两个指纹图像是否匹配（来自同一个人的同一个手指）

另一种分类问题是多类别分类任务，对此类任务也有很多例子：

• 一篇新闻文章是关于体育、天气、游戏、政治还是其他一般话题

• 一幅图片是猫、狗、铲子等等

• 给定电子笔的笔触数据，确定手写字符是什么

• 在使用机器学习玩一个类似 Atari 的简单视频游戏的场景中，确定游戏角色应该向四个可能的方向之一（上、下、左、右）前进，给定游戏的当前状态

3.2.1. 什么是二元分类？

我们将从一个简单的二元分类案例开始。给定一些数据，我们想要一个是/否的决定。对于我们的激励示例，我们将谈论钓鱼网站数据集。任务是，给定关于网页和其 URL 的一组特征，预测该网页是否用于钓鱼（伪装成另一个站点，目的是窃取用户的敏感信息）。

⁷

Rami M. Mohammad, Fadi Thabtah, 和 Lee McCluskey，“Phishing Websites Features,” mng.bz/E1KO。

数据集包含 30 个特征，所有特征都是二元的（表示值为-1 和 1）或三元的（表示为-1、0 和 1）。与我们为波士顿房屋数据集列出所有单个特征不同，这里我们提供一些代表性的特征：

• HAVING_IP_ADDRESS—是否使用 IP 地址作为域名的替代（二进制值：{-1, 1}）

• SHORTENING_SERVICE—是否使用 URL 缩短服务（二进制值：{1, -1}）

• SSLFINAL_STATE—URL 是否使用 HTTPS 并且发行者是受信任的，它是否使用 HTTPS 但发行者不受信任，或者没有使用 HTTPS（三元值：{-1, 0, 1}）

数据集由大约 5500 个训练示例和相同数量的测试示例组成。在训练集中，大约有 45%的示例是正面的（真正的钓鱼网页）。在测试集中，正面示例的百分比大约是相同的。

这只是最容易处理的数据集类型——数据中的特征已经在一致的范围内，因此无需对其均值和标准偏差进行归一化，就像我们为波士顿房屋数据集所做的那样。此外，相对于特征数量和可能预测数量（两个——是或否），我们有大量的训练示例。总的来说，这是一个很好的健全性检查，表明这是一个我们可以处理的数据集。如果我们想要花更多时间研究我们的数据，我们可能会进行成对特征相关性检查，以了解是否有冗余信息；但是，这是我们的模型可以容忍的。

由于我们的数据与我们用于波士顿房屋（后归一化）的数据相似，我们的起始模型基于相同的结构。此问题的示例代码可在 tfjs-examples 存储库的 website-phishing 文件夹中找到。您可以按照以下方式查看和运行示例：

git clone https://github.com/tensorflow/tfjs-examples.git
cd tfjs-examples/website-phishing
yarn && yarn watch

列表 3.5. 为钓鱼检测定义二分类模型（来自 index.js）

const model = tf.sequential();
model.add(tf.layers.dense({
  inputShape: [data.numFeatures],
  units: 100,
  activation: 'sigmoid'
}));
model.add(tf.layers.dense({units: 100, activation: 'sigmoid'}));
model.add(tf.layers.dense({units: 1, activation: 'sigmoid'}));
model.compile({
  optimizer: 'adam',
  loss: 'binaryCrossentropy',
  metrics: ['accuracy']
});

这个模型与我们为波士顿房屋问题构建的多层网络有很多相似之处。它以两个隐藏层开始，两者都使用 sigmoid 激活。最后（输出）有确切的 1 个单元，这意味着模型为每个输入示例输出一个数字。然而，这里的一个关键区别是，我们用于钓鱼检测的模型的最后一层具有 sigmoid 激活，而不是波士顿房屋模型中的默认线性激活。这意味着我们的模型受限于只能输出介于 0 和 1 之间的数字，这与波士顿房屋模型不同，后者可能输出任何浮点数。

之前，我们已经看到 sigmoid 激活对隐藏层有助于增加模型容量。但是为什么在这个新模型的输出处使用 sigmoid 激活？这与我们手头问题的二分类特性有关。对于二分类，我们通常希望模型产生正类别的概率猜测——也就是说，模型“认为”给定示例属于正类别的可能性有多大。您可能还记得高中数学中的知识，概率始终是介于 0 和 1 之间的数字。通过让模型始终输出估计的概率值，我们获得了两个好处：

• 它捕获了对分配的分类的支持程度。sigmoid值为0.5表示完全不确定性，其中每个分类都得到了同等的支持。值为0.6表示虽然系统预测了正分类，但支持程度很低。值为0.99表示模型非常确定该示例属于正类，依此类推。因此，我们使得将模型的输出转换为最终答案变得简单而直观（例如，只需在给定值处对输出进行阈值处理，例如0.5）。现在想象一下，如果模型的输出范围可能变化很大，那么找到这样的阈值将会有多难。

• 我们还使得更容易构造一个可微的损失函数，它根据模型的输出和真实的二进制目标标签产生一个衡量模型错失程度的数字。至于后者，当我们检查该模型使用的实际二元交叉熵时，我们将会更详细地阐述。

但是，问题是如何将神经网络的输出强制限制在[0, 1]范围内。神经网络的最后一层通常是一个密集层，它对其输入执行矩阵乘法(matMul)和偏置加法(biasAdd)操作。在matMul或biasAdd操作中都没有固有的约束，以保证结果在[0, 1]范围内。将sigmoid等压缩非线性添加到matMul和biasAdd的结果中是实现[0, 1]范围的一种自然方法。

清单 3.5 中代码的另一个新方面是优化器的类型：'adam'，它与之前示例中使用的'sgd'优化器不同。adam与sgd有何不同？正如你可能还记得上一章第 2.2.2 节所述，sgd优化器总是将通过反向传播获得的梯度乘以一个固定数字（学习率乘以-1）以计算模型权重的更新。这种方法有一些缺点，包括当选择较小的学习率时，收敛速度较慢，并且当损失（超）表面的形状具有某些特殊属性时，在权重空间中出现“之”形路径。adam优化器旨在通过以一种智能方式使用梯度的历史（来自先前的训练迭代）的乘法因子来解决这些sgd的缺点。此外，它对不同的模型权重参数使用不同的乘法因子。因此，与一系列深度学习模型类型相比，adam通常导致更好的收敛性和对学习率选择的依赖性较小；因此，它是优化器的流行选择。TensorFlow.js 库提供了许多其他优化器类型，其中一些也很受欢迎（如rmsprop）。信息框 3.1 中的表格提供了它们的简要概述。

TensorFlow.js 支持的优化器

下表总结了 TensorFlow.js 中最常用类型的优化器的 API，以及对每个优化器的简单直观解释。

TensorFlow.js 中常用的优化器及其 API

名称	API（字符串）	API（函数）	描述
随机梯度下降（SGD）	‘sgd’	tf.train.sgd	最简单的优化器，始终使用学习率作为梯度的乘子
Momentum	‘momentum’	tf.train.momentum	以一种方式累积过去的梯度，使得对于某个权重参数的更新在过去的梯度更多地朝着同一方向时变得更快，并且当它们在方向上发生大变化时变得更慢
RMSProp	‘rmsprop’	tf.train.rmsprop	通过跟踪模型不同权重参数的最近梯度的均方根（RMS）值的历史记录，为不同的权重参数设置不同的乘法因子；因此得名
AdaDelta	‘adadelta’	tf.train.adadelta	类似于 RMSProp，以一种类似的方式为每个单独的权重参数调整学习率
ADAM	‘adam’	tf.train.adam	可以理解为 AdaDelta 的自适应学习率方法和动量方法的结合
AdaMax	‘adamax’	tf.train.adamax	类似于 ADAM，但使用稍微不同的算法跟踪梯度的幅度

一个明显的问题是，针对你正在处理的机器学习问题和模型，应该使用哪种优化器。不幸的是，在深度学习领域尚无共识（这就是为什么 TensorFlow.js 提供了上表中列出的所有优化器！）。在实践中，你应该从流行的优化器开始，包括 adam 和 rmsprop。在有足够的时间和计算资源的情况下，你还可以将优化器视为超参数，并通过超参数调整找到为你提供最佳训练结果的选择（参见 section 3.1.2）。

3.2.2. 衡量二元分类器的质量：准确率、召回率、准确度和 ROC 曲线

在二元分类问题中，我们发出两个值之一——0/1、是/否等等。在更抽象的意义上，我们将讨论正例和负例。当我们的网络进行猜测时，它要么正确要么错误，所以我们有四种可能的情况，即输入示例的实际标签和网络输出，如 table 3.1 所示。

表 3.1. 二元分类问题中的四种分类结果类型

		预测
		正类
	正类	真正例（TP）
	负类	假正例（FP）

真正的正例（TP）和真正的负例（TN）是模型预测出正确答案的地方；假正例（FP）和假负例（FN）是模型出错的地方。如果我们用计数填充这四个单元格，我们就得到了一个混淆矩阵；表 3.2 显示了我们钓鱼检测问题的一个假设性混淆矩阵。

表 3.2. 一个假设的二元分类问题的混淆矩阵

		预测
		正例
	正例	4
	负例	1

在我们假设的钓鱼示例结果中，我们看到我们正确识别了四个钓鱼网页，漏掉了两个，而且有一个误报。现在让我们来看看用于表达这种性能的不同常见指标。

准确率是最简单的度量标准。它量化了多少百分比的示例被正确分类：

Accuracy = (#TP + #TN) / #examples = (#TP + #TN) / (#TP + #TN + #FP + #FN)

在我们特定的例子中，

Accuracy = (4 + 93) / 100 = 97%

准确率是一个易于沟通和易于理解的概念。然而，它可能会具有误导性——在二元分类任务中，我们通常没有相等分布的正负例。我们通常处于这样的情况：正例要远远少于负例（例如，大多数链接不是钓鱼网站，大多数零件不是有缺陷的，等等）。如果 100 个链接中只有 5 个是钓鱼的，我们的网络可以总是预测为假，并获得 95% 的准确率！这样看来，准确率似乎是我们系统的一个非常糟糕的度量。高准确率听起来总是很好，但通常会误导人。监视准确率是件好事，但作为损失函数使用则是一件非常糟糕的事情。

下一对指标试图捕捉准确率中缺失的微妙之处——精确率和召回率。在接下来的讨论中，我们通常考虑的是一个正例意味着需要进一步的行动——一个链接被标记，一篇帖子被标记为需要手动审查——而负例表示现状不变。这些指标专注于我们的预测可能出现的不同类型的“错误”。

精确率是模型预测的正例中实际为正例的比率：

precision = #TP / (#TP + #FP)

根据我们混淆矩阵的数字，我们将计算

precision = 4 / (4 + 1) = 80%

与准确率类似，通常可以操纵精确率。例如，您可以通过仅将具有非常高 S 型输出（例如 >0.95，而不是默认的 >0.5）的输入示例标记为正例，从而使您的模型非常保守地发出正面预测。这通常会导致精确率提高，但这样做可能会导致模型错过许多实际的正例（将它们标记为负例）。这最后一个成本被常与精确率配合使用并补充的度量所捕获，即召回率。

召回率是模型将实际正例分类为正例的比率：

recall = #TP / (#TP + #FN)

根据示例数据，我们得到了一个结果

recall = 4 / (4 + 2) = 66.7%

在样本集中所有阳性样本中，模型发现了多少个？通常会有一个有意识的决定，即接受较高的误报率以降低遗漏的可能性。为了优化这一指标，你可以简单地声明所有样本为阳性；由于假阳性不进入计算，因此你可以在降低精确度的代价下获得 100%的召回率。

我们可以看到，制作一个在准确度、召回率或精确度上表现出色的系统相当容易。在现实世界中的二元分类问题中，同时获得良好的精确度和召回率通常很困难。（如果这样做很容易，你就会面临一个简单的问题，可能根本不需要使用机器学习。）精确度和召回率涉及在对正确答案存在根本不确定的复杂区域调整模型。你会看到更多细致和组合的指标，如在 X%召回率下的精确度，其中 X 通常为 90%——如果我们调整到至少发现 X%的阳性样本，精确度是多少？例如，在图 3.5 中，我们看到经过 400 个轮次的训练后，当模型的概率输出门槛设为 0.5 时，我们的钓鱼检测模型能够达到 96.8%的精确度和 92.9%的召回率。

图 3.5。训练模型用于钓鱼网页检测的一轮结果示例。注意底部的各种指标：精确度、召回率和 FPR。曲线下面积（AUC）在 3.2.3 节中讨论。

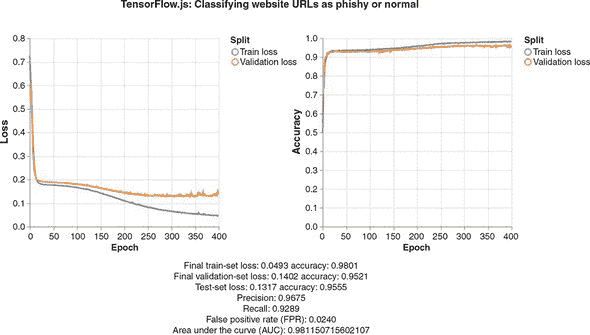
如我们已略有提及的，一个重要的认识是，对正预测的选择，不需要在 sigmoid 输出上设置恰好为 0.5 的门槛。事实上，根据情况，它可能最好设定为 0.5 以上（但小于 1）或 0.5 以下（但大于 0）。降低门槛使模型在将输入标记为阳性时更加自由，这会导致更高的召回率但可能降低精确度。另一方面，提高门槛使模型在将输入标记为阳性时更加谨慎，通常会导致更高的精确度但可能降低召回率。因此，我们可以看到精确度和召回率之间存在权衡，这种权衡很难用我们迄今讨论过的任何一种指标来量化。幸运的是，二元分类研究的丰富历史为我们提供了更好的方式来量化和可视化这种权衡关系。我们接下来将讨论的 ROC 曲线是这种常用的工具之一。

3.2.3。ROC 曲线：展示二元分类中的权衡

ROC 曲线被用于广泛的工程问题，其中包括二分类或特定类型事件的检测。全名“接收者操作特性”是一个来自雷达早期的术语。现在，你几乎看不到这个扩展名了。图 3.6 是我们应用程序的一个样本 ROC 曲线。

图 3.6. 在钓鱼检测模型训练期间绘制的一组样本 ROC 曲线。每条曲线对应不同的周期数。这些曲线显示了二分类模型随着训练的进展而逐渐改进的质量。

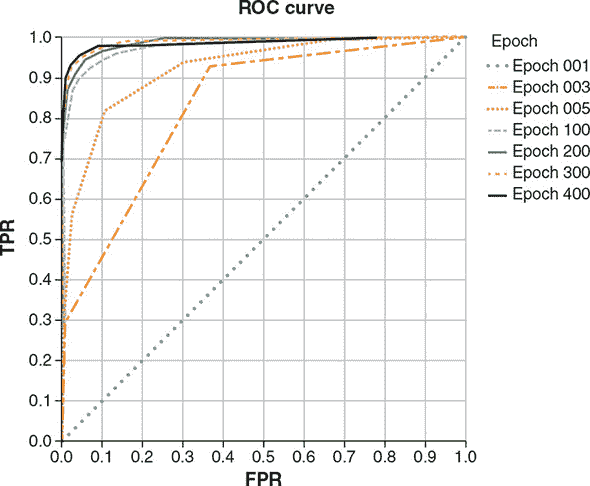
正如你可能已经在图 3.6 的坐标轴标签中注意到的，ROC 曲线并不是通过将精确度和召回率指标相互绘制得到的。相反，它们是基于两个稍微不同的指标。ROC 曲线的横轴是假阳性率（FPR），定义为

FPR = #FP / (#FP + #TN)

ROC 曲线的纵轴是真阳性率（TPR），定义为

TPR = #TP / (#TP + #FN) = recall

TPR 与召回率具有完全相同的定义，只是使用了不同的名称。然而，FPR 是一些新的东西。分母是实际类别为负的案例数量；分子是所有误报的数量。换句话说，FPR 是将实际上是负的案例错误分类为正的比例，这是一个常常被称为*虚警（false alarm）*的概率。表 3.3 总结了在二分类问题中遇到的最常见的指标。

表 3.3. 二分类问题中常见的指标

指标名称	定义	ROC 曲线或精确度/召回率曲线中的使用方式
准确度（Accuracy）	(#TP + #TN) / (#TP + #TN + # FP + #FN)	（ROC 曲线中不使用）
精确度（Precision）	#TP / (#TP + #FP)	精确度/召回率曲线的纵轴
召回率/灵敏度/真阳性率（TPR）	#TP / (#TP + #FN)	ROC 曲线的纵轴（如图 3.6）或精确度/召回率曲线的横轴
假阳性率（False positive rate，FPR）	#FP / (#FP + #TN)	ROC 曲线的横轴（见图 3.6）
曲线下面积（Area under the curve，AUC）	将 ROC 曲线的数值积分计算得出；查看代码示例 3.7 以获取示例	（ROC 曲线不使用，而是从 ROC 曲线计算得到）

图 3.6 中的七条 ROC 曲线分别绘制于七个不同的训练周期的开头，从第一个周期 (周期 001) 到最后一个周期 (周期 400)。每条曲线都是基于模型在测试数据上的预测结果（而不是训练数据）创建的。代码清单 3.6 显示了如何利用 Model.fit() API 中的 onEpochBegin 回调函数详细实现此过程。这种方法使您可以在训练过程中执行有趣的分析和可视化，而不需要编写 for 循环或使用多个 Model.fit() 调用。

代码清单 3.6 使用回调函数在模型训练中间绘制 ROC 曲线

  await model.fit(trainData.data, trainData.target, {
    batchSize,
    epochs,
    validationSplit: 0.2,
    callbacks: {
    onEpochBegin: async (epoch) => {
        if ((epoch + 1)% 100 === 0 ||
                        epoch === 0 || epoch === 2 || epoch === 4) {
                                                            ***1***
            const probs = model.predict(testData.data);
            drawROC(testData.target, probs, epoch);
        }
      },
      onEpochEnd: async (epoch, logs) => {
        await ui.updateStatus(
                `Epoch ${epoch + 1} of ${epochs} completed.`);
        trainLogs.push(logs);
        ui.plotLosses(trainLogs);
        ui.plotAccuracies(trainLogs);
      }
    }
  });

• 1 每隔几个周期绘制 ROC 曲线。

函数 drawROC() 的主体包含了如何创建 ROC 曲线的细节（参见代码清单 3.7）。它执行以下操作：

• 根据神经网络的 S 型输出（概率）的阈值，可获取不同分类结果的集合。

• 将 TPR 绘制在 FPR 上以形成 ROC 曲线。

• ⁸

如 图 3.6 所示，在训练开始时（周期 001），由于模型的权重是随机初始化的，ROC 曲线非常接近连接点 (0, 0) 和点 (1, 1) 的对角线。这就是随机猜测的样子。随着训练的进行，ROC 曲线越来越向左上角推进——那里的 FPR 接近 0，TPR 接近 1。如果我们专注于任何一个给定的 FPR 级别，例如 0.1，我们可以看到在训练过程中，相应的 TPR 值随着训练的进展而单调递增。简而言之，这意味着随着训练的进行，如果我们将假报警率（FPR）保持不变，就可以实现越来越高的召回率（TPR）。

“理想”的 ROC 曲线向左上角弯曲得越多，就会变成一个类似 γ^([8]) 形状的曲线。在这种情况下，您可以获得 100% 的 TPR 和 0% 的 FPR，这是任何二元分类器的“圣杯”。然而，在实际问题中，我们只能改进模型，将 ROC 曲线推向左上角，但理论上的左上角理想状态是无法实现的。

注释：γ 字母

对于每个分类结果，将其与实际标签（目标）结合使用，计算 TPR 和 FPR。

基于对 ROC 曲线形状及其含义的讨论，我们可以看到通过查看其下方的区域（即 ROC 曲线和 x 轴之间的单位正方形的空间）来量化 ROC 曲线的好坏是可能的。这被称为曲线下面积（AUC），并且也在 listing 3.7 的代码中计算。这个指标比精确率、召回率和准确率更好，因为它考虑了假阳性和假阴性之间的权衡。随机猜测的 ROC 曲线（对角线）的 AUC 为 0.5，而γ形状的理想 ROC 曲线的 AUC 为 1.0。我们的钓鱼检测模型在训练后达到了 0.981 的 AUC。

listing 3.7 的代码用于计算和绘制 ROC 曲线和 AUC

function drawROC(targets, probs, epoch) {
  return tf.tidy(() => {
    const thresholds = [                                                ***1***
      0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45,            ***1***
      0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85,                       ***1***
      0.9, 0.92, 0.94, 0.96, 0.98, 1.0                                  ***1***
    ];                                                                  ***1***
    const tprs = [];  // True positive rates.
    const fprs = [];  // False positive rates.
    let area = 0;
    for (let i = 0; i < thresholds.length; ++i) {
           const threshold = thresholds[i];
      const threshPredictions =                                         ***2***
               utils.binarize(probs, threshold).as1D();                 ***2***
      const fpr = falsePositiveRate(                                    ***3***
               targets,                                                 ***3***
      threshPredictions).arraySync();                                   ***3***
      const tpr = tf.metrics.recall(targets, threshPredictions).arraySync();
      fprs.push(fpr);
      tprs.push(tpr);

      if (i > 0) {                                                      ***4***
        area += (tprs[i] + tprs[i - 1]) * (fprs[i - 1] - fprs[i]) / 2;  ***4***
      }                                                                 ***4***
    }
    ui.plotROC(fprs, tprs, epoch);
    return area;
  });
}

• 1 一组手动选择的概率阈值

• 2 通过阈值将概率转换为预测

• 3 falsePositiveRate()函数通过比较预测和实际目标来计算假阳性率。该函数在同一文件中定义。

• 4 用于 AUC 计算的面积累积

除了可视化二元分类器的特性外，ROC 还帮助我们在实际情况下做出明智的选择，比如如何选择概率阈值。例如，想象一下，我们是一家商业公司，正在开发钓鱼检测器作为一项服务。我们想要做以下哪项？

• 由于错过了真实的网络钓鱼网站将会在责任或失去合同方面给我们造成巨大的损失，因此将阈值设定相对较低。

• 由于我们更不愿意接受将正常网站误分类为可疑而导致用户提交投诉，因此将阈值设定相对较高。

每个阈值对应于 ROC 曲线上的一个点。当我们将阈值从 0 逐渐增加到 1 时，我们从图的右上角（其中 FPR 和 TPR 都为 1）移动到图的左下角（其中 FPR 和 TPR 都为 0）。在实际的工程问题中，选择 ROC 曲线上的哪个点的决定总是基于权衡这种相反的现实生活成本，并且在不同的客户和不同的业务发展阶段可能会有所不同。

除了 ROC 曲线之外，二元分类的另一个常用可视化方法是精确率-召回率曲线（有时称为 P/R 曲线，在 table 3.3 中简要提到）。与 ROC 曲线不同，精确率-召回率曲线将精确率绘制为召回率的函数。由于精确率-召回率曲线在概念上与 ROC 曲线相似，我们在这里不会深入讨论它们。

在 代码清单 3.7 中值得指出的一点是使用了 tf.tidy()。这个函数确保了在作为参数传递给它的匿名函数内创建的张量被正确地处理，这样它们就不会继续占用 WebGL 内存。在浏览器中，TensorFlow.js 无法管理用户创建的张量的内存，主要是因为 JavaScript 中缺乏对象终结和底层 TensorFlow.js 张量下层的 WebGL 纹理缺乏垃圾回收。如果这样的中间张量没有被正确清理，就会发生 WebGL 内存泄漏。如果允许这样的内存泄漏持续足够长的时间，最终会导致 WebGL 内存不足错误。附录 B 的 章节 1.3 包含了有关 TensorFlow.js 内存管理的详细教程。此外，附录 B 的 章节 1.5 中还有关于这个主题的练习题。如果您计划通过组合 TensorFlow.js 函数来定义自定义函数，您应该仔细研究这些章节。

3.2.4. 二元交叉熵：二元分类的损失函数

到目前为止，我们已经讨论了几种不同的度量标准，用于量化二元分类器的不同表现方面，比如准确率、精确率和召回率（表 3.3）。但我们还没有讨论一个重要的度量标准，一个可以微分并生成梯度来支持模型梯度下降训练的度量标准。这就是我们在 代码清单 3.5 中简要看到的 binaryCrossentropy，但我们还没有解释过：

model.compile({
  optimizer: 'adam',
  loss: 'binaryCrossentropy',
  metrics: ['accuracy']
});

首先，你可能会问，为什么不能直接以精确度、准确度、召回率，或者甚至 AUC 作为损失函数？毕竟这些指标容易理解。此外，在之前我们见过的回归问题中，我们使用了 MSE 作为训练的损失函数，这是一个相当容易理解的指标。答案是，这些二分类度量指标都无法产生我们需要训练的梯度。以精确度指标为例：要了解为什么它不友好的梯度，请认识到计算精确度需要确定模型的预测哪些是正样本，哪些是负样本（参见 表 3.3 的第一行）。为了做到这一点，必须应用一个 阈值函数，将模型的 sigmoid 输出转换为二进制预测。这里就是问题的关键：虽然阈值函数（在更技术的术语中称为step function）几乎在任何地方都是可微分的（“几乎”是因为它在 0.5 的“跳跃点”处不可微分），但其导数始终恰好为零（参见图 3.7）！如果您试图通过该阈值函数进行反向传播会发生什么呢？因为上游梯度值在某些地方需要与该阈值函数的所有零导数相乘，所以您的梯度最终将全是零。更简单地说，如果将精确度（或准确度、召回率、AUC 等）选为损失，底层阶跃函数的平坦部分使得训练过程无法知道在权重空间中向哪个方向移动可以降低损失值。

图 3.7 用于转换二分类模型的概率输出的阶跃函数，几乎在每个可微点都是可微分的。不幸的是，每个可微分点的梯度（导数）恰好为零。

因此，如果使用精确度作为损失函数，便无法计算有用的梯度，从而阻止了在模型的权重上获得有意义的更新。此限制同样适用于包括准确度、召回率、FPR 和 AUC 在内的度量。虽然这些指标对人类理解二分类器的行为很有用，但对于这些模型的训练过程来说是无用的。

我们针对二分类任务使用的损失函数是二进制交叉熵，它对应于我们的钓鱼检测模型代码中的 'binaryCrossentropy' 配置（见列表 3.5 和 3.6）。算法上，我们可以用以下伪代码来定义二进制交叉熵。

列表 3.8 二进制交叉熵损失函数的伪代码^([9])

⁹

binaryCrossentropy 的实际代码需要防范 prob 或 1 - prob 等恰好为零的情况，否则如果将这些值直接传递给 log 函数，会导致无穷大。这是通过在将它们传递给对数函数之前添加一个非常小的正数（例如 1e-6，通常称为“epsilon”或“修正因子”）来实现的。

function binaryCrossentropy(truthLabel, prob):
  if truthLabel is 1:
        return -log(prob)
  else:
   return -log(1 - prob)

在此伪代码中，truthLabel 是一个数字，取 0 到 1 的值，指示输入样本在现实中是否具有负（0）或正（1）标签。prob 是模型预测的样本属于正类的概率。请注意，与 truthLabel 不同，prob 应为实数，可以取 0 到 1 之间的任何值。log 是自然对数，以 e（2.718）为底，您可能还记得它来自高中数学。binaryCrossentropy 函数的主体包含一个 if-else 逻辑分支，根据 truthLabel 是 0 还是 1 执行不同的计算。图 3.8 在同一图中绘制了这两种情况。

图 3.8。二元交叉熵损失函数。两种情况（truthLabel = 1 和 truthLabel = 0）分别绘制在一起，反映了 代码清单 3.8 中的 if-else 逻辑分支。

在查看 图 3.8 中的图表时，请记住较低的值更好，因为这是一个损失函数。关于损失函数需要注意的重要事项如下：

• 如果 truthLabel 为 1，prob 值接近 1.0 会导致较低的损失函数值。这是有道理的，因为当样本实际上是正例时，我们希望模型输出的概率尽可能接近 1.0。反之亦然：如果 truthLabel 为 0，则当概率值接近 0 时，损失值较低。这也是有道理的，因为在这种情况下，我们希望模型输出的概率尽可能接近 0。

• 与 图 3.7 中显示的二进制阈值函数不同，这些曲线在每个点都有非零斜率，导致非零梯度。这就是为什么它适用于基于反向传播的模型训练。

你可能会问的一个问题是，为什么不重复我们为回归模型所做的事情——只是假装 0-1 值是回归目标，并使用 MSE 作为损失函数？毕竟，MSE 是可微分的，并且计算真实标签和概率之间的 MSE 会产生与binaryCrossentropy一样的非零导数。答案与 MSE 在边界处具有“递减收益”有关。例如，在 表 3.4 中，我们列出了当 truthLabel 为 1 时一些 prob 值的 binaryCrossentropy 和 MSE 损失值。当 prob 接近 1（期望值）时，MSE 相对于binaryCrossentropy的减小速度会越来越慢。因此，当 prob 已经接近 1（例如，0.9）时，它不太好地“鼓励”模型产生较高（接近 1）的 prob 值。同样，当 truthLabel 为 0 时，MSE 也不如 binaryCrossentropy 那样好，不能生成推动模型的 prob 输出向 0 靠近的梯度。

表 3.4. 比较假想的二分类结果的二元交叉熵和 MSE 值

真实标签	概率	二元交叉熵	MSE
1	0.1	2.302	0.81
1	0.5	0.693	0.25
1	0.9	0.100	0.01
1	0.99	0.010	0.0001
1	0.999	0.001	0.000001
1	1	0	0

这展示了二分类问题与回归问题不同的另一个方面：对于二分类问题，损失（binaryCrossentropy）和指标（准确率、精确率等）是不同的，而对于回归问题通常是相同的（例如，meanSquaredError）。正如我们将在下一节看到的那样，多类别分类问题也涉及不同的损失函数和指标。

3.3. 多类别分类

在 第 3.2 节 中，我们探讨了如何构建二分类问题的结构；现在我们将快速进入 非二分类 的处理方式——即，涉及三个或更多类别的分类任务。^([10]) 我们将使用用于说明多类别分类的数据集是 鸢尾花数据集，这是一个有着统计学根源的著名数据集（参见 en.wikipedia.org/wiki/Iris_flower_data_set）。这个数据集关注于三种鸢尾花的品种，分别为 山鸢尾、变色鸢尾 和 维吉尼亚鸢尾。这三种鸢尾花可以根据它们的形状和大小来区分。在 20 世纪初，英国统计学家罗纳德·费舍尔测量了 150 个鸢尾花样本的花瓣和萼片（花的不同部位）的长度和宽度。这个数据集是平衡的：每个目标标签都有确切的 50 个样本。

¹⁰

不要混淆 多类别 分类和 多标签 分类。在多标签分类中，单个输入示例可能对应于多个输出类别。一个例子是检测输入图像中各种类型物体的存在。一个图像可能只包括一个人；另一个图像可能包括一个人、一辆车和一个动物。多标签分类器需要生成一个表示适用于输入示例的所有类别的输出，无论该类别是一个还是多个。本节不涉及多标签分类。相反，我们专注于更简单的单标签、多类别分类，其中每个输入示例都对应于>2 个可能类别中的一个输出类别。

在这个问题中，我们的模型以四个数值特征（花瓣长度、花瓣宽度、萼片长度和萼片宽度）作为输入，并尝试预测一个目标标签（三种物种之一）。该示例位于 tfjs-examples 的 iris 文件夹中，您可以使用以下命令查看并运行：

git clone https://github.com/tensorflow/tfjs-examples.git
cd tfjs-examples/iris
yarn && yarn watch

3.3.1. 对分类数据进行 one-hot 编码

在研究解决鸢尾花分类问题的模型之前，我们需要强调这个多类别分类任务中分类目标（物种）的表示方式。到目前为止，在本书中我们看到的所有机器学习示例都涉及更简单的目标表示，例如下载时间预测问题中的单个数字以及波士顿房屋问题中的数字，以及钓鱼检测问题中的二进制目标的 0-1 表示。然而，在鸢尾问题中，三种花的物种以稍微不那么熟悉的方式称为 one-hot 编码 进行表示。打开 data.js，您将注意到这一行：

const ys = tf.oneHot(tf.tensor1d(shuffledTargets).toInt(), IRIS_NUM_CLASSES);

这里，shuffledTargets 是一个普通的 JavaScript 数组，其中包含按随机顺序排列的示例的整数标签。其元素的值均为 0、1 和 2，反映了数据集中的三种鸢尾花品种。通过调用 tf.tensor1d(shuffledTargets).toInt()，它被转换为 int32 类型的 1D 张量。然后将结果的 1D 张量传递到 tf.oneHot() 函数中，该函数返回形状为 [numExamples, IRIS_NUM_CLASSES] 的 2D 张量。numExamples 是 targets 包含的示例数，而 IRIS_NUM_CLASSES 简单地是常量 3。您可以通过在先前引用的行下面添加一些打印行来查看 targets 和 ys 的实际值，例如：

const ys = tf.oneHot(tf.tensor1d(shuffledTargets).toInt(), IRIS_NUM_CLASSES);
// Added lines for printing the values of `targets` and `ys`.
console.log('Value of targets:', targets);
ys.print();[11]

¹¹

与 targets 不同，ys 不是一个普通的 JavaScript 数组。相反，它是由 GPU 内存支持的张量对象。因此，常规的 console.log 不会显示其值。print() 方法是专门用于从 GPU 中检索值，以形状感知和人性化的方式进行格式化，并将其记录到控制台的方法。

一旦您进行了这些更改，Yarn watch 命令在终端启动的包捆绑器进程将自动重建 Web 文件。然后，您可以打开用于观看此演示的浏览器选项卡中的开发工具，并刷新页面。console.log() 和 print() 调用的打印消息将记录在开发工具的控制台中。您将看到的打印消息将类似于这样：

Value of targets: (50) [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
     0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
     0, 0, 0, 0, 0, 0, 0, 0]

Tensor
    [[1, 0, 0],
     [1, 0, 0],
     [1, 0, 0],
     ...,
     [1, 0, 0],
     [1, 0, 0],
     [1, 0, 0]]

或者

Value of targets: (50) [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
     1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
     1, 1, 1, 1, 1, 1, 1, 1]

Tensor
    [[0, 1, 0],
     [0, 1, 0],
     [0, 1, 0],
     ...,
     [0, 1, 0],
     [0, 1, 0],
     [0, 1, 0]]

等等。用言语来描述，以整数标签 0 为例，您会得到一个值为 [1, 0, 0] 的值行；对于整数标签为 1 的示例，您会得到一个值为 [0, 1, 0] 的行，依此类推。这是独热编码的一个简单明了的例子：它将一个整数标签转换为一个向量，该向量除了在对应标签的索引处的值为 1 之外，其余都为零。向量的长度等于所有可能类别的数量。向量中只有一个 1 值的事实正是这种编码方案被称为“独热”的原因。

对于您来说，这种编码可能看起来过于复杂了。在一个类别中使用三个数字来表示，为什么不使用一个单一的数字就能完成任务呢？为什么我们选择这种复杂的编码而不是更简单和更经济的单整数索引编码呢？这可以从两个不同的角度来理解。

首先，对于神经网络来说，输出连续的浮点型值要比整数值容易得多。在浮点型输出上应用舍入也不够优雅。一个更加优雅和自然的方法是，神经网络的最后一层输出几个单独的浮点型数值，每个数值通过一个类似于我们用于二元分类的 S 型激活函数的精心选择的激活函数被限制在 [0, 1] 区间内。在这种方法中，每个数字都是模型对输入示例属于相应类别的概率的估计。这正是独热编码的用途：它是概率分数的“正确答案”，模型应该通过其训练过程来拟合。

第二，通过将类别编码为整数，我们隐含地为类别创建了一个顺序。例如，我们可以将 鸢尾花 setosa 标记为 0，鸢尾花 versicolor 标记为 1，鸢尾花 virginica 标记为 2。但是，这样的编号方案通常是人为的和不合理的。例如，这种编号方案暗示 setosa 比 versicolor 更“接近” virginica，这可能并不正确。神经网络基于实数进行操作，并且基于诸如乘法和加法之类的数学运算。因此，它们对数字的数量和顺序敏感。如果将类别编码为单一数字，则成为神经网络必须学习的额外非线性关系。相比之下，独热编码的类别不涉及任何隐含的排序，因此不会以这种方式限制神经网络的学习能力。

就像我们将在第九章中看到的那样，独热编码不仅用于神经网络的输出目标，而且还适用于分类数据形成神经网络的输入。

3.3.2. Softmax 激活函数

了解了输入特征和输出目标的表示方式后，我们现在可以查看定义模型的代码（来自 iris/index.js）。

列表 3.9. 用于鸢尾花分类的多层神经网络

  const model = tf.sequential();
  model.add(tf.layers.dense(
      {units: 10, activation: 'sigmoid', inputShape: [xTrain.shape[1]]}));
  model.add(tf.layers.dense({units: 3, activation: 'softmax'}));
  model.summary();

  const optimizer = tf.train.adam(params.learningRate);
  model.compile({
    optimizer: optimizer,
    loss: 'categoricalCrossentropy',
    metrics: ['accuracy'],
  });

在列表 3.9 中定义的模型导致了以下摘要：

_________________________________________________________________
Layer (type)                 Output shape              Param #
=================================================================
dense_Dense1 (Dense)         [null,10]                 50
________________________________________________________________
dense_Dense2 (Dense)         [null,3]                  33
=================================================================
Total params: 83
Trainable params: 83
Non-trainable params:
________________________________________________________________

通过查看打印的概述，我们可以看出这是一个相当简单的模型，具有相对较少的（83 个）权重参数。输出形状[null, 3]对应于分类目标的独热编码。最后一层使用的激活函数，即softmax，专门设计用于多分类问题。softmax 的数学定义可以写成以下伪代码：

softmax([x1, x2, ..., xn]) =
    [exp(x1) / (exp(x1) + exp(x2) + ... + exp(xn)),
     exp(x2) / (exp(x1) + exp(x2) + ... + exp(xn)),
     ...,
     exp(xn) / (exp(x1) + exp(x2) + ... + exp(xn))]

与我们之前见过的 sigmoid 激活函数不同，softmax 激活函数不是逐元素的，因为输入向量的每个元素都以依赖于所有其他元素的方式进行转换。具体来说，输入的每个元素被转换为其指数（以* e*=2.718 为底）的自然指数。然后指数被除以所有元素的指数的和。这样做有什么作用？首先，它确保了每个数字都在 0 到 1 的区间内。其次，保证了输出向量的所有元素之和为 1。这是一个理想的属性，因为 1）输出可以被解释为分配给各个类别的概率得分，2）为了与分类交叉熵损失函数兼容，输出必须满足此属性。第三，该定义确保输入向量中的较大元素映射到输出向量中的较大元素。举个具体的例子，假设最后一个密集层的矩阵乘法和偏置相加生成了一个向量

[-3, 0, -8]

它的长度为 3，因为密集层被配置为具有 3 个单元。请注意，这些元素是浮点数，不受特定范围的约束。softmax 激活函数将向量转换为

[0.0474107, 0.9522698, 0.0003195]

您可以通过运行以下 TensorFlow.js 代码（例如，在页面指向js.tensorflow.org时，在开发工具控制台中）来自行验证这一点：

const x = tf.tensor1d([-3, 0, -8]);
tf.softmax(x).print();

Softmax 函数的输出有三个元素。1）它们都在[0, 1]区间内，2）它们的和为 1，3）它们的顺序与输入向量中的顺序相匹配。由于这些属性的存在，输出可以被解释为被模型分配的（概率）值，表示所有可能的类别。在前面的代码片段中，第二个类别被分配了最高的概率，而第一个类别被分配了最低的概率。

因此，当使用这种多类别分类器的输出时，你可以选择最高 softmax 元素的索引作为最终决策——也就是输入属于哪个类别的决策。这可以通过使用方法 argMax() 来实现。例如，这是 index.js 的摘录：

const predictOut = model.predict(input);
const winner = data.IRIS_CLASSES[predictOut.argMax(-1).dataSync()[0]];

predictOut 是形状为 [numExamples, 3] 的二维张量。调用它的 argMax0 方法会导致形状被减少为 [numExample]。参数值 -1 表示 argMax() 应该在最后一个维度上查找最大值并返回它们的索引。例如，假设 predictOut 有以下值：

    [[0  , 0.6, 0.4],
     [0.8, 0  , 0.2]]

那么，argMax(-1) 将返回一个张量，指示沿着最后（第二个）维度找到的最大值分别在第一个和第二个示例的索引为 1 和 0：

    [1, 0]

3.3.3. 分类交叉熵：多类别分类的损失函数

在二元分类示例中，我们看到了如何使用二元交叉熵作为损失函数，以及为什么其他更易于人类理解的指标，如准确率和召回率，不能用作损失函数。多类别分类的情况相当类似。存在一个直观的度量标准——准确率——它是模型正确分类的例子的比例。这个指标对于人们理解模型的性能有重要意义，并且在 列表 3.9 中的这段代码片段中使用：

    model.compile({
      optimizer: optimizer,
      loss: 'categoricalCrossentropy',
      metrics: ['accuracy'],
     });

然而，准确率对于损失函数来说是一个糟糕的选择，因为它遇到了与二元分类中的准确率相同的零梯度问题。因此，人们为多类别分类设计了一个特殊的损失函数：分类交叉熵。它只是将二元交叉熵推广到存在两个以上类别的情况。

列表 3.10. 用于分类交叉熵损失的伪代码

function categoricalCrossentropy(oneHotTruth, probs):
  for i in (0 to length of oneHotTruth)
    if oneHotTruth(i) is equal to 1
      return -log(probs[i]);

在前面的伪代码中，oneHotTruth 是输入示例的实际类别的独热编码。probs 是模型的 softmax 概率输出。从这段伪代码中可以得出的关键信息是，就分类交叉熵而言，probs 中只有一个元素是重要的，那就是与实际类别对应的索引的元素。probs 的其他元素可以随意变化，但只要它们不改变实际类别的元素，就不会影响分类交叉熵。对于 probs 的特定元素，它越接近 1，交叉熵的值就越低。与二元交叉熵类似，分类交叉熵直接作为 tf.metrics 命名空间下的一个函数可用，你可以用它来计算简单但说明性的示例的分类交叉熵。例如，使用以下代码，你可以创建一个假设的独热编码的真实标签和一个假设的 probs 向量，并计算相应的分类交叉熵值：

const oneHotTruth = tf.tensor1d([0, 1, 0]);
const probs = tf.tensor1d([0.2, 0.5, 0.3]);
tf.metrics.categoricalCrossentropy(oneHotTruth, probs).print();

这给出了一个约为 0.693 的答案。这意味着当模型对实际类别分配的概率为 0.5 时，categoricalCrossentropy的值为 0.693。你可以根据 pseudo-code(伪代码)进行验证。你也可以尝试将值从 0.5 提高或降低，看看categoricalCrossentropy如何变化（例如，参见 table 3.5）。表中还包括一列显示了单热真实标签和probs向量之间的 MSE。

表 3.5. 不同概率输出下的分类交叉熵值。不失一般性，所有示例（行）都是基于有三个类别的情况（如鸢尾花数据集），并且实际类别是第二个类别。

One-hot truth label	probs (softmax output)	Categorical cross entropy	MSE
[0, 1, 0]	[0.2, 0.5, 0.3]	0.693	0.127
[0, 1, 0]	[0.0, 0.5, 0.5]	0.693	0.167
[0, 1, 0]	[0.0, 0.9, 0.1]	0.105	0.006
[0, 1, 0]	[0.1, 0.9, 0.0]	0.105	0.006
[0, 1, 0]	[0.0, 0.99, 0.01]	0.010	0.00006

通过比较表中的第 1 行和第 2 行，或比较第 3 行和第 4 行，可以明显看出更改probs中与实际类别不对应的元素不会改变二元交叉熵的值，尽管这可能会改变单热真实标签和probs之间的 MSE。同样，就像在二元交叉熵中一样，当probs值接近 1 时，MSE 显示出递减的回报，并且在这个区间内，MSE 不适合鼓励正确类别的概率值上升，而分类熵则更适合作为多类别分类问题的损失函数。

3.3.4. 混淆矩阵：多类别分类的细致分析

点击示例网页上的从头开始训练模型按钮，你可以在几秒钟内得到一个经过训练的模型。正如图 3.9 所示，模型经过 40 个训练周期后几乎达到了完美的准确度。这反映了鸢尾花数据集是一个相对较小且在特征空间中类别边界相对明确的数据集的事实。

图 3.9. 40 个训练周期后鸢尾花模型的典型结果。左上方：损失函数随训练周期变化的图表。右上方：准确度随训练周期变化的图表。底部：混淆矩阵。

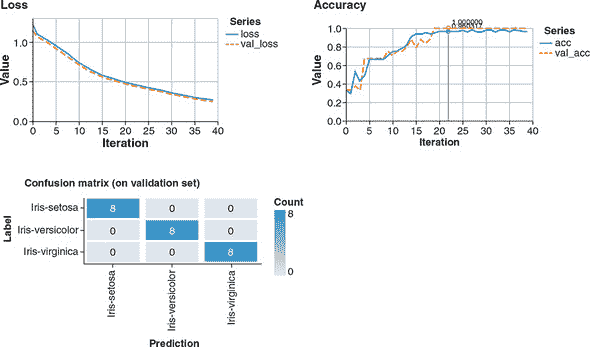
图 3.9 的底部显示了描述多类分类器行为的另一种方式，称为混淆矩阵。混淆矩阵根据其实际类别和模型预测类别将多类分类器的结果进行了细分。它是一个形状为[numClasses, numClasses]的方阵。索引[i, j]（第 i 行和第 j 列）处的元素是属于类别i并由模型预测为类别j的示例数量。因此，混淆矩阵的对角线元素对应于正确分类的示例。一个完美的多类分类器应该产生一个没有对角线之外的非零元素的混淆矩阵。这正是图 3.9 中的混淆矩阵的情况。

除了展示最终的混淆矩阵外，鸢尾花示例还在每个训练周期结束时使用onTrainEnd()回调绘制混淆矩阵。在早期周期中，您可能会看到一个不太完美的混淆矩阵，与图 3.9 中的混淆矩阵不同。图 3.10 中的混淆矩阵显示，24 个输入示例中有 8 个被错误分类，对应的准确率为 66.7%。然而，混淆矩阵告诉我们不仅仅是一个数字：它显示了哪些类别涉及最多的错误，哪些涉及较少。在这个特定的示例中，所有来自第二类的花都被错误分类（要么作为第一类，要么作为第三类），而来自第一类和第三类的花总是被正确分类。因此，您可以看到，在多类分类中，混淆矩阵比简单的准确率更具信息量，就像精确率和召回率一起形成了比二分类准确率更全面的衡量标准一样。混淆矩阵可以提供有助于与模型和训练过程相关的决策的信息。例如，某些类型的错误可能比混淆其他类别对更为昂贵。也许将一个体育网站误认为游戏网站不如将体育网站误认为钓鱼网站那么严重。在这些情况下，您可以调整模型的超参数以最小化最昂贵的错误。

图 3.10. 一个“不完美”混淆矩阵的示例，在对角线之外存在非零元素。该混淆矩阵是在训练收敛之前的仅 2 个周期后生成的。

到目前为止，我们所见的模型都将一组数字作为输入。换句话说，每个输入示例都表示为一组简单的数字列表，其中长度固定，元素的排序不重要，只要它们对馈送到模型的所有示例都一致即可。虽然这种类型的模型涵盖了重要和实用的机器学习问题的大量子集，但它远非唯一的类型。在接下来的章节中，我们将研究更复杂的输入数据类型，包括图像和序列。在 第四章 中，我们将从图像开始，这是一种无处不在且广泛有用的输入数据类型，为此已经开发了强大的神经网络结构，以将机器学习模型的准确性推向超人级别。

练习

1. 当创建用于波士顿房屋问题的神经网络时，我们停留在一个具有两个隐藏层的模型上。鉴于我们所说的级联非线性函数会增强模型的容量，那么将更多的隐藏层添加到模型中会导致评估准确性提高吗？通过修改 index.js 并重新运行训练和评估来尝试一下。

   1. 是什么因素阻止了更多的隐藏层提高评估准确性？

   2. 是什么让您得出这个结论？（提示：看一下训练集上的误差。）

2. 看看 清单 3.6 中的代码如何使用 onEpochBegin 回调在每个训练时期的开始计算并绘制 ROC 曲线。您能按照这种模式并对回调函数的主体进行一些修改，以便您可以在每个时期的开始打印精度和召回率值（在测试集上计算）吗？描述这些值随着训练的进行而如何变化。

3. 研究 清单 3.7 中的代码，并理解它是如何计算 ROC 曲线的。您能按照这个示例并编写一个新的函数，名为 drawPrecisionRecallCurve()，它根据名称显示一个精度-召回率曲线吗？写完函数后，从 onEpochBegin 回调中调用它，以便在每个训练时期的开始绘制一个精度-召回率曲线。您可能需要对 ui.js 进行一些修改或添加。

4. 假设您得知二元分类器结果的 FPR 和 TPR。凭借这两个数字，您能计算出整体准确性吗？如果不能，您需要什么额外信息？

5. 二元交叉熵（3.2.4 节）和分类交叉熵（3.3.3 节）的定义都基于自然对数（以 e 为底的对数）。如果我们改变定义，让它们使用以 10 为底的对数会怎样？这会如何影响二元和多类分类器的训练和推断？

6. 将超参数网格搜索的伪代码转换为实际的 JavaScript 代码，并使用该代码对列表 3.1 中的两层波士顿房屋模型进行超参数优化。具体来说，调整隐藏层的单位数和学习率。可以自行决定要搜索的单位和学习率的范围。注意，机器学习工程师通常使用近似几何序列（即对数）间隔进行这些搜索（例如，单位= 2、5、10、20、50、100、200，…）。

摘要

• 分类任务与回归任务不同，因为它们涉及进行离散预测。

• 分类有两种类型：二元和多类。在二元分类中，对于给定的输入，有两种可能的类别，而在多类分类中，有三个或更多。

• 二元分类通常可以被看作是在所有输入示例中检测一种称为正例的特定类型事件或对象。从这个角度来看，我们可以使用精确率、召回率和 FPR 等指标，除了准确度，来量化二元分类器行为的各个方面。

• 在二元分类任务中，需要在捕获所有正例和最小化假阳性（误报警）之间进行权衡是很常见的。ROC 曲线与相关的 AUC 指标是一种帮助我们量化和可视化这种关系的技术。

• 为了进行二元分类而创建的神经网络应该在其最后（输出）层使用 sigmoid 激活，并在训练过程中使用二元交叉熵作为损失函数。

• 为了创建一个用于多类分类的神经网络，输出目标通常由独热编码表示。神经网络应该在其输出层使用 softmax 激活，并使用分类交叉熵损失函数进行训练。

• 对于多类分类，混淆矩阵可以提供比准确度更细粒度的信息，关于模型所犯错误的信息。

• 表 3.6 总结了迄今为止我们见过的最常见的机器学习问题类型（回归、二元分类和多类分类）的推荐方法。

• 超参数是关于机器学习模型结构、其层属性以及其训练过程的配置。它们与模型的权重参数不同，因为 1）它们在模型的训练过程中不变化，2）它们通常是离散的。超参数优化是一种寻找超参数值以在验证数据集上最小化损失的过程。超参数优化仍然是一个活跃的研究领域。目前，最常用的方法包括网格搜索、随机搜索和贝叶斯方法。

表格 3.6. 最常见的机器学习任务类型，它们适用的最后一层激活函数和损失函数，以及有助于量化模型质量的指标的概述

任务类型	输出层的激活函数	损失函数	在 Model.fit() 调用中支持的适用指标	额外的指标
回归	‘linear’ (默认)	‘meanSquaredError’ 或 ‘meanAbsoluteError’	(与损失函数相同)
二分类	‘sigmoid’	‘binaryCrossentropy’	‘accuracy’	精确率，召回率，精确-召回曲线，ROC 曲线，AUC 值
单标签，多类别分类	‘softmax’	‘categoricalCrossentropy’	‘accuracy’	混淆矩阵

---

1. 7 ↩︎