如何开发预测车险赔付的神经网络
原文:https://machinelearningmastery.com/predicting-car-insurance-payout/
为新数据集开发神经网络预测模型可能具有挑战性。
一种方法是首先检查数据集,并为哪些模型可能起作用提出想法,然后探索数据集上简单模型的学习动态,最后利用强大的测试工具为数据集开发和调整模型。
该过程可用于开发用于分类和回归预测建模问题的有效神经网络模型。
在本教程中,您将发现如何为瑞典汽车保险回归数据集开发多层感知机神经网络模型。
完成本教程后,您将知道:
- 如何加载和总结瑞典汽车保险数据集,并使用结果建议数据准备和模型配置使用。
- 如何探索数据集上简单 MLP 模型和数据转换的学习动态。
- 如何对模型表现进行稳健估计,调整模型表现,并对新数据进行预测。
我们开始吧。

如何开发预测车险赔付的神经网络
图片由迪米特里·b .提供,版权所有。
教程概述
本教程分为四个部分;它们是:
- 汽车保险回归数据集
- 第一 MLP 和学习动力
- 评估和调整 MLP 模型
- 最终模型和做出预测
汽车保险回归数据集
第一步是定义和探索数据集。
我们将使用“汽车保险”标准回归数据集。
数据集描述了瑞典汽车保险。有一个单一的输入变量,即索赔数量,目标变量是以千瑞典克朗为单位的索赔付款总额。目标是预测给定索赔数量的总付款。
您可以在此了解有关数据集的更多信息:
您可以在下面看到数据集的前几行。
108,392.5
19,46.2
13,15.7
124,422.2
40,119.4
...
我们可以看到这些值是数字,可能从几十到几百。这表明当用神经网络建模时,某种类型的缩放将适用于数据。
我们可以直接从网址将数据集加载为熊猫数据帧;例如:
# load the dataset and summarize the shape
from pandas import read_csv
# define the location of the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
# load the dataset
df = read_csv(url, header=None)
# summarize shape
print(df.shape)
运行该示例直接从 URL 加载数据集,并报告数据集的形状。
在这种情况下,我们可以确认数据集有两个变量(一个输入和一个输出),并且数据集有 63 行数据。
对于一个神经网络来说,这不是很多行的数据,这表明一个小的网络,也许有正则化,将是合适的。
它还建议使用 k 倍交叉验证将是一个好主意,因为它将给出比训练/测试分割更可靠的模型表现估计,并且因为单个模型将在几秒钟内适合最大数据集,而不是几小时或几天。
(63, 2)
接下来,我们可以通过查看汇总统计数据和数据图来了解更多关于数据集的信息。
# show summary statistics and plots of the dataset
from pandas import read_csv
from matplotlib import pyplot
# define the location of the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
# load the dataset
df = read_csv(url, header=None)
# show summary statistics
print(df.describe())
# plot histograms
df.hist()
pyplot.show()
运行该示例首先加载之前的数据,然后打印每个变量的汇总统计信息
我们可以看到,每个变量的平均值都在十位数,取值范围从 0 到数百。这证实了扩展数据可能是一个好主意。
0 1
count 63.000000 63.000000
mean 22.904762 98.187302
std 23.351946 87.327553
min 0.000000 0.000000
25% 7.500000 38.850000
50% 14.000000 73.400000
75% 29.000000 140.000000
max 124.000000 422.200000
然后为每个变量创建直方图。
我们可以看到每个变量都有相似的分布。它看起来像一个偏斜的高斯分布或指数分布。
我们在每个变量上使用幂变换可能会有一些好处,以便使概率分布不那么偏斜,这可能会提高模型表现。
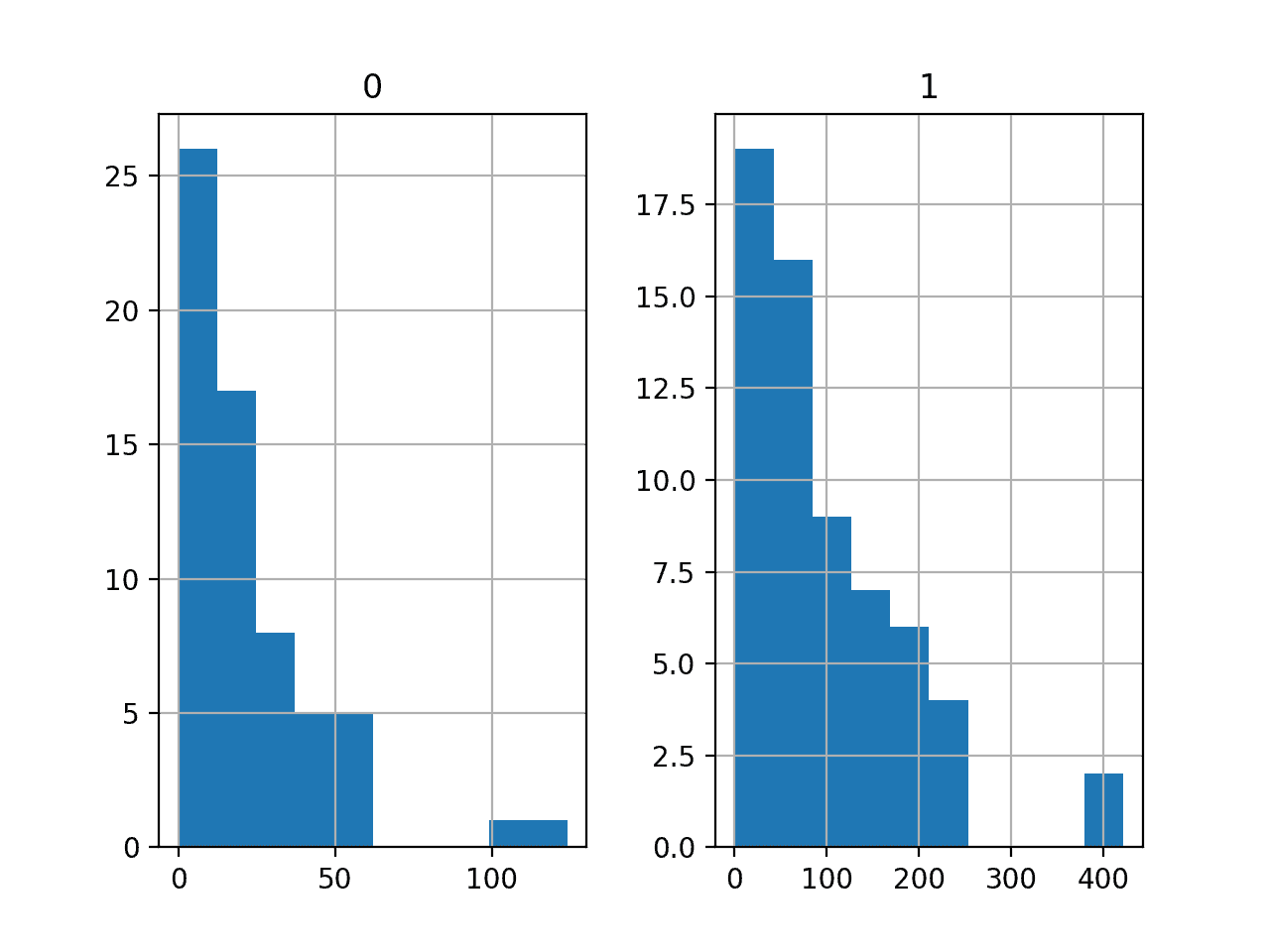
汽车保险回归数据集的直方图
现在我们已经熟悉了数据集,让我们探索如何开发一个神经网络模型。
第一 MLP 和学习动力
我们将使用张量流为数据集开发一个多层感知机(MLP)模型。
我们无法知道什么样的学习超参数的模型架构对这个数据集是好的或最好的,所以我们必须实验并发现什么是好的。
假设数据集很小,小的批量可能是个好主意,例如 8 或 16 行。开始时使用亚当版本的随机梯度下降是一个好主意,因为它会自动调整学习速率,并且在大多数数据集上运行良好。
在我们认真评估模型之前,最好回顾学习动态,调整模型架构和学习配置,直到我们有稳定的学习动态,然后看看如何从模型中获得最大收益。
我们可以通过对数据进行简单的训练/测试分割并查看学习曲线的曲线来做到这一点。这将有助于我们了解自己是学习过度还是学习不足;然后我们可以相应地调整配置。
首先,我们可以将数据集拆分成输入和输出变量,然后分成 67/33 训练和测试集。
...
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
接下来,我们可以定义一个最小 MLP 模型。在这种情况下,我们将使用一个具有 10 个节点的隐藏层和一个输出层(任意选择)。我们将使用隐藏层中的 ReLU 激活函数和 he_normal 权重初始化,作为一个整体,它们是一个很好的实践。
模型的输出是线性激活(无激活),我们将最小化均方误差(MSE)损失。
...
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
我们将为 100 个训练时期(任意选择)拟合模型,批次大小为 8,因为它是一个小数据集。
我们正在原始数据上拟合模型,我们认为这可能是一个坏主意,但这是一个重要的起点。
...
# fit the model
history = model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0, validation_data=(X_test,y_test))
在训练结束时,我们将评估模型在测试数据集上的表现,并将表现报告为平均绝对误差(MAE),与 MSE 或 r MSE 相比,我通常更喜欢它。
...
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % score)
最后,我们将绘制训练和测试集上的均方误差损失的学习曲线。
...
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
将所有这些结合起来,下面列出了在汽车保险数据集上评估我们的第一个 MLP 的完整示例。
# fit a simple mlp model and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
运行该示例首先在训练数据集上拟合模型,然后在测试数据集上报告 MAE。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到模型实现了大约 33.2 的 MAE,这是一个很好的表现基线,我们可能可以在此基础上进行改进。
MAE: 33.233
然后创建列车和测试集上的最小均方误差线图。
我们可以看到,该模型具有很好的拟合性和很好的收敛性。模型的配置是一个很好的起点。
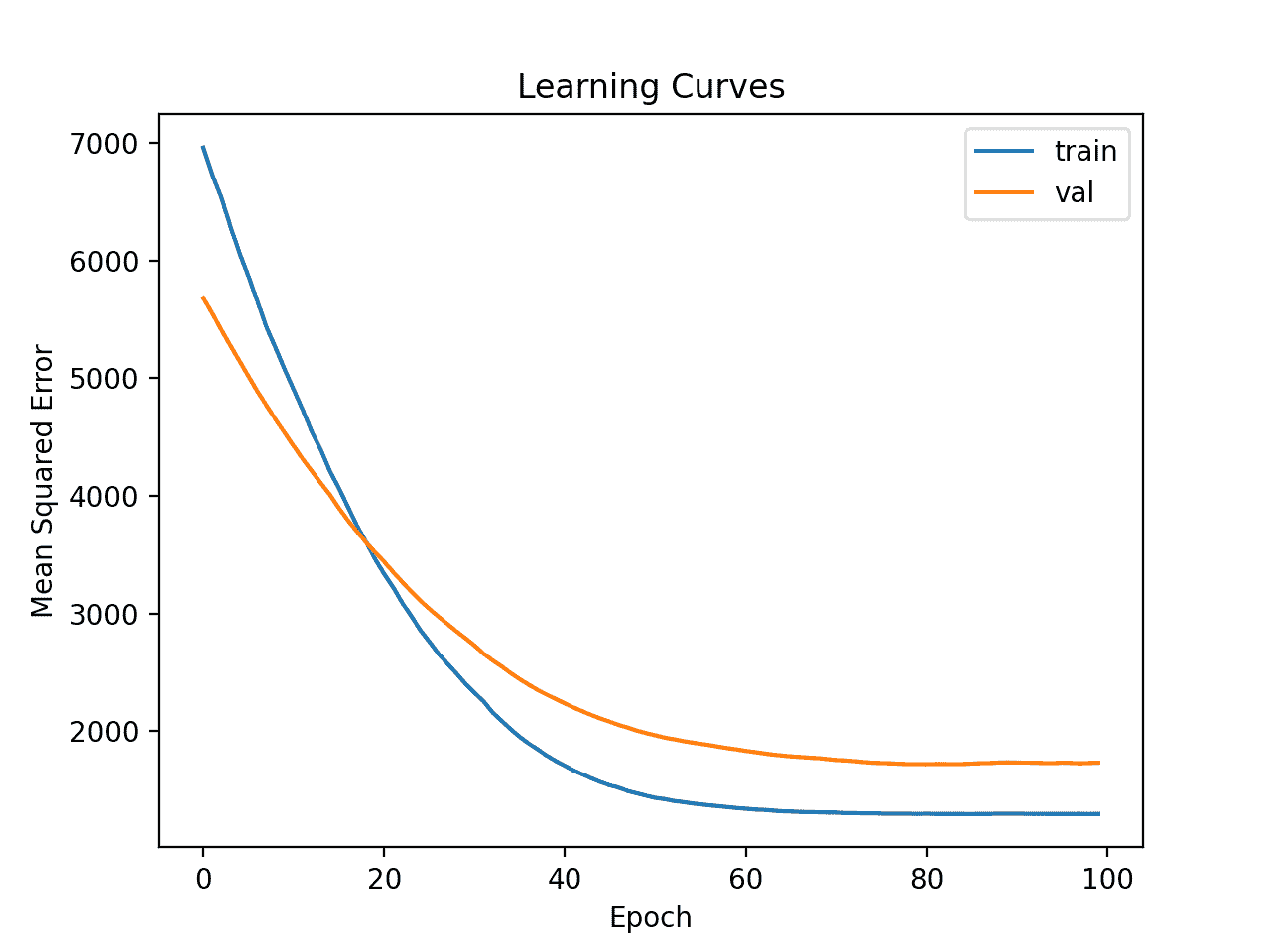
简单 MLP 在汽车保险数据集上的学习曲线
到目前为止,学习动态是好的,MAE 是一个粗略的估计,不应该依赖。
我们可能会稍微增加模型的容量,并期望类似的学习动态。例如,我们可以添加第二个具有八个节点的隐藏层(任意选择),并将训练时期的数量增加一倍至 200。
...
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0, validation_data=(X_test,y_test))
下面列出了完整的示例。
# fit a deeper mlp model and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
运行该示例首先在训练数据集上拟合模型,然后在测试数据集上报告 MAE。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到 MAE 略有提高,约为 27.9,尽管列车/测试分割的高方差意味着这种评估不可靠。
MAE: 27.939
然后绘制最小均方误差训练和测试集的学习曲线。我们可以看到,正如预期的那样,模型在合理的迭代次数内实现了良好的拟合和收敛。
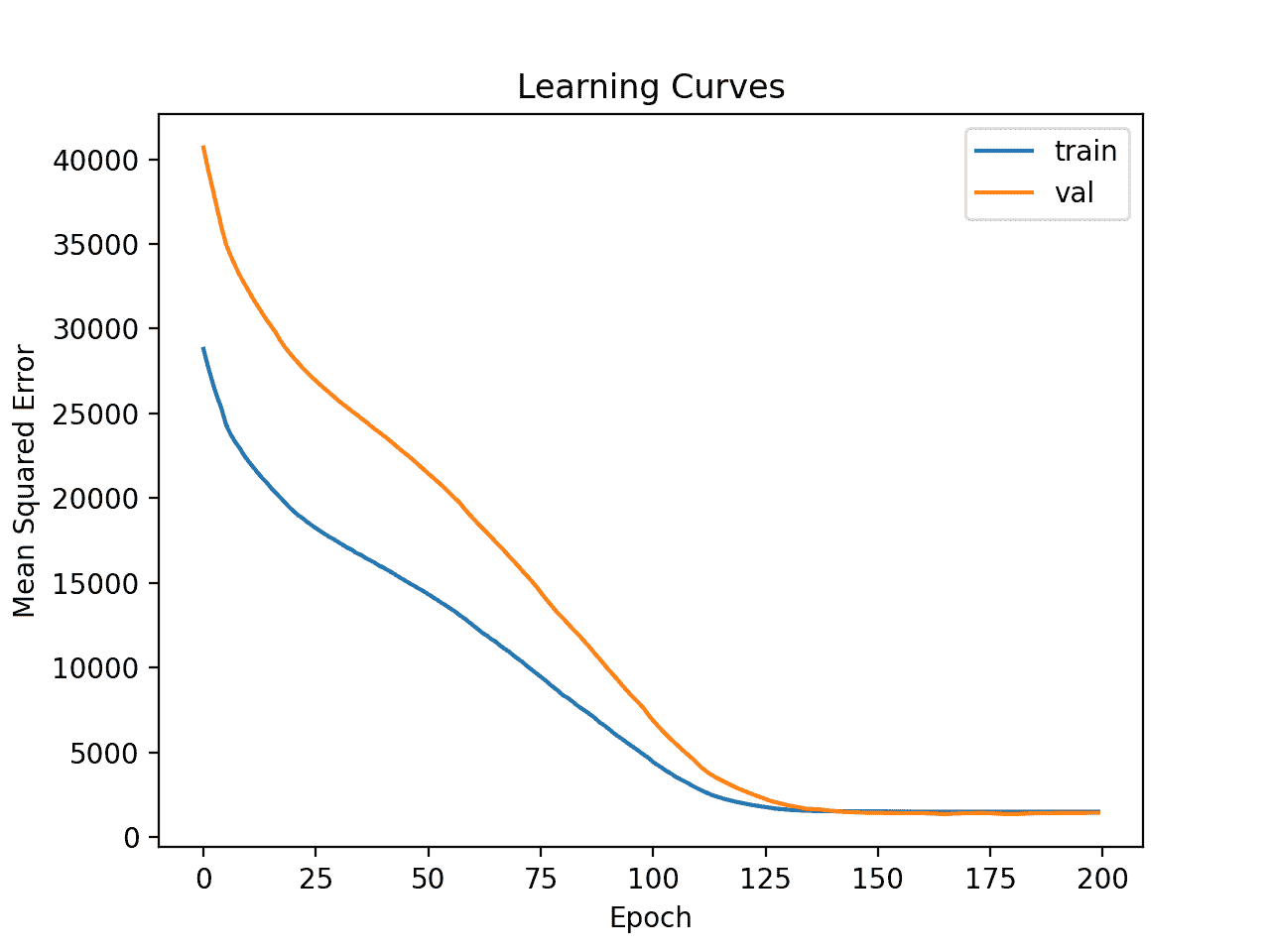
汽车保险数据集上的深 MLP 学习曲线
最后,我们可以尝试转换数据,看看这会如何影响学习动态。
在这种情况下,我们将使用幂变换来减少数据分布的偏差。这也将自动标准化变量,使它们的平均值为零,标准偏差为 1——这是用神经网络建模时的一个良好做法。
首先,我们必须确保目标变量是一个二维数组。
...
# ensure that the target variable is a 2d array
y_train, y_test = y_train.reshape((len(y_train),1)), y_test.reshape((len(y_test),1))
接下来,我们可以将电力变压器应用于输入和目标变量。
这可以通过首先在训练数据上拟合变换,然后变换训练集和测试集来实现。
该过程对输入和输出变量分别应用于以避免数据泄露。
...
# power transform input data
pt1 = PowerTransformer()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# power transform output data
pt2 = PowerTransformer()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
数据然后被用于拟合模型。
然后,可以根据模型做出的预测和测试集的预期目标值对转换进行反演,我们可以像以前一样以正确的比例计算 MAE。
...
# inverse transforms on target variable
y_test = pt2.inverse_transform(y_test)
yhat = pt2.inverse_transform(yhat)
将这些联系在一起,下面列出了用转换后的数据拟合和评估 MLP 并创建模型的学习曲线的完整示例。
# fit a mlp model with data transforms and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import PowerTransformer
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# ensure that the target variable is a 2d array
y_train, y_test = y_train.reshape((len(y_train),1)), y_test.reshape((len(y_test),1))
# power transform input data
pt1 = PowerTransformer()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# power transform output data
pt2 = PowerTransformer()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict(X_test)
# inverse transforms on target variable
y_test = pt2.inverse_transform(y_test)
yhat = pt2.inverse_transform(yhat)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
运行该示例首先在训练数据集上拟合模型,然后在测试数据集上报告 MAE。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,该模型获得了合理的 MAE 分数,尽管比以前报告的表现差。我们将暂时忽略模型表现。
MAE: 34.320
创建的学习曲线的线图表明,该模型实现了合理的拟合,并且有足够的时间收敛。
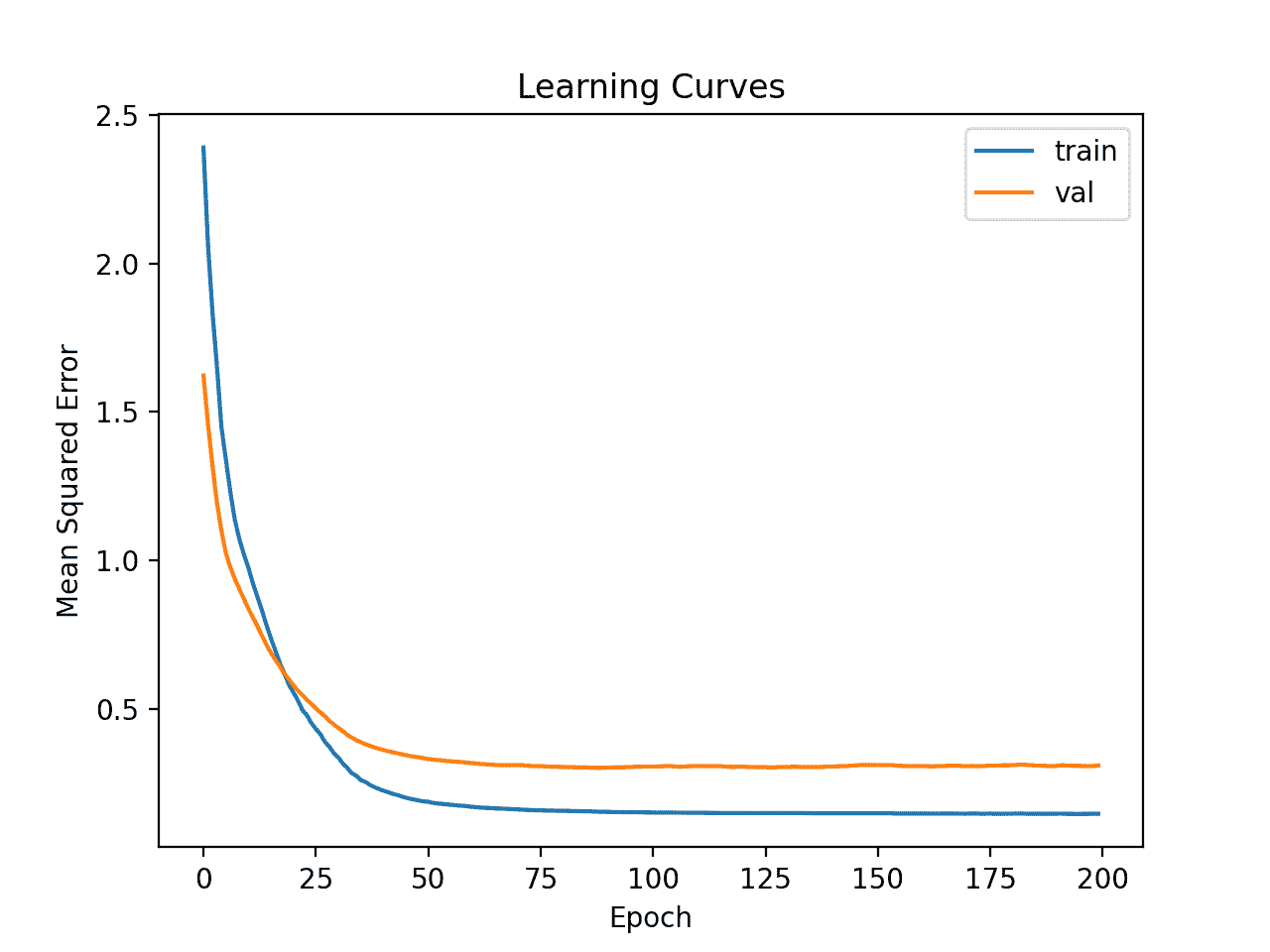
利用汽车保险数据集上的数据变换学习深度 MLP 曲线
现在,我们已经对简单 MLP 模型的学习动态有了一些了解,无论有没有数据转换,我们都可以评估模型的表现以及调整模型的配置。
评估和调整 MLP 模型
k 倍交叉验证程序可以提供更可靠的 MLP 表现估计,尽管它可能非常慢。
这是因为 k 模型必须拟合和评估。当数据集很小时,例如汽车保险数据集,这不是问题。
我们可以使用 KFold 类创建拆分并手动枚举每个折叠,拟合模型,对其进行评估,然后在过程结束时报告评估分数的平均值。
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# fit and evaluate the model...
...
...
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
我们可以使用这个框架,通过一系列不同的数据准备、模型架构和学习配置,来开发 MLP 模型表现的可靠估计。
重要的是,在使用 k-fold 交叉验证来估计表现之前,我们首先了解了上一节中模型在数据集上的学习动态。如果我们开始直接调整模型,我们可能会得到好的结果,但如果没有,我们可能不知道为什么,例如,模型过度或拟合不足。
如果我们再次对模型进行大的更改,最好返回并确认模型正在适当收敛。
下面列出了评估前一节中的基本 MLP 模型的框架的完整示例。
# k-fold cross-validation of base model for the auto insurance regression dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0)
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
运行该示例会报告评估程序每次迭代的模型表现,并在运行结束时报告 MAE 的平均值和标准偏差。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到 MLP 模型实现了大约 38.913 的 MAE。
我们将使用这个结果作为我们的基线,看看我们是否可以实现更好的表现。
>27.314
>69.577
>20.891
>14.810
>13.412
>69.540
>25.612
>49.508
>35.769
>62.696
Mean MAE: 38.913 (21.056)
首先,让我们尝试在原始数据集上评估更深层次的模型,看看它是否比基线模型表现得更好。
...
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0)
下面列出了完整的示例。
# k-fold cross-validation of deeper model for the auto insurance regression dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0)
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
运行报告运行结束时的平均和标准偏差。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到 MLP 模型实现了大约 35.384 的 MAE,这比基线模型实现了大约 38.913 的 MAE 稍好。
Mean MAE: 35.384 (14.951)
接下来,让我们尝试使用与上一节相同的模型,对输入变量和目标变量进行幂变换。
下面列出了完整的示例。
# k-fold cross-validation of deeper model with data transforms
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import PowerTransformer
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# ensure target is a 2d array
y_train, y_test = y_train.reshape((len(y_train),1)), y_test.reshape((len(y_test),1))
# prepare input data
pt1 = PowerTransformer()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# prepare target
pt2 = PowerTransformer()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0)
# predict test set
yhat = model.predict(X_test)
# inverse transforms
y_test = pt2.inverse_transform(y_test)
yhat = pt2.inverse_transform(yhat)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
运行报告运行结束时的平均和标准偏差。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到 MLP 模型实现了大约 37.371 的 MAE,比基线模型好,但并不比更深的基线模型好。
也许这种转变并不像我们最初认为的那样有帮助。
Mean MAE: 37.371 (29.326)
另一种变换是标准化输入和目标变量。
这意味着将每个变量的值缩放到范围[0,1]。我们可以使用最小最大缩放器来实现这一点;例如:
...
# prepare input data
pt1 = MinMaxScaler()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# prepare target
pt2 = MinMaxScaler()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
将这些联系在一起,下面列出了使用数据规范化评估更深层次的 MLP 的完整示例。
# k-fold cross-validation of deeper model with normalization transforms
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# ensure target is a 2d array
y_train, y_test = y_train.reshape((len(y_train),1)), y_test.reshape((len(y_test),1))
# prepare input data
pt1 = MinMaxScaler()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# prepare target
pt2 = MinMaxScaler()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0)
# predict test set
yhat = model.predict(X_test)
# inverse transforms
y_test = pt2.inverse_transform(y_test)
yhat = pt2.inverse_transform(yhat)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
运行报告运行结束时的平均和标准偏差。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到 MLP 模型实现了大约 30.388 的 MAE,这比我们迄今为止尝试的任何其他配置都要好。
Mean MAE: 30.388 (14.258)
我们可以继续测试模型架构的替代配置(更多或更少的节点或层)、学习超参数(更多或更少的批次)和数据转换。
我把这个作为练习;让我知道你的发现。能不能取得更好的成绩?
在下面的评论中发布你的结果,我很想看看你得到了什么。
接下来,让我们看看如何拟合最终模型并使用它进行预测。
最终模型和做出预测
一旦我们选择了一个模型配置,我们就可以在所有可用的数据上训练一个最终模型,并使用它来对新数据进行预测。
在这种情况下,我们将使用带有数据规范化的深层模型作为最终模型。
这意味着,如果我们想将模型保存到文件中,我们必须保存模型本身(用于进行预测)、输入数据的转换(用于新的输入数据)和目标变量的转换(用于新的预测)。
我们可以像以前一样准备数据并拟合模型,尽管是在整个数据集上,而不是数据集的训练子集上。
...
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure target is a 2d array
y = y.reshape((len(y),1))
# prepare input data
pt1 = MinMaxScaler()
pt1.fit(X)
X = pt1.transform(X)
# prepare target
pt2 = MinMaxScaler()
pt2.fit(y)
y = pt2.transform(y)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
然后,我们可以使用这个模型对新数据进行预测。
首先,我们可以定义一行新数据,这只是这个数据集的一个变量。
...
# define a row of new data
row = [13]
然后,我们可以转换这些新数据,准备用作模型的输入。
...
# transform the input data
X_new = pt1.transform([row])
然后我们可以做一个预测。
...
# make prediction
yhat = model.predict(X_new)
然后反转预测的变换,这样我们就可以用正确的比例来使用或解释结果。
...
# invert transform on prediction
yhat = pt2.inverse_transform(yhat)
在这种情况下,我们将简单地报告预测。
...
# report prediction
print('f(%s) = %.3f' % (row, yhat[0]))
将所有这些结合起来,下面列出了为汽车保险数据集拟合最终模型并使用它对新数据进行预测的完整示例。
# fit a final model and make predictions on new data.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure target is a 2d array
y = y.reshape((len(y),1))
# prepare input data
pt1 = MinMaxScaler()
pt1.fit(X)
X = pt1.transform(X)
# prepare target
pt2 = MinMaxScaler()
pt2.fit(y)
y = pt2.transform(y)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X, y, epochs=200, batch_size=8, verbose=0)
# define a row of new data
row = [13]
# transform the input data
X_new = pt1.transform([row])
# make prediction
yhat = model.predict(X_new)
# invert transform on prediction
yhat = pt2.inverse_transform(yhat)
# report prediction
print('f(%s) = %.3f' % (row, yhat[0]))
运行该示例使模型适合整个数据集,并对单行新数据进行预测。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到输入 13 导致输出 62(千瑞典克朗)。
f([13]) = 62.595
进一步阅读
如果您想更深入地了解这个主题,本节将提供更多资源。
教程
摘要
在本教程中,您发现了如何为瑞典汽车保险回归数据集开发多层感知机神经网络模型。
具体来说,您了解到:
- 如何加载和总结瑞典汽车保险数据集,并使用结果建议数据准备和模型配置使用。
- 如何探索数据集上简单 MLP 模型和数据转换的学习动态。
- 如何对模型表现进行稳健的估计,调整模型表现并对新数据进行预测。
你有什么问题吗?
在下面的评论中提问,我会尽力回答。
如何开发预测电离层扰动的神经网络
原文:https://machinelearningmastery.com/predicting-disturbances-in-the-ionosphere/
为新数据集开发神经网络预测模型可能具有挑战性。
一种方法是首先检查数据集,并为哪些模型可能起作用提出想法,然后探索数据集上简单模型的学习动态,最后利用强大的测试工具为数据集开发和调整模型。
该过程可用于开发用于分类和回归预测建模问题的有效神经网络模型。
在本教程中,您将发现如何为电离层二进制分类数据集开发多层感知机神经网络模型。
完成本教程后,您将知道:
- 如何加载和总结电离层数据集,并使用结果建议数据准备和模型配置使用。
- 如何探索数据集上简单 MLP 模型的学习动态。
- 如何对模型表现进行稳健估计,调整模型表现,并对新数据进行预测。
我们开始吧。

如何开发一个预测电离层扰动的神经网络
图片由谢尔盖·劳利耶夫提供,版权所有。
教程概述
本教程分为四个部分;它们是:
- 电离层二进制分类数据集
- 神经网络学习动力学
- 评估和调整 MLP 模型
- 最终模型和做出预测
电离层二进制分类数据集
第一步是定义和探索数据集。
我们将使用“电离层”标准二进制分类数据集。
这个数据集包括预测一个结构是否在大气中,给定雷达回波。
您可以在此了解有关数据集的更多信息:
您可以在下面看到数据集的前几行。
1,0,0.99539,-0.05889,0.85243,0.02306,0.83398,-0.37708,1,0.03760,0.85243,-0.17755,0.59755,-0.44945,0.60536,-0.38223,0.84356,-0.38542,0.58212,-0.32192,0.56971,-0.29674,0.36946,-0.47357,0.56811,-0.51171,0.41078,-0.46168,0.21266,-0.34090,0.42267,-0.54487,0.18641,-0.45300,g
1,0,1,-0.18829,0.93035,-0.36156,-0.10868,-0.93597,1,-0.04549,0.50874,-0.67743,0.34432,-0.69707,-0.51685,-0.97515,0.05499,-0.62237,0.33109,-1,-0.13151,-0.45300,-0.18056,-0.35734,-0.20332,-0.26569,-0.20468,-0.18401,-0.19040,-0.11593,-0.16626,-0.06288,-0.13738,-0.02447,b
1,0,1,-0.03365,1,0.00485,1,-0.12062,0.88965,0.01198,0.73082,0.05346,0.85443,0.00827,0.54591,0.00299,0.83775,-0.13644,0.75535,-0.08540,0.70887,-0.27502,0.43385,-0.12062,0.57528,-0.40220,0.58984,-0.22145,0.43100,-0.17365,0.60436,-0.24180,0.56045,-0.38238,g
1,0,1,-0.45161,1,1,0.71216,-1,0,0,0,0,0,0,-1,0.14516,0.54094,-0.39330,-1,-0.54467,-0.69975,1,0,0,1,0.90695,0.51613,1,1,-0.20099,0.25682,1,-0.32382,1,b
1,0,1,-0.02401,0.94140,0.06531,0.92106,-0.23255,0.77152,-0.16399,0.52798,-0.20275,0.56409,-0.00712,0.34395,-0.27457,0.52940,-0.21780,0.45107,-0.17813,0.05982,-0.35575,0.02309,-0.52879,0.03286,-0.65158,0.13290,-0.53206,0.02431,-0.62197,-0.05707,-0.59573,-0.04608,-0.65697,g
...
我们可以看到这些值都是数字,可能在[-1,1]的范围内。这表明可能不需要某种类型的缩放。
我们还可以看到标签是一个字符串(“ g ”和“ b ”),这表明在拟合模型之前需要将值编码为 0 和 1。
我们可以直接从网址将数据集加载为熊猫数据帧;例如:
# load the ionosphere dataset and summarize the shape
from pandas import read_csv
# define the location of the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
# load the dataset
df = read_csv(url, header=None)
# summarize shape
print(df.shape)
运行该示例直接从 URL 加载数据集,并报告数据集的形状。
在这种情况下,我们可以看到数据集有 35 个变量(34 个输入和一个输出),数据集有 351 行数据。
对于神经网络来说,这不是很多行的数据,这表明一个小的网络,也许带有正则化,将是合适的。
它还建议使用 k 倍交叉验证将是一个好主意,因为它将给出比训练/测试分割更可靠的模型表现估计,并且因为单个模型将在几秒钟内适合最大数据集,而不是几小时或几天。
(351, 35)
接下来,我们可以通过查看汇总统计数据和数据图来了解更多关于数据集的信息。
# show summary statistics and plots of the ionosphere dataset
from pandas import read_csv
from matplotlib import pyplot
# define the location of the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
# load the dataset
df = read_csv(url, header=None)
# show summary statistics
print(df.describe())
# plot histograms
df.hist()
pyplot.show()
运行该示例首先加载之前的数据,然后打印每个变量的汇总统计信息。
我们可以看到每个变量的平均值都在十位数,取值范围从-1 到 1。这证实了缩放数据可能不是必需的。
0 1 2 ... 31 32 33
count 351.000000 351.0 351.000000 ... 351.000000 351.000000 351.000000
mean 0.891738 0.0 0.641342 ... -0.003794 0.349364 0.014480
std 0.311155 0.0 0.497708 ... 0.513574 0.522663 0.468337
min 0.000000 0.0 -1.000000 ... -1.000000 -1.000000 -1.000000
25% 1.000000 0.0 0.472135 ... -0.242595 0.000000 -0.165350
50% 1.000000 0.0 0.871110 ... 0.000000 0.409560 0.000000
75% 1.000000 0.0 1.000000 ... 0.200120 0.813765 0.171660
max 1.000000 0.0 1.000000 ... 1.000000 1.000000 1.000000
然后为每个变量创建直方图。
我们可以看到许多变量具有高斯或类高斯分布。
我们在每个变量上使用幂变换可能会有一些好处,以便使概率分布不那么偏斜,这可能会提高模型表现。
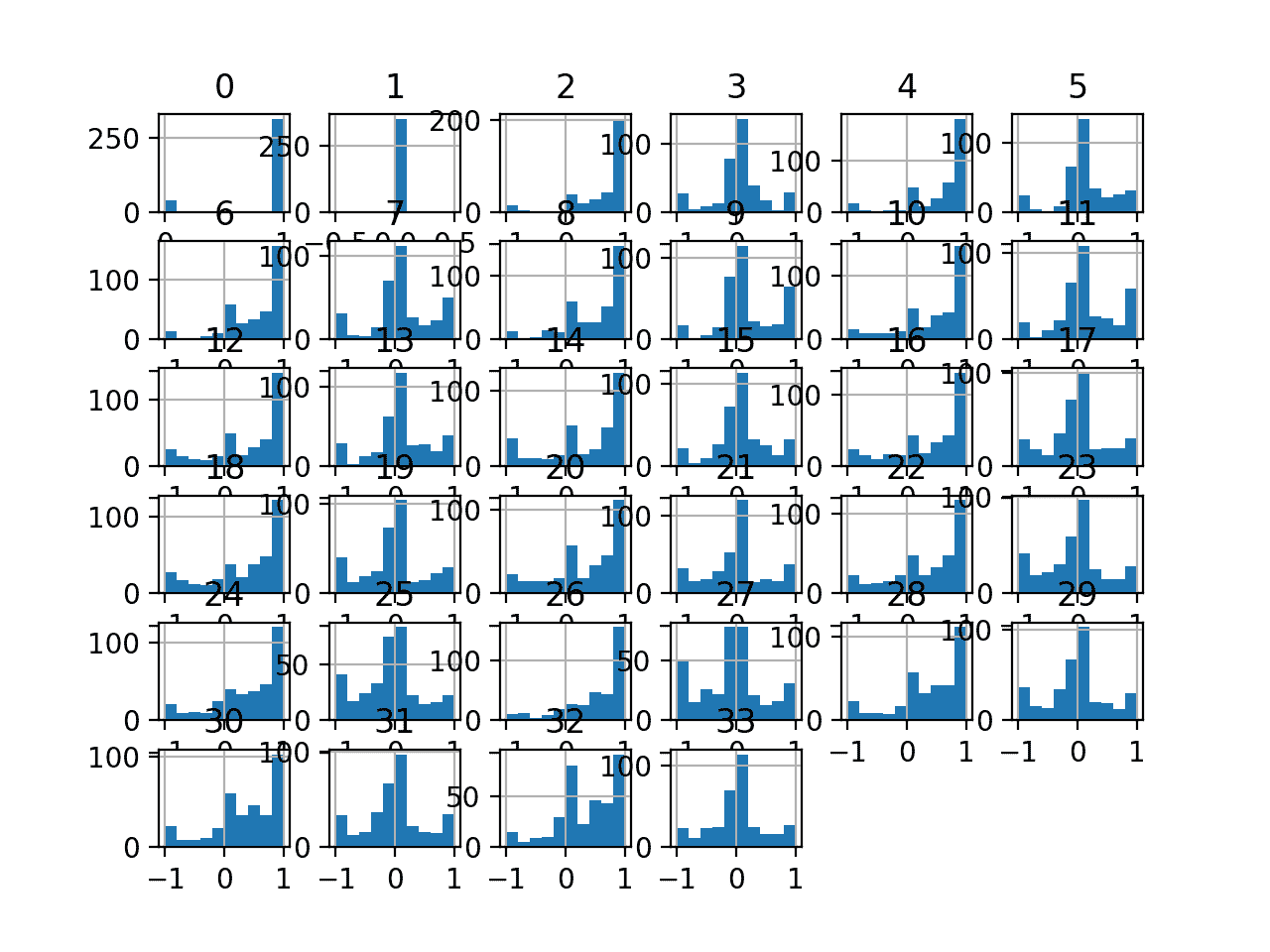
电离层分类数据集的直方图
现在我们已经熟悉了数据集,让我们探索如何开发一个神经网络模型。
神经网络学习动力学
我们将使用张量流为数据集开发一个多层感知机(MLP)模型。
我们无法知道什么样的学习超参数的模型架构对这个数据集是好的或最好的,所以我们必须实验并发现什么是好的。
假设数据集很小,小的批量可能是个好主意,例如 16 或 32 行。开始时使用亚当版本的随机梯度下降是一个好主意,因为它会自动适应学习速率,并且在大多数数据集上运行良好。
在我们认真评估模型之前,最好回顾学习动态,调整模型架构和学习配置,直到我们有稳定的学习动态,然后看看如何从模型中获得最大收益。
我们可以通过使用数据的简单训练/测试分割和学习曲线的复习图来做到这一点。这将有助于我们了解自己是学习过度还是学习不足;然后我们可以相应地调整配置。
首先,我们必须确保所有输入变量都是浮点值,并将目标标签编码为整数值 0 和 1。
...
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
接下来,我们可以将数据集分成输入和输出变量,然后分成 67/33 训练集和测试集。
...
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
我们可以定义一个最小 MLP 模型。在这种情况下,我们将使用一个具有 10 个节点的隐藏层和一个输出层(任意选择)。我们将使用隐藏层中的 ReLU 激活函数和 he_normal 权重初始化,作为一个整体,它们是一个很好的实践。
模型的输出是二进制分类的 sigmoid 激活,我们将最小化二进制交叉熵损失。
...
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
我们将使模型适合 200 个训练时期(任意选择),批量大小为 32,因为它是一个小数据集。
我们正在原始数据上拟合模型,我们认为这可能是一个好主意,但这是一个重要的起点。
...
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=32, verbose=0, validation_data=(X_test,y_test))
在训练结束时,我们将评估模型在测试数据集上的表现,并将表现报告为分类精确率。
...
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Accuracy: %.3f' % score)
最后,我们将绘制训练和测试集上交叉熵损失的学习曲线。
...
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Cross Entropy')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
将所有这些联系在一起,下面列出了在电离层数据集上评估我们的第一个 MLP 的完整示例。
# fit a simple mlp model on the ionosphere and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=32, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Accuracy: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Cross Entropy')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
运行该示例首先在训练数据集上拟合模型,然后在测试数据集上报告分类精确率。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到模型达到了大约 88%的准确率,这是一个很好的表现基线,我们或许可以在此基础上进行改进。
Accuracy: 0.888
然后创建列车和测试集上的损耗线图。
我们可以看到模型似乎收敛了,但是对训练数据集进行了过拟合。
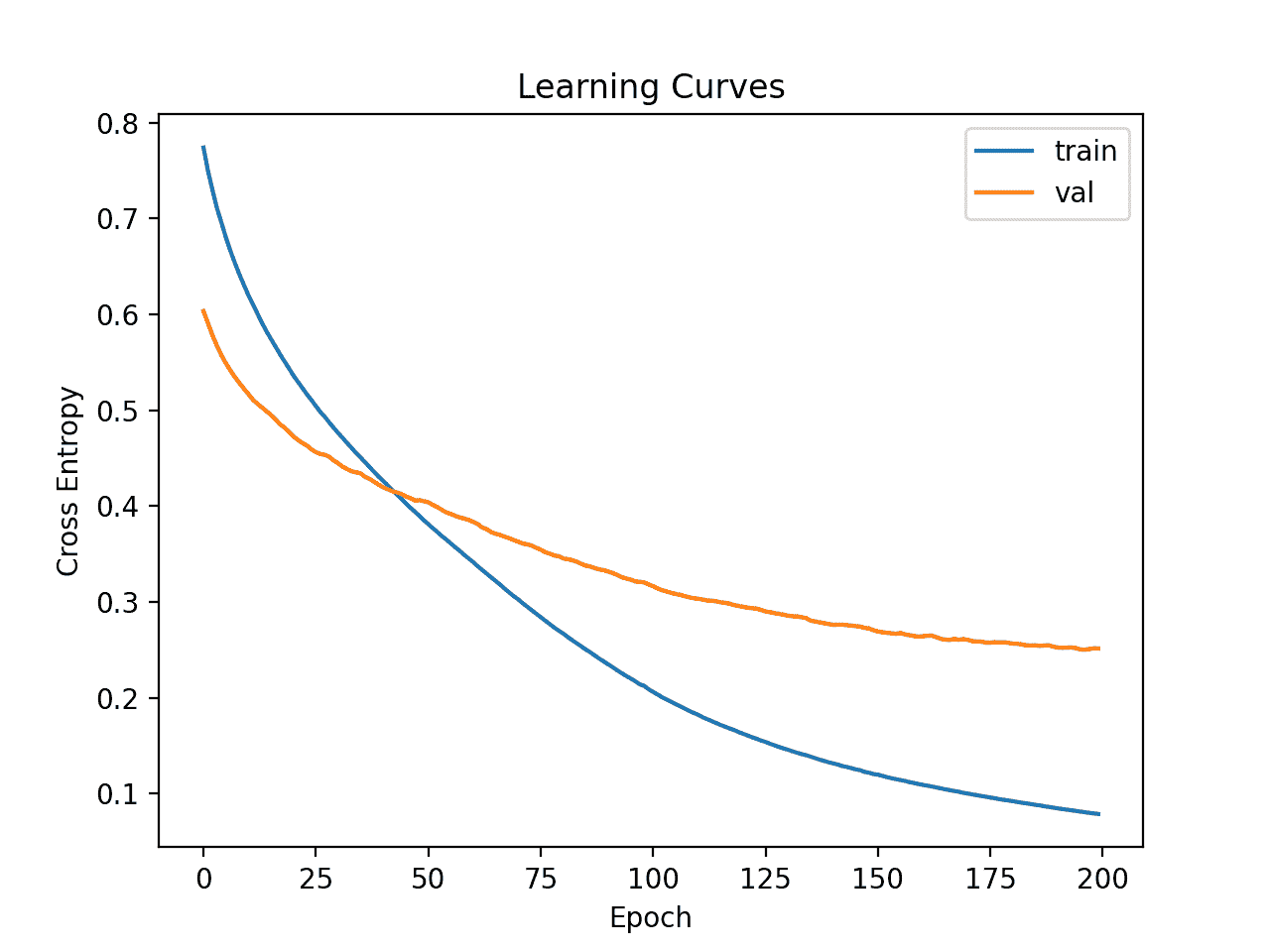
电离层数据集上简单 MLP 的学习曲线
让我们试着增加模型的容量。
这将减缓相同学习超参数的学习,并可能提供更好的准确性。
我们将添加带有八个节点的第二个隐藏层,任意选择。
...
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))
下面列出了完整的示例。
# fit a deeper mlp model on the ionosphere and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=32, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Accuracy: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Cross Entropy')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
运行该示例首先在训练数据集上拟合模型,然后在测试数据集上报告精确率。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到准确率略有提高,约为 93%,尽管训练/测试分割的高方差意味着该评估不可靠。
Accuracy: 0.931
然后绘制列车和测试集上损失的学习曲线。我们可以看到,模型似乎仍然表现出过度拟合的行为。
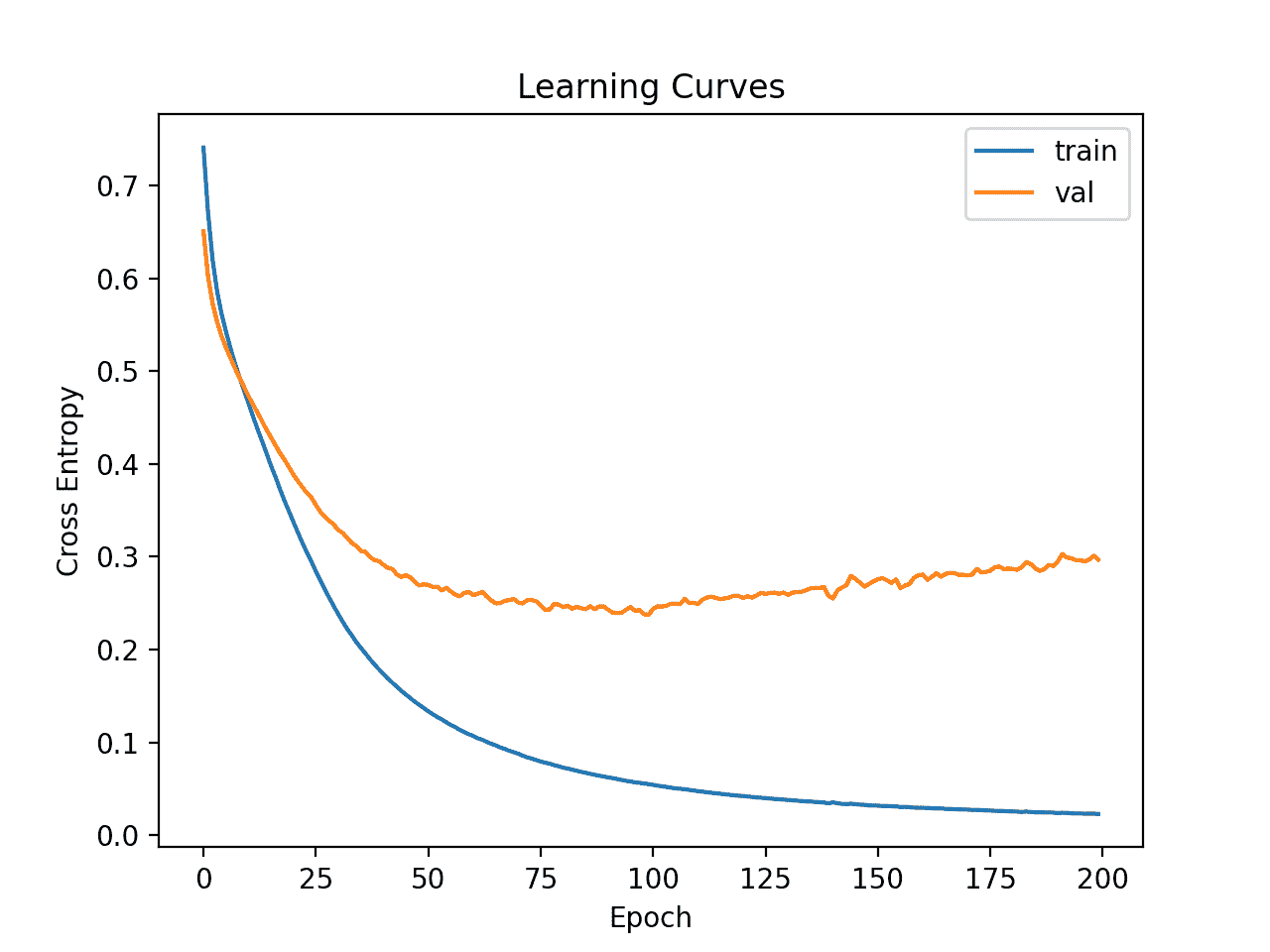
电离层数据集上更深 MLP 的学习曲线
最后,我们可以尝试更广泛的网络。
我们将第一个隐藏层的节点数量从 10 个增加到 50 个,第二个隐藏层的节点数量从 8 个增加到 10 个。
这将增加模型的容量,减慢学习速度,并可能进一步提高结果。
...
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))
我们还将把训练期从 200 个减少到 100 个。
...
# fit the model
history = model.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0, validation_data=(X_test,y_test))
下面列出了完整的示例。
# fit a wider mlp model on the ionosphere and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
history = model.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Accuracy: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Cross Entropy')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
运行该示例首先在训练数据集上拟合模型,然后在测试数据集上报告精确率。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,模型获得了更好的准确性分数,其值约为 94%。我们将暂时忽略模型表现。
Accuracy: 0.940
创建的学习曲线的线图表明,该模型实现了合理的拟合,并且有足够的时间收敛。
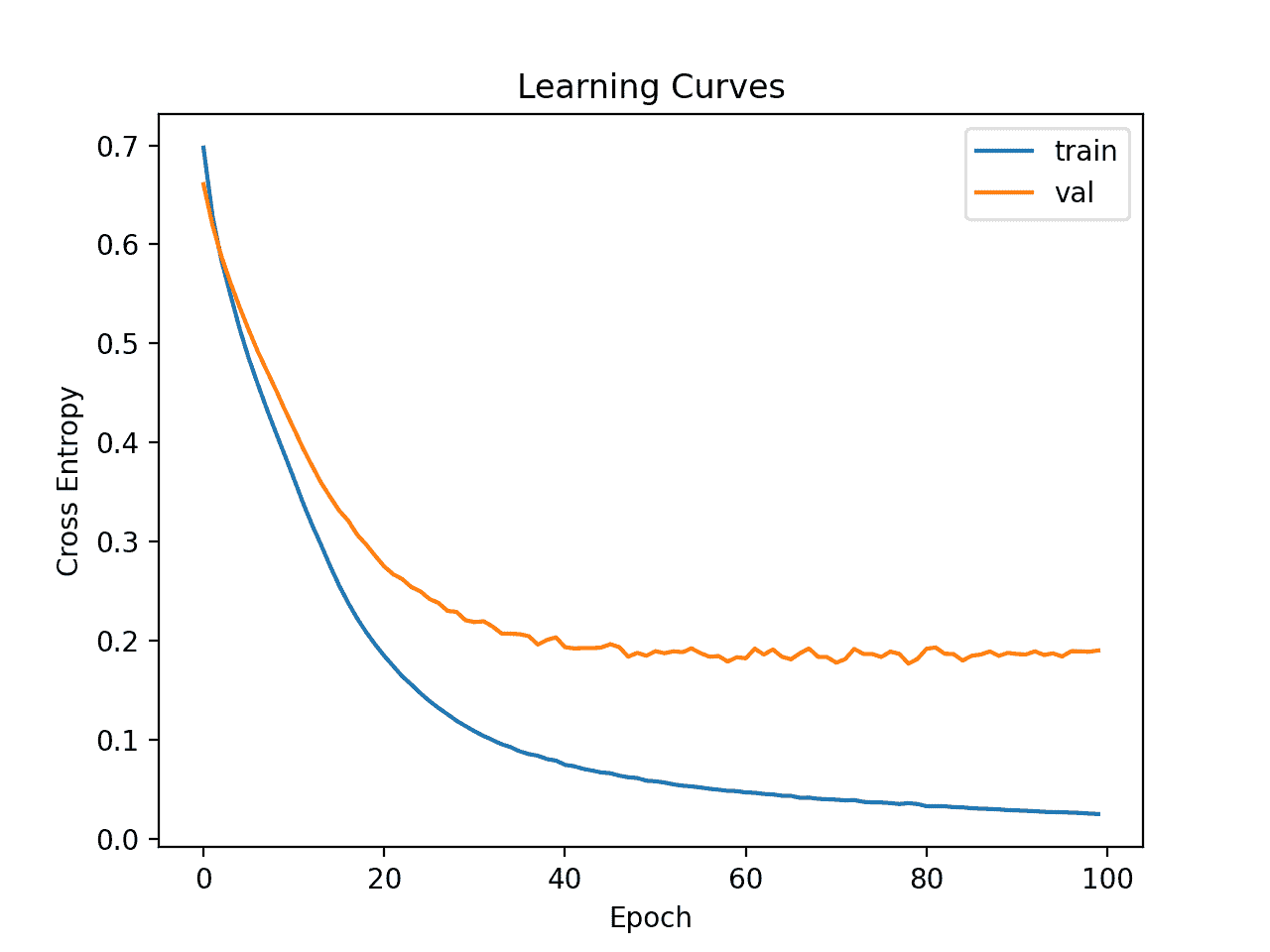
电离层数据集上的广义 MLP 学习曲线
现在我们已经对数据集上的简单 MLP 模型的学习动态有了一些了解,我们可以考虑评估模型的表现以及调整模型的配置。
评估和调整 MLP 模型
k 倍交叉验证程序可以提供更可靠的 MLP 表现估计,尽管它可能非常慢。
这是因为 k 模型必须拟合和评估。当数据集规模较小时,例如电离层数据集,这不是问题。
我们可以使用stratifiedfold类手动枚举每个折叠,拟合模型,对其进行评估,然后在程序结束时报告评估分数的平均值。
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# fit and evaluate the model...
...
...
# summarize all scores
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))
我们可以使用这个框架,通过一系列不同的数据准备、模型架构和学习配置,来开发 MLP 模型表现的可靠估计。
重要的是,在使用 k-fold 交叉验证来估计表现之前,我们首先了解了上一节中模型在数据集上的学习动态。如果我们开始直接调整模型,我们可能会得到好的结果,但如果没有,我们可能不知道为什么,例如,模型过度或拟合不足。
如果我们再次对模型进行大的更改,最好返回并确认模型正在适当收敛。
下面列出了评估前一节中的基本 MLP 模型的框架的完整示例。
# k-fold cross-validation of base model for the ionosphere dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# prepare cross validation
kfold = StratifiedKFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
model.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0)
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))
运行该示例会报告评估程序每次迭代的模型表现,并在运行结束时报告分类精确率的平均值和标准偏差。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到 MLP 模型达到了大约 93.4%的平均精确率。
我们将使用这个结果作为我们的基线,看看我们是否可以实现更好的表现。
>0.972
>0.886
>0.943
>0.886
>0.914
>0.943
>0.943
>1.000
>0.971
>0.886
Mean Accuracy: 0.934 (0.039)
接下来,让我们尝试添加正则化以减少模型的过拟合。
在这种情况下,我们可以在网络的隐藏层之间添加脱落层。例如:
...
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dropout(0.4))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))
下面列出了辍学的 MLP 模式的完整例子。
# k-fold cross-validation of the MLP with dropout for the ionosphere dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Dropout
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# prepare cross validation
kfold = StratifiedKFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dropout(0.4))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
model.fit(X_train, y_train, epochs=100, batch_size=32, verbose=0)
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))
运行报告运行结束时分类准确度的平均值和标准偏差。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到,有辍学的 MLP 模型取得了更好的结果,准确率约为 94.6%,而没有辍学的准确率为 93.4%
Mean Accuracy: 0.946 (0.043)
最后,我们将尝试将批量从 32 减少到 8。
这将导致更多的噪声梯度,也可能降低模型学习问题的速度。
...
# fit the model
model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0)
下面列出了完整的示例。
# k-fold cross-validation of the MLP with dropout for the ionosphere dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import StratifiedKFold
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Dropout
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
y = LabelEncoder().fit_transform(y)
# prepare cross validation
kfold = StratifiedKFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dropout(0.4))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0)
# predict test set
yhat = model.predict_classes(X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean Accuracy: %.3f (%.3f)' % (mean(scores), std(scores)))
运行报告运行结束时分类准确度的平均值和标准偏差。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到,带有脱落的 MLP 模型获得了稍好的结果,准确率约为 94.9%。
Mean Accuracy: 0.949 (0.042)
我们将使用这种配置作为我们的最终模型。
我们可以继续测试模型架构的替代配置(更多或更少的节点或层)、学习超参数(更多或更少的批次)和数据转换。
我把这个作为练习;让我知道你的发现。能不能取得更好的成绩?
在下面的评论中发布你的结果,我很想看看你得到了什么。
接下来,让我们看看如何拟合最终模型并使用它进行预测。
最终模型和做出预测
一旦我们选择了一个模型配置,我们就可以在所有可用的数据上训练一个最终模型,并使用它来对新数据进行预测。
在这种情况下,我们将使用具有脱落和小批量的模型作为最终模型。
我们可以像以前一样准备数据并拟合模型,尽管是在整个数据集上,而不是数据集的训练子集上。
...
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
le = LabelEncoder()
y = le.fit_transform(y)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dropout(0.4))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
然后,我们可以使用这个模型对新数据进行预测。
首先,我们可以定义一行新数据。
...
# define a row of new data
row = [1,0,0.99539,-0.05889,0.85243,0.02306,0.83398,-0.37708,1,0.03760,0.85243,-0.17755,0.59755,-0.44945,0.60536,-0.38223,0.84356,-0.38542,0.58212,-0.32192,0.56971,-0.29674,0.36946,-0.47357,0.56811,-0.51171,0.41078,-0.46168,0.21266,-0.34090,0.42267,-0.54487,0.18641,-0.45300]
注意:我从数据集的第一行取了这一行,期望的标签是一个’ g '。
然后我们可以做一个预测。
...
# make prediction
yhat = model.predict_classes([row])
然后反转预测上的变换,这样我们就可以在正确的标签中使用或解释结果。
...
# invert transform to get label for class
yhat = le.inverse_transform(yhat)
在这种情况下,我们将简单地报告预测。
...
# report prediction
print('Predicted: %s' % (yhat[0]))
将所有这些结合起来,下面列出了为电离层数据集拟合最终模型并使用它对新数据进行预测的完整示例。
# fit a final model and make predictions on new data for the ionosphere dataset
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Dropout
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure all data are floating point values
X = X.astype('float32')
# encode strings to integer
le = LabelEncoder()
y = le.fit_transform(y)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(50, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dropout(0.4))
model.add(Dense(10, activation='relu', kernel_initializer='he_normal'))
model.add(Dropout(0.4))
model.add(Dense(1, activation='sigmoid'))
# compile the model
model.compile(optimizer='adam', loss='binary_crossentropy')
# fit the model
model.fit(X, y, epochs=100, batch_size=8, verbose=0)
# define a row of new data
row = [1,0,0.99539,-0.05889,0.85243,0.02306,0.83398,-0.37708,1,0.03760,0.85243,-0.17755,0.59755,-0.44945,0.60536,-0.38223,0.84356,-0.38542,0.58212,-0.32192,0.56971,-0.29674,0.36946,-0.47357,0.56811,-0.51171,0.41078,-0.46168,0.21266,-0.34090,0.42267,-0.54487,0.18641,-0.45300]
# make prediction
yhat = model.predict_classes([row])
# invert transform to get label for class
yhat = le.inverse_transform(yhat)
# report prediction
print('Predicted: %s' % (yhat[0]))
运行该示例使模型适合整个数据集,并对单行新数据进行预测。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到模型为输入行预测了一个“g”标签。
Predicted: g
进一步阅读
如果您想更深入地了解这个主题,本节将提供更多资源。
教程
摘要
在本教程中,您发现了如何为电离层二进制分类数据集开发多层感知机神经网络模型。
具体来说,您了解到:
- 如何加载和总结电离层数据集,并使用结果建议数据准备和模型配置使用。
- 如何探索数据集上简单 MLP 模型的学习动态。
- 如何对模型表现进行稳健的估计,调整模型表现并对新数据进行预测。
你有什么问题吗?
在下面的评论中提问,我会尽力回答。
深度学习神经网络的预测区间
原文:https://machinelearningmastery.com/prediction-intervals-for-deep-learning-neural-networks/
预测间隔为回归问题的预测提供了不确定性的度量。
例如,95%的预测间隔表示 100 次中的 95 次,真实值将落在范围的下限和上限之间。这不同于可能代表不确定区间中心的简单点预测。
在回归预测建模问题上,没有用于计算深度学习神经网络的预测区间的标准技术。然而,可以使用一组模型来估计快速且肮脏的预测区间,这些模型依次提供点预测的分布,从中可以计算区间。
在本教程中,您将发现如何计算深度学习神经网络的预测区间。
完成本教程后,您将知道:
- 预测区间提供了回归预测建模问题的不确定性度量。
- 如何在标准回归问题上开发和评估简单的多层感知机神经网络。
- 如何使用一组神经网络模型计算和报告预测区间。
我们开始吧。

深度学习神经网络的预测间隔
摄影:尤金 _o ,版权所有。
教程概述
本教程分为三个部分;它们是:
- 预测数的变化范围
- 回归的神经网络
- 神经网络预测区间
预测数的变化范围
通常,回归问题的预测模型(即预测数值)进行点预测。
这意味着他们预测一个单一的值,但没有给出任何关于预测的不确定性的指示。
根据定义,预测是一种估计或近似,包含一些不确定性。不确定性来自模型本身的误差和输入数据中的噪声。该模型是输入变量和输出变量之间关系的近似。
预测区间是对预测不确定性的量化。
它为结果变量的估计提供了一个概率上下限。
单个未来观测值的预测区间是一个在特定置信度下包含从分布中随机选择的未来观测值的区间。
—第 27 页,统计区间:从业者和研究者指南,2017。
使用回归模型进行预测时,最常用的是预测间隔,其中预测的是数量。
预测区间围绕着模型做出的预测,并有望涵盖真实结果的范围。
有关一般预测间隔的更多信息,请参见教程:
现在我们已经熟悉了什么是预测区间,我们可以考虑如何计算神经网络的区间。让我们首先定义一个回归问题和一个神经网络模型来解决它。
回归的神经网络
在本节中,我们将定义一个回归预测建模问题和一个神经网络模型来解决它。
首先,让我们介绍一个标准回归数据集。我们将使用房屋数据集。
外壳数据集是一个标准的机器学习数据集,包括 506 行数据,有 13 个数字输入变量和一个数字目标变量。
使用三次重复的重复分层 10 倍交叉验证的测试工具,一个简单的模型可以获得大约 6.6 的平均绝对误差(MAE)。一个表现最好的模型可以在同一个测试线束上达到 1.9 左右的 MAE。这提供了此数据集的预期表现范围。
该数据集包括预测美国波士顿郊区的房价。
不需要下载数据集;我们将自动下载它作为我们工作示例的一部分。
下面的示例将数据集下载并加载为熊猫数据框,并总结了数据集的形状和前五行数据。
# load and summarize the housing dataset
from pandas import read_csv
from matplotlib import pyplot
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
dataframe = read_csv(url, header=None)
# summarize shape
print(dataframe.shape)
# summarize first few lines
print(dataframe.head())
运行该示例确认了 506 行数据、13 个输入变量和一个数字目标变量(总共 14 个)。我们还可以看到,所有的输入变量都是数字。
(506, 14)
0 1 2 3 4 5 ... 8 9 10 11 12 13
0 0.00632 18.0 2.31 0 0.538 6.575 ... 1 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0 0.469 6.421 ... 2 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0 0.469 7.185 ... 2 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0 0.458 6.998 ... 3 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0 0.458 7.147 ... 3 222.0 18.7 396.90 5.33 36.2
[5 rows x 14 columns]
接下来,我们可以为建模准备数据集。
首先将数据集拆分为输入和输出列,然后将行拆分为训练和测试数据集。
在这种情况下,我们将使用大约 67%的行来训练模型,剩下的 33%用于估计模型的表现。
...
# split into input and output values
X, y = values[:,:-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67)
在本教程中,您可以了解有关列车测试分割的更多信息:
然后,我们将缩放所有输入列(变量),使其范围为 0-1,称为数据规范化,这在使用神经网络模型时是一种很好的做法。
...
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
在本教程中,您可以了解更多关于使用最小最大缩放器规范化输入数据的信息:
下面列出了为建模准备数据的完整示例。
# load and prepare the dataset for modeling
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
dataframe = read_csv(url, header=None)
values = dataframe.values
# split into input and output values
X, y = values[:,:-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67)
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# summarize
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
运行该示例会像以前一样加载数据集,然后将列拆分为输入和输出元素,将行拆分为训练集和测试集,最后将所有输入变量缩放到范围[0,1]
打印了列车和测试集的形状,显示我们有 339 行来训练模型,167 行来评估模型。
(339, 13) (167, 13) (339,) (167,)
接下来,我们可以在数据集上定义、训练和评估多层感知机(MLP)模型。
我们将定义一个简单的模型,它有两个隐藏层和一个预测数值的输出层。我们将使用 ReLU 激活函数和 he 权重初始化,这是一个很好的实践。
每个隐藏层中的节点数是经过一点点尝试和错误后选择的。
...
# define neural network model
features = X_train.shape[1]
model = Sequential()
model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features))
model.add(Dense(5, kernel_initializer='he_normal', activation='relu'))
model.add(Dense(1))
我们将使用具有接近默认学习率和动量值的随机梯度下降的有效亚当版本,并使用均方误差(MSE)损失函数拟合模型,这是回归预测建模问题的标准。
...
# compile the model and specify loss and optimizer
opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999)
model.compile(optimizer=opt, loss='mse')
您可以在本教程中了解关于 Adam 优化算法的更多信息:
该模型将适用于 300 个时代,批量为 16 个样本。这种配置是经过反复试验后选择的。
...
# fit the model on the training dataset
model.fit(X_train, y_train, verbose=2, epochs=300, batch_size=16)
您可以在本教程中了解有关批次和时期的更多信息:
最后,该模型可用于对测试数据集进行预测,我们可以通过将预测与测试集中的期望值进行比较来评估预测,并计算平均绝对误差(MAE),这是模型表现的一个有用度量。
...
# make predictions on the test set
yhat = model.predict(X_test, verbose=0)
# calculate the average error in the predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
将这些联系在一起,完整的示例如下所示。
# train and evaluate a multilayer perceptron neural network on the housing regression dataset
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
dataframe = read_csv(url, header=None)
values = dataframe.values
# split into input and output values
X, y = values[:, :-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1)
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
# define neural network model
features = X_train.shape[1]
model = Sequential()
model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features))
model.add(Dense(5, kernel_initializer='he_normal', activation='relu'))
model.add(Dense(1))
# compile the model and specify loss and optimizer
opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999)
model.compile(optimizer=opt, loss='mse')
# fit the model on the training dataset
model.fit(X_train, y_train, verbose=2, epochs=300, batch_size=16)
# make predictions on the test set
yhat = model.predict(X_test, verbose=0)
# calculate the average error in the predictions
mae = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % mae)
运行该示例加载和准备数据集,在训练数据集上定义和拟合 MLP 模型,并在测试集上评估其表现。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到,该模型实现了大约 2.3 的平均绝对误差,这优于天真模型,并接近最佳模型。
毫无疑问,通过进一步调整模型,我们可以获得接近最优的表现,但这对于我们研究预测区间来说已经足够好了。
...
Epoch 296/300
22/22 - 0s - loss: 7.1741
Epoch 297/300
22/22 - 0s - loss: 6.8044
Epoch 298/300
22/22 - 0s - loss: 6.8623
Epoch 299/300
22/22 - 0s - loss: 7.7010
Epoch 300/300
22/22 - 0s - loss: 6.5374
MAE: 2.300
接下来,让我们看看如何使用我们的 MLP 模型在住房数据集上计算预测区间。
神经网络预测区间
在本节中,我们将使用上一节中开发的回归问题和模型来开发预测区间。
与线性回归等线性方法相比,计算神经网络等非线性回归算法的预测区间具有挑战性,因为线性回归的预测区间计算量很小。没有标准的技术。
有许多方法可以计算神经网络模型的有效预测区间。我推荐一些列在“进一步阅读”部分的论文来了解更多。
在本教程中,我们将使用一种非常简单的方法,它有很大的扩展空间。我称之为快而脏,因为它快而易算,但有局限性。
它包括拟合多个最终模型(例如 10 到 30 个)。然后,来自集合成员的点预测的分布被用于计算点预测和预测间隔。
例如,一个点预测可以作为来自集合成员的点预测的平均值,95%的预测间隔可以作为与平均值的 1.96 标准偏差。
这是一个简单的高斯预测区间,尽管也可以使用替代方案,例如点预测的最小值和最大值。或者,自举方法可用于在不同的自举样本上训练每个集合成员,点预测的 2.5 和 97.5 百分位数可用作预测区间。
有关引导方法的更多信息,请参见教程:
这些延伸作为练习留着;我们将坚持简单的高斯预测区间。
让我们假设上一节中定义的训练数据集是整个数据集,并且我们正在这个整个数据集上训练一个或多个最终模型。然后,我们可以用测试集上的预测区间进行预测,并评估该区间在未来的有效性。
我们可以通过将上一节中开发的元素分成函数来简化代码。
首先,让我们定义一个函数,用于加载和准备由 URL 定义的回归数据集。
# load and prepare the dataset
def load_dataset(url):
dataframe = read_csv(url, header=None)
values = dataframe.values
# split into input and output values
X, y = values[:, :-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1)
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
return X_train, X_test, y_train, y_test
接下来,我们可以定义一个函数,该函数将在给定训练数据集的情况下定义和训练 MLP 模型,然后返回拟合模型,准备进行预测。
# define and fit the model
def fit_model(X_train, y_train):
# define neural network model
features = X_train.shape[1]
model = Sequential()
model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features))
model.add(Dense(5, kernel_initializer='he_normal', activation='relu'))
model.add(Dense(1))
# compile the model and specify loss and optimizer
opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999)
model.compile(optimizer=opt, loss='mse')
# fit the model on the training dataset
model.fit(X_train, y_train, verbose=0, epochs=300, batch_size=16)
return model
我们需要多个模型来进行点预测,这将定义点预测的分布,从中我们可以估计区间。
因此,我们需要在训练数据集上拟合多个模型。每个模型必须不同,这样才能做出不同的预测。这可以通过给定训练 MLP 模型的随机性质、给定随机初始权重以及给定随机梯度下降优化算法的使用来实现。
模型越多,点预测对模型表现的估计就越好。我会推荐至少 10 个型号,也许 30 个型号之外没什么好处。
下面的函数适合一组模型,并将它们存储在返回的列表中。
出于兴趣,每个拟合模型也在测试集上进行评估,测试集在每个模型拟合后报告。我们预计,每个模型在搁置测试集上的估计表现会略有不同,报告的分数将有助于我们确认这一预期。
# fit an ensemble of models
def fit_ensemble(n_members, X_train, X_test, y_train, y_test):
ensemble = list()
for i in range(n_members):
# define and fit the model on the training set
model = fit_model(X_train, y_train)
# evaluate model on the test set
yhat = model.predict(X_test, verbose=0)
mae = mean_absolute_error(y_test, yhat)
print('>%d, MAE: %.3f' % (i+1, mae))
# store the model
ensemble.append(model)
return ensemble
最后,我们可以使用训练好的模型集合进行点预测,这些点预测可以总结为一个预测区间。
下面的函数实现了这一点。首先,每个模型对输入数据进行点预测,然后计算 95%的预测区间,并返回区间的下、中、上值。
该函数被设计为以一行作为输入,但可以很容易地适应多行。
# make predictions with the ensemble and calculate a prediction interval
def predict_with_pi(ensemble, X):
# make predictions
yhat = [model.predict(X, verbose=0) for model in ensemble]
yhat = asarray(yhat)
# calculate 95% gaussian prediction interval
interval = 1.96 * yhat.std()
lower, upper = yhat.mean() - interval, yhat.mean() + interval
return lower, yhat.mean(), upper
最后,我们可以调用这些函数。
首先,加载和准备数据集,然后定义和拟合集合。
...
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
X_train, X_test, y_train, y_test = load_dataset(url)
# fit ensemble
n_members = 30
ensemble = fit_ensemble(n_members, X_train, X_test, y_train, y_test)
然后,我们可以使用测试集中的单行数据,用预测间隔进行预测,然后报告结果。
我们还报告了预期值,我们预计该值将被预测区间覆盖(可能接近 95%的时间;这并不完全准确,只是一个粗略的近似值)。
...
# make predictions with prediction interval
newX = asarray([X_test[0, :]])
lower, mean, upper = predict_with_pi(ensemble, newX)
print('Point prediction: %.3f' % mean)
print('95%% prediction interval: [%.3f, %.3f]' % (lower, upper))
print('True value: %.3f' % y_test[0])
将这些联系在一起,下面列出了使用多层感知机神经网络以预测间隔进行预测的完整示例。
# prediction interval for mlps on the housing regression dataset
from numpy import asarray
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import Adam
# load and prepare the dataset
def load_dataset(url):
dataframe = read_csv(url, header=None)
values = dataframe.values
# split into input and output values
X, y = values[:, :-1], values[:,-1]
# split into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.67, random_state=1)
# scale input data
scaler = MinMaxScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)
return X_train, X_test, y_train, y_test
# define and fit the model
def fit_model(X_train, y_train):
# define neural network model
features = X_train.shape[1]
model = Sequential()
model.add(Dense(20, kernel_initializer='he_normal', activation='relu', input_dim=features))
model.add(Dense(5, kernel_initializer='he_normal', activation='relu'))
model.add(Dense(1))
# compile the model and specify loss and optimizer
opt = Adam(learning_rate=0.01, beta_1=0.85, beta_2=0.999)
model.compile(optimizer=opt, loss='mse')
# fit the model on the training dataset
model.fit(X_train, y_train, verbose=0, epochs=300, batch_size=16)
return model
# fit an ensemble of models
def fit_ensemble(n_members, X_train, X_test, y_train, y_test):
ensemble = list()
for i in range(n_members):
# define and fit the model on the training set
model = fit_model(X_train, y_train)
# evaluate model on the test set
yhat = model.predict(X_test, verbose=0)
mae = mean_absolute_error(y_test, yhat)
print('>%d, MAE: %.3f' % (i+1, mae))
# store the model
ensemble.append(model)
return ensemble
# make predictions with the ensemble and calculate a prediction interval
def predict_with_pi(ensemble, X):
# make predictions
yhat = [model.predict(X, verbose=0) for model in ensemble]
yhat = asarray(yhat)
# calculate 95% gaussian prediction interval
interval = 1.96 * yhat.std()
lower, upper = yhat.mean() - interval, yhat.mean() + interval
return lower, yhat.mean(), upper
# load dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
X_train, X_test, y_train, y_test = load_dataset(url)
# fit ensemble
n_members = 30
ensemble = fit_ensemble(n_members, X_train, X_test, y_train, y_test)
# make predictions with prediction interval
newX = asarray([X_test[0, :]])
lower, mean, upper = predict_with_pi(ensemble, newX)
print('Point prediction: %.3f' % mean)
print('95%% prediction interval: [%.3f, %.3f]' % (lower, upper))
print('True value: %.3f' % y_test[0])
运行该示例依次适合每个集成成员,并在等待测试集上报告其估计表现;最后,作出并报告具有预测区间的单一预测。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
在这种情况下,我们可以看到每个模型的表现略有不同,这证实了我们对模型确实不同的预期。
最后,我们可以看到,集合做出了大约 30.5 的点预测,95%的预测间隔为[26.287,34.822]。我们还可以看到真实值是 28.2,间隔确实捕捉到了这个值,这很棒。
>1, MAE: 2.259
>2, MAE: 2.144
>3, MAE: 2.732
>4, MAE: 2.628
>5, MAE: 2.483
>6, MAE: 2.551
>7, MAE: 2.505
>8, MAE: 2.299
>9, MAE: 2.706
>10, MAE: 2.145
>11, MAE: 2.765
>12, MAE: 3.244
>13, MAE: 2.385
>14, MAE: 2.592
>15, MAE: 2.418
>16, MAE: 2.493
>17, MAE: 2.367
>18, MAE: 2.569
>19, MAE: 2.664
>20, MAE: 2.233
>21, MAE: 2.228
>22, MAE: 2.646
>23, MAE: 2.641
>24, MAE: 2.492
>25, MAE: 2.558
>26, MAE: 2.416
>27, MAE: 2.328
>28, MAE: 2.383
>29, MAE: 2.215
>30, MAE: 2.408
Point prediction: 30.555
95% prediction interval: [26.287, 34.822]
True value: 28.200
如上所述,这是一种快速而肮脏的技术,用于利用神经网络的预测区间进行预测。
有一些简单的扩展,例如使用自举方法来进行可能更可靠的点预测,以及我建议您探索的下面列出的一些论文中描述的更高级的技术。
进一步阅读
如果您想更深入地了解这个主题,本节将提供更多资源。
教程
报纸
- 深度学习的高质量预测区间:一种无分布、集合的方法,2018。
- 实际置信区间和预测区间,1994。
文章
- 1.96,维基百科。
摘要
在本教程中,您发现了如何计算深度学习神经网络的预测间隔。
具体来说,您了解到:
- 预测区间提供了回归预测建模问题的不确定性度量。
- 如何在标准回归问题上开发和评估简单的多层感知机神经网络。
- 如何使用一组神经网络模型计算和报告预测区间。
你有什么问题吗?
在下面的评论中提问,我会尽力回答。
PyTorch 教程:如何用 Python 开发深度学习模型
原文:https://machinelearningmastery.com/pytorch-tutorial-develop-deep-learning-models/
最后更新于 2020 年 8 月 27 日
具有深度学习的预测建模是现代开发人员需要了解的技能。
PyTorch 是脸书开发和维护的第一个开源深度学习框架。
从本质上来说,PyTorch 是一个数学库,允许您对基于图形的模型进行高效计算和自动微分。直接实现这一点是具有挑战性的,尽管谢天谢地,现代的 PyTorch API 提供了类和习惯用法,允许您轻松开发一套深度学习模型。
在本教程中,您将发现一个在 PyTorch 中开发深度学习模型的分步指南。
完成本教程后,您将知道:
- Torch 和 PyTorch 的区别以及如何安装和确认 PyTorch 工作正常。
- PyTorch 模型的五步生命周期以及如何定义、拟合和评估模型。
- 如何为回归、分类和预测建模任务开发 PyTorch 深度学习模型?
我们开始吧。

PyTorch 教程-如何开发深度学习模型
图片由迪米特里·B提供。,保留部分权利。
PyTorch 教程概述
本教程的重点是将 PyTorch API 用于常见的深度学习模型开发任务;我们不会深入学习数学和理论。为此,我推荐从这本优秀的书开始。
在 python 中学习深度学习的最好方法是做。一头扎进去。你可以回头再找更多的理论。
我已经将每个代码示例设计成使用最佳实践和独立的,这样您就可以将它直接复制并粘贴到您的项目中,并根据您的特定需求进行调整。这将让你有一个很好的开端来尝试从官方文档中找出应用编程接口。
这是一个大型教程,因此,它分为三个部分;它们是:
- 如何安装 PyTorch
- 什么是火炬和 PyTorch?
- 如何安装 PyTorch
- 如何确认 PyTorch 已安装
- PyTorch 深度学习模型生命周期
- 第一步:准备数据
- 步骤 2:定义模型
- 第三步:训练模型
- 步骤 4:评估模型
- 第五步:做预测
- 如何开发 PyTorch 深度学习模型
- 如何开发二元分类的 MLP
- 如何开发多类分类的 MLP
- 如何开发回归 MLP
- 如何开发一个用于图像分类的有线电视网络
你可以用 Python 做深度学习!
完成本教程。最多需要 60 分钟!
你不需要什么都懂(至少现在不需要)。你的目标是把教程从头到尾看一遍,并得到一个结果。你不需要第一遍就明白所有的事情。边走边列出你的问题。大量使用 API 文档来了解您正在使用的所有功能。
你不需要 Prophet 道数学。数学是描述算法如何工作的简洁方式,特别是来自线性代数、概率和微积分的工具。这些不是你可以用来学习算法如何工作的唯一工具。您还可以使用代码并探索具有不同输入和输出的算法行为。知道数学不会告诉你选择什么算法或者如何最好地配置它。你只能通过精心控制的实验来发现这一点。
你不需要知道算法是如何工作的。了解这些限制以及如何配置深度学习算法非常重要。但是关于算法的学习可以在以后进行。你需要长时间慢慢积累这些算法知识。今天,从适应平台开始。
不需要做 Python 程序员。如果你不熟悉 Python 语言,它的语法会很直观。就像其他语言一样,关注函数调用(例如 function())和赋值(例如 a =“b”)。这会让你大受鼓舞。你是一个开发者;你知道如何快速掌握一门语言的基础知识。开始吧,稍后再深入细节。
不需要成为深度学习专家。你可以在后面学习各种算法的好处和局限性,还有很多教程可以阅读,以便在深度学习项目的步骤上复习。
1.如何安装 PyTorch
在本节中,您将发现什么是 PyTorch,如何安装它,以及如何确认它安装正确。
1.1.什么是火炬和 PyTorch?
PyTorch 是脸书开发维护的一个用于深度学习的开源 Python 库。
该项目始于 2016 年,很快成为开发人员和研究人员的流行框架。
Torch ( Torch7 )是用 C 语言编写的深度学习开源项目,一般通过 Lua 接口使用。这是 PyTorch 的前身项目,现在已不再积极开发。PyTorch 在名称中包含“ Torch ”,以“ Py ”前缀确认之前的 Torch 库,表示新项目的 Python 重点。
PyTorch API 简单而灵活,使其成为学者和研究人员在开发新的深度学习模型和应用程序时的最爱。广泛的使用导致了许多特定应用的扩展(例如文本、计算机视觉和音频数据),并且可能预先训练了可以直接使用的模型。因此,它可能是最受学者欢迎的图书馆。
与像 Keras 这样更简单的界面相比,PyTorch 的灵活性是以易用性为代价的,尤其是对于初学者来说。选择使用 PyTorch 而不是 Keras,放弃了一些易用性、略陡的学习曲线、更多的代码以获得更大的灵活性,或许还有更有活力的学术社区。
1.2.如何安装 PyTorch
在安装 PyTorch 之前,请确保您安装了 Python,例如 Python 3.6 或更高版本。
如果没有安装 Python,可以使用 Anaconda 安装。本教程将向您展示如何:
- 如何用 Anaconda 设置机器学习的 Python 环境
安装 PyTorch 开源深度学习库的方法有很多。
在您的工作站上安装 PyTorch 最常见,也可能是最简单的方法是使用 pip。
例如,在命令行上,您可以键入:
sudo pip install torch
深度学习最受欢迎的应用可能是计算机视觉,PyTorch 计算机视觉包叫做“ torchvision ”
强烈建议安装 torchvision,安装方式如下:
sudo pip install torchvision
如果您更喜欢使用特定于您的平台或软件包管理器的安装方法,您可以在此查看完整的安装说明列表:
- pytorch 安装指南
现在没有必要设置 GPU。
本教程中的所有示例在现代中央处理器上都可以正常工作。如果您想为您的 GPU 配置 PyTorch,您可以在完成本教程后进行配置。不要分心!
1.3.如何确认 PyTorch 已安装
一旦安装了 PyTorch,确认库安装成功并且您可以开始使用它是很重要的。
不要跳过这一步。
如果 PyTorch 安装不正确或在此步骤中出现错误,您将无法在以后运行这些示例。
创建一个名为 versions.py 的新文件,并将以下代码复制粘贴到文件中。
# check pytorch version
import torch
print(torch.__version__)
保存文件,然后打开命令行,将目录更改为保存文件的位置。
然后键入:
python versions.py
然后,您应该会看到如下输出:
1.3.1
这确认了 PyTorch 安装正确,并且我们都使用相同的版本。
这也向您展示了如何从命令行运行 Python 脚本。我建议以这种方式从命令行运行所有代码,而不是从笔记本或 IDE 运行。
2.PyTorch 深度学习模型生命周期
在这一节中,您将发现深度学习模型的生命周期以及可以用来定义模型的 PyTorch API。
模型有一个生命周期,这个非常简单的知识为建模数据集和理解 PyTorch API 提供了基础。
生命周期中的五个步骤如下:
- 1.准备数据。
- 2.定义模型。
- 3.训练模型。
- 4.评估模型。
- 5.做预测。
让我们依次仔细看看每一步。
注意:使用 PyTorch API 实现这些步骤的方法有很多,虽然我的目的是向您展示最简单的,或者最常见的,或者最惯用的。
如果你发现了更好的方法,请在下面的评论中告诉我。
第一步:准备数据
第一步是加载和准备数据。
神经网络模型需要数值输入数据和数值输出数据。
您可以使用标准 Python 库来加载和准备表格数据,如 CSV 文件。例如,Pandas 可以用来加载你的 CSV 文件,Sklearn 的工具可以用来编码分类数据,比如类标签。
PyTorch 提供了数据集类,您可以扩展和定制该类来加载数据集。
例如,数据集对象的构造函数可以加载数据文件(例如 CSV 文件)。然后,您可以覆盖可用于获取数据集长度(行数或样本数)的 len() 函数,以及可用于通过索引获取特定样本的 getitem() 函数。
加载数据集时,还可以执行任何所需的转换,如缩放或编码。
自定义数据集类的框架如下。
# dataset definition
class CSVDataset(Dataset):
# load the dataset
def __init__(self, path):
# store the inputs and outputs
self.X = ...
self.y = ...
# number of rows in the dataset
def __len__(self):
return len(self.X)
# get a row at an index
def __getitem__(self, idx):
return [self.X[idx], self.y[idx]]
加载后,PyTorch 提供数据加载器类在模型的训练和评估过程中导航数据集实例。
可以为训练数据集、测试数据集甚至验证数据集创建数据加载器实例。
random_split()函数可用于将数据集分割成训练集和测试集。分割后,可以将从数据集中选择的行提供给数据加载器,以及批次大小和数据是否应该在每个时期进行混洗。
例如,我们可以通过传入数据集中选定的行样本来定义数据加载器。
...
# create the dataset
dataset = CSVDataset(...)
# select rows from the dataset
train, test = random_split(dataset, [[...], [...]])
# create a data loader for train and test sets
train_dl = DataLoader(train, batch_size=32, shuffle=True)
test_dl = DataLoader(test, batch_size=1024, shuffle=False)
一旦定义,就可以枚举数据加载器,每次迭代产生一批样本。
...
# train the model
for i, (inputs, targets) in enumerate(train_dl):
...
步骤 2:定义模型
下一步是定义一个模型。
在 PyTorch 中定义模型的习惯用法包括定义一个扩展模块类的类。
您的类的构造函数定义了模型的层,forward()函数是定义如何通过模型的定义层向前传播输入的覆盖。
有很多层可用,例如线性用于全连接层, Conv2d 用于卷积层, MaxPool2d 用于汇集层。
激活函数也可以定义为图层,如 ReLU 、 Softmax 、 Sigmoid 。
下面是一个简单的一层 MLP 模型的例子。
# model definition
class MLP(Module):
# define model elements
def __init__(self, n_inputs):
super(MLP, self).__init__()
self.layer = Linear(n_inputs, 1)
self.activation = Sigmoid()
# forward propagate input
def forward(self, X):
X = self.layer(X)
X = self.activation(X)
return X
在构造函数中定义层之后,也可以初始化给定层的权重。
...
xavier_uniform_(self.layer.weight)
第三步:训练模型
训练过程需要定义损失函数和优化算法。
常见的损失函数包括:
有关损失函数的更多信息,请参见教程:
随机梯度下降用于优化,标准算法由 SGD 类提供,不过也有其他版本的算法,如亚当。
# define the optimization
criterion = MSELoss()
optimizer = SGD(model.parameters(), lr=0.01, momentum=0.9)
训练模型包括为训练数据集枚举数据加载器。
首先,训练时期的数量需要一个循环。然后对于随机梯度下降的小批量需要一个内环。
...
# enumerate epochs
for epoch in range(100):
# enumerate mini batches
for i, (inputs, targets) in enumerate(train_dl):
...
模型的每次更新都涉及相同的一般模式,包括:
- 清除最后一个误差梯度。
- 输入通过模型的前向传递。
- 计算模型输出的损失。
- 通过模型反向传播误差。
- 更新模型以减少损失。
例如:
...
# clear the gradients
optimizer.zero_grad()
# compute the model output
yhat = model(inputs)
# calculate loss
loss = criterion(yhat, targets)
# credit assignment
loss.backward()
# update model weights
optimizer.step()
第四步:评估模型
一旦模型合适,就可以在测试数据集上对其进行评估。
这可以通过对测试数据集使用数据加载器并收集测试集的预测,然后将预测与测试集的期望值进行比较并计算表现指标来实现。
...
for i, (inputs, targets) in enumerate(test_dl):
# evaluate the model on the test set
yhat = model(inputs)
...
第五步:做预测
拟合模型可用于对新数据进行预测。
例如,您可能只有一张图像或一行数据,并且想要进行预测。
这要求您将数据包装在 PyTorch Tensor 数据结构中。
张量只是保存数据的 NumPy 数组的 PyTorch 版本。它还允许您在模型图中执行自动微分任务,比如在训练模型时向后调用*(*)。
预测也将是张量,尽管您可以通过从自动微分图中分离张量并调用 NumPy 函数来检索 NumPy 数组。
...
# convert row to data
row = Variable(Tensor([row]).float())
# make prediction
yhat = model(row)
# retrieve numpy array
yhat = yhat.detach().numpy()
现在我们已经在高级别上熟悉了 PyTorch API 和模型生命周期,让我们看看如何从头开始开发一些标准的深度学习模型。
3.如何开发 PyTorch 深度学习模型
在本节中,您将发现如何使用标准深度学习模型开发、评估和进行预测,包括多层感知机(MLP)和卷积神经网络(CNN)。
多层感知机模型,简称 MLP,是一个标准的全连接神经网络模型。
它由节点层组成,其中每个节点连接到上一层的所有输出,每个节点的输出连接到下一层节点的所有输入。
MLP 是具有一个或多个完全连接的层的模型。这种模型适用于表格数据,即每个变量有一列,每个变量有一行的表格或电子表格中的数据。有三个预测建模问题,你可能想探索与 MLP;它们是二元分类、多类分类和回归。
让我们在真实数据集上为每一种情况拟合一个模型。
注:本节模型有效,但未优化。看看能不能提高他们的成绩。在下面的评论中发表你的发现。
3.1.如何开发二元分类的 MLP
我们将使用电离层二进制(两类)分类数据集来演示二进制分类的 MLP。
这个数据集包括预测在给定雷达回波的情况下,大气中是否存在结构。
数据集将使用 Pandas 自动下载,但您可以在这里了解更多信息。
我们将使用标签编码器将字符串标签编码为整数值 0 和 1。该模型将适用于 67%的数据,剩余的 33%将用于评估,使用 train_test_split()功能进行分割。
用“ He Uniform 权重初始化来使用“ relu 激活是一个很好的做法。这种组合对于克服训练深度神经网络模型时消失梯度的问题大有帮助。有关 ReLU 的更多信息,请参见教程:
该模型预测 1 类概率,并使用 sigmoid 激活函数。该模型使用随机梯度下降进行优化,并寻求最小化二元交叉熵损失。
下面列出了完整的示例。
# pytorch mlp for binary classification
from numpy import vstack
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from torch.utils.data import random_split
from torch import Tensor
from torch.nn import Linear
from torch.nn import ReLU
from torch.nn import Sigmoid
from torch.nn import Module
from torch.optim import SGD
from torch.nn import BCELoss
from torch.nn.init import kaiming_uniform_
from torch.nn.init import xavier_uniform_
# dataset definition
class CSVDataset(Dataset):
# load the dataset
def __init__(self, path):
# load the csv file as a dataframe
df = read_csv(path, header=None)
# store the inputs and outputs
self.X = df.values[:, :-1]
self.y = df.values[:, -1]
# ensure input data is floats
self.X = self.X.astype('float32')
# label encode target and ensure the values are floats
self.y = LabelEncoder().fit_transform(self.y)
self.y = self.y.astype('float32')
self.y = self.y.reshape((len(self.y), 1))
# number of rows in the dataset
def __len__(self):
return len(self.X)
# get a row at an index
def __getitem__(self, idx):
return [self.X[idx], self.y[idx]]
# get indexes for train and test rows
def get_splits(self, n_test=0.33):
# determine sizes
test_size = round(n_test * len(self.X))
train_size = len(self.X) - test_size
# calculate the split
return random_split(self, [train_size, test_size])
# model definition
class MLP(Module):
# define model elements
def __init__(self, n_inputs):
super(MLP, self).__init__()
# input to first hidden layer
self.hidden1 = Linear(n_inputs, 10)
kaiming_uniform_(self.hidden1.weight, nonlinearity='relu')
self.act1 = ReLU()
# second hidden layer
self.hidden2 = Linear(10, 8)
kaiming_uniform_(self.hidden2.weight, nonlinearity='relu')
self.act2 = ReLU()
# third hidden layer and output
self.hidden3 = Linear(8, 1)
xavier_uniform_(self.hidden3.weight)
self.act3 = Sigmoid()
# forward propagate input
def forward(self, X):
# input to first hidden layer
X = self.hidden1(X)
X = self.act1(X)
# second hidden layer
X = self.hidden2(X)
X = self.act2(X)
# third hidden layer and output
X = self.hidden3(X)
X = self.act3(X)
return X
# prepare the dataset
def prepare_data(path):
# load the dataset
dataset = CSVDataset(path)
# calculate split
train, test = dataset.get_splits()
# prepare data loaders
train_dl = DataLoader(train, batch_size=32, shuffle=True)
test_dl = DataLoader(test, batch_size=1024, shuffle=False)
return train_dl, test_dl
# train the model
def train_model(train_dl, model):
# define the optimization
criterion = BCELoss()
optimizer = SGD(model.parameters(), lr=0.01, momentum=0.9)
# enumerate epochs
for epoch in range(100):
# enumerate mini batches
for i, (inputs, targets) in enumerate(train_dl):
# clear the gradients
optimizer.zero_grad()
# compute the model output
yhat = model(inputs)
# calculate loss
loss = criterion(yhat, targets)
# credit assignment
loss.backward()
# update model weights
optimizer.step()
# evaluate the model
def evaluate_model(test_dl, model):
predictions, actuals = list(), list()
for i, (inputs, targets) in enumerate(test_dl):
# evaluate the model on the test set
yhat = model(inputs)
# retrieve numpy array
yhat = yhat.detach().numpy()
actual = targets.numpy()
actual = actual.reshape((len(actual), 1))
# round to class values
yhat = yhat.round()
# store
predictions.append(yhat)
actuals.append(actual)
predictions, actuals = vstack(predictions), vstack(actuals)
# calculate accuracy
acc = accuracy_score(actuals, predictions)
return acc
# make a class prediction for one row of data
def predict(row, model):
# convert row to data
row = Tensor([row])
# make prediction
yhat = model(row)
# retrieve numpy array
yhat = yhat.detach().numpy()
return yhat
# prepare the data
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/ionosphere.csv'
train_dl, test_dl = prepare_data(path)
print(len(train_dl.dataset), len(test_dl.dataset))
# define the network
model = MLP(34)
# train the model
train_model(train_dl, model)
# evaluate the model
acc = evaluate_model(test_dl, model)
print('Accuracy: %.3f' % acc)
# make a single prediction (expect class=1)
row = [1,0,0.99539,-0.05889,0.85243,0.02306,0.83398,-0.37708,1,0.03760,0.85243,-0.17755,0.59755,-0.44945,0.60536,-0.38223,0.84356,-0.38542,0.58212,-0.32192,0.56971,-0.29674,0.36946,-0.47357,0.56811,-0.51171,0.41078,-0.46168,0.21266,-0.34090,0.42267,-0.54487,0.18641,-0.45300]
yhat = predict(row, model)
print('Predicted: %.3f (class=%d)' % (yhat, yhat.round()))
运行该示例首先报告训练和测试数据集的形状,然后拟合模型并在测试数据集上对其进行评估。最后,对单行数据进行预测。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
你得到了什么结果?
能不能换个模式做得更好?
将你的发现发布到下面的评论中。
在这种情况下,我们可以看到模型达到了大约 94%的分类精确率,然后预测一行数据属于类别 1 的概率为 0.99。
235 116
Accuracy: 0.948
Predicted: 0.998 (class=1)
3.2.如何开发多类分类的 MLP
我们将使用鸢尾花多类分类数据集来演示多类分类的 MLP。
这个问题涉及到预测鸢尾花的种类给定的花的措施。
数据集将使用 Pandas 自动下载,但您可以在这里了解更多信息。
鉴于它是一个多类分类,模型必须在输出层为每个类有一个节点,并使用 softmax 激活函数。损失函数是交叉熵,它适用于整数编码的类标签(例如,一个类为 0,下一个类为 1,等等)。).
下面列出了在鸢尾花数据集上拟合和评估 MLP 的完整示例。
# pytorch mlp for multiclass classification
from numpy import vstack
from numpy import argmax
from pandas import read_csv
from sklearn.preprocessing import LabelEncoder
from sklearn.metrics import accuracy_score
from torch import Tensor
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from torch.utils.data import random_split
from torch.nn import Linear
from torch.nn import ReLU
from torch.nn import Softmax
from torch.nn import Module
from torch.optim import SGD
from torch.nn import CrossEntropyLoss
from torch.nn.init import kaiming_uniform_
from torch.nn.init import xavier_uniform_
# dataset definition
class CSVDataset(Dataset):
# load the dataset
def __init__(self, path):
# load the csv file as a dataframe
df = read_csv(path, header=None)
# store the inputs and outputs
self.X = df.values[:, :-1]
self.y = df.values[:, -1]
# ensure input data is floats
self.X = self.X.astype('float32')
# label encode target and ensure the values are floats
self.y = LabelEncoder().fit_transform(self.y)
# number of rows in the dataset
def __len__(self):
return len(self.X)
# get a row at an index
def __getitem__(self, idx):
return [self.X[idx], self.y[idx]]
# get indexes for train and test rows
def get_splits(self, n_test=0.33):
# determine sizes
test_size = round(n_test * len(self.X))
train_size = len(self.X) - test_size
# calculate the split
return random_split(self, [train_size, test_size])
# model definition
class MLP(Module):
# define model elements
def __init__(self, n_inputs):
super(MLP, self).__init__()
# input to first hidden layer
self.hidden1 = Linear(n_inputs, 10)
kaiming_uniform_(self.hidden1.weight, nonlinearity='relu')
self.act1 = ReLU()
# second hidden layer
self.hidden2 = Linear(10, 8)
kaiming_uniform_(self.hidden2.weight, nonlinearity='relu')
self.act2 = ReLU()
# third hidden layer and output
self.hidden3 = Linear(8, 3)
xavier_uniform_(self.hidden3.weight)
self.act3 = Softmax(dim=1)
# forward propagate input
def forward(self, X):
# input to first hidden layer
X = self.hidden1(X)
X = self.act1(X)
# second hidden layer
X = self.hidden2(X)
X = self.act2(X)
# output layer
X = self.hidden3(X)
X = self.act3(X)
return X
# prepare the dataset
def prepare_data(path):
# load the dataset
dataset = CSVDataset(path)
# calculate split
train, test = dataset.get_splits()
# prepare data loaders
train_dl = DataLoader(train, batch_size=32, shuffle=True)
test_dl = DataLoader(test, batch_size=1024, shuffle=False)
return train_dl, test_dl
# train the model
def train_model(train_dl, model):
# define the optimization
criterion = CrossEntropyLoss()
optimizer = SGD(model.parameters(), lr=0.01, momentum=0.9)
# enumerate epochs
for epoch in range(500):
# enumerate mini batches
for i, (inputs, targets) in enumerate(train_dl):
# clear the gradients
optimizer.zero_grad()
# compute the model output
yhat = model(inputs)
# calculate loss
loss = criterion(yhat, targets)
# credit assignment
loss.backward()
# update model weights
optimizer.step()
# evaluate the model
def evaluate_model(test_dl, model):
predictions, actuals = list(), list()
for i, (inputs, targets) in enumerate(test_dl):
# evaluate the model on the test set
yhat = model(inputs)
# retrieve numpy array
yhat = yhat.detach().numpy()
actual = targets.numpy()
# convert to class labels
yhat = argmax(yhat, axis=1)
# reshape for stacking
actual = actual.reshape((len(actual), 1))
yhat = yhat.reshape((len(yhat), 1))
# store
predictions.append(yhat)
actuals.append(actual)
predictions, actuals = vstack(predictions), vstack(actuals)
# calculate accuracy
acc = accuracy_score(actuals, predictions)
return acc
# make a class prediction for one row of data
def predict(row, model):
# convert row to data
row = Tensor([row])
# make prediction
yhat = model(row)
# retrieve numpy array
yhat = yhat.detach().numpy()
return yhat
# prepare the data
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/iris.csv'
train_dl, test_dl = prepare_data(path)
print(len(train_dl.dataset), len(test_dl.dataset))
# define the network
model = MLP(4)
# train the model
train_model(train_dl, model)
# evaluate the model
acc = evaluate_model(test_dl, model)
print('Accuracy: %.3f' % acc)
# make a single prediction
row = [5.1,3.5,1.4,0.2]
yhat = predict(row, model)
print('Predicted: %s (class=%d)' % (yhat, argmax(yhat)))
运行该示例首先报告训练和测试数据集的形状,然后拟合模型并在测试数据集上对其进行评估。最后,对单行数据进行预测。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
你得到了什么结果?
能不能换个型号做得更好?
将你的发现发布到下面的评论中。
在这种情况下,我们可以看到该模型实现了大约 98%的分类准确率,然后预测了一行数据属于每个类的概率,尽管类 0 的概率最高。
100 50
Accuracy: 0.980
Predicted: [[9.5524162e-01 4.4516966e-02 2.4138369e-04]] (class=0)
3.3.如何开发回归 MLP
我们将使用波士顿住房回归数据集来演示用于回归预测建模的 MLP。
这个问题涉及到根据房子和邻居的属性来预测房子的价值。
数据集将使用 Pandas 自动下载,但您可以在这里了解更多信息。
这是一个涉及预测单个数值的回归问题。因此,输出层只有一个节点,并使用默认或线性激活函数(无激活函数)。拟合模型时,均方误差(mse)损失最小。
回想一下,这是回归,不是分类;因此,我们无法计算分类精确率。有关这方面的更多信息,请参见教程:
下面列出了在波士顿住房数据集上拟合和评估 MLP 的完整示例。
# pytorch mlp for regression
from numpy import vstack
from numpy import sqrt
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from torch.utils.data import random_split
from torch import Tensor
from torch.nn import Linear
from torch.nn import Sigmoid
from torch.nn import Module
from torch.optim import SGD
from torch.nn import MSELoss
from torch.nn.init import xavier_uniform_
# dataset definition
class CSVDataset(Dataset):
# load the dataset
def __init__(self, path):
# load the csv file as a dataframe
df = read_csv(path, header=None)
# store the inputs and outputs
self.X = df.values[:, :-1].astype('float32')
self.y = df.values[:, -1].astype('float32')
# ensure target has the right shape
self.y = self.y.reshape((len(self.y), 1))
# number of rows in the dataset
def __len__(self):
return len(self.X)
# get a row at an index
def __getitem__(self, idx):
return [self.X[idx], self.y[idx]]
# get indexes for train and test rows
def get_splits(self, n_test=0.33):
# determine sizes
test_size = round(n_test * len(self.X))
train_size = len(self.X) - test_size
# calculate the split
return random_split(self, [train_size, test_size])
# model definition
class MLP(Module):
# define model elements
def __init__(self, n_inputs):
super(MLP, self).__init__()
# input to first hidden layer
self.hidden1 = Linear(n_inputs, 10)
xavier_uniform_(self.hidden1.weight)
self.act1 = Sigmoid()
# second hidden layer
self.hidden2 = Linear(10, 8)
xavier_uniform_(self.hidden2.weight)
self.act2 = Sigmoid()
# third hidden layer and output
self.hidden3 = Linear(8, 1)
xavier_uniform_(self.hidden3.weight)
# forward propagate input
def forward(self, X):
# input to first hidden layer
X = self.hidden1(X)
X = self.act1(X)
# second hidden layer
X = self.hidden2(X)
X = self.act2(X)
# third hidden layer and output
X = self.hidden3(X)
return X
# prepare the dataset
def prepare_data(path):
# load the dataset
dataset = CSVDataset(path)
# calculate split
train, test = dataset.get_splits()
# prepare data loaders
train_dl = DataLoader(train, batch_size=32, shuffle=True)
test_dl = DataLoader(test, batch_size=1024, shuffle=False)
return train_dl, test_dl
# train the model
def train_model(train_dl, model):
# define the optimization
criterion = MSELoss()
optimizer = SGD(model.parameters(), lr=0.01, momentum=0.9)
# enumerate epochs
for epoch in range(100):
# enumerate mini batches
for i, (inputs, targets) in enumerate(train_dl):
# clear the gradients
optimizer.zero_grad()
# compute the model output
yhat = model(inputs)
# calculate loss
loss = criterion(yhat, targets)
# credit assignment
loss.backward()
# update model weights
optimizer.step()
# evaluate the model
def evaluate_model(test_dl, model):
predictions, actuals = list(), list()
for i, (inputs, targets) in enumerate(test_dl):
# evaluate the model on the test set
yhat = model(inputs)
# retrieve numpy array
yhat = yhat.detach().numpy()
actual = targets.numpy()
actual = actual.reshape((len(actual), 1))
# store
predictions.append(yhat)
actuals.append(actual)
predictions, actuals = vstack(predictions), vstack(actuals)
# calculate mse
mse = mean_squared_error(actuals, predictions)
return mse
# make a class prediction for one row of data
def predict(row, model):
# convert row to data
row = Tensor([row])
# make prediction
yhat = model(row)
# retrieve numpy array
yhat = yhat.detach().numpy()
return yhat
# prepare the data
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
train_dl, test_dl = prepare_data(path)
print(len(train_dl.dataset), len(test_dl.dataset))
# define the network
model = MLP(13)
# train the model
train_model(train_dl, model)
# evaluate the model
mse = evaluate_model(test_dl, model)
print('MSE: %.3f, RMSE: %.3f' % (mse, sqrt(mse)))
# make a single prediction (expect class=1)
row = [0.00632,18.00,2.310,0,0.5380,6.5750,65.20,4.0900,1,296.0,15.30,396.90,4.98]
yhat = predict(row, model)
print('Predicted: %.3f' % yhat)
运行该示例首先报告训练和测试数据集的形状,然后拟合模型并在测试数据集上对其进行评估。最后,对单行数据进行预测。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
你得到了什么结果?
能不能换个型号做得更好?
将你的发现发布到下面的评论中。
在这种情况下,我们可以看到模型实现了大约 82 的 MSE,这是大约 9 的 RMSE(单位是千美元)。然后为单个示例预测值 21。
339 167
MSE: 82.576, RMSE: 9.087
Predicted: 21.909
3.4.如何开发一个用于图像分类的有线电视网络
卷积神经网络,简称 CNNs,是一种为图像输入而设计的网络。
它们由带有提取特征(称为特征图)的卷积层和提取特征到最显著元素的汇集层的模型组成。
中枢神经系统最适合图像分类任务,尽管它们可以用于以图像为输入的各种任务。
一个流行的图像分类任务是 MNIST 手写数字分类。它涉及成千上万的手写数字,这些数字必须被归类为 0 到 9 之间的数字。
torchvision API 提供了一个方便的函数来直接下载和加载这个数据集。
以下示例加载数据集并绘制前几幅图像。
# load mnist dataset in pytorch
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST
from torchvision.transforms import Compose
from torchvision.transforms import ToTensor
from matplotlib import pyplot
# define location to save or load the dataset
path = '~/.torch/datasets/mnist'
# define the transforms to apply to the data
trans = Compose([ToTensor()])
# download and define the datasets
train = MNIST(path, train=True, download=True, transform=trans)
test = MNIST(path, train=False, download=True, transform=trans)
# define how to enumerate the datasets
train_dl = DataLoader(train, batch_size=32, shuffle=True)
test_dl = DataLoader(test, batch_size=32, shuffle=True)
# get one batch of images
i, (inputs, targets) = next(enumerate(train_dl))
# plot some images
for i in range(25):
# define subplot
pyplot.subplot(5, 5, i+1)
# plot raw pixel data
pyplot.imshow(inputs[i][0], cmap='gray')
# show the figure
pyplot.show()
运行该示例会加载 MNIST 数据集,然后汇总默认的训练和测试数据集。
Train: X=(60000, 28, 28), y=(60000,)
Test: X=(10000, 28, 28), y=(10000,)
然后创建一个图,显示训练数据集中手写图像示例的网格。

来自 MNIST 数据集的手写数字图
我们可以训练一个 CNN 模型来对 MNIST 数据集中的图像进行分类。
请注意,图像是灰度像素数据的数组,因此,我们必须在数据中添加通道维度,然后才能将图像用作模型的输入。
最好将像素值从默认范围 0-255 缩放到均值为零、标准差为 1。有关缩放像素值的更多信息,请参见教程:
下面列出了在 MNIST 数据集上拟合和评估 CNN 模型的完整示例。
# pytorch cnn for multiclass classification
from numpy import vstack
from numpy import argmax
from pandas import read_csv
from sklearn.metrics import accuracy_score
from torchvision.datasets import MNIST
from torchvision.transforms import Compose
from torchvision.transforms import ToTensor
from torchvision.transforms import Normalize
from torch.utils.data import DataLoader
from torch.nn import Conv2d
from torch.nn import MaxPool2d
from torch.nn import Linear
from torch.nn import ReLU
from torch.nn import Softmax
from torch.nn import Module
from torch.optim import SGD
from torch.nn import CrossEntropyLoss
from torch.nn.init import kaiming_uniform_
from torch.nn.init import xavier_uniform_
# model definition
class CNN(Module):
# define model elements
def __init__(self, n_channels):
super(CNN, self).__init__()
# input to first hidden layer
self.hidden1 = Conv2d(n_channels, 32, (3,3))
kaiming_uniform_(self.hidden1.weight, nonlinearity='relu')
self.act1 = ReLU()
# first pooling layer
self.pool1 = MaxPool2d((2,2), stride=(2,2))
# second hidden layer
self.hidden2 = Conv2d(32, 32, (3,3))
kaiming_uniform_(self.hidden2.weight, nonlinearity='relu')
self.act2 = ReLU()
# second pooling layer
self.pool2 = MaxPool2d((2,2), stride=(2,2))
# fully connected layer
self.hidden3 = Linear(5*5*32, 100)
kaiming_uniform_(self.hidden3.weight, nonlinearity='relu')
self.act3 = ReLU()
# output layer
self.hidden4 = Linear(100, 10)
xavier_uniform_(self.hidden4.weight)
self.act4 = Softmax(dim=1)
# forward propagate input
def forward(self, X):
# input to first hidden layer
X = self.hidden1(X)
X = self.act1(X)
X = self.pool1(X)
# second hidden layer
X = self.hidden2(X)
X = self.act2(X)
X = self.pool2(X)
# flatten
X = X.view(-1, 4*4*50)
# third hidden layer
X = self.hidden3(X)
X = self.act3(X)
# output layer
X = self.hidden4(X)
X = self.act4(X)
return X
# prepare the dataset
def prepare_data(path):
# define standardization
trans = Compose([ToTensor(), Normalize((0.1307,), (0.3081,))])
# load dataset
train = MNIST(path, train=True, download=True, transform=trans)
test = MNIST(path, train=False, download=True, transform=trans)
# prepare data loaders
train_dl = DataLoader(train, batch_size=64, shuffle=True)
test_dl = DataLoader(test, batch_size=1024, shuffle=False)
return train_dl, test_dl
# train the model
def train_model(train_dl, model):
# define the optimization
criterion = CrossEntropyLoss()
optimizer = SGD(model.parameters(), lr=0.01, momentum=0.9)
# enumerate epochs
for epoch in range(10):
# enumerate mini batches
for i, (inputs, targets) in enumerate(train_dl):
# clear the gradients
optimizer.zero_grad()
# compute the model output
yhat = model(inputs)
# calculate loss
loss = criterion(yhat, targets)
# credit assignment
loss.backward()
# update model weights
optimizer.step()
# evaluate the model
def evaluate_model(test_dl, model):
predictions, actuals = list(), list()
for i, (inputs, targets) in enumerate(test_dl):
# evaluate the model on the test set
yhat = model(inputs)
# retrieve numpy array
yhat = yhat.detach().numpy()
actual = targets.numpy()
# convert to class labels
yhat = argmax(yhat, axis=1)
# reshape for stacking
actual = actual.reshape((len(actual), 1))
yhat = yhat.reshape((len(yhat), 1))
# store
predictions.append(yhat)
actuals.append(actual)
predictions, actuals = vstack(predictions), vstack(actuals)
# calculate accuracy
acc = accuracy_score(actuals, predictions)
return acc
# prepare the data
path = '~/.torch/datasets/mnist'
train_dl, test_dl = prepare_data(path)
print(len(train_dl.dataset), len(test_dl.dataset))
# define the network
model = CNN(1)
# # train the model
train_model(train_dl, model)
# evaluate the model
acc = evaluate_model(test_dl, model)
print('Accuracy: %.3f' % acc)
运行该示例首先报告训练和测试数据集的形状,然后拟合模型并在测试数据集上对其进行评估。
注:考虑到算法或评估程序的随机性,或数值精确率的差异,您的结果可能会有所不同。考虑运行该示例几次,并比较平均结果。
你得到了什么结果?
能不能换个型号做得更好?
将你的发现发布到下面的评论中。
在这种情况下,我们可以看到该模型在测试数据集上实现了大约 98%的分类准确率。然后我们可以看到,模型为训练集中的第一幅图像预测了类别 5。
60000 10000
Accuracy: 0.985
进一步阅读
如果您想更深入地了解这个主题,本节将提供更多资源。
书
- 深度学习,2016 年。
- 为深度学习编程 PyTorch:创建和部署深度学习应用程序,2018。
- 用 PyTorch 深度学习,2020。
- 带 fastai 和 PyTorch 的程序员深度学习:没有博士学位的 ai 应用,2020。
PyTorch 项目
- PyTorch 主页。
- PyTorch 文件
- pytorch 安装指南
- 问号,维基百科。
- 在 GitHub 上的 pytorch。
蜜蜂
摘要
在本教程中,您发现了一个在 PyTorch 中开发深度学习模型的分步指南。
具体来说,您了解到:
- Torch 和 PyTorch 的区别以及如何安装和确认 PyTorch 工作正常。
- PyTorch 模型的五步生命周期以及如何定义、拟合和评估模型。
- 如何为回归、分类和预测建模任务开发 PyTorch 深度学习模型?
你有什么问题吗?
在下面的评论中提问,我会尽力回答。
























 5398
5398

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








