Machine Learning Mastery LSTM 教程（五）

于 2024-09-16 12:01:10 发布
阅读量1.6k 收藏 29
点赞数 11
分类专栏： MLM 文章标签： MLM
License CC BY-NC-SA 4.0 / 自豪地采用谷歌翻译
本文链接：https://blog.csdn.net/wizardforcel/article/details/142301028
版权

原文：Machine Learning Mastery

协议：CC BY-NC-SA 4.0

基于循环神经网络的序列预测模型的简要介绍

原文： machinelearningmastery.com/models-sequence-prediction-recurrent-neural-networks/

序列预测是涉及使用历史序列信息来预测序列中的下一个或多个值的问题。

序列可以是符号，如句子中的字母，也可以是价格时间序列中的实际值。在时间序列预测的背景下，序列预测可能是最容易理解的，因为问题已经被普遍理解。

在这篇文章中，您将发现可用于构建自己的序列预测问题的标准序列预测模型。

阅读这篇文章后，你会知道：

  • 如何使用循环神经网络对序列预测问题进行建模。
  • 循环神经网络使用的 4 种标准序列预测模型。
  • 在应用序列预测模型时，初学者所犯的两个最常见的误解。

让我们开始吧。

教程概述

本教程分为 4 个部分;他们是：

  1. 循环神经网络序列预测
  2. 序列预测模型
  3. 来自 Timesteps 的基数不是特征
  4. 从业者的两个常见误解

循环神经网络序列预测

循环神经网络，如长短期记忆（LSTM）网络，是为序列预测问题而设计的。

实际上，在撰写本文时，LSTM 在具有挑战性的序列预测问题（例如神经机器翻译（将英语翻译成法语））中实现了最先进的结果。

LSTM 通过学习将输入序列值（X）映射到输出序列值（y）的函数（f（…））来工作。

y(t) = f(X(t))

学习的映射函数是静态的，可以被认为是一个获取输入变量并使用内部变量的程序。内部变量由网络维护的内部状态表示，并在输入序列中的每个值上建立或累积。

… RNN 将输入向量与其状态向量与固定（但已学习）函数组合以产生新的状态向量。在编程术语中，这可以解释为运行具有某些输入和一些内部变量的固定程序。

可以使用不同数量的输入或输出来定义静态映射函数，我们将在下一节中进行讨论。

序列预测模型

在本节中，将回顾序列预测的 4 个主要模型。

我们将使用以下术语：

  • X：输入序列值可以由时间步长界定，例如， X（1）。
  • u：隐藏状态值可以由时间步长界定，例如 U（1）。
  • y：输出序列值可以由时间步长界定，例如， Y（1）。

一对一模型

一对一模型为每个输入值生成一个输出值。

One-to-One Sequence Prediction Model

一对一序列预测模型

第一步的内部状态为零;从那时起，内部状态在前一时间步骤累积。

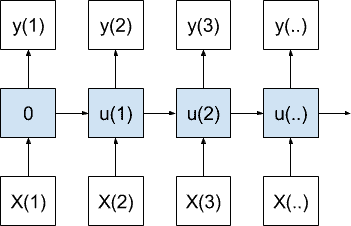
One-to-One Sequence Prediction Model Over Time

随时间变化的一对一序列预测模型

在序列预测的情况下，该模型将针对作为输入接收的每个观察时间步长产生一个时间步长预测。

这对 RNN 的使用很差，因为模型没有机会学习输入或输出时间步长（例如 BPTT ）。如果您发现为序列预测实现此模型，您可能打算使用多对一模型。

一对多模型

一对多模型为一个输入值生成多个输出值。

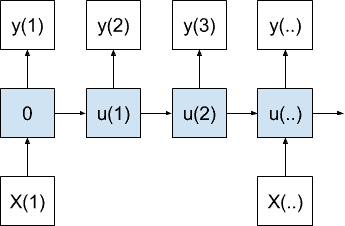
One-to-Many Sequence Prediction Model

一对多序列预测模型

当产生输出序列中的每个值时，累积内部状态。

该模型可用于图像字幕，其中一个图像被提供作为输入并且一系列单词被生成为输出。

多对一模型

多对一模型在接收到多个输入值后生成一个输出值。

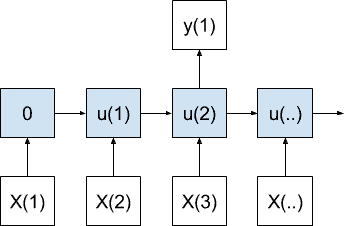
Many-to-One Sequence Prediction Model

多对一序列预测模型

在产生最终输出值之前，内部状态与每个输入值累加。

在时间序列的情况下，该模型将使用一系列最近的观察来预测下一个时间步。该架构将代表经典的自回归时间序列模型。

多对多模型

多对多模型在接收到多个输入值后会产生多个输出。

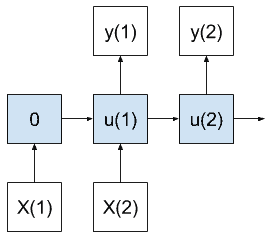
Many-to-Many Sequence Prediction Model

多对多序列预测模型

与多对一情况一样，累积状态直到创建第一个输出，但在这种情况下输出多个时间步长。

重要的是，输入时间步数不必与输出时间步数相匹配。考虑以不同速率运行的输入和输出时间步长。

在时间序列预测的情况下，该模型将使用一系列最近的观测来进行多步预测。

从某种意义上说，它结合了多对一和一对多模型的功能。

来自 Timesteps 的基数（不是特色！）

常见的混淆点是将上述序列映射模型的示例与多个输入和输出特征混淆。

序列可以由单个值组成，每个时间步长一个。

或者，序列可以很容易地表示在时间步骤的多个观察的向量。时间步长的向量中的每个项可以被认为是其自己的单独时间序列。它不会影响上述模型的描述。

例如，将温度和压力的一个时间步长作为输入并且预测温度和压力的一个时间步长的模型是一对一模型，而不是多对多模型。

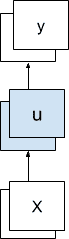
Multiple-Feature Sequence Prediction Model

多特征序列预测模型

该模型确实将两个值作为输入并预测两个值，但是只有一个序列时间步长表示输入并预测为输出。

上面定义的序列预测模型的基数是指时间步骤，而不是特征（例如，单变量或多变量序列）。

从业者的两个常见误解

在从业者实现循环神经网络时，特征与时间步骤的混淆会导致两个主要的误解：

1.作为输入功能的时间步长

先前时间步的观察被构造为模型的输入特征。

这是输入多层感知机使用的序列预测问题的经典的基于固定窗口的方法。相反，序列应该一次一步地进给。

这种混淆可能会导致您认为您已经实现了多对一或多对多序列预测模型，而实际上您只有一个时间步的单个向量输入。

2.作为输出特征的时间步长

多个未来时间步骤的预测被构造为模型的输出特征。

这是多层感知机和其他机器学习算法使用的多步预测的经典固定窗口方法。相反，序列预测应该一次一步地生成。

这种混淆可能会导致您认为您已经实现了一对多或多对多的序列预测模型，而实际上您只有一个时间步的单个向量输出（例如 seq2vec 而不是 seq2seq）。

注意：将时间步长作为序列预测问题中的特征构建是一种有效的策略，即使使用循环神经网络也可以提高表现（尝试一下！）。这里的重点是了解常见的陷阱，而不是在构建自己的预测问题时欺骗自己。

进一步阅读

如果您要深入了解，本节将提供有关该主题的更多资源。

摘要

在本教程中，您发现了使用循环神经网络进行序列预测的标准模型。

具体来说，你学到了：

  • 如何使用循环神经网络对序列预测问题进行建模。
  • 循环神经网络使用的 4 种标准序列预测模型。
  • 在应用序列预测模型时，初学者所犯的两个最常见的误解。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

深度学习的循环神经网络算法之旅

原文： machinelearningmastery.com/recurrent-neural-network-algorithms-for-deep-learning/

循环神经网络（RNN）是一种人工神经网络，其向网络添加额外的权重以在网络图中创建循环以努力维持内部状态。

向神经网络添加状态的承诺是，他们将能够明确地学习和利用序列预测问题中的上下文，例如订单或时间组件的问题。

在这篇文章中，您将参观用于深度学习的循环神经网络。

阅读这篇文章后，你会知道：

  • 顶级循环神经网络如何用于深度学习，例如 LSTM，GRU 和 NTM。
  • 顶级 RNN 如何与人工神经网络中更广泛的复发研究相关。
  • 对 RNN 的研究如何在一系列具有挑战性的问题上取得了最先进的表现。

请注意，我们不会涵盖所有可能的循环神经网络。相反，我们将关注用于深度学习的循环神经网络（LSTM，GRU 和 NTM）以及理解它们所需的上下文。

让我们开始吧。

A Tour of Recurrent Neural Network Algorithms for Deep Learning

深度学习的循环神经网络算法之旅
照片由 Santiago Medem 拍摄，保留一些权利。

概观

我们将从为循环神经网络领域设置场景开始。

接下来，我们将深入研究用于深度学习的 LSTM，GRU 和 NTM。

然后，我们将花一些时间在与使用 RNN 进行深度学习相关的高级主题上。

  • 循环神经网络
    • 完全经常性网络
    • 循环神经网络
    • 神经历史压缩机
  • 长期短期记忆网络
  • 门控递归单元神经网络
  • 神经图灵机

循环神经网络

让我们设置场景。

流行的观点表明，重复会给网络拓扑带来内存。

考虑这一点的更好方法是训练集包含带有当前训练示例的一组输入的示例。这是“常规的，例如传统的多层感知机。

X(i) -> y(i)

但是训练示例补充了前一个示例中的一组输入。这是“非常规的”，例如循环神经网络。

[X(i-1), X(i)] -> y(i)

与所有前馈网络范例一样，问题是如何将输入层连接到输出层，包括反馈激活，然后训练构造以收敛。

现在让我们来看看不同类型的循环神经网络，从非常简单的概念开始。

完全经常性网络

多层感知机的分层拓扑被保留，但每个元素都与架构中的每个其他元素具有加权连接，​​并且与其自身具有单个反馈连接。

并非所有连接都经过训练，并且误差导数的极端非线性意味着传统的反向传播将不起作用，因此采用时间反向传播接近或随机梯度下降。

另请参阅 Bill Wilson 的 Tensor 产品网络（1991）。

循环神经网络

循环神经网络是递归网络的线性架构变体。

递归促进了分层特征空间中的分支，并且随着训练的进行，所得到的网络架构模仿了这一点。

使用梯度下降通过子梯度方法实现训练。

这在 R. Socher 等人， Parsing Natural Scenes and Natural Language with Recursive Neural Networks ，2011 中有详细描述。

神经历史压缩机

Schmidhuber 在 1991 年首次报告了一个非常深入的学习器，他能够通过无人监督的 RNN 层次结构预训练，对数百个神经层进行信用分配。

每个 RNN 都经过无人监督训练，以预测下一个输入。然后，仅向前馈送生成错误的输入，将新信息传送到层级中的下一个 RNN，然后以较慢的自组织时间尺度处理。

结果表明，没有信息丢失，只是压缩了。 RNN 栈是数据的“深层生成模型”。可以从压缩形式重建数据。

参见 J. Schmidhuber 等人，神经网络中的深度学习：概述，2014。

随着误差通过大拓扑向后传播，非线性导数的极值计算增加，反向传播失败，即使不是不可能，信用分配也很困难。

长期短期记忆网络

对于传统的反向传播时间（BPTT）或实时循环学习（RTTL），在时间上向后流动的误差信号往往会爆炸或消失。

反向传播误差的时间演变指数地取决于权重的大小。重量爆炸可能导致重量振荡，而在消失导致学习弥合长时间滞后并花费大量时间，或根本不起作用。

  • LSTM 是一种新颖的循环网络架构训练，具有适当的基于梯度的学习算法。
  • LSTM 旨在克服错误回流问题。它可以学习桥接超过 1000 步的时间间隔。
  • 这在存在嘈杂，不可压缩的输入序列时是真实的，而不会损失短时滞能力。

错误的回流问题通过一种有效的基于梯度的算法克服，该算法用于通过特殊单元的内部状态执行常量（因此既不爆炸也不消失）的错误流。这些单位减少了“输入权重冲突”和“输出权重冲突”的影响。

输入权重冲突：如果输入非零，则必须使用相同的输入权重来存储某些输入并忽略其他输入，然后通常会收到相互冲突的权重更新信号。

这些信号将尝试使重量参与存储输入和保护输入。这种冲突使得学习变得困难，并且需要更多上下文敏感的机制来通过输入权重来控制“写入操作”。

输出权重冲突：只要单元的输出不为零，来自该单元的输出连接的权重将吸引在序列处理期间产生的冲突的权重更新信号。

这些信号将试图使输出权重参与访问存储在处理单元中的信息，并且在不同时间保护后续单元不被正向馈送的单元的输出扰动。

这些冲突并非特定于长期滞后，同样会影响短期滞后。值得注意的是，随着滞后增加，必须保护存储的信息免受扰动，特别是在学习的高级阶段。

网络架构：不同类型的单元可以传达有关网络当前状态的有用信息。例如，输入门（输出门）可以使用来自其他存储器单元的输入来决定是否在其存储器单元中存储（访问）某些信息。

存储器单元包含门。盖茨特定于他们调解的联系。输入门用于补救输入权重冲突，而输出门工作则消除输出权重冲突。

门：具体来说，为了减轻输入和输出权重冲突和扰动，引入了乘法输入门单元，以保护存储内容免受无关输入的干扰，乘法输出门单元保护其他单元免受扰动通过当前无关的存储内容存储。

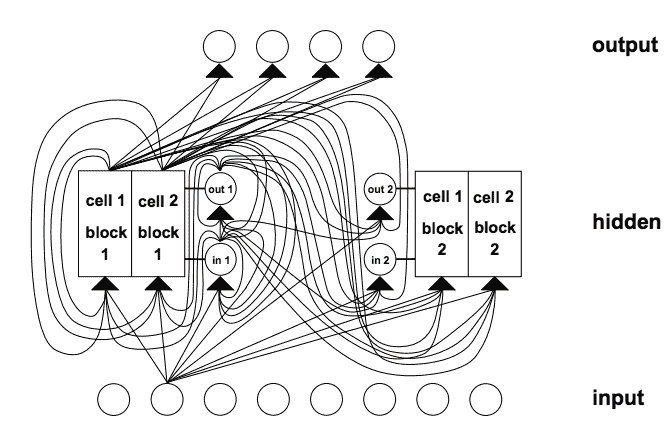
Example of LSTM Architecture

具有 8 个输入单元，4 个输出单元和 2 个大小为 2. in1 的存储器单元块的 LSTM 网络的示例标记输入门，out1 标记输出门，并且 cell1 = block1 标记块 1 的第一存储器单元。
摘自 1997 年的长短记忆。

与多层感知机相比，LSTM 中的连接性是复杂的，因为处理元件的多样性和反馈连接的包含。

存储器单元块：共享相同输入门和相同输出门的存储器单元形成称为“存储器单元块”的结构。

存储单元块便于信息存储;与传统神经网络一样，在单个单元内编码分布式输入并不容易。大小为 1 的存储器单元块只是一个简单的存储器单元。

学习：实时循环学习（RTRL）的一种变体，它考虑了由输入和输出门引起的改变的乘法动力学，用于确保通过内存状态存储单元错误传播的非衰减误差到达“存储器单元网络输入”不会及时传播回来。

猜测：这种随机方法可以胜过许多术语滞后算法。已经确定，通过简单的随机权重猜测可以比通过所提出的算法更快地解决在先前工作中使用的许多长时滞后任务。

参见 S.Hochreiter 和 J. Schmidhuber， Long-Short Term Memory ，1997。

LSTM 循环神经网络最有趣的应用是语言处理工作。有关全面的描述，请参阅 Gers 的工作。

  • F. Gers 和 J. Schmidhuber， LSTM Recurrent Networks 学习简单的上下文无关和上下文敏感语言，2001。
  • F. Gers，循环神经网络中的长短期记忆，博士。论文，2001 年。

LSTM 限制

LSTM 的高效截断版本不会轻易解决类似“强烈延迟 XOR”的问题。

每个存储器单元块需要输入门和输出门。在其他经常性方法中没有必要。

通过存储器单元内的“恒定误差卡鲁塞尔”的恒定误差流产生与一次呈现整个输入串的传统前馈架构相同的效果。

与其他前馈方法一样，LSTM 与“摄政”概念一样存在缺陷。如果需要精确计数时间步长，则可能需要额外的计数机制。

LSTM 的优点

算法弥合长时间滞后的能力是架构内存单元中持续误差反向传播的结果。

LSTM 可以近似噪声问题域，分布式表示和连续值。

LSTM 很好地概括了所考虑的问题域。这很重要，因为某些任务对于已经建立的循环网络来说是难以处理的。

在问题域上对网络参数进行微调似乎是不必要的。

就每个权重和时间步骤的更新复杂性而言，LSTM 基本上等同于 BPTT。

LSTM 显示出强大功能，在机器翻译等领域实现了最先进的结果。

门控递归单元神经网络

门控循环神经网络已成功应用于顺序或时间数据。

最适合语音识别，自然语言处理和机器翻译，与 LSTM 一起，它们在长序列问题域中表现良好。

在 LSTM 主题中考虑了门控，并且涉及门控网络生成信号，该信号用于控制当前输入和先前存储器如何工作以更新当前激活，从而控制当前网络状态。

在整个学习阶段，门自身被加权并根据算法选择性地更新。

门网络以增加的复杂性的形式引入了额外的计算开销，因此增加了参数化。

LSTM RNN 架构使用简单 RNN 的计算作为内部存储器单元（状态）的中间候选者。门控递归单元（GRU）RNN 将门控信号从 LSTM RNN 模型减少到两个。两个门被称为更新门和复位门。

GRU（和 LSTM）RNN 中的选通机制在参数化方面是简单 RNN 的复制品。对应于这些门的权重也使用 BPTT 随机梯度下降来更新，因为它试图使成本函数最小化。

每个参数更新将涉及与整个网络的状态有关的信息。这可能会产生不利影响。

门控的概念进一步探索并扩展了三种新的变量门控机制。
已经考虑的三个门控变量是 GRU1，其中每个门仅使用先前的隐藏状态和偏差来计算; GRU2，其中每个门仅使用先前的隐藏状态计算;和 GRU3，其中每个门仅使用偏差计算。使用 GRU3 观察到参数的显着减少，产生最小数量。

使用来自手写数字的 MNIST 数据库和 IMDB 电影评论数据集的数据对三种变体和 GRU RNN 进行基准测试。

从 MNIST 数据集生成两个序列长度，并且从 IMDB 数据集生成一个序列长度。

门的主要驱动信号似乎是（周期性）状态，因为它包含有关其他信号的基本信息。

随机梯度下降的使用隐含地携带关于网络状态的信息。这可以解释在门信号中单独使用偏置的相对成功，因为其自适应更新携带关于网络状态的信息。

门控变体通过有限的拓扑评估来探索门控的机制。

有关更多信息，请参阅

神经图灵机

神经图灵机通过将它们耦合到外部存储器资源来扩展神经网络的能力，它们可以通过注意过程与之交互。

组合系统类似于图灵机或冯·诺依曼架构，但是端到端是可区分的，允许它通过梯度下降进行有效训练。

初步结果表明，神经图灵机可以推断出简单的算法，例如输入和输出示例中的复制，排序和关联召回。

RNN 在其他机器学习方法中脱颖而出，因为它们能够在长时间内学习和执行复杂的数据转换。此外，众所周知，RNN 是图灵完备的，因此如果连接正确，则具有模拟任意过程的能力。

扩展了标准 RNN 的功能，以简化算法任务的解决方案。这种丰富主要是通过一个大的，可寻址的存储器，因此，类似于图灵通过无限记忆磁带丰富有限状态机，并被称为“神经图灵机”（NTM）。

与图灵机不同，NTM 是一种可区分的计算机，可以通过梯度下降进行训练，从而为学习程序提供实用的机制。

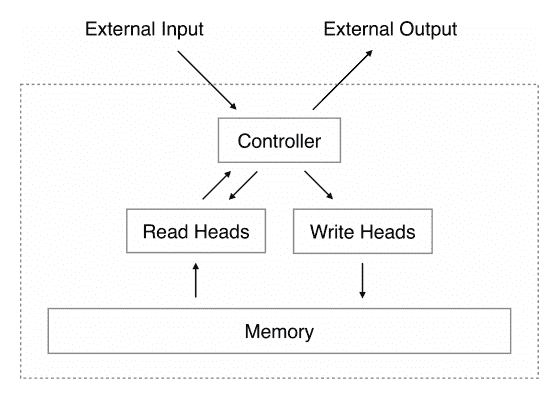
Neural Turing Machine Architecture

NTM Architecture 通常如上所示。在每个更新周期期间，控制器网络接收来自外部环境的输入并作为响应发出输出。它还通过一组并行读写磁头读取和写入存储器矩阵。虚线表示 NTM 电路与外界之间的划分。
摘自神经图灵机，2014 年。

至关重要的是，该建筑的每个组成部分都是可区分的，因此可以直接用梯度下降进行训练。这是通过定义“模糊”读写操作来实现的，这些操作与存储器中的所有元素或多或少地相互作用（而不是像普通的图灵机或数字计算机那样寻址单个元素）。

For more information see:

NTM 实验

复制任务测试 NTM 是否可以存储和调用一长串任意信息。向网络呈现随机二进制向量的输入序列，后跟定界符标志。

训练网络以复制 8 位随机向量的序列，其中序列长度在 1 和 20 之间随机化。目标序列只是输入序列的副本（没有定界符号）。

重复复制任务通过要求网络将复制的序列输出指定的次数然后发出序列结束标记来扩展复制。主要动机是看 NTM 是否可以学习一个简单的嵌套函数。

网络接收随机二进制向量的随机长度序列，随后是指示所需拷贝数的标量值，其出现在单独的输入通道上。

关联召回任务涉及组织由“间接”引起的数据，即当一个数据项指向另一个时。构造项目列表以便查询其中一个项目要求网络返回后续项目。

定义了由分隔符符号左右界定的二进制向量序列。在将多个项目传播到网络之后，通过显示随机项目来查询网络，并查看网络是否可以生成下一个项目。

动态 N-Grams 任务测试 NTM 是否可以通过使用内存作为可重写表来快速适应新的预测分布，它可以用来保持转换统计的计数，从而模拟传统的 N-Gram 模型。

考虑二进制序列上所有可能的 6-Gram 分布的集合。每个 6-Gram 分布可以表示为 32 个数字的表，指定下一个比特为 1 的概率，给定所有可能的长度为 5 的二进制历史。通过使用当前查找表绘制 200 个连续位来生成特定训练序列。网络一次一位地观察序列，然后被要求预测下一位。

优先级排序任务测试 NTM 的排序能力。随机二进制向量序列与每个向量的标量优先级一起输入到网络。优先级从[-1,1]范围内均匀绘制。目标序列包含根据其优先级排序的二元向量。

NTM 将 LSTM 的前馈架构作为其组件之一。

摘要

在这篇文章中，您发现了用于深度学习的循环神经网络。

具体来说，你学到了：

  • 顶级循环神经网络如何用于深度学习，例如 LSTM，GRU 和 NTM。
  • 顶级 RNN 如何与人工神经网络中更广泛的复发研究相关。
  • RNN 的研究如何在一系列具有挑战性的问题上实现最先进的表现。

这是一个很重要的帖子。

您对深度学习的 RNN 有任何疑问吗？
在下面的评论中提出您的问题，我会尽力回答。

如何重塑 Keras 长短期记忆网络的输入数据

原文：https://machinelearningmastery.com/reshape-input-data-long-short-term-memory-networks-keras/

最后更新于 2019 年 8 月 14 日

很难理解如何准备序列数据输入 LSTM 模型。

通常，对于如何定义 LSTM 模型的输入层存在困惑。

对于如何将可能是 1D 或 2D 数字矩阵的序列数据转换为 LSTM 输入图层所需的 3D 格式，也存在困惑。

在本教程中，您将了解如何定义 LSTM 模型的输入图层，以及如何为 LSTM 模型重塑加载的输入数据。

完成本教程后，您将知道:

  • 如何定义 LSTM 输入层。
  • 如何为 LSTM 模型重塑一维序列数据并定义输入图层。
  • 如何为 LSTM 模型重塑多个并行系列数据并定义输入图层。

用我的新书Python 的长短期记忆网络启动你的项目，包括循序渐进教程和所有示例的 Python 源代码文件。

我们开始吧。

How to Reshape Input for Long Short-Term Memory Networks in Keras

如何在 Keras 重塑长短期记忆网络的输入
图片由全球景观论坛提供，保留部分权利。

教程概述

本教程分为 4 个部分；它们是:

  1. LSTM 输入层
  2. 具有单输入样本的 LSTM 示例
  3. 具有多种输入功能的 LSTM 示例
  4. LSTM 输入提示

LSTM 输入层

LSTM 输入层由网络第一个隐藏层上的“ input_shape ”参数指定。

这可能会让初学者感到困惑。

例如，下面是具有一个隐藏 LSTM 层和一个密集输出层的网络示例。

model = Sequential()
model.add(LSTM(32))
model.add(Dense(1))

在本例中，LSTM()图层必须指定输入的形状。

每个 LSTM 层的输入必须是三维的。

这种输入的三个维度是:

  • 样品。一个序列就是一个样本。一批由一个或多个样品组成。
  • 时间步长。一个时间步长是样本中的一个观察点。
  • 功能。一个特点是一步一个观察。

这意味着，在拟合模型和进行预测时，输入图层需要一个三维数据阵列，即使阵列的特定维度包含单个值，例如一个样本或一个特征。

定义 LSTM 网络的输入图层时，网络假设您有 1 个或更多样本，并要求您指定时间步长数和要素数。您可以通过为“ input_shape ”参数指定一个元组来实现这一点。

例如，下面的模型定义了一个需要 1 个或更多样本、50 个时间步长和 2 个特征的输入层。

model = Sequential()
model.add(LSTM(32, input_shape=(50, 2)))
model.add(Dense(1))

既然我们已经知道了如何定义 LSTM 输入图层和对 3D 输入的期望，那么让我们来看一些如何为 LSTM 准备数据的示例。

单输入样本的 LSTM 示例

考虑这样的情况:您有一个由多个时间步骤组成的序列和一个特性。

例如，这可能是 10 个值的序列:

0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0

我们可以将这个数字序列定义为一个 NumPy 数组。

from numpy import array
data = array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0])

然后，我们可以在 NumPy 数组上使用*重塑()*函数，将这个一维数组重塑为一个三维数组，每个时间步长有 1 个样本、10 个时间步长和 1 个特征。

当在数组上调用时，*重塑()*函数接受一个参数，该参数是定义数组新形状的元组。我们不能传入任何一组数字；整形必须均匀地重新组织数组中的数据。

data = data.reshape((1, 10, 1))

一旦重塑，我们就可以打印新的阵列形状。

print(data.shape)

将所有这些放在一起，下面列出了完整的示例。

from numpy import array
data = array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0])
data = data.reshape((1, 10, 1))
print(data.shape)

运行该示例将打印单个样本的新三维形状。

(1, 10, 1)

该数据现在可以用作输入( X )到输入形状为(10，1)的 LSTM。

model = Sequential()
model.add(LSTM(32, input_shape=(10, 1)))
model.add(Dense(1))

具有多种输入功能的 LSTM 示例

考虑有多个并行系列作为模型输入的情况。

例如，这可能是由 10 个值组成的两个并行系列:

series 1: 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0
series 2: 1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1

我们可以将这些数据定义为 2 列 10 行的矩阵:

from numpy import array
data = array([
	[0.1, 1.0],
	[0.2, 0.9],
	[0.3, 0.8],
	[0.4, 0.7],
	[0.5, 0.6],
	[0.6, 0.5],
	[0.7, 0.4],
	[0.8, 0.3],
	[0.9, 0.2],
	[1.0, 0.1]])

该数据可以被构建为具有 10 个时间步长和 2 个特征的 1 个样本。

它可以按如下方式重新造型为三维阵列:

data = data.reshape(1, 10, 2)

将所有这些放在一起，下面列出了完整的示例。

from numpy import array
data = array([
	[0.1, 1.0],
	[0.2, 0.9],
	[0.3, 0.8],
	[0.4, 0.7],
	[0.5, 0.6],
	[0.6, 0.5],
	[0.7, 0.4],
	[0.8, 0.3],
	[0.9, 0.2],
	[1.0, 0.1]])
data = data.reshape(1, 10, 2)
print(data.shape)

运行该示例将打印单个样本的新三维形状。

(1, 10, 2)

该数据现在可以用作输入( X )到输入形状为(10，2)的 LSTM。

model = Sequential()
model.add(LSTM(32, input_shape=(10, 2)))
model.add(Dense(1))

工作时间更长的示例

有关准备数据的完整端到端工作示例，请参见本文:

LSTM 输入提示

本节列出了一些提示，可以帮助您准备 LSTMs 的输入数据。

  • LSTM 输入图层必须是 3D 的。
  • 3 个输入维度的含义是:样本、时间步长和特征。
  • LSTM 输入图层由第一个隐藏图层上的输入形状参数定义。
  • input_shape 参数采用两个值的元组来定义时间步长和特征的数量。
  • 假设样本数为 1 或更多。
  • NumPy 阵列上的*重塑()*功能可用于将 1D 或 2D 数据重塑为 3D。
  • *重塑()*函数将元组作为定义新形状的参数。

进一步阅读

如果您想了解更多信息，本节将提供更多相关资源。

摘要

在本教程中，您发现了如何为 LSTMs 定义输入图层，以及如何重塑序列数据以输入到 LSTMs。

具体来说，您了解到:

  • 如何定义 LSTM 输入层。
  • 如何为 LSTM 模型重塑一维序列数据并定义输入图层。
  • 如何为 LSTM 模型重塑多个并行系列数据并定义输入图层。

你有什么问题吗？
在下面的评论中提问，我会尽力回答。

如何在 Keras 中重塑长短期存储网络的输入数据

原文： machinelearningmastery.com/reshape-in​​put-data-long-short-term-memory-networks-keras/

可能很难理解如何准备序列数据以输入 LSTM 模型。

通常，如何为 LSTM 模型定义输入层存在混淆。

关于如何将可能是 1D 或 2D 数字矩阵的序列数据转换为 LSTM 输入层所需的 3D 格式也存在混淆。

在本教程中，您将了解如何为 LSTM 模型定义输入层以及如何为 LSTM 模型重新加载已加载的输入数据。

完成本教程后，您将了解：

  • 如何定义 LSTM 输入层。
  • 如何重塑 LSTM 模型的一维序列数据并定义输入层。
  • 如何重塑 LSTM 模型的多个并行系列数据并定义输入层。

让我们开始吧。

How to Reshape Input for Long Short-Term Memory Networks in Keras

如何重塑 Keras 长期短期记忆网络的输入
图片来自 Global Landscapes Forum ，保留一些权利。

教程概述

本教程分为 4 个部分;他们是：

  1. LSTM 输入层
  2. 具有单输入样本的 LSTM 示例
  3. 具有多输入功能的 LSTM 示例
  4. LSTM 输入提示

LSTM 输入层

LSTM 输入层由网络的第一个隐藏层上的“input_shape”参数指定。

这会让初学者感到困惑。

例如，下面是具有一个隐藏的 LSTM 层和一个密集输出层的网络的示例。

model = Sequential()
model.add(LSTM(32))
model.add(Dense(1))

在此示例中，LSTM（）层必须指定输入的形状。

每个 LSTM 层的输入必须是三维的。

此输入的三个维度是：

  • 样品。一个序列是一个样本。批次由一个或多个样品组成。
  • 时间步。一个步骤是样品中的一个观察点。
  • 功能。一个特征是在一个时间步骤的一个观察。

这意味着输入层在拟合模型和做出预测时需要 3D 数据数组，即使数组的特定尺寸包含单个值，例如，一个样本或一个特征。

定义 LSTM 网络的输入层时，网络假定您有一个或多个样本，并要求您指定时间步数和要素数。您可以通过指定“input_shape”参数的元组来完成此操作。

例如，下面的模型定义了一个输入层，该输入层需要 1 个或更多样本，50 个时间步长和 2 个特征。

model = Sequential()
model.add(LSTM(32, input_shape=(50, 2)))
model.add(Dense(1))

现在我们知道了如何定义 LSTM 输入层以及 3D 输入的期望，让我们看看如何为 LSTM 准备数据的一些示例。

单输入样本的 LSTM 示例

考虑具有多个时间步长和一个特征的一个序列的情况。

例如，这可能是 10 个值的序列：

0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0

我们可以将这个数字序列定义为 NumPy 数组。

from numpy import array
data = array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0])

然后我们可以使用 NumPy 数组上的 reshape（） 函数将这个一维数组重新整形为一个三维数组，每个时间步长有 1 个样本，10 个时间步长和 1 个特征。

在数组上调用时， reshape（） 函数接受一个参数，该参数是定义数组新形状的元组。我们不能传递任何数字元组;重塑必须均匀地重新组织数组中的数据。

data = data.reshape((1, 10, 1))

重新成形后，我们可以打印数组的新形状。

print(data.shape)

将所有这些放在一起，下面列出了完整的示例。

from numpy import array
data = array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0])
data = data.reshape((1, 10, 1))
print(data.shape)

运行该示例将打印单个样本的新 3D 形状。

(1, 10, 1)

此数据现在可以用作输入（X）到 LSTM，其 input_shape 为（10,1）。

model = Sequential()
model.add(LSTM(32, input_shape=(10, 1)))
model.add(Dense(1))

具有多输入功能的 LSTM 示例

考虑您有多个并行系列作为模型输入的情况。

例如，这可能是两个并行的 10 个值系列：

series 1: 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0
series 2: 1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1

我们可以将这些数据定义为包含 10 行的 2 列矩阵：

from numpy import array
data = array([
	[0.1, 1.0],
	[0.2, 0.9],
	[0.3, 0.8],
	[0.4, 0.7],
	[0.5, 0.6],
	[0.6, 0.5],
	[0.7, 0.4],
	[0.8, 0.3],
	[0.9, 0.2],
	[1.0, 0.1]])

该数据可以被构造为 1 个样本，具有 10 个时间步长和 2 个特征。

它可以重新整形为 3D 数组，如下所示：

data = data.reshape(1, 10, 2)

Putting all of this together, the complete example is listed below.

from numpy import array
data = array([
	[0.1, 1.0],
	[0.2, 0.9],
	[0.3, 0.8],
	[0.4, 0.7],
	[0.5, 0.6],
	[0.6, 0.5],
	[0.7, 0.4],
	[0.8, 0.3],
	[0.9, 0.2],
	[1.0, 0.1]])
data = data.reshape(1, 10, 2)
print(data.shape)

Running the example prints the new 3D shape of the single sample.

(1, 10, 2)

此数据现在可以用作输入（X）到 LSTM，其 input_shape 为（10,2）。

model = Sequential()
model.add(LSTM(32, input_shape=(10, 2)))
model.add(Dense(1))

更长的工作示例

有关准备数据的完整端到端工作示例，请参阅此帖子：

LSTM 输入提示

本节列出了在准备 LSTM 输入数据时可以帮助您的一些提示。

  • LSTM 输入层必须为 3D。
  • 3 个输入维度的含义是：样本，时间步长和功能。
  • LSTM 输入层由第一个隐藏层上的input_shape参数定义。
  • input_shape参数采用两个值的元组来定义时间步长和特征的数量。
  • 假设样本数为 1 或更多。
  • NumPy 数组上的 reshape（） 功能可用于将您的 1D 或 2D 数据重塑为 3D。
  • reshape（） 函数将元组作为定义新形状的参数。

进一步阅读

如果您要深入了解，本节将提供有关该主题的更多资源。

摘要

在本教程中，您了解了如何为 LSTM 定义输入层以及如何重新整形序列数据以输入 LSTM。

具体来说，你学到了：

  • 如何定义 LSTM 输入层。
  • 如何重塑 LSTM 模型的一维序列数据并定义输入层。
  • 如何重塑 LSTM 模型的多个并行系列数据并定义输入层。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

了解 Keras 中 LSTM 的返回序列和返回状态之间的差异

原文： machinelearningmastery.com/return-sequences-and-return-states-for-lstms-in-keras/

Keras 深度学习库提供了长期短期记忆或 LSTM 循环神经网络的实现。

作为此实现的一部分，Keras API 提供对返回序列和返回状态的访问。在设计复杂的循环神经网络模型（例如编解码器模型）时，这些数据之间的使用和差异可能会令人困惑。

在本教程中，您将发现 Keras 深度学习库中 LSTM 层的返回序列和返回状态的差异和结果。

完成本教程后，您将了解：

  • 返回序列返回每个输入时间步的隐藏状态输出。
  • 该返回状态返回上一个输入时间步的隐藏状态输出和单元状态。
  • 返回序列和返回状态可以同时使用。

让我们开始吧。

Understand the Difference Between Return Sequences and Return States for LSTMs in Keras

理解 Keras 中 LSTM 的返回序列和返回状态之间的差异
照片由 Adrian Curt Dannemann ，保留一些权利。

教程概述

本教程分为 4 个部分;他们是：

  1. 长短期记忆
  2. 返回序列
  3. 返回国家
  4. 返回状态和序列

长短期记忆

长短期记忆（LSTM）是一种由内部门组成的循环神经网络。

与其他循环神经网络不同，网络的内部门允许使用反向传播通过时间或 BPTT 成功训练模型，并避免消失的梯度问题。

在 Keras 深度学习库中，可以使用 LSTM（）类创建 LSTM 层。

创建一层 LSTM 内存单元允许您指定层中的内存单元数。

层内的每个单元或单元具有内部单元状态，通常缩写为“c”，并输出隐藏状态，通常缩写为“h”。

Keras API 允许您访问这些数据，这在开发复杂的循环神经网络架构（如编解码器模型）时非常有用甚至是必需的。

在本教程的其余部分中，我们将查看用于访问这些数据的 API。

返回序列

每个 LSTM 单元将为每个输入输出一个隐藏状态h。

h = LSTM(X)

我们可以在 Keras 中使用一个非常小的模型来演示这一点，该模型具有单个 LSTM 层，该层本身包含单个 LSTM 单元。

在这个例子中，我们将有一个带有 3 个时间步长的输入样本，并在每个时间步骤观察到一个特征：

t1 = 0.1
t2 = 0.2
t3 = 0.3

下面列出了完整的示例。

注意：本文中的所有示例都使用 Keras 功能 API 。

from keras.models import Model
from keras.layers import Input
from keras.layers import LSTM
from numpy import array
# define model
inputs1 = Input(shape=(3, 1))
lstm1 = LSTM(1)(inputs1)
model = Model(inputs=inputs1, outputs=lstm1)
# define input data
data = array([0.1, 0.2, 0.3]).reshape((1,3,1))
# make and show prediction
print(model.predict(data))

运行该示例为输入序列输出单个隐藏状态，具有 3 个时间步长。

鉴于 LSTM 权重和单元状态的随机初始化，您的特定输出值将有所不同。

[[-0.0953151]]

可以访问每个输入时间步的隐藏状态输出。

这可以通过在定义 LSTM 层时将return_sequences属性设置为True来完成，如下所示：

LSTM(1, return_sequences=True)

我们可以使用此更改更新上一个示例。

完整的代码清单如下。

from keras.models import Model
from keras.layers import Input
from keras.layers import LSTM
from numpy import array
# define model
inputs1 = Input(shape=(3, 1))
lstm1 = LSTM(1, return_sequences=True)(inputs1)
model = Model(inputs=inputs1, outputs=lstm1)
# define input data
data = array([0.1, 0.2, 0.3]).reshape((1,3,1))
# make and show prediction
print(model.predict(data))

运行该示例将返回一个 3 个值的序列，一个隐藏状态输出，用于层中单个 LSTM 单元的每个输入时间步长。

[[[-0.02243521]
  [-0.06210149]
  [-0.11457888]]]

栈式 LSTM 层时必须设置 return_sequences = True ，以便第二个 LSTM 层具有三维序列输入。有关更多详细信息，请参阅帖子：

在使用包含在 TimeDistributed 层中的Dense输出层预测输出序列时，您可能还需要访问隐藏状态输出序列。有关详细信息，请参阅此帖子：

返回国家

LSTM 单元或单元层的输出称为隐藏状态。

这很令人困惑，因为每个 LSTM 单元都保留一个不输出的内部状态，称为单元状态，或c。

通常，我们不需要访问单元状态，除非我们正在开发复杂模型，其中后续层可能需要使用另一层的最终单元状态初始化其单元状态，例如在编解码器模型中。

Keras 为 LSTM 层提供了 return_state 参数，该参数将提供对隐藏状态输出（state_h）和单元状态（state_c）的访问。例如：

lstm1, state_h, state_c = LSTM(1, return_state=True)

这可能看起来很混乱，因为 lstm1 和state_h都指向相同的隐藏状态输出。这两个张量分离的原因将在下一节中明确。

我们可以使用下面列出的工作示例演示对 LSTM 层中单元格的隐藏和单元格状态的访问。

from keras.models import Model
from keras.layers import Input
from keras.layers import LSTM
from numpy import array
# define model
inputs1 = Input(shape=(3, 1))
lstm1, state_h, state_c = LSTM(1, return_state=True)(inputs1)
model = Model(inputs=inputs1, outputs=[lstm1, state_h, state_c])
# define input data
data = array([0.1, 0.2, 0.3]).reshape((1,3,1))
# make and show prediction
print(model.predict(data))

运行该示例返回 3 个数组：

  1. 最后一个步骤的 LSTM 隐藏状态输出。
  2. LSTM 隐藏状态输出为最后一个时间步骤（再次）。
  3. 最后一个步骤的 LSTM 单元状态。
[array([[ 0.10951342]], dtype=float32),
 array([[ 0.10951342]], dtype=float32),
 array([[ 0.24143776]], dtype=float32)]

隐藏状态和单元状态又可以用于初始化具有相同数量单元的另一个 LSTM 层的状态。

返回状态和序列

我们可以同时访问隐藏状态序列和单元状态。

这可以通过将 LSTM 层配置为返回序列和返回状态来完成。

lstm1, state_h, state_c = LSTM(1, return_sequences=True, return_state=True)

The complete example is listed below.

from keras.models import Model
from keras.layers import Input
from keras.layers import LSTM
from numpy import array
# define model
inputs1 = Input(shape=(3, 1))
lstm1, state_h, state_c = LSTM(1, return_sequences=True, return_state=True)(inputs1)
model = Model(inputs=inputs1, outputs=[lstm1, state_h, state_c])
# define input data
data = array([0.1, 0.2, 0.3]).reshape((1,3,1))
# make and show prediction
print(model.predict(data))

运行该示例，我们现在可以看到为什么 LSTM 输出张量和隐藏状态输出张量是可分离地声明的。

该层返回每个输入时间步的隐藏状态，然后分别返回上一个时间步的隐藏状态输出和最后一个输入时间步的单元状态。

这可以通过查看返回序列中的最后一个值（第一个数组）与隐藏状态（第二个数组）中的值匹配来确认。

[array([[[-0.02145359],
        [-0.0540871 ],
        [-0.09228823]]], dtype=float32),
 array([[-0.09228823]], dtype=float32),
 array([[-0.19803026]], dtype=float32)]

进一步阅读

如果您希望深入了解，本节将提供有关该主题的更多资源。

摘要

在本教程中，您发现了 Keras 深度学习库中 LSTM 层的返回序列和返回状态的差异和结果。

具体来说，你学到了：

  • 返回序列返回每个输入时间步的隐藏状态输出。
  • 该返回状态返回上一个输入时间步的隐藏状态输出和单元状态。
  • 返回序列和返回状态可以同时使用。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

RNN 展开的温和介绍

原文： machinelearningmastery.com/rnn-unrolling/

循环神经网络是一种神经网络，其中来自先前时间步长的输出作为输入馈送到当前时间步长。

这会创建一个带有周期的网络图或电路图，这使得很难理解信息如何通过网络传输。

在这篇文章中，您将发现展开或展开循环神经网络的概念。

阅读这篇文章后，你会知道：

  • 具有循环连接的循环神经网络的标准概念。
  • 在为每个输入时间步骤复制网络时展开正向传递的概念。
  • 在训练期间展开用于更新网络权重的反向传递的概念。

让我们开始吧。

展开循环神经网络

循环神经网络是一种神经网络，其中来自先前时间步长的输出被当作当前时间步长的输入。

我们可以用图片来证明这一点。

下面我们可以看到网络将前一时间步的网络输出作为输入，并使用前一时间步的内部状态作为当前时间步的起点。

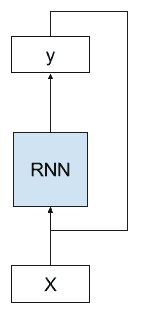
Example of an RNN with a cycle

具有循环的 RNN 的示例

RNN 适合并在许多时间步骤上做出预测。我们可以通过在输入序列上展开或展开 RNN 图来简化模型。

可视化 RNN 的有用方法是考虑通过沿输入序列“展开”网络形成的更新图。

展开远期通行证

考虑我们有多个输入时间步长（X（t），X（t + 1），…），内部状态的多个时间步长（u（t），u（t + 1），…）的情况，以及输出的多个时间步长（y（t），y（t + 1），…）。

我们可以将上述网络示意图展开成没有任何周期的图形。

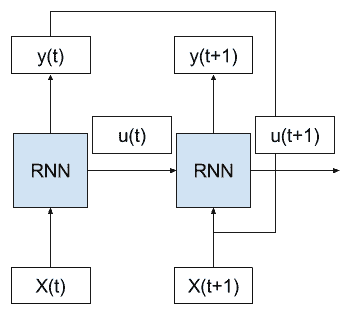
Example of Unrolled RNN on the forward pass

正向通过时展开的 RNN 示例

我们可以看到循环被移除，并且来自前一时间步的输出（y（t））和内部状态（u（t））作为输入传递到网络以处理下一个时间步。

这种概念化的关键是网络（RNN）在展开的时间步骤之间不会改变。具体而言，每个时间步长使用相同的权重，只有输出和内部状态不同。

这样，就好像输入序列中的每个时间步都复制了整个网络（拓扑和权重）。

此外，网络的每个副本可以被认为是相同前馈神经网络的附加层。

Example of Unrolled RNN with each copy of the network as a layer

展开的 RNN 示例，每个网络副本作为一个层

一旦及时展开，RNN 可被视为非常深的前馈网络，其中所有层共享相同的权重。

这是一个有用的概念工具和可视化，有助于了解正向传递过程中网络中发生的情况。它可能也可能不是深度学习库实现网络的方式。

展开后退通行证

网络展开的想法在向后传递实现循环神经网络的方式中起着更大的作用。

正如[反向传播到时间]的标准，网络随着时间的推移展开，因此到达层的连接被视为来自前一个时间步。

  • 具有双向 LSTM 和其他神经网络架构的逐帧音素分类，2005

重要的是，给定时间步长的误差反向传播取决于先前时间步骤的网络激活。

通过这种方式，后向传递需要展开网络的概念化。

将错误传播回序列的第一个输入时间步骤，以便可以计算误差梯度并且可以更新网络的权重。

与标准反向传播一样，[反向传播时间]包括重复应用链规则。细微之处在于，对于循环网络，损失函数不仅取决于隐藏层的激活，还取决于其对输出层的影响，还取决于其在下一个时间步长对隐藏层的影响。

展开循环网络图也引入了其他问题。每个时间步都需要一个新的网络副本，这反过来占用内存，特别是对于具有数千或数百万权重的大型网络。随着时间步数攀升到数百个，大型循环网络的内存需求可能会迅速增加。

…需要按输入序列的长度展开 RNN。通过展开 RNN N 次，网络内的每个神经元的激活被复制 N 次，这消耗了大量的存储器，尤其是当序列非常长时。这阻碍了在线学习或改编的小型实现。此外，这种“完全展开”使得多个序列的并行训练在共享存储器模型（例如图形处理单元（GPU））上效率低下

进一步阅读

如果您要深入了解，本节将提供有关该主题的更多资源。

文件

用品

摘要

在本教程中，您发现了展开循环神经网络的可视化和概念工具。

具体来说，你学到了：

  • 具有循环连接的循环神经网络的标准概念。
  • 在为每个输入时间步骤复制网络时展开正向传递的概念。
  • 在训练期间展开用于更新网络权重的反向传递的概念。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

5 个使用 LSTM 循环神经网络的简单序列预测问题的示例

原文： machinelearningmastery.com/sequence-prediction-problems-learning-lstm-recurrent-neural-networks/

序列预测不同于传统的分类和回归问题。

它要求您考虑观察的顺序，并使用具有记忆的长短期记忆（LSTM）循环神经网络等模型，并且可以学习观察之间的任何时间依赖性。

应用 LSTM 来学习如何在序列预测问题上使用它们是至关重要的，为此，您需要一套明确定义的问题，使您能够专注于不同的问题类型和框架。至关重要的是，您可以建立您对序列预测问题如何不同的直觉，以及如何使用像 LSTM 这样复杂的模型来解决它们。

在本教程中，您将发现一套 5 个狭义定义和可扩展的序列预测问题，您可以使用这些问题来应用和了解有关 LSTM 循环神经网络的更多信息。

完成本教程后，您将了解：

  • 简单的记忆任务，用于测试 LSTM 的学习记忆能力。
  • 简单的打印任务，用于测试 LSTM 的学习时间依赖表现力。
  • 用于测试 LSTM 解释能力的简单算术任务。

让我们开始吧。

5 Examples of Simple Sequence Prediction Problems for Learning LSTM Recurrent Neural Networks

5 用于学习 LSTM 循环神经网络的简单序列预测问题示例
照片由 Geraint Otis Warlow ，保留一些权利。

教程概述

本教程分为 5 个部分;他们是：

  1. 序列学习问题
  2. 价值记忆
  3. 打印随机整数
  4. 打印随机子序列
  5. 序列分类

问题的属性

序列问题的设计考虑了一些属性：

  • 缩小。集中于序列预测的一个方面，例如记忆或函数近似。
  • 可扩展。在选择的狭隘焦点上或多或少地变得困难。
  • 重新定型。提出每个问题的两个或更多个框架以支持不同算法学习能力的探索。

我试图提供狭隘的焦点，问题困难和所需的网络架构。

如果您有进一步扩展的想法或类似的精心设计的问题，请在下面的评论中告诉我。

1.序列学习问题

在该问题中，生成 0.0 和 1.0 之间的连续实数值序列。给定过去值的一个或多个时间步长，模型必须预测序列中的下一个项目。

我们可以直接生成这个序列，如下所示：

from numpy import array

# generate a sequence of real values between 0 and 1.
def generate_sequence(length=10):
	return array([i/float(length) for i in range(length)])

print(generate_sequence())

运行此示例将打印生成的序列：

[ 0\. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9]

这可以被视为记忆挑战，如果在前一时间步骤观察，模型必须预测下一个值：

X (samples),	y
0.0,			0.1
0.1,			0.2
0.2,			0.3
...

网络可以记住输入 - 输出对，这很无聊，但会展示网络的功能近似能力。

该问题可以被构造为随机选择的连续子序列作为输入时间步骤和序列中的下一个值作为输出。

X (timesteps),		y
0.4, 0.5, 0.6,		0.7
0.0, 0.2, 0.3,		0.4
0.3, 0.4, 0.5,		0.6
...

这将要求网络学习向最后看到的观察添加固定值或记住所生成问题的所有可能子序列。

该问题的框架将被建模为多对一序列预测问题。

这是测试序列学习的原始特征的简单问题。这个问题可以通过多层感知机网络来解决。

2.价值记忆

问题是要记住序列中的第一个值，并在序列的末尾重复它。

该问题基于用于在 1997 年论文长期短期记忆中证明 LSTM 的“实验 2”。

这可以被视为一步预测问题。

给定序列中的一个值，模型必须预测序列中的下一个值。例如，给定值“0”作为输入，模型必须预测值“1”。

考虑以下两个 5 个整数的序列：

3, 0, 1, 2, 3
4, 0, 1, 2, 4

Python 代码将生成两个任意长度的序列。如果您愿意，可以进一步概括。

def generate_sequence(length=5):
	return [i for i in range(length)]

# sequence 1
seq1 = generate_sequence()
seq1[0] = seq1[-1] = seq1[-2]
print(seq1)
# sequence 2
seq1 = generate_sequence()
seq1[0] = seq1[-1]
print(seq1)

运行该示例生成并打印上述两个序列。

[3, 1, 2, 3, 3]
[4, 1, 2, 3, 4]

可以对整数进行归一化，或者更优选地对单热编码进行归一化。

这些模式引入了皱纹，因为两个序列之间存在冲突的信息，并且模型必须知道每个一步预测的上下文（例如，它当前正在预测的序列），以便正确地预测每个完整序列。

我们可以看到序列的第一个值重复作为序列的最后一个值。这是指示器为模型提供关于它正在处理的序列的上下文。

冲突是从每个序列中的第二个项目到最后一个项目的过渡。在序列 1 中，给出“2”作为输入并且必须预测“3”，而在序列 2 中，给出“2”作为输入并且必须预测“4”。

Sequence 1:

X (samples),	y
...
1,				2
2,				3

Sequence 2:

X (samples),	y
...
1,				2
2,				4

这种皱纹对于防止模型记忆每个序列中的每个单步输入 - 输出值对非常重要，因为序列未知模型可能倾向于这样做。

该成帧将被建模为一对一的序列预测问题。

这是多层感知机和其他非循环神经网络无法学习的问题。必须记住多个样本中序列中的第一个值。

这个问题可以被定义为提供除最后一个值之外的整个序列作为输入时间步长并预测最终值。

X (timesteps),		y
3, 0, 1, 2, 		3
4, 0, 1, 2, 		4

每个时间步仍然一次显示给网络，但网络必须记住第一个时间步的值。不同的是，网络可以通过时间反向传播更好地了解序列之间和长序列之间的差异。

This framing of the problem would be modeled as a many-to-one sequence prediction problem.

同样，多层感知机无法学习这个问题。

3.打印随机整数

在这个问题中，生成随机的整数序列。模型必须记住特定滞后时间的整数，并在序列结束时打印它。

例如，10 个整数的随机序列可以是：

5, 3, 2, 1, 9, 9, 2, 7, 1, 6

该问题可能被设置为在第 5 个时间步骤打印该值，在这种情况下为 9。

下面的代码将生成随机的整数序列。

from random import randint

# generate a sequence of random numbers in [0, 99]
def generate_sequence(length=10):
	return [randint(0, 99) for _ in range(length)]

print(generate_sequence())

运行该示例将生成并打印随机序列，例如：

[47, 69, 76, 9, 71, 87, 8, 16, 32, 81]

可以对整数进行归一化，但更优选地，可以使用单热编码。

该问题的简单框架是打印当前输入值。

yhat(t) = f(X(t))

例如：

X (timesteps),		y
5, 3, 2, 1, 9,		9

这个微不足道的问题可以通过多层感知机轻松解决，并可用于测试线束的校准或诊断。

更具挑战性的问题框架是打印前一时间步的值。

yhat(t) = f(X(t-1))

For example:

X (timesteps),		y
5, 3, 2, 1, 9,		1

这是多层感知机无法解决的问题。

echo 的索引可以进一步推迟，从而对 LSTM 内存产生更多需求。

与上面的“值记忆”问题不同，每个训练时期都会产生一个新的序列。这将要求模型学习泛化打印解，而不是记忆特定序列或随机数序列。

在这两种情况下，问题都将被建模为多对一序列预测问题。

4.打印随机子序列

该问题还涉及生成随机的整数序列。

这个问题要求模型记住并输出输入序列的部分子序列，而不是像前一个问题那样打印单个前一个时间步骤。

最简单的框架将是前一节中的打印问题。相反，我们将专注于序列输出，其中最简单的框架是模型记住并输出整个输入序列。

For example:

X (timesteps),		y
5, 3, 2, 4, 1,		5, 3, 2, 4, 1

这可以被建模为多对一序列预测问题，其中输出序列直接在输入序列中的最后一个值的末尾输出。

这也可以被建模为网络为每个输入时间步长输出一个值，例如，一对一的模式。

更具挑战性的框架是输出输入序列的部分连续子序列。

For example:

X (timesteps),		y
5, 3, 2, 4, 1,		5, 3, 2

这更具挑战性，因为输入数量与输出数量不匹配。这个问题的多对多模型需要更高级的架构，例如编解码器 LSTM。

同样，单热编码将是优选的，尽管该问题可以被建模为标准化整数值。

5.序列分类

该问题被定义为 0 和 1 之间的随机值序列。该序列被作为问题的输入，每个时间步提供一个数字。

二进制标签（0 或 1）与每个输入相关联。输出值均为 0.一旦序列中输入值的累积和超过阈值，则输出值从 0 翻转为 1。

使用序列长度的 1/4 的阈值。

例如，下面是 10 个输入时间步长（X）的序列：

0.63144003 0.29414551 0.91587952 0.95189228 0.32195638 0.60742236 0.83895793 0.18023048 0.84762691 0.29165514

相应的分类输出（y）将是：

0 0 0 1 1 1 1 1 1 1

我们可以用 Python 实现它。

from random import random
from numpy import array
from numpy import cumsum

# create a sequence classification instance
def get_sequence(n_timesteps):
	# create a sequence of random numbers in [0,1]
	X = array([random() for _ in range(n_timesteps)])
	# calculate cut-off value to change class values
	limit = n_timesteps/4.0
	# determine the class outcome for each item in cumulative sequence
	y = array([0 if x < limit else 1 for x in cumsum(X)])
	return X, y

X, y = get_sequence(10)
print(X)
print(y)

运行该示例会生成随机输入序列，并计算二进制值的相应输出序列。

[ 0.31102339  0.66591885  0.7211718   0.78159441  0.50496384  0.56941485
  0.60775583  0.36833139  0.180908    0.80614878]
[0 0 0 0 1 1 1 1 1 1]

这是一个序列分类问题，可以建模为一对一。状态需要解释过去的时间步骤，以正确预测输出序列何时从 0 翻转到 1。

进一步阅读

如果您要深入了解，本节将提供有关该主题的更多资源。

摘要

在本教程中，您发现了一套精心设计的人工序列预测问题，可用于探索 LSTM 循环神经网络的学习和记忆功能。

具体来说，你学到了：

  • 简单的记忆任务，用于测试 LSTM 的学习记忆能力。
  • 简单的打印任务，用于测试 LSTM 的学习时间依赖表现力。
  • 用于测试 LSTM 解释能力的简单算术任务。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

使用序列做出预测

原文： machinelearningmastery.com/sequence-prediction/

序列预测不同于其他类型的监督学习问题。

该序列对训练模型和做出预测时必须保留的观察结果施加顺序。

通常，涉及序列数据的预测问题被称为序列预测问题，尽管存在一组基于输入和输出序列而不同的问题。

在本教程中，您将发现不同类型的序列预测问题。

完成本教程后，您将了解：

  • 4 种类型的序列预测问题。
  • 专家对每种序列预测问题的定义。
  • 每种类型的序列预测问题的真实示例。

让我们开始吧。

Gentle Introduction to Making Predictions with Sequences

使用序列做出预测的温和介绍
照 abstrkt.ch ，保留一些权利。

教程概述

本教程分为 5 个部分;他们是：

  1. 序列
  2. 序列预测
  3. 序列分类
  4. 序列生成
  5. 序列到序列预测

序列

我们经常处理应用机器学习中的集合，例如训练或测试样本集。

集合中的每个样本可以被认为是来自域的观察。

在一组中，观察的顺序并不重要。

序列不同。该序列对观察结果强加了明确的顺序。

订单很重要。在使用序列数据作为模型的输入或输出的预测问题的制定中必须遵守它。

序列预测

序列预测涉及预测给定输入序列的下一个值。

例如：

  • 鉴于：1,2,3,4,5
  • 预测：6

Example of a Sequence Prediction Problem

序列预测问题的示例

序列预测试图基于前面的元素来预测序列的元素

使用一组训练序列训练预测模型。一旦训练，该模型用于执行序列预测。预测包括预测序列的下一项。此任务有许多应用程序，如网页预取，消费者产品推荐，天气预报和股票市场预测。

序列预测通常也可称为“_ 序列学习 _”。

学习顺序数据仍然是模式识别和机器学习中的一项基本任务和挑战。涉及顺序数据的应用可能需要预测新事件，产生新序列，或决策制定，例如序列或子序列的分类。

从技术上讲，我们可以将这篇文章中的所有以下问题都称为一种序列预测问题。这会让初学者感到困惑。

序列预测问题的一些例子包括：

  • 天气预报。鉴于随着时间的推移对天气的一系列观察，预测明天的预期天气。
  • 股市预测。给定安全性随时间的一系列移动，预测安全性的下一个移动。
  • 产品推荐。给定一系列过去购买的客户，预测下一次购买客户。

序列分类

序列分类涉及预测给定输入序列的类标签。

For example:

  • 鉴于：1,2,3,4,5
  • 预测：“好”或“坏”

Example of a Sequence Classification Problem

序列分类问题的示例

序列分类的目的是使用标记的数据集 D 建立分类模型，以便该模型可用于预测看不见的序列的类标签。

输入序列可以包括实数值或离散值。在后一种情况下，这些问题可以称为离散序列分类。

序列分类问题的一些例子包括：

  • DNA 序列分类。给定 ACGT 值的 DNA 序列，预测序列是否编码编码区或非编码区。
  • 异常检测。给定一系列观察结果，预测序列是否异常。
  • 情感分析。给定一系列文本，如评论或推文，预测文本的情感是正面还是负面。

序列生成

序列生成涉及生成新的输出序列，其具有与语料库中的其他序列相同的一般特征。

For example:

  • 鉴于：[1,3,5]，[7,9,11]
  • 预测：[3,5,7]

[循环神经网络]可以通过一次一步地处理实际数据序列并预测接下来会发生什么来训练序列生成。假设预测是概率性的，则可以通过从网络的输出分布迭代采样从训练的网络生成新的序列，然后在下一步骤中将样本作为输入馈入。换句话说，通过让网络将其发明看作是真实的，就像一个人在做梦

序列生成问题的一些示例包括：

  • 文字生成。给定一组文本，例如莎士比亚的作品，生成新的句子或段落的文字，如莎士比亚。
  • 手写预测。给定手写示例语料库，为在语料库中具有手写属性的新短语生成手写。
  • 音乐生成。给定一组音乐示例，生成具有语料库属性的新音乐作品。

序列生成还可以指给定单个观察作为输入的序列的生成。

一个例子是图像的自动文本描述。

  • 图像标题生成。给定图像作为输入，生成描述图像的单词序列。

Example of a Sequence Generation Problem

序列生成问题的示例

能够使用正确形成的英语句子自动描述图像的内容是一项非常具有挑战性的任务，但它可以产生很大的影响，例如通过帮助视障人士更好地理解网络上的图像内容。 […]实际上，描述不仅必须捕获图像中包含的对象，还必须表达这些对象如何相互关联以及它们的属性和它们所涉及的活动。此外，上述语义知识具有用英语等自然语言表达，这意味着除了视觉理解之外还需要语言模型。

序列到序列预测

序列到序列预测涉及在给定输入序列的情况下预测输出序列。

For example:

  • 鉴于：1,2,3,4,5
  • 预测：6,7,8,9,10

Example of a Sequence-to-Sequence Prediction Problem.png

序列到序列预测问题的示例

尽管它们具有灵活性和功能，但[深度神经网络]只能应用于输入和目标可以用固定维数向量进行合理编码的问题。这是一个重要的限制，因为许多重要问题最好用长度未知的序列表达。例如，语音识别和机器翻译是顺序问题。同样，问答也可以被视为将表示问题的单词序列映射到表示答案的单词序列。

这是序列预测的微妙但具有挑战性的扩展，其中不是预测序列中的单个下一个值，而是预测新序列可以具有或不具有与输入序列相同的长度或者与输入序列具有相同的时间。

这种类型的问题最近在自动文本翻译领域（例如，将英语翻译成法语）进行了大量研究，并且可以通过缩写 seq2seq 来引用。

seq2seq 学习的核心是使用循环神经网络将可变长度输入序列映射到可变长度输出序列。虽然相对较新，但 seq2seq 方法不仅在其原始应用 - 机器翻译方面取得了最先进的成果。

如果输入和输出序列是时间序列，则该问题可以称为多步时间序列预测。

  • 多步时间序列预测。给定时间序列的观察，预测一系列未来时间步骤的观察结果。
  • 文字摘要。给定文本文档，预测描述源文档的显着部分的较短文本序列。
  • 程序执行。给定文本描述程序或数学方程，预测描述正确输出的字符序列。

进一步阅读

如果您要深入了解，本节将提供有关该主题的更多资源。

摘要

在本教程中，您发现了不同类型的序列预测问题。

具体来说，你学到了：

  • 4 种类型的序列预测问题。
  • 专家对每种序列预测问题的定义。
  • 每种类型的序列预测问题的真实示例。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

栈式长短期记忆网络

原文： machinelearningmastery.com/stacked-long-short-term-memory-networks/

使用 Python 中的示例代码轻松介绍 Stacked LSTM

。

原始 LSTM 模型由单个隐藏的 LSTM 层和后面的标准前馈输出层组成。

Stacked LSTM 是此模型的扩展，具有多个隐藏的 LSTM 层，其中每个层包含多个存储器单元。

在这篇文章中，您将发现 Stacked LSTM 模型架构。

完成本教程后，您将了解：

  • 深度神经网络架构的好处。
  • Stacked LSTM 循环神经网络架构。
  • 如何使用 Keras 在 Python 中实现栈式 LSTM。

让我们开始吧。

Gentle Introduction to Stacked Long Short-Term Memory Networks

堆叠长短期记忆网络
的照片由 Joost Markerink 拍摄，保留一些权利。

概观

这篇文章分为 3 个部分，它们是：

  1. 为什么要增加深度？
  2. 栈式 LSTM 架构
  3. 在 Keras 中实现栈式 LSTM

为什么要增加深度？

栈式 LSTM 隐藏层使得模型更深入，更准确地将描述作为深度学习技术获得。

神经网络的深度通常归因于该方法在广泛的挑战性预测问题上的成功。

[深度神经网络的成功]通常归因于由于多个层而引入的层次结构。每个层处理我们希望解决的任务的某些部分，并将其传递给下一个。从这个意义上讲，DNN 可以看作是一个处理流水线，其中每个层在将任务传递给下一个任务之前解决了部分任务，直到最后一层提供输出。

可以将其他隐藏层添加到多层感知机神经网络中以使其更深。附加隐藏层被理解为重新组合来自先前层的学习表示并在高抽象级别创建新表示。例如，从线到形状到对象。

足够大的单个隐藏层多层感知机可用于近似大多数功能。增加网络的深度提供了另一种解决方案，需要更少的神经元和更快的训练。最终，添加深度是一种代表性优化。

深度学习是围绕一个假设建立的，即深层次分层模型在表示某些函数时可以指数级更高效，而不是浅层函数。

栈式 LSTM 架构

LSTM 可以利用相同的好处。

鉴于 LSTM 对序列数据进行操作，这意味着层的添加增加了输入观察随时间的抽象级别。实际上，随着时间的推移进行分块观察或在不同时间尺度上表示问题。

…通过将多个重复隐藏状态堆叠在一起来构建深 RNN。该方法可能允许每个级别的隐藏状态在不同的时间尺度上操作

Graves 等人介绍了堆叠的 LSTM 或深 LSTM。在将 LSTM 应用于语音识别方面，打破了具有挑战性的标准问题的基准。

RNN 本身就具有深度，因为它们的隐藏状态是所有先前隐藏状态的函数。启发本文的问题是 RNN 是否也能从太空深度中获益;这就是将多个重复隐藏层堆叠在一起，就像在传统的深层网络中堆叠前馈层一样。

在同样的工作中，他们发现网络的深度比给定层中的存储器单元的数量更重要。

栈式 LSTM 现在是用于挑战序列预测问题的稳定技术。栈式 LSTM 架构可以定义为由多个 LSTM 层组成的 LSTM 模型。上面的 LSTM 层提供序列输出而不是单个值输出到下面的 LSTM 层。具体地说，每个输入时间步长一个输出，而不是所有输入时间步长的一个输出时间步长。

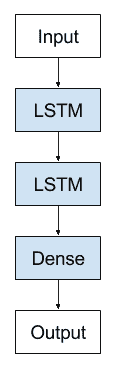
Stacked Long Short-Term Memory Archiecture

堆叠长短期内存架构

在 Keras 中实现栈式 LSTM

我们可以在 Keras Python 深度学习库中轻松创建 Stacked LSTM 模型

每个 LSTM 存储器单元都需要 3D 输入。当 LSTM 处理一个输入时间步长序列时，每个存储器单元将输出整个序列的单个值作为 2D 数组。

我们可以使用具有单个隐藏 LSTM 层的模型来演示以下内容，该 LSTM 层也是输出层。

# Example of one output for whole sequence
from keras.models import Sequential
from keras.layers import LSTM
from numpy import array
# define model where LSTM is also output layer
model = Sequential()
model.add(LSTM(1, input_shape=(3,1)))
model.compile(optimizer='adam', loss='mse')
# input time steps
data = array([0.1, 0.2, 0.3]).reshape((1,3,1))
# make and show prediction
print(model.predict(data))

输入序列有 3 个值。运行该示例将输入序列的单个值输出为 2D 数组。

[[ 0.00031043]]

要栈式 LSTM 层，我们需要更改先前 LSTM 层的配置，以输出 3D 数组作为后续层的输入。

我们可以通过将层上的 return_sequences 参数设置为 True（默认为 False）来完成此操作。这将为每个输入时间步返回一个输出并提供 3D 数组。
以下是与 return_sequences = True 相同的例子。

# Example of one output for each input time step
from keras.models import Sequential
from keras.layers import LSTM
from numpy import array
# define model where LSTM is also output layer
model = Sequential()
model.add(LSTM(1, return_sequences=True, input_shape=(3,1)))
model.compile(optimizer='adam', loss='mse')
# input time steps
data = array([0.1, 0.2, 0.3]).reshape((1,3,1))
# make and show prediction
print(model.predict(data))

运行该示例为输入序列中的每个时间步输出单个值。

[[[-0.02115841]
[-0.05322712]
[-0.08976141]]]

下面是定义两个隐藏层 Stacked LSTM 的示例：

model = Sequential()
model.add(LSTM(..., return_sequences=True, input_shape=(...)))
model.add(LSTM(...))
model.add(Dense(...))

只要先前的 LSTM 层提供 3D 输出作为后续层的输入，我们就可以继续添加隐藏的 LSTM 层。例如，下面是一个有 4 个隐藏层的 Stacked LSTM。

model = Sequential()
model.add(LSTM(..., return_sequences=True, input_shape=(...)))
model.add(LSTM(..., return_sequences=True))
model.add(LSTM(..., return_sequences=True))
model.add(LSTM(...))
model.add(Dense(...))

进一步阅读

如果您要深入了解，本节将提供有关该主题的更多资源。

摘要

在这篇文章中，您发现了 Stacked Long Short-Term Memory 网络架构。

具体来说，你学到了：

  • 深度神经网络架构的好处。
  • Stacked LSTM 循环神经网络架构。
  • 如何使用 Keras 在 Python 中实现栈式 LSTM。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

什么是循环神经网络的教师强制？

原文： machinelearningmastery.com/teacher-forcing-for-recurrent-neural-networks/

教师强制是一种快速有效地训练循环神经网络模型的方法，该模型使用来自先前时间步长的输出作为输入。

它是一种网络训练方法，对于开发用于机器翻译，文本摘要和图像字幕的深度学习语言模型以及许多其他应用程序至关重要。

在这篇文章中，您将发现教师强迫作为训练复现神经网络的方法。

阅读这篇文章后，你会知道：

  • 训练循环神经网络的问题是使用先前时间步长的输出作为输入。
  • 在训练这些类型的循环网络时，教师强制解决缓慢收敛和不稳定的方法。
  • 教师强迫的扩展允许训练有素的模型更好地处理这种类型网络的开环应用。

让我们开始吧。

What is Teacher Forcing for Recurrent Neural Networks?

什么是教师强制循环神经网络？
Nathan Russell 的照片，保留一些权利。

在序列预测中使用输出作为输入

存在序列预测模型，其使用来自上一时间步骤 y（t-1）的输出作为当前时间步骤 X（t）处的模型的输入。

这种类型的模型在语言模型中很常见，它一次输出一个单词并使用输出单词作为输入来生成序列中的下一个单词。

例如，这种类型的语言模型用于编解码器循环神经网络架构中，用于序列到序列生成问题，例如：

  • 机器翻译
  • 标题生成
  • 文本摘要

在训练模型之后，可以使用“序列开始”标记来启动过程，并且输出序列中生成的单词在后续时间步骤中用作输入，可能与其他输入一样，如图像或源文本。

在训练模型时可以使用相同的递归输出输入过程，但它可能导致以下问题：

  • 收敛缓慢。
  • 模型不稳定。
  • 技能差。

在训练这些类型的模型时，教师强制是一种提高模型技能和稳定性的方法。

什么是教师强迫？

教师强制是一种训练循环神经网络的策略，它使用先前时间步长的模型输出作为输入。

从输出返回到模型中的经常连接的模型可以通过教师强制进行训练。

最初描述和开发该方法作为反向传播的替代技术用于训练复发神经网络。

在动态监督学习任务中经常使用的一种有趣的技术是，在存在这样的值时，在随后的网络行为计算中用教师信号 d（t）替换单元的实际输出 y（t）。我们称这种技术教师为强迫。

教师强制通过在当前时间步骤 y（t）使用来自训练数据集的实际或预期输出作为下一时间步骤 X（t + 1）中的输入而不是由网络生成的输出来工作。

教师强迫是一种程序，其中在训练期间，模型在时间 t + 1 接收地面实况输出 y（t）作为输入。

— Page 372, Deep Learning, 2016.

工作示例

让我们通过一个简短的例子让教师强制具体化。

给定以下输入序列：

Mary had a little lamb whose fleece was white as snow

想象一下，我们想要训练一个模型，在给定前一个单词序列的情况下生成序列中的下一个单词。

首先，我们必须添加一个标记来表示序列的开始，另一个标记来表示序列的结束。我们将分别使用“ [START] ”和“ [END] ”。

[START] Mary had a little lamb whose fleece was white as snow [END]

接下来，我们输入模型“ [START] ”并让模型生成下一个单词。

想象一下，该模型生成单词“a”，但当然，我们期望“Mary”。

X,						yhat
[START],				a

朴素地，我们可以输入“a”作为输入的一部分，以生成序列中的后续单词。

X,						yhat
[START], a,				?

您可以看到模型偏离轨道，并且会因为它生成的每个后续单词而受到惩罚。这使学习速度变慢，模型不稳定。

相反，我们可以使用教师强制。

在第一个例子中，当模型生成“a”作为输出时，我们可以在计算错误后丢弃此输出并输入“Mary”作为后续时间步的输入的一部分。

X,						yhat
[START], Mary,			?

然后，我们可以为每个输入 - 输出字对重复此过程。

X,						yhat
[START], 				?
[START], Mary,			?
[START], Mary, had,		?
[START], Mary, had, a,	?
...

该模型将快速学习正确的序列，或更正序列的统计属性。

教师强迫的延伸

教师强制是一种快速有效的方法，用于训练循环神经网络，该网络使用先前时间步长的输出作为模型的输入。

但是，当生成的序列与训练期间模型所看到的不同时，该方法还可能导致在实践中使用时可能脆弱或受限的模型。

这在这种类型的模型的大多数应用中是常见的，因为输出本质上是概率性的。这种类型的模型应用通常称为开环。

不幸的是，该过程可能导致在调节环境中作为小预测误差化合物的生成问题。这会导致预测表现较差，因为 RNN 的调节环境（先前生成的样本的序列）与训练期间看到的序列不同。

有许多方法可以解决这个限制，例如：

搜索候选输出序列

通常用于预测离散值输出（例如单词）的模型的一种方法是对每个单词的预测概率执行搜索以生成多个可能的候选输出序列。

此方法用于机器翻译等问题，以优化翻译的输出序列。

该事后操作的常见搜索过程是集束搜索。

通过使用保持若干生成的目标序列的集束搜索启发式可以减轻这种差异

课程学习

集束搜索方法仅适用于具有离散输出值的预测问题，不能用于实值输出。

强迫学习的一种变化是在训练期间引入先前时间步骤产生的输出，以鼓励模型学习如何纠正自己的错误。

我们建议改变训练过程，以逐步强迫模型处理自己的错误，就像在推理过程中一样。

— Scheduled Sampling for Sequence Prediction with Recurrent Neural Networks, 2015.

该方法称为课程学习，涉及随机选择使用地面实况输出或前一时间步的生成输出作为当前时间步的输入。

课程在所谓的预定采样中随时间而变化，其中程序从强制学习开始，并且慢慢降低在训练时期内强制输入的概率。

还有其他教师强制的扩展和变体，如果您有兴趣，我鼓励您探索它们。

进一步阅读

如果您要深入了解，本节将提供有关该主题的更多资源。

文件

图书

  • 第 10.2.1 节，教师强制和输出复发网络，深度学习，2016 年。

摘要

在这篇文章中，您发现教师强制作为训练循环神经网络的方法，该神经网络使用前一时间步的输出作为输入。

具体来说，你学到了：

  • 训练循环神经网络的问题是使用先前时间步长的输出作为输入。
  • 在训练这些类型的循环网络时，教师强制解决缓慢收敛和不稳定的方法。
  • 教师强迫的扩展允许训练有素的模型更好地处理这种类型网络的开环应用。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

如何在 Python 中对长短期记忆网络使用TimeDistributed层

原文： machinelearningmastery.com/timedistributed-layer-for-long-short-term-memory-networks-in-python/

长期短期网络或 LSTM 是一种流行且功能强大的循环神经网络或 RNN。

它们可能很难配置并应用于任意序列预测问题，即使使用定义良好且“易于使用”的接口，如 Python 中的 Keras 深度学习库中提供的那些接口也是如此。

在 Keras 中遇到这种困难的一个原因是使用了 TimeDistributed 包装层，并且需要一些 LSTM 层来返回序列而不是单个值。

在本教程中，您将发现为序列预测配置 LSTM 网络的不同方法，TimeDistributed 层所扮演的角色以及如何使用它。

完成本教程后，您将了解：

  • 如何设计一对一的 LSTM 用于序列预测。
  • 如何在没有 TimeDistributed Layer 的情况下设计用于序列预测的多对一 LSTM。
  • 如何使用 TimeDistributed Layer 设计多对多 LSTM 以进行序列预测。

让我们开始吧。

How to Use the TimeDistributed Layer for Long Short-Term Memory Networks in Python

如何在 Python 中使用 TimeDistributed Layer for Long Short-Term Memory Networks
jans canon 的照片，保留一些权利。

教程概述

本教程分为 5 个部分;他们是：

  1. TimeDistributed Layer
  2. 序列学习问题
  3. 用于序列预测的一对一 LSTM
  4. 用于序列预测的多对一 LSTM（没有 TimeDistributed）
  5. 用于序列预测的多对多 LSTM（具有 TimeDistributed）

环境

本教程假定安装了 SciPy，NumPy 和 Pandas 的 Python 2 或 Python 3 开发环境。

本教程还假设 scikit-learn 和 Keras v2.0 +与 Theano 或 TensorFlow 后端一起安装。

有关设置 Python 环境的帮助，请参阅帖子：

TimeDistributed Layer

LSTM 功能强大，但难以使用且难以配置，尤其适合初学者。

另一个复杂因素是 TimeDistributed Layer（以及之前的TimeDistributedDense层），它被隐式描述为层包装器：

这个包装器允许我们将一个层应用于输入的每个时间片。

你应该如何以及何时使用 LSTM 的这个包装器？

当您在 Keras GitHub 问题和 StackOverflow 上搜索有关包装层的讨论时，这种混淆更加复杂。

例如，在问题“何时以及如何使用 TimeDistributedDense ”中，“fchollet（Keras’作者）解释说：

TimeDistributedDense 对 3D 张量的每个时间步应用相同的 Dense（完全连接）操作。

如果您已经了解 TimeDistributed 层的用途以及何时使用它，那么这是完全合理的，但对初学者来说根本没有帮助。

本教程旨在消除使用带有 LSTM 的 TimeDistributed 包装器的混乱，以及可以检查，运行和使用的工作示例，以帮助您进行具体的理解。

序列学习问题

我们将使用一个简单的序列学习问题来演示 TimeDistributed 层。

在这个问题中，序列[0.0,0.2,0.4,0.6,0.8]将一次作为输入一个项目给出，并且必须依次作为输出返回，一次一个项目。

可以把它想象成一个简单的打印程序。我们给出 0.0 作为输入，我们期望看到 0.0 作为输出，对序列中的每个项重复。

我们可以直接生成这个序列如下：

from numpy import array
length = 5
seq = array([i/float(length) for i in range(length)])
print(seq)

运行此示例将打印生成的序列：

[ 0\.   0.2  0.4  0.6  0.8]

该示例是可配置的，如果您愿意，您可以稍后自己玩更长/更短的序列。请在评论中告诉我您的结果。

用于序列预测的一对一 LSTM

在我们深入研究之前，重要的是要表明这种序列学习问题可以分段学习。

也就是说，我们可以将问题重新构造为序列中每个项目的输入 - 输出对的数据集。给定 0，网络应输出 0，给定 0.2，网络必须输出 0.2，依此类推。

这是问题的最简单的公式，并且要求将序列分成输入 - 输出对，并且序列一次一步地预测并聚集在网络外部。

输入输出对如下：

X, 	y
0.0,	0.0
0.2,	0.2
0.4,	0.4
0.6,	0.6
0.8,	0.8

LSTM 的输入必须是三维的。我们可以将 2D 序列重塑为具有 5 个样本，1 个时间步长和 1 个特征的 3D 序列。我们将输出定义为具有 1 个特征的 5 个样本。

X = seq.reshape(5, 1, 1)
y = seq.reshape(5, 1)

我们将网络模型定义为具有 1 个输入和 1 个时间步长。第一个隐藏层将是一个有 5 个单位的 LSTM。输出层是一个带有 1 个输出的全连接层。

该模型将适用于有效的 ADAM 优化算法和均方误差损失函数。

批量大小设置为时期中的样本数量，以避免必须使 LSTM 有状态并手动管理状态重置，尽管这可以很容易地完成，以便在每个样本显示到网络后更新权重。

完整的代码清单如下：

from numpy import array
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
# prepare sequence
length = 5
seq = array([i/float(length) for i in range(length)])
X = seq.reshape(len(seq), 1, 1)
y = seq.reshape(len(seq), 1)
# define LSTM configuration
n_neurons = length
n_batch = length
n_epoch = 1000
# create LSTM
model = Sequential()
model.add(LSTM(n_neurons, input_shape=(1, 1)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
print(model.summary())
# train LSTM
model.fit(X, y, epochs=n_epoch, batch_size=n_batch, verbose=2)
# evaluate
result = model.predict(X, batch_size=n_batch, verbose=0)
for value in result:
	print('%.1f' % value)

首先运行该示例将打印已配置网络的结构。

我们可以看到 LSTM 层有 140 个参数。这是根据输入数量（1）和输出数量（隐藏层中 5 个单位为 5）计算的，如下所示：

n = 4 * ((inputs + 1) * outputs + outputs²)
n = 4 * ((1 + 1) * 5 + 5²)
n = 4 * 35
n = 140

我们还可以看到，完全连接的层只有 6 个参数用于输入数量（5 个用于前一层的 5 个输入），输出数量（1 个用于层中的 1 个神经元）和偏差。

n = inputs * outputs + outputs
n = 5 * 1 + 1
n = 6

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
lstm_1 (LSTM)                (None, 1, 5)              140
_________________________________________________________________
dense_1 (Dense)              (None, 1, 1)              6
=================================================================
Total params: 146.0
Trainable params: 146
Non-trainable params: 0.0
_________________________________________________________________

网络正确地学习预测问题。

0.0
0.2
0.4
0.6
0.8

用于序列预测的多对一 LSTM（没有 TimeDistributed）

在本节中，我们开发了一个 LSTM 来一次输出序列，尽管没有 TimeDistributed 包装层。

LSTM 的输入必须是三维的。我们可以将 2D 序列重塑为具有 1 个样本，5 个时间步长和 1 个特征的 3D 序列。我们将输出定义为具有 5 个特征的 1 个样本。

X = seq.reshape(1, 5, 1)
y = seq.reshape(1, 5)

您可以立即看到，必须稍微调整问题定义，以便在没有 TimeDistributed 包装器的情况下支持网络进行序列预测。具体来说，输出一个向量而不是一次一步地构建输出序列。差异可能听起来很微妙，但了解 TimeDistributed 包装器的作用非常重要。

我们将模型定义为具有 5 个时间步长的一个输入。第一个隐藏层将是一个有 5 个单位的 LSTM。输出层是一个完全连接的层，有 5 个神经元。

# create LSTM
model = Sequential()
model.add(LSTM(5, input_shape=(5, 1)))
model.add(Dense(length))
model.compile(loss='mean_squared_error', optimizer='adam')
print(model.summary())

接下来，我们将模型仅适用于训练数据集中的单个样本的 500 个迭代和批量大小为 1。

# train LSTM
model.fit(X, y, epochs=500, batch_size=1, verbose=2)

综合这些，下面提供了完整的代码清单。

from numpy import array
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
# prepare sequence
length = 5
seq = array([i/float(length) for i in range(length)])
X = seq.reshape(1, length, 1)
y = seq.reshape(1, length)
# define LSTM configuration
n_neurons = length
n_batch = 1
n_epoch = 500
# create LSTM
model = Sequential()
model.add(LSTM(n_neurons, input_shape=(length, 1)))
model.add(Dense(length))
model.compile(loss='mean_squared_error', optimizer='adam')
print(model.summary())
# train LSTM
model.fit(X, y, epochs=n_epoch, batch_size=n_batch, verbose=2)
# evaluate
result = model.predict(X, batch_size=n_batch, verbose=0)
for value in result[0,:]:
	print('%.1f' % value)

首先运行该示例将打印已配置网络的摘要。

我们可以看到 LSTM 层有 140 个参数，如上一节所述。

LSTM 单元已经瘫痪，每个单元都输出一个值，提供 5 个值的向量作为完全连接层的输入。时间维度或序列信息已被丢弃并折叠成 5 个值的向量。

我们可以看到完全连接的输出层有 5 个输入，预计输出 5 个值。我们可以解释如下要学习的 30 个权重：

n = inputs * outputs + outputs
n = 5 * 5 + 5
n = 30

网络摘要报告如下：

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
lstm_1 (LSTM)                (None, 5)                 140
_________________________________________________________________
dense_1 (Dense)              (None, 5)                 30
=================================================================
Total params: 170.0
Trainable params: 170
Non-trainable params: 0.0
_________________________________________________________________

该模型适合，在最终确定和打印预测序列之前打印损失信息。

序列被正确再现，但是作为单个部分而不是逐步通过输入数据。我们可能使用 Dense 层作为第一个隐藏层而不是 LSTM，因为 LSTM 的这种使用并没有充分利用它们完整的序列学习和处理能力。

0.0
0.2
0.4
0.6
0.8

用于序列预测的多对多 LSTM（具有 TimeDistributed）

在本节中，我们将使用 TimeDistributed 层来处理 LSTM 隐藏层的输出。

使用 TimeDistributed 包装层时要记住两个关键点：

  • 输入必须（至少）为 3D 。这通常意味着您需要在 TimeDistributed wrapped Dense 层之前配置最后一个 LSTM 层以返回序列（例如，将“return_sequences”参数设置为“True”）。
  • 输出为 3D 。这意味着如果 TimeDistributed 包裹的 Dense 层是输出层并且您正在预测序列，则需要将 y 数组的大小调整为 3D 向量。

我们可以将输出的形状定义为具有 1 个样本，5 个时间步长和 1 个特征，就像输入序列一样，如下所示：

y = seq.reshape(1, length, 1)

我们可以通过将“return_sequences”参数设置为 true 来定义 LSTM 隐藏层以返回序列而不是单个值。

model.add(LSTM(n_neurons, input_shape=(length, 1), return_sequences=True))

这具有每个 LSTM 单元返回 5 个输出序列的效果，输出数据中的每个时间步长一个输出，而不是如前一示例中的单个输出值。

我们还可以使用输出层上的 TimeDistributed 来包装具有单个输出的完全连接的 Dense 层。

model.add(TimeDistributed(Dense(1)))

输出层中的单个输出值是关键。它强调我们打算从输入中的每个时间步的序列输出一个时间步。碰巧我们将一次处理输入序列的 5 个时间步。

TimeDistributed 通过一次一个步骤将相同的 Dense 层（相同的权重）应用于 LSTM 输出来实现此技巧。这样，输出层只需要一个连接到每个 LSTM 单元（加上一个偏置）。

因此，需要增加训练时期的数量以考虑较小的网络容量。我将它从 500 加倍到 1000，以匹配第一个一对一的例子。

将它们放在一起，下面提供了完整的代码清单。

from numpy import array
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import TimeDistributed
from keras.layers import LSTM
# prepare sequence
length = 5
seq = array([i/float(length) for i in range(length)])
X = seq.reshape(1, length, 1)
y = seq.reshape(1, length, 1)
# define LSTM configuration
n_neurons = length
n_batch = 1
n_epoch = 1000
# create LSTM
model = Sequential()
model.add(LSTM(n_neurons, input_shape=(length, 1), return_sequences=True))
model.add(TimeDistributed(Dense(1)))
model.compile(loss='mean_squared_error', optimizer='adam')
print(model.summary())
# train LSTM
model.fit(X, y, epochs=n_epoch, batch_size=n_batch, verbose=2)
# evaluate
result = model.predict(X, batch_size=n_batch, verbose=0)
for value in result[0,:,0]:
	print('%.1f' % value)

运行该示例，我们可以看到已配置网络的结构。

我们可以看到，与前面的示例一样，LSTM 隐藏层中有 140 个参数。

完全连接的输出层是一个非常不同的故事。实际上，它完全符合一对一的例子。一个神经元，对于前一层中的每个 LSTM 单元具有一个权重，加上一个用于偏置输入。

这有两个重要的事情：

  • 允许在定义问题时构建和学习问题，即一个输出到一个输出，保持每个时间步的内部过程分开。
  • 通过要求更少的权重来简化网络，使得一次只处理一个时间步长。

将一个更简单的完全连接层应用于从前一层提供的序列中的每个时间步，以构建输出序列。

_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
lstm_1 (LSTM)                (None, 5, 5)              140
_________________________________________________________________
time_distributed_1 (TimeDist (None, 5, 1)              6
=================================================================
Total params: 146.0
Trainable params: 146
Non-trainable params: 0.0
_________________________________________________________________

同样，网络学习序列。

0.0
0.2
0.4
0.6
0.8

我们可以将时间步长问题框架和 TimeDistributed 层视为在第一个示例中实现一对一网络的更紧凑方式。它甚至可能在更大规模上更有效（空间或时间）。

进一步阅读

以下是您可能希望深入研究的 TimeDistributed 层的一些资源和讨论。

摘要

在本教程中，您了解了如何为序列预测开发 LSTM 网络以及 TimeDistributed 层的作用。

具体来说，你学到了：

  • 如何设计一对一的 LSTM 用于序列预测。
  • 如何在没有 TimeDistributed Layer 的情况下设计用于序列预测的多对一 LSTM。
  • 如何使用 TimeDistributed Layer 设计多对多 LSTM 以进行序列预测。

你有任何问题吗？
在下面的评论中提出您的问题，我会尽力回答。

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值