Machine Learning Mastery 集成学习教程（一）

原文：Machine Learning Mastery

协议：CC BY-NC-SA 4.0

如何用 Python 开发 AdaBoost 集成

原文：https://machinelearningmastery.com/adaboost-ensemble-in-python/

最后更新于 2021 年 4 月 27 日

Boosting 是一类集成机器学习算法，它涉及组合来自许多弱学习器的预测。

弱学习器是一个非常简单的模型，尽管在数据集上有一些技巧。在开发出实用算法之前，Boosting 是一个理论概念，AdaBoost(自适应 boosting)算法是实现这一想法的第一个成功方法。

AdaBoost 算法包括使用非常短的(一级)决策树作为弱学习器，它们被顺序添加到集成中。每个随后的模型都试图纠正序列中它之前的模型所做的预测。这是通过对训练数据集进行加权来实现的，以将更多的注意力放在先前模型产生预测误差的训练示例上。

在本教程中，您将发现如何开发用于分类和回归的 AdaBoost 集成。

完成本教程后，您将知道:

• AdaBoost 集成是从顺序添加到模型中的决策树创建的集成
• 如何使用 AdaBoost 集成与 Sklearn 进行分类和回归。
• 如何探索 AdaBoost 模型超参数对模型表现的影响？

用我的新书Python 集成学习算法启动你的项目，包括分步教程和所有示例的 Python 源代码文件。

我们开始吧。

• 2020 年 8 月更新:增加了网格搜索模型超参数示例。

如何开发 Python 中的 AdaBoost 集成
图片由雷在马尼拉拍摄，保留部分权利。

教程概述

本教程分为四个部分；它们是:

1. AdaBoost 集成算法
2. 学习应用编程接口
   1. 用于分类的 AdaBoost
   2. 回归的 AdaBoost
3. AdaBoost 超参数
   1. 探索树的数量
   2. 探索弱势学习器
   3. 探索学习率
   4. 探索替代算法
4. 网格搜索 AdaBoost 超参数

AdaBoost 集成算法

Boosting 指的是一类机器学习集成算法，其中模型按顺序添加，序列中后面的模型修正序列中前面模型做出的预测。

AdaBoost ，简称“自适应 boosting ”，是一种 Boosting 集成机器学习算法，是最早成功的 Boosting 方法之一。

我们称该算法为 AdaBoost，因为与以前的算法不同，它能自适应地调整弱假设的误差

——在线学习的决策理论推广及其在增强中的应用，1996。

AdaBoost 结合了来自短的一级决策树的预测，称为决策树桩，尽管也可以使用其他算法。决策树桩算法被使用，因为 AdaBoost 算法试图使用许多弱模型，并通过添加额外的弱模型来校正它们的预测。

训练算法包括从一棵决策树开始，在训练数据集中找到那些被错误分类的例子，并给这些例子增加更多的权重。另一棵树是在相同的数据上训练的，尽管现在是由错误分类误差加权的。重复这个过程，直到添加了所需数量的树。

如果训练数据点被错误分类，则该训练数据点的权重增加(提升)。使用不再相等的新权重构建第二个分类器。同样，错误分类的训练数据的权重增加，并且重复该过程。

——多级 AdaBoost ，2009 年。

该算法是为分类而开发的，涉及到组合集合中所有决策树做出的预测。类似的方法也被开发用于回归问题，其中通过使用决策树的平均值进行预测。基于模型在训练数据集上的表现，加权每个模型对集成预测的贡献。

……新算法不需要弱假设准确性的先验知识。相反，它适应这些准确率，并生成加权多数假设，其中每个弱假设的权重是其准确率的函数。

——在线学习的决策理论推广及其在增强中的应用，1996。

现在我们已经熟悉了 AdaBoost 算法，让我们看看如何在 Python 中拟合 AdaBoost 模型。

学习应用编程接口

AdaBoost 集成可以从零开始实现，尽管这对初学者来说可能很有挑战性。

有关示例，请参见教程:

• 机器学习的 Boosting 和 AdaBoost】

Sklearn Python 机器学习库为机器学习提供了 AdaBoost 集成的实现。

它有现代版本的图书馆。

首先，通过运行以下脚本来确认您使用的是现代版本的库:

# check Sklearn version
import sklearn
print(sklearn.__version__)

运行脚本将打印您的 Sklearn 版本。

您的版本应该相同或更高。如果没有，您必须升级 Sklearn 库的版本。

0.22.1

AdaBoost 通过【AdaBoost 渐层和【AdaBoost 分类器类提供。

这两个模型以相同的方式运行，并采用相同的参数来影响决策树的创建。

随机性用于模型的构建。这意味着算法每次在相同的数据上运行时，都会产生稍微不同的模型。

当使用具有随机学习算法的机器学习算法时，最好通过在多次运行或重复交叉验证中平均它们的表现来评估它们。当拟合最终模型时，可能需要增加树的数量，直到模型的方差在重复评估中减小，或者拟合多个最终模型并对它们的预测进行平均。

让我们看看如何为分类和回归开发一个 AdaBoost 集成。

用于分类的 AdaBoost

在本节中，我们将研究使用 AdaBoost 解决分类问题。

首先，我们可以使用 make_classification()函数创建一个包含 1000 个示例和 20 个输入特征的合成二进制分类问题。

下面列出了完整的示例。

# test classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
# summarize the dataset
print(X.shape, y.shape)

运行该示例将创建数据集并总结输入和输出组件的形状。

(1000, 20) (1000,)

接下来，我们可以在这个数据集上评估一个 AdaBoost 算法。

我们将使用重复分层 k 折叠交叉验证来评估模型，重复 3 次，折叠 10 次。我们将报告所有重复和折叠的模型准确率的平均值和标准偏差。

# evaluate adaboost algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import AdaBoostClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
# define the model
model = AdaBoostClassifier()
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到带有默认超参数的 AdaBoost 集成在这个测试数据集上实现了大约 80%的分类准确率。

Accuracy: 0.806 (0.041)

我们也可以将 AdaBoost 模型作为最终模型，进行分类预测。

首先，AdaBoost 集成适合所有可用数据，然后可以调用 predict() 函数对新数据进行预测。

下面的示例在我们的二进制类别数据集上演示了这一点。

# make predictions using adaboost for classification
from sklearn.datasets import make_classification
from sklearn.ensemble import AdaBoostClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
# define the model
model = AdaBoostClassifier()
# fit the model on the whole dataset
model.fit(X, y)
# make a single prediction
row = [[-3.47224758,1.95378146,0.04875169,-0.91592588,-3.54022468,1.96405547,-7.72564954,-2.64787168,-1.81726906,-1.67104974,2.33762043,-4.30273117,0.4839841,-1.28253034,-10.6704077,-0.7641103,-3.58493721,2.07283886,0.08385173,0.91461126]]
yhat = model.predict(row)
print('Predicted Class: %d' % yhat[0])

运行该示例使 AdaBoost 集成模型适合整个数据集，然后用于对新的数据行进行预测，就像我们在应用程序中使用该模型时可能做的那样。

Predicted Class: 0

既然我们已经熟悉了使用 AdaBoost 进行分类，那么让我们来看看回归的 API。

回归的 AdaBoost

在本节中，我们将研究使用 AdaBoost 解决回归问题。

首先，我们可以使用make _ revolution()函数创建一个包含 1000 个示例和 20 个输入特征的合成回归问题。

下面列出了完整的示例。

# test regression dataset
from sklearn.datasets import make_regression
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=6)
# summarize the dataset
print(X.shape, y.shape)

运行该示例将创建数据集并总结输入和输出组件的形状。

(1000, 20) (1000,)

接下来，我们可以在这个数据集上评估一个 AdaBoost 算法。

正如我们在上一节中所做的，我们将使用重复的 k-fold 交叉验证来评估模型，重复 3 次，重复 10 次。我们将报告所有重复和折叠模型的平均绝对误差(MAE)。Sklearn 库使 MAE 为负，因此它被最大化而不是最小化。这意味着负 MAE 越大越好，完美模型的 MAE 为 0。

下面列出了完整的示例。

# evaluate adaboost ensemble for regression
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.ensemble import AdaBoostRegressor
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=6)
# define the model
model = AdaBoostRegressor()
# evaluate the model
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('MAE: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到带有默认超参数的 AdaBoost 集成实现了大约 100 的 MAE。

MAE: -72.327 (4.041)

我们也可以使用 AdaBoost 模型作为最终模型，并对回归进行预测。

首先，AdaBoost 集成适合所有可用数据，然后可以调用 predict() 函数对新数据进行预测。

下面的例子在我们的回归数据集上演示了这一点。

# adaboost ensemble for making predictions for regression
from sklearn.datasets import make_regression
from sklearn.ensemble import AdaBoostRegressor
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=6)
# define the model
model = AdaBoostRegressor()
# fit the model on the whole dataset
model.fit(X, y)
# make a single prediction
row = [[1.20871625,0.88440466,-0.9030013,-0.22687731,-0.82940077,-1.14410988,1.26554256,-0.2842871,1.43929072,0.74250241,0.34035501,0.45363034,0.1778756,-1.75252881,-1.33337384,-1.50337215,-0.45099008,0.46160133,0.58385557,-1.79936198]]
yhat = model.predict(row)
print('Prediction: %d' % yhat[0])

运行该示例使 AdaBoost 集成模型适合整个数据集，然后用于对新的数据行进行预测，就像我们在应用程序中使用该模型时可能做的那样。

Prediction: -10

现在我们已经熟悉了使用 Sklearn API 来评估和使用 AdaBoost 集成，接下来让我们看看如何配置模型。

AdaBoost 超参数

在本节中，我们将仔细研究您应该考虑为 AdaBoost 集成调整的一些超参数及其对模型表现的影响。

探索树的数量

AdaBoost 算法的一个重要超参数是集成中使用的决策树的数量。

回想一下，集成中使用的每个决策树都是为弱学习器设计的。也就是说，它比随机预测有技巧，但技巧性不高。因此，使用了一级决策树，称为决策树桩。

添加到模型中的树的数量必须很高，模型才能很好地工作，通常是几百棵树，如果不是几千棵树的话。

树的数量可以通过“n _ estimates”参数设置，默认为 50。

下面的示例探讨了值在 10 到 5，000 之间的树的数量的影响。

# explore adaboost ensemble number of trees effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import AdaBoostClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	# define number of trees to consider
	n_trees = [10, 50, 100, 500, 1000, 5000]
	for n in n_trees:
		models[str(n)] = AdaBoostClassifier(n_estimators=n)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
	# define the evaluation procedure
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model and collect the results
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	# evaluate the model
	scores = evaluate_model(model, X, y)
	# store the results
	results.append(scores)
	names.append(name)
	# summarize the performance along the way
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

运行该示例首先报告每个配置数量的决策树的平均准确性。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到这个数据集上的表现提高了，直到大约 50 棵树，然后下降。这可能是在添加额外树之后，集合过拟合训练数据集的迹象。

>10 0.773 (0.039)
>50 0.806 (0.041)
>100 0.801 (0.032)
>500 0.793 (0.028)
>1000 0.791 (0.032)
>5000 0.782 (0.031)

为每个配置数量的树的准确度分数的分布创建一个方框和须图。

我们可以看到模型表现和集合大小的总体趋势。

AdaBoost 集成大小与分类准确率的箱线图

探索弱势学习器

默认情况下，具有一个级别的决策树被用作弱学习器。

通过增加决策树的深度，我们可以使集成中使用的模型不那么弱(更熟练)。

下面的例子探索了增加决策树分类器弱学习器的深度对 AdBoost 集成的影响。

# explore adaboost ensemble tree depth effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	# explore depths from 1 to 10
	for i in range(1,11):
		# define base model
		base = DecisionTreeClassifier(max_depth=i)
		# define ensemble model
		models[str(i)] = AdaBoostClassifier(base_estimator=base)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
	# define the evaluation procedure
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model and collect the results
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	# evaluate the model
	scores = evaluate_model(model, X, y)
	# store the results
	results.append(scores)
	names.append(name)
	# summarize the performance along the way
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

运行该示例首先报告每个配置的弱学习器树深度的平均准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到，随着决策树深度的增加，集成的表现在这个数据集上也增加了。

>1 0.806 (0.041)
>2 0.864 (0.028)
>3 0.867 (0.030)
>4 0.889 (0.029)
>5 0.909 (0.021)
>6 0.923 (0.020)
>7 0.927 (0.025)
>8 0.928 (0.028)
>9 0.923 (0.017)
>10 0.926 (0.030)

为每个已配置的弱学习器深度的准确度分数分布创建一个方框和须图。

我们可以看到模型表现和弱学习器深度的总体趋势。

AdaBoost 集成弱学习器深度与分类准确率的箱线图

探索学习率

AdaBoost 还支持一个学习率，控制每个模型对集成预测的贡献。

这由“ learning_rate ”参数控制，默认设置为 1.0 或完全贡献。根据集合中使用的模型数量，较小或较大的值可能是合适的。在模型的贡献和集合中的树的数量之间有一个平衡。

更多的树可能需要更小的学习率；较少的树可能需要较大的学习率。通常使用 0 到 1 之间的值，有时使用非常小的值来避免过拟合，例如 0.1、0.01 或 0.001。

下面的示例以 0.1 为增量探索 0.1 到 2.0 之间的学习率值。

# explore adaboost ensemble learning rate effect on performance
from numpy import mean
from numpy import std
from numpy import arange
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import AdaBoostClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	# explore learning rates from 0.1 to 2 in 0.1 increments
	for i in arange(0.1, 2.1, 0.1):
		key = '%.3f' % i
		models[key] = AdaBoostClassifier(learning_rate=i)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
	# define the evaluation procedure
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model and collect the results
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	# evaluate the model
	scores = evaluate_model(model, X, y)
	# store the results
	results.append(scores)
	names.append(name)
	# summarize the performance along the way
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.xticks(rotation=45)
pyplot.show()

运行示例首先报告每个配置的学习率的平均准确性。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到 0.5 到 1.0 之间的相似值，以及之后模型表现的下降。

>0.100 0.767 (0.049)
>0.200 0.786 (0.042)
>0.300 0.802 (0.040)
>0.400 0.798 (0.037)
>0.500 0.805 (0.042)
>0.600 0.795 (0.031)
>0.700 0.799 (0.035)
>0.800 0.801 (0.033)
>0.900 0.805 (0.032)
>1.000 0.806 (0.041)
>1.100 0.801 (0.037)
>1.200 0.800 (0.030)
>1.300 0.799 (0.041)
>1.400 0.793 (0.041)
>1.500 0.790 (0.040)
>1.600 0.775 (0.034)
>1.700 0.767 (0.054)
>1.800 0.768 (0.040)
>1.900 0.736 (0.047)
>2.000 0.682 (0.048)

为每个配置的学习率的准确度分数的分布创建一个方框和须图。

在这个数据集上，我们可以看到学习率大于 1.0 时模型表现下降的总体趋势。

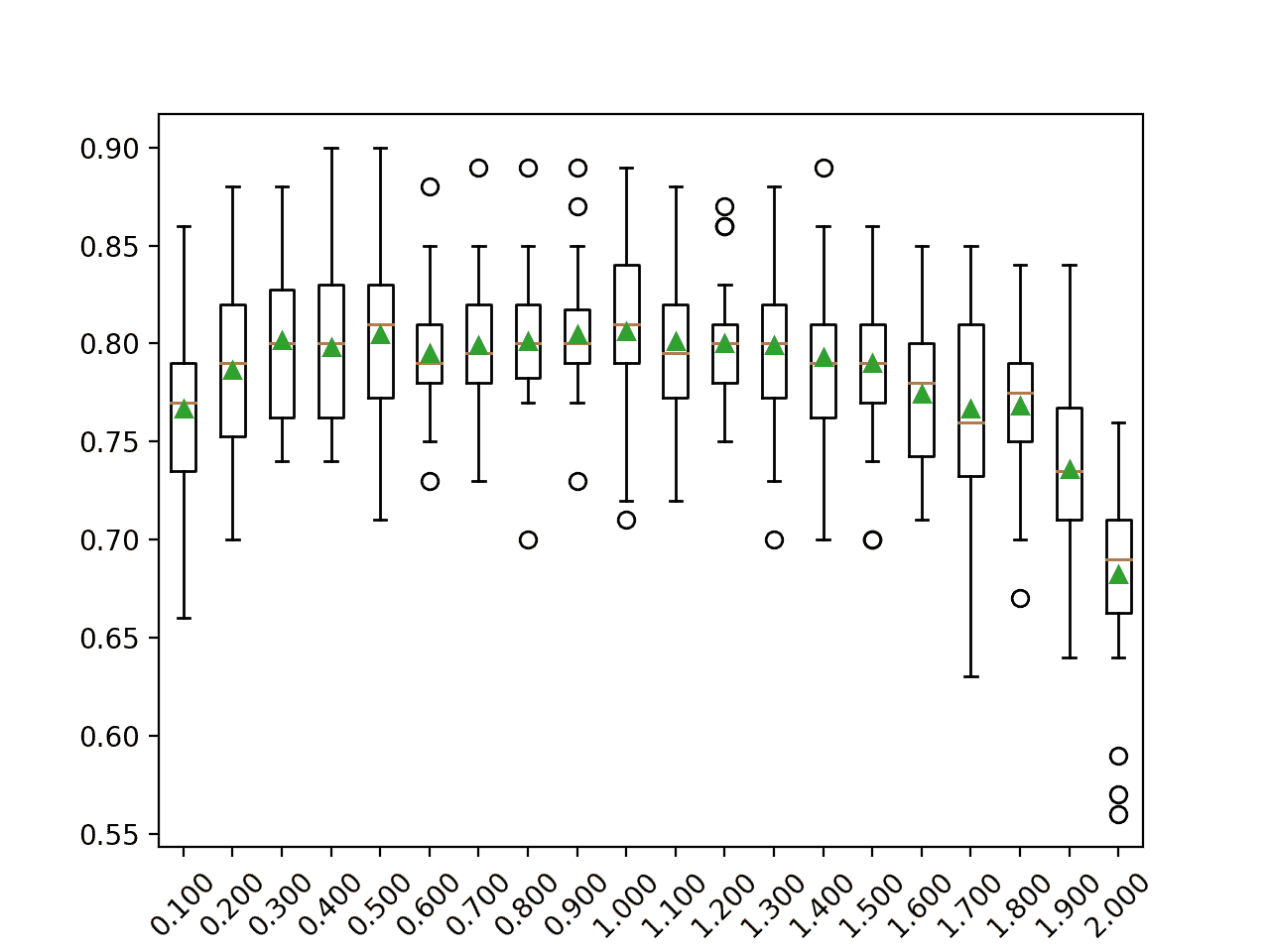
AdaBoost 集成学习率与分类准确率的箱线图

探索替代算法

集成中使用的默认算法是决策树，尽管也可以使用其他算法。

目的是使用非常简单的模型，称为弱学习器。此外，Sklearn 实现要求使用的任何模型也必须支持加权样本，因为它们是如何通过基于训练数据集的加权版本拟合模型来创建集成的。

可以通过“ base_estimator ”参数指定基础模型。在分类的情况下，基础模型还必须支持预测概率或类似概率的分数。如果指定的模型不支持加权训练数据集，您将看到如下错误消息:

ValueError: KNeighborsClassifier doesn't support sample_weight.

支持加权训练的模型的一个例子是逻辑回归算法。

下面的例子演示了一个带有弱学习器的 AdaBoost 算法。

# evaluate adaboost algorithm with logistic regression weak learner for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import AdaBoostClassifier
from sklearn.linear_model import LogisticRegression
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
# define the model
model = AdaBoostClassifier(base_estimator=LogisticRegression())
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到带有逻辑回归弱模型的 AdaBoost 集成在这个测试数据集上实现了大约 79%的分类准确率。

Accuracy: 0.794 (0.032)

网格搜索 AdaBoost 超参数

将 AdaBoost 配置为算法可能具有挑战性，因为许多影响模型在训练数据上的行为的关键超参数和超参数相互作用。

因此，使用搜索过程来发现模型超参数的配置是一个好的实践，该配置对于给定的预测建模问题是有效的或最好的。流行的搜索过程包括随机搜索和网格搜索。

在这一节中，我们将研究 AdaBoost 算法的关键超参数的网格搜索公共范围，您可以将其用作自己项目的起点。这可以通过使用 GridSearchCV 类并指定将模型超参数名称映射到要搜索的值的字典来实现。

在这种情况下，我们将网格搜索 AdaBoost 的两个关键超参数:集成中使用的树的数量和学习率。我们将为每个超参数使用一系列流行的表现良好的值。

每个配置组合将使用重复的 k 倍交叉验证进行评估，配置将使用平均得分进行比较，在这种情况下，使用分类准确率。

下面列出了在我们的合成类别数据集上网格搜索 AdaBoost 算法的关键超参数的完整示例。

# example of grid searching key hyperparameters for adaboost on a classification dataset
from sklearn.datasets import make_classification
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import AdaBoostClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=6)
# define the model with default hyperparameters
model = AdaBoostClassifier()
# define the grid of values to search
grid = dict()
grid['n_estimators'] = [10, 50, 100, 500]
grid['learning_rate'] = [0.0001, 0.001, 0.01, 0.1, 1.0]
# define the evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# define the grid search procedure
grid_search = GridSearchCV(estimator=model, param_grid=grid, n_jobs=-1, cv=cv, scoring='accuracy')
# execute the grid search
grid_result = grid_search.fit(X, y)
# summarize the best score and configuration
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
# summarize all scores that were evaluated
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
    print("%f (%f) with: %r" % (mean, stdev, param))

运行该示例可能需要一段时间，具体取决于您的硬件。在运行结束时，首先报告获得最佳分数的配置，然后是所考虑的所有其他配置的分数。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到具有 500 棵树和 0.1 学习率的配置表现最好，分类准确率约为 81.3%。

尽管在这种情况下没有测试这些配置，以确保网格搜索在合理的时间内完成，但该模型在有更多树(如 1000 或 5000 棵树)的情况下可能会表现得更好。

Best: 0.813667 using {'learning_rate': 0.1, 'n_estimators': 500}
0.646333 (0.036376) with: {'learning_rate': 0.0001, 'n_estimators': 10}
0.646667 (0.036545) with: {'learning_rate': 0.0001, 'n_estimators': 50}
0.646667 (0.036545) with: {'learning_rate': 0.0001, 'n_estimators': 100}
0.647000 (0.038136) with: {'learning_rate': 0.0001, 'n_estimators': 500}
0.646667 (0.036545) with: {'learning_rate': 0.001, 'n_estimators': 10}
0.647000 (0.038136) with: {'learning_rate': 0.001, 'n_estimators': 50}
0.654333 (0.045511) with: {'learning_rate': 0.001, 'n_estimators': 100}
0.672667 (0.046543) with: {'learning_rate': 0.001, 'n_estimators': 500}
0.648333 (0.042197) with: {'learning_rate': 0.01, 'n_estimators': 10}
0.671667 (0.045613) with: {'learning_rate': 0.01, 'n_estimators': 50}
0.715000 (0.053213) with: {'learning_rate': 0.01, 'n_estimators': 100}
0.767667 (0.045948) with: {'learning_rate': 0.01, 'n_estimators': 500}
0.716667 (0.048876) with: {'learning_rate': 0.1, 'n_estimators': 10}
0.767000 (0.049271) with: {'learning_rate': 0.1, 'n_estimators': 50}
0.784667 (0.042874) with: {'learning_rate': 0.1, 'n_estimators': 100}
0.813667 (0.032092) with: {'learning_rate': 0.1, 'n_estimators': 500}
0.773333 (0.038759) with: {'learning_rate': 1.0, 'n_estimators': 10}
0.806333 (0.040701) with: {'learning_rate': 1.0, 'n_estimators': 50}
0.801000 (0.032491) with: {'learning_rate': 1.0, 'n_estimators': 100}
0.792667 (0.027560) with: {'learning_rate': 1.0, 'n_estimators': 500}

进一步阅读

如果您想更深入地了解这个主题，本节将提供更多资源。

教程

• 机器学习的 Boosting 和 AdaBoost】

报纸

• 在线学习的决策理论推广及其在提升中的应用，1996。
• 多级 AdaBoost ，2009。
• 使用增强技术改进回归器，1997。

蜜蜂

• 硬化。一起。AdaBoost gressier API。
• 硬化。一起。AdaBoost 分类 API 。

文章

• Boosting(机器学习)，维基百科。
• AdaBoost，维基百科。

摘要

在本教程中，您发现了如何开发用于分类和回归的 AdaBoost 集成。

具体来说，您了解到:

• AdaBoost 集成是从顺序添加到模型中的决策树创建的集成。
• 如何使用 AdaBoost 集成与 Sklearn 进行分类和回归。
• 如何探索 AdaBoost 模型超参数对模型表现的影响？

你有什么问题吗？
在下面的评论中提问，我会尽力回答。

使用不同数据转换开发装袋集成

原文：https://machinelearningmastery.com/bagging-ensemble-with-different-data-transformations/

最后更新于 2021 年 4 月 27 日

Bootstrap 聚合(或 bagging)是一种集成，其中每个模型都在训练数据集的不同样本上进行训练。

bagging 的思想可以推广到用于改变训练数据集和在数据的每个改变版本上拟合相同模型的其他技术。一种方法是使用改变输入变量的规模和概率分布的数据变换，作为训练类似 bagging 的集合的贡献成员的基础。我们可以称之为数据转换装袋或数据转换集成。

在本教程中，您将发现如何开发数据转换集成。

完成本教程后，您将知道:

• 数据转换可以用作 bagging 类型集成的基础，在 bagging 类型集成中，在训练数据集的不同视图上训练相同的模型。
• 如何开发一个用于分类的数据转换集成，并确认该集成的表现优于任何贡献成员。
• 如何开发和评估用于回归预测建模的数据转换集成？

用我的新书Python 集成学习算法启动你的项目，包括分步教程和所有示例的 Python 源代码文件。

我们开始吧。

开发具有不同数据转换的装袋集成
照片由麦克杰·克劳斯拍摄，保留部分权利。

教程概述

本教程分为三个部分；它们是:

1. 数据转换装袋
2. 用于分类的数据变换集成
3. 回归的数据变换集成

数据转换装袋

Bootstrap 聚合，简称 bagging，是一种集成学习技术，基于在同一训练数据集的多个不同样本上拟合相同模型类型的思想。

希望用于拟合每个模型的训练数据集的微小差异将导致模型能力的微小差异。对于集成学习，这被称为集成成员的多样性，并且旨在使每个贡献成员做出的预测(或预测误差)去相关。

尽管它被设计为与决策树一起使用，并且每个数据样本都是使用 bootstrap 方法(用 rel-selection 进行选择)制作的，但是该方法已经产生了一个完整的研究子领域，对该方法有数百种变体。

我们可以通过改变用于以新的和独特的方式训练每个贡献成员的数据集来构建我们自己的装袋集成。

一种方法是对每个有贡献的集合成员的数据集应用不同的数据准备转换。

这是基于这样一个前提，即我们不能知道将未知底层结构暴露给学习算法的数据集的训练数据集的表示形式。这激发了用一套不同的数据转换来评估模型的需求，例如改变比例和概率分布，以便发现什么是有效的。

这种方法可用于创建同一训练数据集的一组不同变换，对每个变换训练一个模型，并使用简单的统计(如平均)组合预测。

由于没有更好的名称，我们将其称为“数据转换装袋或“数据转换集成”

我们可以使用许多变换，但一个好的起点可能是改变规模和概率分布的选择，例如:

• 归一化(固定范围)
• 标准化(零均值)
• 稳健标准化(对异常值稳健)
• 电力变压器(消除歪斜)
• 分位数变换(变化分布)
• 离散化 (k 箱)

当与基于数据转换效果训练不同或非常不同模型的基础模型一起使用时，该方法可能更有效。

改变分布的比例可能只适用于对输入变量的比例变化敏感的模型，如计算加权和的模型，如逻辑回归和神经网络，以及使用距离度量的模型，如 k 近邻和支持向量机。

输入变量概率分布的变化可能会影响大多数机器学习模型。

现在我们已经熟悉了这种方法，让我们来探索如何为分类问题开发一个数据转换集成。

用于分类的数据变换集成

我们可以使用 Sklearn 库开发一种装袋分类的数据转换方法。

该库提供了一套我们可以直接使用的标准转换。每个集成成员可以被定义为一个管道，转换之后是预测模型，以避免任何数据泄漏，进而产生乐观的结果。最后，可以使用投票集合来组合来自每个管道的预测。

首先，我们可以定义一个合成的二进制类别数据集，作为探索这种类型集成的基础。

下面的示例创建了一个包含 1，000 个示例的数据集，每个示例包含 20 个输入要素，其中 15 个包含预测目标的信息。

# synthetic classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
# summarize the dataset
print(X.shape, y.shape)

运行该示例将创建数据集并总结数据数组的形状，这证实了我们的预期。

(1000, 20) (1000,)

接下来，我们使用我们打算在集合中使用的预测模型来建立问题的基线。标准做法是在装袋集成中使用决策树，因此在这种情况下，我们将使用带有默认超参数的决策树分类器。

我们将使用标准实践来评估模型，在这种情况下，使用三次重复和 10 次重复的重复分层 k-fold 交叉验证。将使用所有折叠和重复的分类准确度的平均值来报告表现。

下面列出了在综合类别数据集上评估决策树的完整示例。

# evaluate decision tree on synthetic classification dataset
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.tree import DecisionTreeClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
# define the model
model = DecisionTreeClassifier()
# define the evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report performance
print('Mean Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例报告了决策树在合成类别数据集上的平均分类准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到该模型实现了大约 82.3%的分类准确率。

这个分数提供了一个表现基线，我们期望数据转换集成能够在此基础上有所改进。

Mean Accuracy: 0.823 (0.039)

接下来，我们可以开发一组决策树，每一个都适合输入数据的不同变换。

首先，我们可以将每个集成成员定义为一个建模管道。第一步是数据转换，第二步是决策树分类器。

例如，带有最小最大缩放器类的规范化转换的管道如下所示:

...
# normalization
norm = Pipeline([('s', MinMaxScaler()), ('m', DecisionTreeClassifier())])

对于我们想要使用的每个转换或转换配置，我们可以重复这一过程，并将所有模型管道添加到列表中。

VotingClassifier 类可用于组合所有模型的预测。这个类接受一个“估值器”参数，它是一个元组列表，其中每个元组都有一个名称和模型或建模管道。例如:

...
# normalization
norm = Pipeline([('s', MinMaxScaler()), ('m', DecisionTreeClassifier())])
models.append(('norm', norm))
...
# define the voting ensemble
ensemble = VotingClassifier(estimators=models, voting='hard')

为了使代码更容易阅读，我们可以定义一个函数 get_ensemble() 来创建成员和数据转换 ensemble 本身。

# get a voting ensemble of models
def get_ensemble():
	# define the base models
	models = list()
	# normalization
	norm = Pipeline([('s', MinMaxScaler()), ('m', DecisionTreeClassifier())])
	models.append(('norm', norm))
	# standardization
	std = Pipeline([('s', StandardScaler()), ('m', DecisionTreeClassifier())])
	models.append(('std', std))
	# robust
	robust = Pipeline([('s', RobustScaler()), ('m', DecisionTreeClassifier())])
	models.append(('robust', robust))
	# power
	power = Pipeline([('s', PowerTransformer()), ('m', DecisionTreeClassifier())])
	models.append(('power', power))
	# quantile
	quant = Pipeline([('s', QuantileTransformer(n_quantiles=100, output_distribution='normal')), ('m', DecisionTreeClassifier())])
	models.append(('quant', quant))
	# kbins
	kbins = Pipeline([('s', KBinsDiscretizer(n_bins=20, encode='ordinal')), ('m', DecisionTreeClassifier())])
	models.append(('kbins', kbins))
	# define the voting ensemble
	ensemble = VotingClassifier(estimators=models, voting='hard')
	return ensemble

然后，我们可以调用这个函数，并按照正常方式评估投票集合，就像我们对上面的决策树所做的那样。

将这些联系在一起，完整的示例如下所示。

# evaluate data transform bagging ensemble on a classification dataset
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import PowerTransformer
from sklearn.preprocessing import QuantileTransformer
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.pipeline import Pipeline

# get a voting ensemble of models
def get_ensemble():
	# define the base models
	models = list()
	# normalization
	norm = Pipeline([('s', MinMaxScaler()), ('m', DecisionTreeClassifier())])
	models.append(('norm', norm))
	# standardization
	std = Pipeline([('s', StandardScaler()), ('m', DecisionTreeClassifier())])
	models.append(('std', std))
	# robust
	robust = Pipeline([('s', RobustScaler()), ('m', DecisionTreeClassifier())])
	models.append(('robust', robust))
	# power
	power = Pipeline([('s', PowerTransformer()), ('m', DecisionTreeClassifier())])
	models.append(('power', power))
	# quantile
	quant = Pipeline([('s', QuantileTransformer(n_quantiles=100, output_distribution='normal')), ('m', DecisionTreeClassifier())])
	models.append(('quant', quant))
	# kbins
	kbins = Pipeline([('s', KBinsDiscretizer(n_bins=20, encode='ordinal')), ('m', DecisionTreeClassifier())])
	models.append(('kbins', kbins))
	# define the voting ensemble
	ensemble = VotingClassifier(estimators=models, voting='hard')
	return ensemble

# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
# get models
ensemble = get_ensemble()
# define the evaluation procedure
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model
n_scores = cross_val_score(ensemble, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
# report performance
print('Mean Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例报告了数据变换集合在合成类别数据集上的平均分类准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到数据转换集成实现了大约 83.8%的分类准确率，这比单独使用决策树实现了大约 82.3%的准确率有所提升。

Mean Accuracy: 0.838 (0.042)

尽管与单个决策树相比，该集成表现良好，但该测试的一个限制是，我们不知道该集成是否比任何贡献成员表现更好。

这很重要，因为如果一个贡献的成员表现得更好，那么使用成员本身作为模型而不是整体会更简单和容易。

我们可以通过评估每个单独模型的表现并将结果与整体进行比较来检查这一点。

首先，我们可以更新 get_ensemble() 函数，返回一个由单个集成成员以及集成本身组成的待评估模型列表。

# get a voting ensemble of models
def get_ensemble():
	# define the base models
	models = list()
	# normalization
	norm = Pipeline([('s', MinMaxScaler()), ('m', DecisionTreeClassifier())])
	models.append(('norm', norm))
	# standardization
	std = Pipeline([('s', StandardScaler()), ('m', DecisionTreeClassifier())])
	models.append(('std', std))
	# robust
	robust = Pipeline([('s', RobustScaler()), ('m', DecisionTreeClassifier())])
	models.append(('robust', robust))
	# power
	power = Pipeline([('s', PowerTransformer()), ('m', DecisionTreeClassifier())])
	models.append(('power', power))
	# quantile
	quant = Pipeline([('s', QuantileTransformer(n_quantiles=100, output_distribution='normal')), ('m', DecisionTreeClassifier())])
	models.append(('quant', quant))
	# kbins
	kbins = Pipeline([('s', KBinsDiscretizer(n_bins=20, encode='ordinal')), ('m', DecisionTreeClassifier())])
	models.append(('kbins', kbins))
	# define the voting ensemble
	ensemble = VotingClassifier(estimators=models, voting='hard')
	# return a list of tuples each with a name and model
	return models + [('ensemble', ensemble)]

我们可以调用这个函数，枚举每个模型，评估它，报告表现，并存储结果。

...
# get models
models = get_ensemble()
# evaluate each model
results = list()
for name,model in models:
	# define the evaluation method
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model on the dataset
	n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	# report performance
	print('>%s: %.3f (%.3f)' % (name, mean(n_scores), std(n_scores)))
	results.append(n_scores)

最后，我们可以将准确度分数的分布绘制为并排的方框图和触须图，并直接比较分数的分布。

从视觉上看，我们希望整体分数的分布比任何单个成员都偏高，并且分布的中心趋势(平均值和中值)也比任何成员都高。

...
# plot the results for comparison
pyplot.boxplot(results, labels=[n for n,_ in models], showmeans=True)
pyplot.show()

将这些联系在一起，下面列出了将贡献成员的表现与数据转换集成的表现进行比较的完整示例。

# comparison of data transform ensemble to each contributing member for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import PowerTransformer
from sklearn.preprocessing import QuantileTransformer
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.pipeline import Pipeline
from matplotlib import pyplot

# get a voting ensemble of models
def get_ensemble():
	# define the base models
	models = list()
	# normalization
	norm = Pipeline([('s', MinMaxScaler()), ('m', DecisionTreeClassifier())])
	models.append(('norm', norm))
	# standardization
	std = Pipeline([('s', StandardScaler()), ('m', DecisionTreeClassifier())])
	models.append(('std', std))
	# robust
	robust = Pipeline([('s', RobustScaler()), ('m', DecisionTreeClassifier())])
	models.append(('robust', robust))
	# power
	power = Pipeline([('s', PowerTransformer()), ('m', DecisionTreeClassifier())])
	models.append(('power', power))
	# quantile
	quant = Pipeline([('s', QuantileTransformer(n_quantiles=100, output_distribution='normal')), ('m', DecisionTreeClassifier())])
	models.append(('quant', quant))
	# kbins
	kbins = Pipeline([('s', KBinsDiscretizer(n_bins=20, encode='ordinal')), ('m', DecisionTreeClassifier())])
	models.append(('kbins', kbins))
	# define the voting ensemble
	ensemble = VotingClassifier(estimators=models, voting='hard')
	# return a list of tuples each with a name and model
	return models + [('ensemble', ensemble)]

# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
# get models
models = get_ensemble()
# evaluate each model
results = list()
for name,model in models:
	# define the evaluation method
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model on the dataset
	n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	# report performance
	print('>%s: %.3f (%.3f)' % (name, mean(n_scores), std(n_scores)))
	results.append(n_scores)
# plot the results for comparison
pyplot.boxplot(results, labels=[n for n,_ in models], showmeans=True)
pyplot.show()

运行该示例首先报告每个单独模型的平均和标准分类准确率，最后是组合模型的集成的表现。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到许多单个成员表现良好，例如准确率约为 83.3%的“T0”kbins，准确率约为 83.1%的“T2”STD。我们还可以看到，与任何贡献成员相比，该集成实现了更好的整体表现，准确率约为 83.4%。

>norm: 0.821 (0.041)
>std: 0.831 (0.045)
>robust: 0.826 (0.044)
>power: 0.825 (0.045)
>quant: 0.817 (0.042)
>kbins: 0.833 (0.035)
>ensemble: 0.834 (0.040)

还创建了一个图形，显示了每个单独模型以及数据转换集合的分类准确率的方框图和触须图。

我们可以看到集成的分布是向上倾斜的，这是我们可能希望的，并且平均值(绿色三角形)略高于单个集成成员的平均值。

单个模型和数据转换集合准确率分布的盒须图

既然我们已经熟悉了如何开发一个用于分类的数据转换集成，那么让我们看看如何对回归做同样的事情。

回归的数据变换集成

在本节中，我们将探索为回归预测建模问题开发数据转换集成。

首先，我们可以定义一个合成的二元回归数据集作为探索这种类型集成的基础。

下面的示例创建了一个数据集，其中 100 个输入要素各有 1，000 个示例，其中 10 个包含预测目标的信息。

# synthetic regression dataset
from sklearn.datasets import make_regression
# define dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1, random_state=1)
# summarize the dataset
print(X.shape, y.shape)

运行该示例将创建数据集，并确认数据具有预期的形状。

(1000, 100) (1000,)

接下来，我们可以通过拟合和评估我们打算在集成中使用的基础模型来建立合成数据集的表现基线，在本例中，基础模型是决策树回归器。

该模型将使用重复的 k-fold 交叉验证进行评估，重复 3 次，重复 10 次。数据集上的模型表现将使用平均绝对误差(MAE)报告。Sklearn 将反转分数(使其为负数)，以便框架可以最大化分数。因此，我们可以忽略分数上的符号。

下面的示例评估了合成回归数据集上的决策树。

# evaluate decision tree on synthetic regression dataset
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.tree import DecisionTreeRegressor
# define dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1, random_state=1)
# define the model
model = DecisionTreeRegressor()
# define the evaluation procedure
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
# evaluate the model
n_scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1)
# report performance
print('MAE: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告合成回归数据集上决策树的 MAE。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到模型实现了大约 139.817 的 MAE。这提供了一个我们期望集合模型改进的表现下限。

MAE: -139.817 (12.449)

接下来，我们可以开发和评估该集成。

我们将使用与上一节相同的数据转换。将使用voting returnalizer来组合预测，这适用于回归问题。

下面定义的 get_ensemble()函数创建单个模型和集成模型，并将所有模型组合成元组列表进行评估。

# get a voting ensemble of models
def get_ensemble():
	# define the base models
	models = list()
	# normalization
	norm = Pipeline([('s', MinMaxScaler()), ('m', DecisionTreeRegressor())])
	models.append(('norm', norm))
	# standardization
	std = Pipeline([('s', StandardScaler()), ('m', DecisionTreeRegressor())])
	models.append(('std', std))
	# robust
	robust = Pipeline([('s', RobustScaler()), ('m', DecisionTreeRegressor())])
	models.append(('robust', robust))
	# power
	power = Pipeline([('s', PowerTransformer()), ('m', DecisionTreeRegressor())])
	models.append(('power', power))
	# quantile
	quant = Pipeline([('s', QuantileTransformer(n_quantiles=100, output_distribution='normal')), ('m', DecisionTreeRegressor())])
	models.append(('quant', quant))
	# kbins
	kbins = Pipeline([('s', KBinsDiscretizer(n_bins=20, encode='ordinal')), ('m', DecisionTreeRegressor())])
	models.append(('kbins', kbins))
	# define the voting ensemble
	ensemble = VotingRegressor(estimators=models)
	# return a list of tuples each with a name and model
	return models + [('ensemble', ensemble)]

然后，我们可以调用这个函数，独立评估每个有贡献的建模管道，并将结果与管道的总体进行比较。

和以前一样，我们的期望是，集成会提升任何单个模型的表现。如果没有，那么应该选择表现最好的个人模型。

将这些联系在一起，下面列出了评估回归数据集的数据转换集成的完整示例。

# comparison of data transform ensemble to each contributing member for regression
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import PowerTransformer
from sklearn.preprocessing import QuantileTransformer
from sklearn.preprocessing import KBinsDiscretizer
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import VotingRegressor
from sklearn.pipeline import Pipeline
from matplotlib import pyplot

# get a voting ensemble of models
def get_ensemble():
	# define the base models
	models = list()
	# normalization
	norm = Pipeline([('s', MinMaxScaler()), ('m', DecisionTreeRegressor())])
	models.append(('norm', norm))
	# standardization
	std = Pipeline([('s', StandardScaler()), ('m', DecisionTreeRegressor())])
	models.append(('std', std))
	# robust
	robust = Pipeline([('s', RobustScaler()), ('m', DecisionTreeRegressor())])
	models.append(('robust', robust))
	# power
	power = Pipeline([('s', PowerTransformer()), ('m', DecisionTreeRegressor())])
	models.append(('power', power))
	# quantile
	quant = Pipeline([('s', QuantileTransformer(n_quantiles=100, output_distribution='normal')), ('m', DecisionTreeRegressor())])
	models.append(('quant', quant))
	# kbins
	kbins = Pipeline([('s', KBinsDiscretizer(n_bins=20, encode='ordinal')), ('m', DecisionTreeRegressor())])
	models.append(('kbins', kbins))
	# define the voting ensemble
	ensemble = VotingRegressor(estimators=models)
	# return a list of tuples each with a name and model
	return models + [('ensemble', ensemble)]

# generate regression dataset
X, y = make_regression(n_samples=1000, n_features=100, n_informative=10, noise=0.1, random_state=1)
# get models
models = get_ensemble()
# evaluate each model
results = list()
for name,model in models:
	# define the evaluation method
	cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model on the dataset
	n_scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1)
	# report performance
	print('>%s: %.3f (%.3f)' % (name, mean(n_scores), std(n_scores)))
	results.append(n_scores)
# plot the results for comparison
pyplot.boxplot(results, labels=[n for n,_ in models], showmeans=True)
pyplot.show()

运行该示例首先报告每个单独模型的 MAE，最后是组合模型的集合的表现。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

我们可以看到，每个模型的表现都差不多，MAE 误差分数在 140 左右，都高于孤立使用的决策树。有趣的是，该集成表现最好，超过了所有单个成员和没有变换的树，达到了大约 126.487 的 MAE。

这个结果表明，虽然每个管道的表现比没有转换的单个树差，但是每个管道都产生不同的错误，并且模型的平均值能够利用这些差异来降低错误。

>norm: -140.559 (11.783)
>std: -140.582 (11.996)
>robust: -140.813 (11.827)
>power: -141.089 (12.668)
>quant: -141.109 (11.097)
>kbins: -145.134 (11.638)
>ensemble: -126.487 (9.999)

创建一个图形，比较每个管道和集合的 MAE 分数分布。

正如我们所希望的，与所有其他模型相比，集合的分布偏斜度更高，并且具有更高(更小)的中心趋势(分别由绿色三角形和橙色线表示的平均值和中值)。

单个模型和数据转换集合的 MAE 分布的盒须图

进一步阅读

如果您想更深入地了解这个主题，本节将提供更多资源。

教程

• 如何用 Python 开发投票集成

书

• 使用集成方法的模式分类，2010。
• 集成方法，2012。
• 集成机器学习，2012。

蜜蜂

• 硬化。一起。投票分类器 API 。
• 硬化。一起。投票输入 API 。

摘要

在本教程中，您发现了如何开发数据转换集成。

具体来说，您了解到:

• 数据转换可以用作 bagging 类型集成的基础，在 bagging 类型集成中，在训练数据集的不同视图上训练相同的模型。
• 如何开发一个用于分类的数据转换集成，并确认该集成的表现优于任何贡献成员。
• 如何开发和评估用于回归预测建模的数据转换集成？

你有什么问题吗？
在下面的评论中提问，我会尽力回答。

如何用 Python 开发装袋集成

原文：https://machinelearningmastery.com/bagging-ensemble-with-python/

最后更新于 2021 年 4 月 27 日

Bagging 是一种集成机器学习算法，它结合了来自许多决策树的预测。

它也很容易实现，因为它只有很少的关键超参数和合理的试探法来配置这些超参数。

Bagging 总体上表现良好，并为决策树算法的整个集成领域提供了基础，例如流行的随机森林和额外树集成算法，以及不太为人知的粘贴、随机子空间和随机面片集成算法。

在本教程中，您将发现如何为分类和回归开发 Bagging 集成。

完成本教程后，您将知道:

• Bagging 集成是从适合数据集不同样本的决策树创建的集成。
• 如何用 Sklearn 使用 Bagging 集成进行分类和回归。
• 如何探索 Bagging 模型超参数对模型表现的影响。

用我的新书Python 集成学习算法启动你的项目，包括分步教程和所有示例的 Python 源代码文件。

我们开始吧。

• 更新 2020 年 8 月:增加了常见问题部分。

如何用 Python 开发装袋集成
图片由达文宁提供，保留部分权利。

教程概述

本教程分为五个部分；它们是:

1. 装袋集成算法
2. 装袋科学工具包-学习应用编程接口
   1. 分类装袋
   2. 回归装袋
3. 装袋超参数
   1. 探索树的数量
   2. 探索样本数量
   3. 探索替代算法
4. 装袋扩展
   1. 粘贴集成
   2. 随机子空间集成
   3. 随机面片集合
5. 常见问题

装袋集成算法

Bootstrap Aggregation，简称 Bagging，是一种集成机器学习算法。

具体来说，它是决策树模型的集合，尽管 bagging 技术也可以用于组合其他类型模型的预测。

顾名思义，bootstrap 聚合基于“ bootstrap ”样本的思想。

一个引导样本是一个带有替换的数据集样本。替换意味着从数据集中提取的样本被替换，允许它在新样本中被再次选择，也可能被多次选择。这意味着样本可能有来自原始数据集的重复示例。

自举采样技术用于从小数据样本中估计总体统计量。这是通过抽取多个自举样本，计算每个样本的统计量，并报告所有样本的平均统计量来实现的。

使用自举采样的一个例子是从一个小数据集中估计总体平均值。从数据集中抽取多个自举样本，计算每个样本的平均值，然后将估计平均值的平均值报告为总体的估计值。

令人惊讶的是，与原始数据集上的单一估计相比，自举方法提供了一种稳健且准确的统计量估计方法。

同样的方法可以用来创建决策树模型的集合。

这是通过从训练数据集中抽取多个引导样本并在每个样本上拟合决策树来实现的。来自决策树的预测然后被组合，以提供比单个决策树(典型地，但不总是)更稳健和准确的预测。

装袋预测器是一种生成预测器的多个版本并使用这些版本获得聚合预测器的方法。[……]多个版本是通过对学习集进行引导复制并将其用作新的学习集而形成的

——装袋预测因子，1996。

对回归问题的预测是通过对决策树中的预测取平均值来进行的。通过在决策树所做的预测中对类别进行多数票预测，来对分类问题进行预测。

袋装决策树是有效的，因为每个决策树都适合于稍微不同的训练数据集，这反过来允许每个树有微小的差异，并做出稍微不同的巧妙预测。

从技术上讲，我们说这种方法是有效的，因为这些树在预测之间的相关性很低，反过来，预测误差也很低。

使用决策树，特别是未运行的决策树，因为它们略微超出了训练数据，并且具有较高的方差。可以使用其他高方差机器学习算法，例如具有低的 k 值的 k 最近邻算法，尽管决策树已经被证明是最有效的。

如果扰动学习集会导致构建的预测器发生显著变化，那么装袋可以提高准确性。

——装袋预测因子，1996。

装袋并不总是能带来改善。对于已经表现良好的低方差模型，装袋会导致模型表现下降。

实验和理论证据都表明，装袋可以将一个好的但不稳定的过程推向最优化的重要一步。另一方面，它会稍微降低稳定程序的表现。

——装袋预测因子，1996。

装袋科学工具包-学习应用编程接口

装袋集成可以从零开始实现，尽管这对初学者来说很有挑战性。

有关示例，请参见教程:

• 如何用 Python 实现从零开始装袋

Sklearn Python 机器学习库为机器学习提供了 Bagging 集成的实现。

它有现代版本的图书馆。

首先，通过运行以下脚本来确认您使用的是现代版本的库:

# check Sklearn version
import sklearn
print(sklearn.__version__)

运行脚本将打印您的 Sklearn 版本。

您的版本应该相同或更高。如果没有，您必须升级 Sklearn 库的版本。

0.22.1

装袋通过装袋分类器和装袋分类器类提供。

这两个模型以相同的方式运行，并采用相同的参数来影响决策树的创建。

随机性用于模型的构建。这意味着算法每次在相同的数据上运行时，都会产生稍微不同的模型。

当使用具有随机学习算法的机器学习算法时，最好通过在多次运行或重复交叉验证中平均它们的表现来评估它们。当拟合最终模型时，可能需要增加树的数量，直到模型的方差在重复评估中减小，或者拟合多个最终模型并对它们的预测进行平均。

让我们看看如何为分类和回归开发一个 Bagging 集成。

分类装袋

在本节中，我们将研究如何使用 Bagging 解决分类问题。

首先，我们可以使用 make_classification()函数创建一个包含 1000 个示例和 20 个输入特征的合成二进制分类问题。

下面列出了完整的示例。

# test classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# summarize the dataset
print(X.shape, y.shape)

运行该示例将创建数据集并总结输入和输出组件的形状。

(1000, 20) (1000,)

接下来，我们可以在这个数据集上评估 Bagging 算法。

我们将使用重复分层 k 折叠交叉验证来评估模型，重复 3 次，折叠 10 次。我们将报告所有重复和折叠的模型准确率的平均值和标准偏差。

# evaluate bagging algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier()
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到具有默认超参数的 Bagging 集成在这个测试数据集上实现了大约 85%的分类准确率。

Accuracy: 0.856 (0.037)

我们也可以使用 Bagging 模型作为最终模型，并对分类进行预测。

首先，Bagging 集成适合所有可用数据，然后可以调用 predict() 函数对新数据进行预测。

下面的示例在我们的二进制类别数据集上演示了这一点。

# make predictions using bagging for classification
from sklearn.datasets import make_classification
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier()
# fit the model on the whole dataset
model.fit(X, y)
# make a single prediction
row = [[-4.7705504,-1.88685058,-0.96057964,2.53850317,-6.5843005,3.45711663,-7.46225013,2.01338213,-0.45086384,-1.89314931,-2.90675203,-0.21214568,-0.9623956,3.93862591,0.06276375,0.33964269,4.0835676,1.31423977,-2.17983117,3.1047287]]
yhat = model.predict(row)
print('Predicted Class: %d' % yhat[0])

运行该示例使 Bagging 集成模型适合整个数据集，然后用于对新的数据行进行预测，就像我们在应用程序中使用该模型时可能做的那样。

Predicted Class: 1

现在我们已经熟悉了使用 Bagging 进行分类，让我们看看回归的 API。

回归装袋

在这一节中，我们将研究使用 Bagging 解决回归问题。

首先，我们可以使用make _ revolution()函数创建一个包含 1000 个示例和 20 个输入特征的合成回归问题。

下面列出了完整的示例。

# test regression dataset
from sklearn.datasets import make_regression
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5)
# summarize the dataset
print(X.shape, y.shape)

运行该示例将创建数据集并总结输入和输出组件的形状。

(1000, 20) (1000,)

接下来，我们可以在这个数据集上评估 Bagging 算法。

正如我们在上一节中所做的，我们将使用重复的 k-fold 交叉验证来评估模型，重复 3 次，重复 10 次。我们将报告所有重复和折叠模型的平均绝对误差(MAE)。Sklearn 库使 MAE 为负，因此它被最大化而不是最小化。这意味着负 MAE 越大越好，完美模型的 MAE 为 0。

下面列出了完整的示例。

# evaluate bagging ensemble for regression
from numpy import mean
from numpy import std
from sklearn.datasets import make_regression
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.ensemble import BaggingRegressor
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5)
# define the model
model = BaggingRegressor()
# evaluate the model
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('MAE: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到具有默认超参数的 Bagging 集成实现了大约 100 的 MAE。

MAE: -101.133 (9.757)

我们也可以使用 Bagging 模型作为最终模型，并对回归进行预测。

首先，Bagging 集成适合所有可用数据，然后可以调用 predict() 函数对新数据进行预测。

下面的例子在我们的回归数据集上演示了这一点。

# bagging ensemble for making predictions for regression
from sklearn.datasets import make_regression
from sklearn.ensemble import BaggingRegressor
# define dataset
X, y = make_regression(n_samples=1000, n_features=20, n_informative=15, noise=0.1, random_state=5)
# define the model
model = BaggingRegressor()
# fit the model on the whole dataset
model.fit(X, y)
# make a single prediction
row = [[0.88950817,-0.93540416,0.08392824,0.26438806,-0.52828711,-1.21102238,-0.4499934,1.47392391,-0.19737726,-0.22252503,0.02307668,0.26953276,0.03572757,-0.51606983,-0.39937452,1.8121736,-0.00775917,-0.02514283,-0.76089365,1.58692212]]
yhat = model.predict(row)
print('Prediction: %d' % yhat[0])

运行该示例使 Bagging 集成模型适合整个数据集，然后用于对新的数据行进行预测，就像我们在应用程序中使用该模型时可能做的那样。

Prediction: -134

现在我们已经熟悉了使用 Sklearn API 来评估和使用 Bagging 集成，让我们来看看如何配置模型。

装袋超参数

在本节中，我们将仔细研究一些您应该考虑为 Bagging 集成进行调整的超参数，以及它们对模型表现的影响。

探索树的数量

Bagging 算法的一个重要超参数是集成中使用的决策树的数量。

通常，树的数量会增加，直到模型表现稳定下来。直觉可能暗示更多的树会导致过拟合，尽管事实并非如此。给定学习算法的随机性质，装袋和决策树算法的相关集成(如随机森林)似乎在某种程度上不会过拟合训练数据集。

树的数量可以通过“n _ estimates”参数设置，默认为 100。

下面的示例探讨了值在 10 到 5，000 之间的树的数量的影响。

# explore bagging ensemble number of trees effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	# define number of trees to consider
	n_trees = [10, 50, 100, 500, 500, 1000, 5000]
	for n in n_trees:
		models[str(n)] = BaggingClassifier(n_estimators=n)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
	# define the evaluation procedure
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model and collect the results
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	# evaluate the model
	scores = evaluate_model(model, X, y)
	# store the results
	results.append(scores)
	names.append(name)
	# summarize the performance along the way
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

运行该示例首先报告每个配置数量的决策树的平均准确性。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到在这个数据集上的表现有所提高，直到大约 100 棵树，之后保持不变。

>10 0.855 (0.037)
>50 0.876 (0.035)
>100 0.882 (0.037)
>500 0.885 (0.041)
>1000 0.885 (0.037)
>5000 0.885 (0.038)

为每个配置数量的树的准确度分数的分布创建一个方框和须图。

我们可以看到大约 100 棵树后没有进一步改善的总体趋势。

装袋集合大小与分类准确率的箱线图

探索样本数量

引导样本的大小也可以变化。

默认情况下，将创建一个与原始数据集具有相同数量示例的引导样本。使用较小的数据集可以增加生成的决策树的方差，并可能导致更好的整体表现。

用于拟合每个决策树的样本数量通过“ max_samples ”参数设置。

下面的示例将不同大小的样本作为原始数据集的 10%到 100%(默认值)的比率进行探索。

# explore bagging ensemble number of samples effect on performance
from numpy import mean
from numpy import std
from numpy import arange
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	# explore ratios from 10% to 100% in 10% increments
	for i in arange(0.1, 1.1, 0.1):
		key = '%.1f' % i
		models[key] = BaggingClassifier(max_samples=i)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
	# define the evaluation procedure
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model and collect the results
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	# evaluate the model
	scores = evaluate_model(model, X, y)
	# store the results
	results.append(scores)
	names.append(name)
	# summarize the performance along the way
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

运行该示例首先报告每个样本集大小的平均准确度。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，结果表明，随着样本大小的增加，表现通常会提高，这突出表明默认的 100%的训练数据集大小是合理的。

探索一个更小的样本量，并相应增加树的数量，以减少单个模型的方差，这可能也是有趣的。

>0.1 0.810 (0.036)
>0.2 0.836 (0.044)
>0.3 0.844 (0.043)
>0.4 0.843 (0.041)
>0.5 0.852 (0.034)
>0.6 0.855 (0.042)
>0.7 0.858 (0.042)
>0.8 0.861 (0.033)
>0.9 0.866 (0.041)
>1.0 0.864 (0.042)

为每个样本大小的准确度分数分布创建了一个方框和须图。

我们看到随着样本量的增加，准确性有增加的趋势。

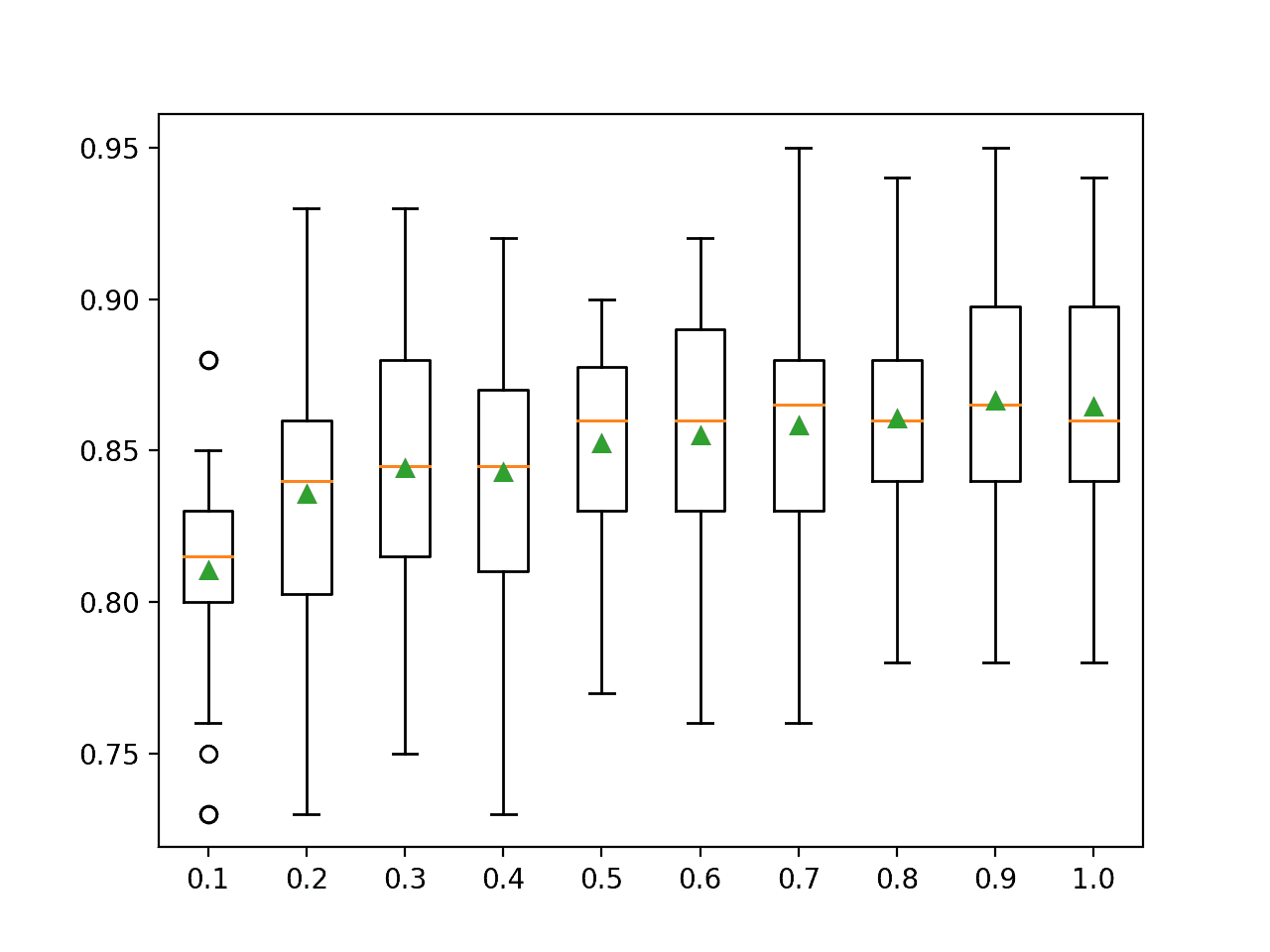
装袋样本量与分类准确度的箱线图

探索替代算法

决策树是装袋集成中最常用的算法。

这样做的原因是它们易于配置，具有较高的差异，并且通常表现良好。

其他算法可以与 bagging 一起使用，并且必须配置为具有适度高的方差。一个例子是 k 近邻算法，其中 k 值可以设置为低值。

集合中使用的算法是通过“ base_estimator ”参数指定的，并且必须设置为要使用的算法和算法配置的实例。

下面的例子演示了使用一个kneighgborcsclassifier作为装袋集成中使用的基本算法。这里，算法与默认超参数一起使用，其中 k 设置为 5。

# evaluate bagging with knn algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier(base_estimator=KNeighborsClassifier())
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到具有 KNN 和默认超参数的 Bagging 集成在这个测试数据集上实现了大约 88%的分类准确率。

Accuracy: 0.888 (0.036)

我们可以测试不同的 k 值，以找到模型方差的正确平衡，从而作为一个袋装集成获得良好的表现。

以下示例测试的袋装 KNN 模型的 k 值介于 1 和 20 之间。

# explore bagging ensemble k for knn effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
from sklearn.neighbors import KNeighborsClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	# evaluate k values from 1 to 20
	for i in range(1,21):
		# define the base model
		base = KNeighborsClassifier(n_neighbors=i)
		# define the ensemble model
		models[str(i)] = BaggingClassifier(base_estimator=base)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
	# define the evaluation procedure
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	# evaluate the model and collect the results
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1)
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	# evaluate the model
	scores = evaluate_model(model, X, y)
	# store the results
	results.append(scores)
	names.append(name)
	# summarize the performance along the way
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

运行该示例首先报告每个 k 值的平均准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，结果表明，当在 bagging 集合中使用时，较小的 k 值(例如 2 到 4)导致最佳的平均准确率。

>1 0.884 (0.025)
>2 0.890 (0.029)
>3 0.886 (0.035)
>4 0.887 (0.033)
>5 0.878 (0.037)
>6 0.879 (0.042)
>7 0.877 (0.037)
>8 0.877 (0.036)
>9 0.871 (0.034)
>10 0.877 (0.033)
>11 0.876 (0.037)
>12 0.877 (0.030)
>13 0.874 (0.034)
>14 0.871 (0.039)
>15 0.875 (0.034)
>16 0.877 (0.033)
>17 0.872 (0.034)
>18 0.873 (0.036)
>19 0.876 (0.034)
>20 0.876 (0.037)

为每个 k 值的准确度分数的分布创建一个方框和须图。

我们看到，在开始时，随着样本量的增加，准确度总体呈上升趋势，随后，随着集合中使用的单个 KNN 模型的方差随着更大的 k 值而增加，表现略有下降。

装袋 KNN 邻居数量与分类准确率的箱线图

装袋扩展

为了提高方法的表现，对 bagging 算法进行了许多修改和扩展。

也许最著名的是随机森林算法。

有一些不太出名但仍然有效的装袋扩展值得研究。

本节演示了其中的一些方法，例如粘贴集成、随机子空间集成和随机面片集成。

我们不是在数据集上与这些扩展赛跑，而是提供如何使用每种技术的工作示例，您可以复制粘贴这些技术，并尝试使用自己的数据集。

粘贴集成

粘贴集成是装袋的扩展，包括基于训练数据集的随机样本而不是自举样本来拟合集成成员。

该方法被设计成在训练数据集不适合存储的情况下使用比训练数据集更小的样本量。

该过程获取一小部分数据，在每一小部分数据上生成一个预测值，然后将这些预测值粘贴在一起。给出了一个可扩展到万亿字节数据集的版本。这些方法也适用于在线学习。

——在大型数据库和网上粘贴分类小票，1999。

下面的示例演示了粘贴集合，方法是将“ bootstrap ”参数设置为“ False ”，并将通过“ max_samples ”在训练数据集中使用的样本数量设置为适中的值，在本例中为训练数据集大小的 50%。

# evaluate pasting ensemble algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier(bootstrap=False, max_samples=0.5)
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到粘贴集成在这个数据集上实现了大约 84%的分类准确率。

Accuracy: 0.848 (0.039)

随机子空间集成

随机子空间集成是 bagging 的一个扩展，它涉及到基于从训练数据集中特征的随机子集构建的数据集来拟合集成成员。

它类似于随机森林，只是数据样本是随机的，而不是自举样本，并且为整个决策树选择特征子集，而不是在树中的每个分割点。

该分类器由通过伪随机选择特征向量的分量子集而系统地构建的多个树组成，即在随机选择的子空间中构建的树。

——构建决策森林的随机子空间方法，1998。

下面的示例演示了随机子空间集成，方法是将“ bootstrap ”参数设置为“ False ”，并将通过“ max_features ”在训练数据集中使用的特征数量设置为适中的值，在本例中为 10。

# evaluate random subspace ensemble algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier(bootstrap=False, max_features=10)
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到随机子空间集成在这个数据集上实现了大约 86%的分类准确率。

Accuracy: 0.862 (0.040)

我们期望在随机子空间中会有许多特征，提供模型方差和模型技能的正确平衡。

下面的例子演示了在从 1 到 20 的随机子空间集合中使用不同数量的特征的效果。

# explore random subspace ensemble ensemble number of features effect on performance
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
from matplotlib import pyplot

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
	return X, y

# get a list of models to evaluate
def get_models():
	models = dict()
	for i in range(1, 21):
		models[str(i)] = BaggingClassifier(bootstrap=False, max_features=i)
	return models

# evaluate a given model using cross-validation
def evaluate_model(model, X, y):
	cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
	scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
	return scores

# define dataset
X, y = get_dataset()
# get the models to evaluate
models = get_models()
# evaluate the models and store results
results, names = list(), list()
for name, model in models.items():
	scores = evaluate_model(model, X, y)
	results.append(scores)
	names.append(name)
	print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores)))
# plot model performance for comparison
pyplot.boxplot(results, labels=names, showmeans=True)
pyplot.show()

运行示例首先报告每个特征数量的平均准确率。

在这种情况下，结果表明使用数据集中大约一半数量的特征(例如，在 9 和 13 之间)可能给出该数据集上随机子空间集成的最佳结果。

>1 0.583 (0.047)
>2 0.659 (0.048)
>3 0.731 (0.038)
>4 0.775 (0.045)
>5 0.815 (0.044)
>6 0.820 (0.040)
>7 0.838 (0.034)
>8 0.841 (0.035)
>9 0.854 (0.036)
>10 0.854 (0.041)
>11 0.857 (0.034)
>12 0.863 (0.035)
>13 0.860 (0.043)
>14 0.856 (0.038)
>15 0.848 (0.043)
>16 0.847 (0.042)
>17 0.839 (0.046)
>18 0.831 (0.044)
>19 0.811 (0.043)
>20 0.802 (0.048)

为每个随机子空间大小的准确度分数的分布创建一个方框和须图。

我们看到了一个总体趋势，即随着特征数量的增加，准确率增加到大约 10 到 13 个特征，在这一水平上，准确率大致保持不变，然后表现呈适度下降趋势。

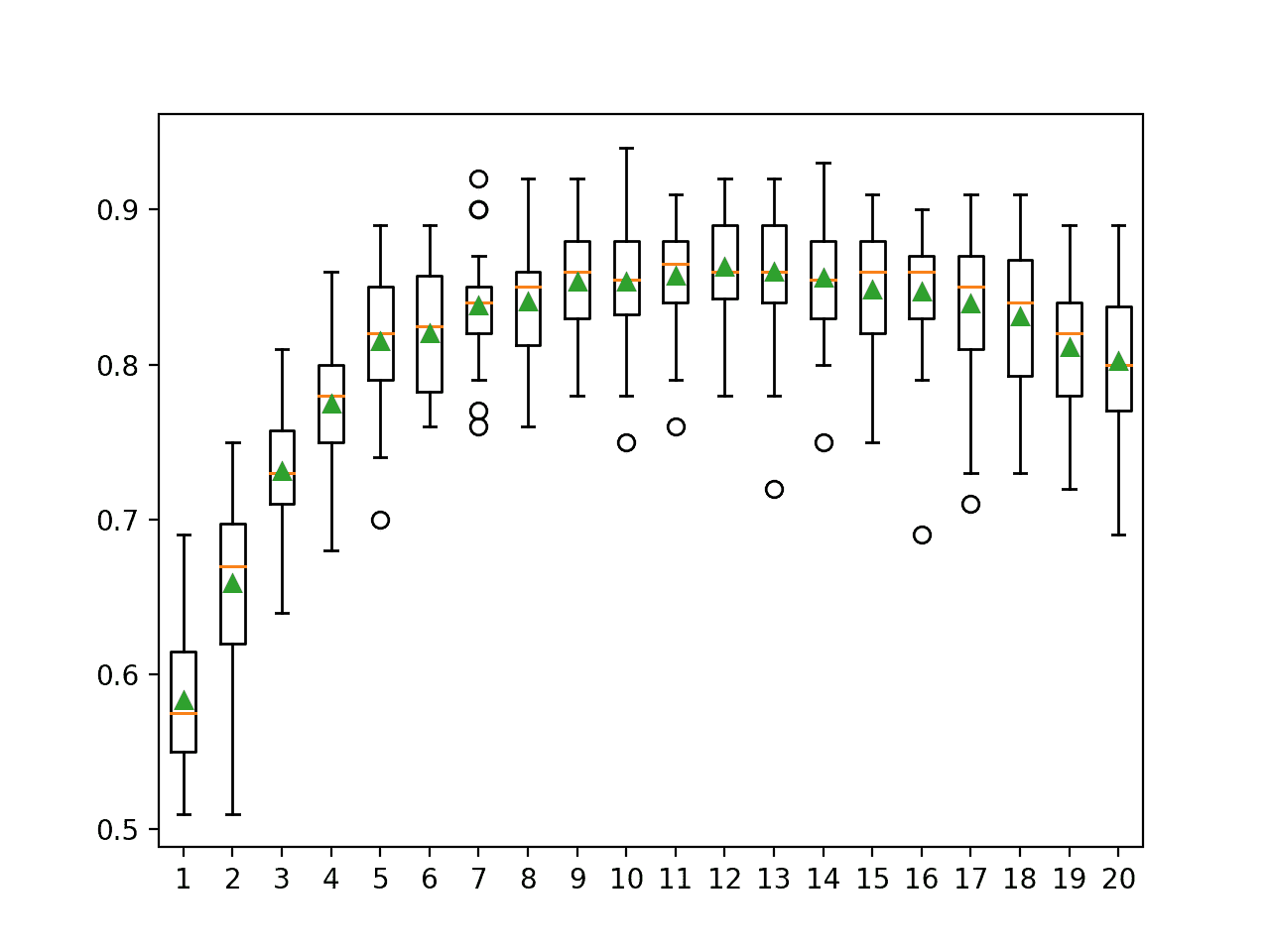
随机子空间集合特征数与分类准确率的箱线图

随机面片集合

随机面片集成是 bagging 的一个扩展，它包括基于由训练数据集的行(样本)和列(特征)的随机子集构建的数据集来拟合集成成员。

它不使用自举样本，并且可以被认为是组合了粘贴集合的数据集的随机采样和随机子空间集合的特征的随机采样的集合。

我们研究了一个非常简单但有效的集成框架，该框架通过从整个数据集中抽取实例和特征的随机子集，从随机数据块中构建集成的每个单独模型。

——随机补丁集成，2012 年。

下面的示例演示了随机面片集合，其中决策树是从训练数据集的随机样本创建的，样本大小限制为训练数据集的 50%，随机子集包含 10 个要素。

# evaluate random patches ensemble algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier(bootstrap=False, max_features=10, max_samples=0.5)
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

运行该示例会报告模型的均值和标准差准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到随机补丁集成在这个数据集上实现了大约 84%的分类准确率。

Accuracy: 0.845 (0.036)

常见问题

在这一节中，我们将更仔细地看看你在装袋集合过程中可能遇到的一些常见症结。

问:集成应该用什么算法？

该算法应该具有适度的方差，这意味着它适度地依赖于特定的训练数据。

决策树是默认使用的模型，因为它在实践中运行良好。可以使用其他算法，只要它们被配置为具有适度的方差。

选择的算法应该适度稳定，不像决策树桩那样不稳定，也不像修剪的决策树那样非常稳定，通常使用未修剪的决策树。

……众所周知，Bagging 应该用于不稳定的学习器，一般来说，越不稳定，表现提升越大。

—第 52 页，集合方法，2012。

问:应该用多少个文工团成员？

模型的表现将随着决策树数量的增加而收敛到一个点，然后保持水平。

Bagging 的表现随着集成规模(即基础学习器的数量)的增长而收敛…

—第 52 页，集合方法，2012。

因此，不断增加树的数量，直到数据集的表现稳定下来。

问:文工团不会因为树木太多而过度吗？

不。装袋集成一般来说不太可能过量。

问:自举样本应该有多大？

让引导样本与原始数据集大小一样大是一种好的做法。

这是原始数据集的 100%大小或相等的行数。

问:哪些问题很适合装袋？

一般来说，装袋非常适合小规模或中等规模数据集的问题。但这是一个粗略的指南。

Bagging 最适合于可用训练数据集相对较小的问题。

—第 12 页，集成机器学习，2012。

试试看吧。

进一步阅读

如果您想更深入地了解这个主题，本节将提供更多资源。

教程

• 引导法的简单介绍
• 如何用 Python 实现从零开始装袋
• 如何在 Keras 创建深度学习模型的装袋集成
• 机器学习的装袋和随机森林集成算法

报纸

• 装袋预测因子，1996。
• 在大型数据库和网上粘贴分类小票，1999。
• 构建决策森林的随机子空间方法，1998。
• 随机面片集合，2012。

蜜蜂

• 硬化。一起。bagginclassifier API。
• 硬化。一起。bagginger return API。

文章

• 引导聚合，维基百科。

摘要

在本教程中，您发现了如何开发用于分类和回归的 Bagging 集成。

具体来说，您了解到:

• Bagging 集成是从适合数据集不同样本的决策树创建的集成。
• 如何用 Sklearn 使用 Bagging 集成进行分类和回归。
• 如何探索 Bagging 模型超参数对模型表现的影响。

你有什么问题吗？
在下面的评论中提问，我会尽力回答。

使用 Python 的混合集成机器学习

原文：https://machinelearningmastery.com/blending-ensemble-machine-learning-with-python/

最后更新于 2021 年 4 月 27 日

融合是一种集成机器学习算法。

这是一个口语化的名称堆叠泛化或堆叠集成，其中不是将元模型拟合到基础模型做出的折外预测上，而是将其拟合到保持数据集上做出的预测上。

混合被用来描述堆叠模型，在 100 万美元的网飞机器学习竞赛中，竞争对手将数百个预测模型组合在一起，因此，在竞争激烈的机器学习圈子(如 Kaggle 社区)中，混合仍然是一种流行的堆叠技术和名称。

在本教程中，您将发现如何在 python 中开发和评估混合集成。

完成本教程后，您将知道:

• 混合集成是一种堆叠类型，其中元模型使用保持验证数据集上的预测来拟合，而不是折叠预测。
• 如何开发混合集成，包括用于训练模型和对新数据进行预测的功能。
• 如何评估分类和回归预测建模问题的混合集成？

用我的新书Python 集成学习算法启动你的项目，包括分步教程和所有示例的 Python 源代码文件。

我们开始吧。

将集成机器学习与 Python 融合
图片由 Nathalie 提供，保留部分权利。

教程概述

本教程分为四个部分；它们是:

1. 混合集成
2. 开发混合集成
3. 用于分类的混合集成
4. 回归的混合集成

混合集成

混合是一种集成机器学习技术，它使用机器学习模型来学习如何最好地组合来自多个贡献集成成员模型的预测。

因此，混合与堆叠概括相同，称为堆叠，广义上来说。通常，在同一篇论文或模型描述中，混合和堆叠可以互换使用。

许多机器学习实践者已经成功地使用堆叠和相关技术来提高预测准确率，使其超过任何单个模型获得的水平。在某些情况下，堆叠也被称为混合，我们将在这里互换使用这些术语。

——特征加权线性叠加，2009。

堆叠模型的体系结构包括两个或多个基础模型，通常称为 0 级模型，以及一个组合基础模型预测的元模型，称为 1 级模型。元模型基于基础模型对样本外数据的预测进行训练。

• 0 级模型 ( 基础模型):模型适合训练数据，并且其预测被编译。
• 一级模型 ( 元模型):学习如何最好地组合基础模型预测的模型。

然而，混合对于如何构建堆叠集成模型有特定的含义。

混合可能建议开发一个堆叠集成，其中基础模型是任何类型的机器学习模型，元模型是一个线性模型，它将基础模型的预测“混合”。

*例如，当预测数值时的线性回归模型或当预测类别标签时的逻辑回归模型将计算由基础模型做出的预测的加权和，并将被认为是预测的混合。

• 混合集成:使用线性模型，如线性回归或逻辑回归，作为堆叠集成中的元模型。

2009 年网飞奖期间，混合是堆叠集成常用的术语。该奖项涉及寻求比原生网飞算法表现更好的电影推荐预测的团队，获得 100 万美元奖金的团队获得了 10%的业绩提升。

我们的 RMSE=0.8643² 解决方案是 100 多个结果的线性混合。[……]在整个方法描述中，我们强调了参与最终混合解决方案的具体预测因素。

——BellKor 2008 年 Netflix 大奖解决方案，2008 年。

因此，混合是一个口语术语，指的是具有堆叠型架构模型的集成学习。除了与竞争性机器学习相关的内容之外，它很少被用于教科书或学术论文。

最常见的是，混合用于描述堆叠的具体应用，其中元模型是基于基础模型在搁置验证数据集上做出的预测来训练的。在这种情况下，堆叠是为元模型保留的，元模型是在交叉验证过程中对折外预测进行训练的。

• 混合:堆叠式集成，其中元模型基于在保持数据集上做出的预测进行训练。
• 叠加:叠加型集合，其中元模型基于 k 倍交叉验证期间做出的超折叠预测进行训练。

这种区别在 Kaggle 竞争机器学习社区中很常见。

混合是网飞获奖者引入的一个词。它非常接近于堆叠概括，但更简单一点，信息泄露的风险也更小。[……]通过混合，而不是为列车组创建不一致的预测，您创建了一个小的保持组，比如说 10%的列车组。然后，堆垛机模型仅在该保持装置上运行。

——kag gle 联合指南，MLWave，2015 年。

我们将使用混合的后一种定义。

接下来，让我们看看如何实现混合。

开发混合集成

Sklearn 库在编写本文时并不支持混合。

相反，我们可以使用 Sklearn 模型自己实现它。

首先，我们需要创建一些基础模型。对于回归或分类问题，这些可以是我们喜欢的任何模型。我们可以定义一个函数 get_models() ，该函数返回一个模型列表，其中每个模型被定义为一个元组，该元组有一个名称和配置的分类器或回归对象。

例如，对于分类问题，我们可以使用逻辑回归、知识网络、决策树、SVM 和朴素贝叶斯模型。

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LogisticRegression()))
	models.append(('knn', KNeighborsClassifier()))
	models.append(('cart', DecisionTreeClassifier()))
	models.append(('svm', SVC(probability=True)))
	models.append(('bayes', GaussianNB()))
	return models

接下来，我们需要拟合混合模型。

回想一下，基础模型适合训练数据集。元模型适合于保持数据集上每个基础模型所做的预测。

首先，我们可以枚举模型列表，并在训练数据集上依次拟合每个模型。同样在这个循环中，我们可以使用拟合模型对保持(验证)数据集进行预测，并存储预测供以后使用。

...
# fit all models on the training set and predict on hold out set
meta_X = list()
for name, model in models:
	# fit in training set
	model.fit(X_train, y_train)
	# predict on hold out set
	yhat = model.predict(X_val)
	# reshape predictions into a matrix with one column
	yhat = yhat.reshape(len(yhat), 1)
	# store predictions as input for blending
	meta_X.append(yhat)

我们现在有了“ meta_X ”，它代表了可以用来训练元模型的输入数据。每个列或特征代表一个基本模型的输出。

每行代表保持数据集中的一个样本。我们可以使用 hstack()函数来确保该数据集是机器学习模型所期望的 2D numpy 数组。

...
# create 2d array from predictions, each set is an input feature
meta_X = hstack(meta_X)

我们现在可以训练我们的元模型了。这可以是我们喜欢的任何机器学习模型，例如用于分类的逻辑回归。

...
# define blending model
blender = LogisticRegression()
# fit on predictions from base models
blender.fit(meta_X, y_val)

我们可以将所有这些结合到一个名为 fit_ensemble() 的函数中，该函数使用训练数据集和保持验证数据集来训练混合模型。

# fit the blending ensemble
def fit_ensemble(models, X_train, X_val, y_train, y_val):
	# fit all models on the training set and predict on hold out set
	meta_X = list()
	for name, model in models:
		# fit in training set
		model.fit(X_train, y_train)
		# predict on hold out set
		yhat = model.predict(X_val)
		# reshape predictions into a matrix with one column
		yhat = yhat.reshape(len(yhat), 1)
		# store predictions as input for blending
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# define blending model
	blender = LogisticRegression()
	# fit on predictions from base models
	blender.fit(meta_X, y_val)
	return blender

下一步是使用混合集成对新数据进行预测。

这是一个分两步走的过程。第一步是使用每个基本模型进行预测。然后，这些预测被收集在一起，并用作混合模型的输入，以做出最终预测。

我们可以使用与训练模型时相同的循环结构。也就是说，我们可以将每个基础模型的预测收集到一个训练数据集中，将预测堆叠在一起，并使用这个元级数据集在 blender 模型上调用 predict() 。

下面的 predict_ensemble() 函数实现了这一点。给定拟合基础模型、拟合混合器集合和数据集(如测试数据集或新数据)的列表，它将返回数据集的一组预测。

# make a prediction with the blending ensemble
def predict_ensemble(models, blender, X_test):
	# make predictions with base models
	meta_X = list()
	for name, model in models:
		# predict with base model
		yhat = model.predict(X_test)
		# reshape predictions into a matrix with one column
		yhat = yhat.reshape(len(yhat), 1)
		# store prediction
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# predict
	return blender.predict(meta_X)

我们现在已经拥有了为分类或回归预测建模问题实现混合集成所需的所有元素

用于分类的混合集成

在这一节中，我们将研究混合在分类问题中的应用。

首先，我们可以使用 make_classification()函数创建一个包含 10，000 个示例和 20 个输入特征的合成二进制分类问题。

下面列出了完整的示例。

# test classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
# summarize the dataset
print(X.shape, y.shape)

运行该示例将创建数据集并总结输入和输出组件的形状。

(10000, 20) (10000,)

接下来，我们需要将数据集分成训练集和测试集，然后将训练集分成用于训练基本模型的子集和用于训练元模型的子集。

在这种情况下，我们将对训练集和测试集使用 50-50 的分割，然后对训练集和验证集使用 67-33 的分割。

...
# split dataset into train and test sets
X_train_full, X_test, y_train_full, y_test = train_test_split(X, y, test_size=0.5, random_state=1)
# split training set into train and validation sets
X_train, X_val, y_train, y_val = train_test_split(X_train_full, y_train_full, test_size=0.33, random_state=1)
# summarize data split
print('Train: %s, Val: %s, Test: %s' % (X_train.shape, X_val.shape, X_test.shape))

然后，我们可以使用上一节中的 get_models() 函数来创建集成中使用的分类模型。

然后可以调用*拟合集合()函数来拟合训练和验证数据集上的混合集合，并且可以使用预测集合()*函数来对保持数据集进行预测。

...
# create the base models
models = get_models()
# train the blending ensemble
blender = fit_ensemble(models, X_train, X_val, y_train, y_val)
# make predictions on test set
yhat = predict_ensemble(models, blender, X_test)

最后，我们可以通过在测试数据集上报告分类准确率来评估混合模型的表现。

...
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Blending Accuracy: %.3f' % score)

将所有这些联系在一起，下面列出了在合成二分类问题上评估混合集成的完整示例。

# blending ensemble for classification using hard voting
from numpy import hstack
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
	return X, y

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LogisticRegression()))
	models.append(('knn', KNeighborsClassifier()))
	models.append(('cart', DecisionTreeClassifier()))
	models.append(('svm', SVC()))
	models.append(('bayes', GaussianNB()))
	return models

# fit the blending ensemble
def fit_ensemble(models, X_train, X_val, y_train, y_val):
	# fit all models on the training set and predict on hold out set
	meta_X = list()
	for name, model in models:
		# fit in training set
		model.fit(X_train, y_train)
		# predict on hold out set
		yhat = model.predict(X_val)
		# reshape predictions into a matrix with one column
		yhat = yhat.reshape(len(yhat), 1)
		# store predictions as input for blending
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# define blending model
	blender = LogisticRegression()
	# fit on predictions from base models
	blender.fit(meta_X, y_val)
	return blender

# make a prediction with the blending ensemble
def predict_ensemble(models, blender, X_test):
	# make predictions with base models
	meta_X = list()
	for name, model in models:
		# predict with base model
		yhat = model.predict(X_test)
		# reshape predictions into a matrix with one column
		yhat = yhat.reshape(len(yhat), 1)
		# store prediction
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# predict
	return blender.predict(meta_X)

# define dataset
X, y = get_dataset()
# split dataset into train and test sets
X_train_full, X_test, y_train_full, y_test = train_test_split(X, y, test_size=0.5, random_state=1)
# split training set into train and validation sets
X_train, X_val, y_train, y_val = train_test_split(X_train_full, y_train_full, test_size=0.33, random_state=1)
# summarize data split
print('Train: %s, Val: %s, Test: %s' % (X_train.shape, X_val.shape, X_test.shape))
# create the base models
models = get_models()
# train the blending ensemble
blender = fit_ensemble(models, X_train, X_val, y_train, y_val)
# make predictions on test set
yhat = predict_ensemble(models, blender, X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Blending Accuracy: %.3f' % (score*100))

运行该示例首先报告训练、验证和测试数据集的形状，然后报告测试数据集上集成的准确性。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到混合集成实现了大约 97.900%的分类准确率。

Train: (3350, 20), Val: (1650, 20), Test: (5000, 20)
Blending Accuracy: 97.900

在前面的示例中，使用混合模型组合了清晰的类标签预测。这是一种硬投票的类型。

另一种方法是让每个模型预测类概率，并使用元模型来混合概率。这是一种软投票，在某些情况下可以产生更好的表现。

首先，我们必须将模型配置为返回概率，例如 SVM 模型。

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LogisticRegression()))
	models.append(('knn', KNeighborsClassifier()))
	models.append(('cart', DecisionTreeClassifier()))
	models.append(('svm', SVC(probability=True)))
	models.append(('bayes', GaussianNB()))
	return models

接下来，我们必须改变基本模型来预测概率，而不是简单的类标签。

这可以通过在拟合基础模型时调用拟合 _ 集合()函数中的预测 _proba() 函数来实现。

...
# fit all models on the training set and predict on hold out set
meta_X = list()
for name, model in models:
	# fit in training set
	model.fit(X_train, y_train)
	# predict on hold out set
	yhat = model.predict_proba(X_val)
	# store predictions as input for blending
	meta_X.append(yhat)

这意味着用于训练元模型的元数据集每个分类器将有 n 列，其中 n 是预测问题中的类的数量，在我们的例子中是两个。

当使用混合模型对新数据进行预测时，我们还需要更改基础模型所做的预测。

...
# make predictions with base models
meta_X = list()
for name, model in models:
	# predict with base model
	yhat = model.predict_proba(X_test)
	# store prediction
	meta_X.append(yhat)

将这些联系在一起，下面列出了对合成二进制分类问题的预测类概率使用混合的完整示例。

# blending ensemble for classification using soft voting
from numpy import hstack
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
	return X, y

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LogisticRegression()))
	models.append(('knn', KNeighborsClassifier()))
	models.append(('cart', DecisionTreeClassifier()))
	models.append(('svm', SVC(probability=True)))
	models.append(('bayes', GaussianNB()))
	return models

# fit the blending ensemble
def fit_ensemble(models, X_train, X_val, y_train, y_val):
	# fit all models on the training set and predict on hold out set
	meta_X = list()
	for name, model in models:
		# fit in training set
		model.fit(X_train, y_train)
		# predict on hold out set
		yhat = model.predict_proba(X_val)
		# store predictions as input for blending
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# define blending model
	blender = LogisticRegression()
	# fit on predictions from base models
	blender.fit(meta_X, y_val)
	return blender

# make a prediction with the blending ensemble
def predict_ensemble(models, blender, X_test):
	# make predictions with base models
	meta_X = list()
	for name, model in models:
		# predict with base model
		yhat = model.predict_proba(X_test)
		# store prediction
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# predict
	return blender.predict(meta_X)

# define dataset
X, y = get_dataset()
# split dataset into train and test sets
X_train_full, X_test, y_train_full, y_test = train_test_split(X, y, test_size=0.5, random_state=1)
# split training set into train and validation sets
X_train, X_val, y_train, y_val = train_test_split(X_train_full, y_train_full, test_size=0.33, random_state=1)
# summarize data split
print('Train: %s, Val: %s, Test: %s' % (X_train.shape, X_val.shape, X_test.shape))
# create the base models
models = get_models()
# train the blending ensemble
blender = fit_ensemble(models, X_train, X_val, y_train, y_val)
# make predictions on test set
yhat = predict_ensemble(models, blender, X_test)
# evaluate predictions
score = accuracy_score(y_test, yhat)
print('Blending Accuracy: %.3f' % (score*100))

运行该示例首先报告训练、验证和测试数据集的形状，然后报告测试数据集上集成的准确性。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到混合类概率导致分类准确率提升到大约 98.240%。

Train: (3350, 20), Val: (1650, 20), Test: (5000, 20)
Blending Accuracy: 98.240

混合集成只有在能够超越任何单个贡献模型时才有效。

我们可以通过单独评估每个基础模型来证实这一点。每个基础模型可以适合整个训练数据集(不同于混合集成)，并在测试数据集上进行评估(就像混合集成一样)。

下面的示例演示了这一点，单独评估每个基础模型。

# evaluate base models on the entire training dataset
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
	return X, y

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LogisticRegression()))
	models.append(('knn', KNeighborsClassifier()))
	models.append(('cart', DecisionTreeClassifier()))
	models.append(('svm', SVC(probability=True)))
	models.append(('bayes', GaussianNB()))
	return models

# define dataset
X, y = get_dataset()
# split dataset into train and test sets
X_train_full, X_test, y_train_full, y_test = train_test_split(X, y, test_size=0.5, random_state=1)
# summarize data split
print('Train: %s, Test: %s' % (X_train_full.shape, X_test.shape))
# create the base models
models = get_models()
# evaluate standalone model
for name, model in models:
	# fit the model on the training dataset
	model.fit(X_train_full, y_train_full)
	# make a prediction on the test dataset
	yhat = model.predict(X_test)
	# evaluate the predictions
	score = accuracy_score(y_test, yhat)
	# report the score
	print('>%s Accuracy: %.3f' % (name, score*100))

运行该示例首先报告完整训练和测试数据集的形状，然后报告测试数据集上每个基础模型的准确率。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到所有模型的表现都比混合集成差。

有趣的是，我们可以看到 SVM 非常接近达到 98.200%的准确率，相比之下混合集成达到 98.240%。

Train: (5000, 20), Test: (5000, 20)
>lr Accuracy: 87.800
>knn Accuracy: 97.380
>cart Accuracy: 88.200
>svm Accuracy: 98.200
>bayes Accuracy: 87.300

我们可以选择使用混合集成作为我们的最终模型。

这包括在整个训练数据集上拟合集合，并对新的例子进行预测。具体来说，将整个训练数据集分割成训练集和验证集，分别训练基本模型和元模型，然后可以使用集成进行预测。

下面列出了使用混合集成对新数据进行分类预测的完整示例。

# example of making a prediction with a blending ensemble for classification
from numpy import hstack
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB

# get the dataset
def get_dataset():
	X, y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=7)
	return X, y

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LogisticRegression()))
	models.append(('knn', KNeighborsClassifier()))
	models.append(('cart', DecisionTreeClassifier()))
	models.append(('svm', SVC(probability=True)))
	models.append(('bayes', GaussianNB()))
	return models

# fit the blending ensemble
def fit_ensemble(models, X_train, X_val, y_train, y_val):
	# fit all models on the training set and predict on hold out set
	meta_X = list()
	for _, model in models:
		# fit in training set
		model.fit(X_train, y_train)
		# predict on hold out set
		yhat = model.predict_proba(X_val)
		# store predictions as input for blending
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# define blending model
	blender = LogisticRegression()
	# fit on predictions from base models
	blender.fit(meta_X, y_val)
	return blender

# make a prediction with the blending ensemble
def predict_ensemble(models, blender, X_test):
	# make predictions with base models
	meta_X = list()
	for _, model in models:
		# predict with base model
		yhat = model.predict_proba(X_test)
		# store prediction
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# predict
	return blender.predict(meta_X)

# define dataset
X, y = get_dataset()
# split dataset set into train and validation sets
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.33, random_state=1)
# summarize data split
print('Train: %s, Val: %s' % (X_train.shape, X_val.shape))
# create the base models
models = get_models()
# train the blending ensemble
blender = fit_ensemble(models, X_train, X_val, y_train, y_val)
# make a prediction on a new row of data
row = [-0.30335011, 2.68066314, 2.07794281, 1.15253537, -2.0583897, -2.51936601, 0.67513028, -3.20651939, -1.60345385, 3.68820714, 0.05370913, 1.35804433, 0.42011397, 1.4732839, 2.89997622, 1.61119399, 7.72630965, -2.84089477, -1.83977415, 1.34381989]
yhat = predict_ensemble(models, blender, [row])
# summarize prediction
print('Predicted Class: %d' % (yhat))

运行该示例适合数据集上的混合集成模型，然后用于对新的数据行进行预测，就像我们在应用程序中使用该模型时可能做的那样。

Train: (6700, 20), Val: (3300, 20)
Predicted Class: 1

接下来，让我们探索如何评估回归的混合集合。

回归的混合集成

在这一节中，我们将研究使用堆叠来解决回归问题。

首先，我们可以使用make _ revolution()函数创建一个包含 10，000 个示例和 20 个输入特征的合成回归问题。

下面列出了完整的示例。

# test regression dataset
from sklearn.datasets import make_regression
# define dataset
X, y = make_regression(n_samples=10000, n_features=20, n_informative=10, noise=0.3, random_state=7)
# summarize the dataset
print(X.shape, y.shape)

运行该示例将创建数据集并总结输入和输出组件的形状。

(10000, 20) (10000,)

接下来，我们可以定义用作基础模型的回归模型列表。在这种情况下，我们将使用线性回归、kNN、决策树和 SVM 模型。

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LinearRegression()))
	models.append(('knn', KNeighborsRegressor()))
	models.append(('cart', DecisionTreeRegressor()))
	models.append(('svm', SVR()))
	return models

用于训练混合集成的 fit_ensemble() 函数与分类没有变化，除了用于混合的模型必须改为回归模型。

在这种情况下，我们将使用线性回归模型。

...
# define blending model
blender = LinearRegression()

假设这是一个回归问题，我们将使用误差度量来评估模型的表现，在这种情况下，是平均绝对误差，简称 MAE。

...
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('Blending MAE: %.3f' % score)

将这些联系在一起，下面列出了合成回归预测建模问题的混合集成的完整示例。

# evaluate blending ensemble for regression
from numpy import hstack
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import SVR

# get the dataset
def get_dataset():
	X, y = make_regression(n_samples=10000, n_features=20, n_informative=10, noise=0.3, random_state=7)
	return X, y

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LinearRegression()))
	models.append(('knn', KNeighborsRegressor()))
	models.append(('cart', DecisionTreeRegressor()))
	models.append(('svm', SVR()))
	return models

# fit the blending ensemble
def fit_ensemble(models, X_train, X_val, y_train, y_val):
	# fit all models on the training set and predict on hold out set
	meta_X = list()
	for name, model in models:
		# fit in training set
		model.fit(X_train, y_train)
		# predict on hold out set
		yhat = model.predict(X_val)
		# reshape predictions into a matrix with one column
		yhat = yhat.reshape(len(yhat), 1)
		# store predictions as input for blending
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# define blending model
	blender = LinearRegression()
	# fit on predictions from base models
	blender.fit(meta_X, y_val)
	return blender

# make a prediction with the blending ensemble
def predict_ensemble(models, blender, X_test):
	# make predictions with base models
	meta_X = list()
	for name, model in models:
		# predict with base model
		yhat = model.predict(X_test)
		# reshape predictions into a matrix with one column
		yhat = yhat.reshape(len(yhat), 1)
		# store prediction
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# predict
	return blender.predict(meta_X)

# define dataset
X, y = get_dataset()
# split dataset into train and test sets
X_train_full, X_test, y_train_full, y_test = train_test_split(X, y, test_size=0.5, random_state=1)
# split training set into train and validation sets
X_train, X_val, y_train, y_val = train_test_split(X_train_full, y_train_full, test_size=0.33, random_state=1)
# summarize data split
print('Train: %s, Val: %s, Test: %s' % (X_train.shape, X_val.shape, X_test.shape))
# create the base models
models = get_models()
# train the blending ensemble
blender = fit_ensemble(models, X_train, X_val, y_train, y_val)
# make predictions on test set
yhat = predict_ensemble(models, blender, X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('Blending MAE: %.3f' % score)

运行该示例首先报告训练、验证和测试数据集的形状，然后报告测试数据集上集合的 MAE。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到混合集成在测试数据集上实现了大约 0.237 的 MAE。

Train: (3350, 20), Val: (1650, 20), Test: (5000, 20)
Blending MAE: 0.237

与分类一样，混合集成只有在表现优于任何有助于集成的基础模型时才是有用的。

我们可以通过单独评估每个基础模型来检查这一点，方法是首先在整个训练数据集上拟合它(不同于混合集成)，然后在测试数据集上进行预测(类似于混合集成)。

下面的示例在合成回归预测建模数据集上单独评估每个基本模型。

# evaluate base models in isolation on the regression dataset
from numpy import hstack
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import SVR

# get the dataset
def get_dataset():
	X, y = make_regression(n_samples=10000, n_features=20, n_informative=10, noise=0.3, random_state=7)
	return X, y

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LinearRegression()))
	models.append(('knn', KNeighborsRegressor()))
	models.append(('cart', DecisionTreeRegressor()))
	models.append(('svm', SVR()))
	return models

# define dataset
X, y = get_dataset()
# split dataset into train and test sets
X_train_full, X_test, y_train_full, y_test = train_test_split(X, y, test_size=0.5, random_state=1)
# summarize data split
print('Train: %s, Test: %s' % (X_train_full.shape, X_test.shape))
# create the base models
models = get_models()
# evaluate standalone model
for name, model in models:
	# fit the model on the training dataset
	model.fit(X_train_full, y_train_full)
	# make a prediction on the test dataset
	yhat = model.predict(X_test)
	# evaluate the predictions
	score = mean_absolute_error(y_test, yhat)
	# report the score
	print('>%s MAE: %.3f' % (name, score))

运行该示例首先报告完整的训练和测试数据集的形状，然后报告测试数据集上每个基础模型的 MAE。

注:考虑到算法或评估程序的随机性，或数值准确率的差异，您的结果可能会有所不同。考虑运行该示例几次，并比较平均结果。

在这种情况下，我们可以看到线性回归模型确实比混合集成表现得稍好，实现了 0.236 的 MAE，而集成为 0.237。这可能是因为合成数据集的构建方式。

然而，在这种情况下，我们会选择使用线性回归模型直接解决这个问题。这突出了在采用集合模型作为最终模型之前检查贡献模型的表现的重要性。

Train: (5000, 20), Test: (5000, 20)
>lr MAE: 0.236
>knn MAE: 100.169
>cart MAE: 133.744
>svm MAE: 138.195

同样，我们可以选择使用混合集合作为回归的最终模型。

这包括拟合将整个数据集分割成训练集和验证集，以分别拟合基本模型和元模型，然后集成可以用于预测新的数据行。

下面列出了使用混合集合对新数据进行回归预测的完整示例。

# example of making a prediction with a blending ensemble for regression
from numpy import hstack
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import SVR

# get the dataset
def get_dataset():
	X, y = make_regression(n_samples=10000, n_features=20, n_informative=10, noise=0.3, random_state=7)
	return X, y

# get a list of base models
def get_models():
	models = list()
	models.append(('lr', LinearRegression()))
	models.append(('knn', KNeighborsRegressor()))
	models.append(('cart', DecisionTreeRegressor()))
	models.append(('svm', SVR()))
	return models

# fit the blending ensemble
def fit_ensemble(models, X_train, X_val, y_train, y_val):
	# fit all models on the training set and predict on hold out set
	meta_X = list()
	for _, model in models:
		# fit in training set
		model.fit(X_train, y_train)
		# predict on hold out set
		yhat = model.predict(X_val)
		# reshape predictions into a matrix with one column
		yhat = yhat.reshape(len(yhat), 1)
		# store predictions as input for blending
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# define blending model
	blender = LinearRegression()
	# fit on predictions from base models
	blender.fit(meta_X, y_val)
	return blender

# make a prediction with the blending ensemble
def predict_ensemble(models, blender, X_test):
	# make predictions with base models
	meta_X = list()
	for _, model in models:
		# predict with base model
		yhat = model.predict(X_test)
		# reshape predictions into a matrix with one column
		yhat = yhat.reshape(len(yhat), 1)
		# store prediction
		meta_X.append(yhat)
	# create 2d array from predictions, each set is an input feature
	meta_X = hstack(meta_X)
	# predict
	return blender.predict(meta_X)

# define dataset
X, y = get_dataset()
# split dataset set into train and validation sets
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.33, random_state=1)
# summarize data split
print('Train: %s, Val: %s' % (X_train.shape, X_val.shape))
# create the base models
models = get_models()
# train the blending ensemble
blender = fit_ensemble(models, X_train, X_val, y_train, y_val)
# make a prediction on a new row of data
row = [-0.24038754, 0.55423865, -0.48979221, 1.56074459, -1.16007611, 1.10049103, 1.18385406, -1.57344162, 0.97862519, -0.03166643, 1.77099821, 1.98645499, 0.86780193, 2.01534177, 2.51509494, -1.04609004, -0.19428148, -0.05967386, -2.67168985, 1.07182911]
yhat = predict_ensemble(models, blender, [row])
# summarize prediction
print('Predicted: %.3f' % (yhat[0]))

运行该示例适合数据集上的混合集成模型，然后用于对新的数据行进行预测，就像我们在应用程序中使用该模型时可能做的那样。

Train: (6700, 20), Val: (3300, 20)
Predicted: 359.986

进一步阅读

如果您想更深入地了解这个主题，本节将提供更多资源。

相关教程

• 用 Python 堆叠集成机器学习
• 如何用 Python 从零开始实现堆叠泛化(堆叠)

报纸

• 特征加权线性叠加，2009。
• BellKor 2008 年 Netflix 奖的解决方案，2008 年。
• 鹿儿岛联合指南，mlwave2015 年。

文章

• 网飞奖，维基百科。

摘要

在本教程中，您发现了如何在 python 中开发和评估混合集成。

具体来说，您了解到:

• 混合集成是一种堆叠类型，其中元模型使用保持验证数据集上的预测来拟合，而不是折叠预测。
• 如何开发混合集成，包括用于训练模型和对新数据进行预测的功能。
• 如何评估分类和回归预测建模问题的混合集成？

你有什么问题吗？
在下面的评论中提问，我会尽力回答。*