Scikit-Learn 1.4使用指南：集成学习：梯度提升、随机森林、装袋、投票、堆叠

集成学习：梯度提升、随机森林、装袋、投票、堆叠

sklearn.ensemble

集成学习方法将使用给定学习算法构建的多个基本估计器的预测结果结合起来，以提高单个估计器的泛化能力和鲁棒性。

两个非常著名的集成学习方法的例子是梯度提升树<gradient_boosting>和随机森林<forest>。

更一般地说，集成模型可以应用于除了树之外的任何基本学习器，例如平均方法中的装袋方法<bagging>、模型堆叠<stacking>或投票<voting_classifier>，或者在提升中，例如AdaBoost<adaboost>。

梯度提升树

梯度提升树或梯度提升决策树（GBDT）是将提升方法推广到任意可微分损失函数的方法，详见【Friedman2001】的开创性工作。GBDT是一种非常优秀的回归和分类模型，特别适用于表格数据。

GradientBoostingClassifier与HistGradientBoostingClassifier的比较

Scikit-learn提供了两种梯度提升树的实现：用于分类的HistGradientBoostingClassifier和GradientBoostingClassifier，以及用于回归的相应类。当样本数量大于数万个时，前者可以比后者快数个数量级。

Hist...版本原生支持缺失值和分类数据，无需进行额外的预处理，如插补。

对于样本量较小的情况，可能更倾向于使用GradientBoostingClassifier和GradientBoostingRegressor，因为在这种情况下，分箱可能会导致分割点过于近似。

基于直方图的梯度提升

Scikit-learn 0.21引入了两种基于直方图的梯度提升树实现，即HistGradientBoostingClassifier和HistGradientBoostingRegressor，灵感来自LightGBM（参见【LightGBM】）。

当样本数量大于数万个时，这些基于直方图的估计器可以比GradientBoostingClassifier和GradientBoostingRegressor快数个数量级。

它们还原生支持缺失值，无需插补。

这些快速估计器首先将输入样本X分成整数值的箱（通常为256个箱），这极大地减少了需要考虑的分割点数量，并且在构建树时可以利用基于整数的数据结构（直方图），而不是依赖于排序的连续值。这些估计器的API略有不同，并且尚不支持GradientBoostingClassifier和GradientBoostingRegressor的某些特性，例如某些损失函数。

示例：

• sphx_glr_auto_examples_inspection_plot_partial_dependence.py

用法

大多数参数与GradientBoostingClassifier和GradientBoostingRegressor相同。唯一的例外是max_iter参数，它替代了n_estimators，并控制提升过程的迭代次数：

>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> from sklearn.datasets import make_hastie_10_2

>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]

>>> clf = HistGradientBoostingClassifier(max_iter=100).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.8965

回归问题可用的损失函数有“平方误差”和“绝对误差”（对异常值不敏感），以及适用于计数和频率建模的“泊松”损失函数。对于分类问题，只有“对数损失”可用。对于二分类问题，它使用二元对数损失，也称为二项偏差或二元交叉熵。对于n_classes >= 3，它使用多类别对数损失函数，其中多项偏差和分类交叉熵是替代名称。根据传递给fit的y，选择适当的损失版本。

树的大小可以通过max_leaf_nodes、max_depth和min_samples_leaf参数进行控制。

用于对数据进行分箱的箱数由max_bins参数控制。使用更少的箱数相当于一种正则化形式。通常建议使用尽可能多的箱数（256），这是默认值。

l2_regularization参数是损失函数的正则化项，对应于【XGBoost】中方程（2）中的$\lambda$。

请注意，如果样本数量大于10,000，则默认情况下启用了提前停止。提前停止的行为由early_stopping、scoring、validation_fraction、n_iter_no_change和tol参数控制。可以使用任意的scorer或仅使用训练或验证损失来进行提前停止。请注意，出于技术原因，使用可调用对象作为评分器比使用损失函数要慢得多。默认情况下，如果训练集中有至少10,000个样本，则执行提前停止，使用验证损失。

缺失值支持

HistGradientBoostingClassifier和HistGradientBoostingRegressor原生支持缺失值（NaN）。

在训练过程中，树生成器会在每个分割点学习样本的缺失值应该进入左子节点还是右子节点，这是基于潜在增益的。在预测时，具有缺失值的样本将被分配给左子节点或右子节点：

>>> from sklearn.ensemble import HistGradientBoostingClassifier
>>> import numpy as np

>>> X = np.array([0, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 0, 1, 1]

>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 0, 1, 1])

当缺失模式具有预测能力时，可以根据特征值是否缺失来进行分割：

>>> X = np.array([0, np.nan, 1, 2, np.nan]).reshape(-1, 1)
>>> y = [0, 1, 0, 0, 1]
>>> gbdt = HistGradientBoostingClassifier(min_samples_leaf=1,
...                                       max_depth=2,
...                                       learning_rate=1,
...                                       max_iter=1).fit(X, y)
>>> gbdt.predict(X)
array([0, 1, 0, 0, 1])

如果在训练过程中某个特征没有遇到缺失值，则具有缺失值的样本将被映射到具有最多样本的子节点。

样本权重支持

HistGradientBoostingClassifier和HistGradientBoostingRegressor在fit过程中支持样本权重。

以下示例说明了具有零样本权重的样本将被忽略：

>>> X = [[1, 0],
...      [1, 0],
...      [1, 0],
...      [0, 1]]
>>> y = [0, 0, 1, 0]
>>> # 通过将前两个训练样本的权重设置为0来忽略它们
>>> sample_weight = [0, 0, 1, 1]
>>> gb = HistGradientBoostingClassifier(min_samples_leaf=1)
>>> gb.fit(X, y, sample_weight=sample_weight)
HistGradientBoostingClassifier(...)
>>> gb.predict([[1, 0]])
array([1])
>>> gb.predict_proba([[1, 0]])[0, 1]
0.99...

如您所见，由于前两个样本的样本权重为零，因此[1, 0]被舒适地分类为1。

实现细节：考虑样本权重相当于将梯度（和海森矩阵）乘以样本权重。请注意，分箱阶段（特别是分位数计算）不考虑权重。

分类特征支持

HistGradientBoostingClassifier和HistGradientBoostingRegressor原生支持分类特征：它们可以考虑非有序的分类数据进行分割。
要启用分类支持，可以将布尔掩码传递给categorical_features参数，指示哪个特征是分类的。以下是将第一个特征视为分类特征，第二个特征视为数值特征的示例：

gbdt = HistGradientBoostingClassifier(categorical_features=[True, False])

同样，可以传递一个整数列表，指示分类特征的索引：

gbdt = HistGradientBoostingClassifier(categorical_features=[0])

当输入是DataFrame时，还可以传递一个列名的列表：

gbdt = HistGradientBoostingClassifier(categorical_features=["site", "manufacturer"])

最后，当输入是DataFrame时，我们可以使用categorical_features="from_dtype"，这样所有具有分类数据类型的列都将被视为分类特征。

每个分类特征的基数必须小于max_bins参数。有关在分类特征上使用基于直方图的梯度提升的示例，请参见sphx_glr_auto_examples_ensemble_plot_gradient_boosting_categorical.py。

如果在训练过程中存在缺失值，则将缺失值视为一个特殊的类别。如果在训练过程中没有缺失值，则在预测时，缺失值将映射到具有最多样本的子节点（与连续特征的处理方式相同）。在预测时，未在拟合时见过的类别将被视为缺失值。

使用分类特征进行分割查找：在树中考虑分类特征的规范方法是考虑所有的$2^{K-1}-1$个分区，其中$K$是类别的数量。当$K$很大时，这可能很快变得不可行。幸运的是，由于梯度提升树始终是回归树（即使用于分类问题），存在一种更快的策略可以得到等效的分割。首先，根据目标的方差对特征的类别进行排序，对于每个类别$k$。一旦类别排序完成，可以考虑连续分区，即将类别视为有序连续值（参见Fisher [Fisher1958]的正式证明）。因此，只需要考虑$K-1$个分割点，而不是$2^{K-1}-1$个。初始排序是一个$\mathcal{O}(K\log (K))$的操作，总复杂度为$\mathcal{O}(K\log (K)+K)$，而不是$\mathcal{O}(2^K)$。

示例：

• sphx_glr_auto_examples_ensemble_plot_gradient_boosting_categorical.py

单调约束

根据手头的问题，您可能具有先验知识，指示给定特征通常对目标值产生正（或负）影响。例如，其他条件相同，较高的信用评分应该增加获得贷款批准的概率。单调约束允许您将这样的先验知识纳入模型中。

对于具有两个特征的预测器$F$：

• 单调增加约束是以下形式的约束：

  $$x_1\le x_1^{\prime }⟹F(x_1,x_2)\le F(x_1^{\prime },x_2)$$

• 单调减少约束是以下形式的约束：

  $$x_1\le x_1^{\prime }⟹F(x_1,x_2)\ge F(x_1^{\prime },x_2)$$

您可以使用monotonic_cst参数在每个特征上指定单调约束。对于每个特征，值为0表示没有约束，而值为1和-1表示单调增加和单调减少约束：

from sklearn.ensemble import HistGradientBoostingRegressor

# 对3个特征分别设置单调增加、单调减少和无约束
gbdt = HistGradientBoostingRegressor(monotonic_cst=[1, -1, 0])

在二分类情况下，施加单调增加（减少）约束意味着特征的较高值应该对样本属于正类的概率产生正（负）影响。

然而，单调约束只对输出的特征影响产生边际约束。例如，单调增加和减少约束不能用于强制执行以下建模约束：

$$x_1\le x_1^{\prime }⟹F(x_1,x_2)\le F(x_1^{\prime },x_2^{\prime })$$

此外，多类分类不支持单调约束。

[!NOTE]
由于类别是无序的量，无法对分类特征施加单调约束。

示例：

• sphx_glr_auto_examples_ensemble_plot_monotonic_constraints.py

交互约束

先验地，直方图梯度提升树允许使用任何特征将节点分割为子节点。这会创建特征之间的交互作用，即在分支上使用不同的特征作为分割。有时，我们希望限制可能的交互作用，参见[Mayer2022]。可以通过interaction_cst参数来实现。其中可以指定允许交互的特征的索引。例如，对于总共3个特征，interaction_cst=[{0}, {1}, {2}]禁止所有交互。约束[{0, 1}, {1, 2}]指定两组可能交互的特征。特征0和1可以相互交互，特征1和2也可以相互交互。但请注意，特征0和2禁止相互交互。下面描述了一棵树和树的可能分割：

1      <- 从现在开始可以应用两个约束组
/ \
1   2    <- 左分割仍然满足两个约束组。
/ \ / \      右分割在特征2上只有约束组{1, 2}。

LightGBM对重叠组使用相同的逻辑。

请注意，未在interaction_cst中列出的特征会自动分配一个独立的交互组。对于再次有3个特征的情况，这意味着[{0}]等效于[{0}, {1, 2}]。

示例：

• sphx_glr_auto_examples_inspection_plot_partial_dependence.py

参考文献

低级并行性

HistGradientBoostingClassifier和HistGradientBoostingRegressor通过Cython使用OpenMP进行并行化。有关如何控制线程数的详细信息，请参阅我们的parallelism说明。

以下部分是并行化的：

• 将实值样本映射到整数值的箱中（找到箱阈值的过程是顺序的）
• 构建直方图在特征上并行化
• 在节点上找到最佳分割点在特征上并行化
• 在拟合过程中，将样本映射到左右子节点在样本上并行化
• 梯度和海森矩阵的计算在样本上并行化
• 预测在样本上并行化

为什么更快

梯度提升过程的瓶颈是构建决策树。构建传统决策树（如其他GBDT中的GradientBoostingClassifier和GradientBoostingRegressor）需要对每个节点的样本进行排序（对于每个特征）。排序是必需的，以便有效地计算分割点的潜在增益。因此，拆分单个节点的复杂度为$\mathcal{O}(n_{\text{features}}\times n\log (n))$，其中$n$是节点上的样本数。

相比之下，HistGradientBoostingClassifier和HistGradientBoostingRegressor不需要对特征值进行排序，而是使用一种称为直方图的数据结构，其中样本被隐式排序。构建直方图的复杂度为$\mathcal{O}(n)$，因此节点分割过程的复杂度为$\mathcal{O}(n_{\text{features}}\times n)$，远小于之前的复杂度。此外，我们只考虑max_bins个分割点，而不是考虑$n$个分割点，这可能要小得多。
最后，HistGradientBoostingClassifier和HistGradientBoostingRegressor的许多实现部分都是并行的。

参考文献

GradientBoostingClassifier和GradientBoostingRegressor

下面介绍了GradientBoostingClassifier和GradientBoostingRegressor的用法和参数。这些估计器的两个最重要的参数是n_estimators和learning_rate。

分类

GradientBoostingClassifier支持二元和多类分类。下面的示例展示了如何使用100个决策树桩作为弱学习器来拟合梯度提升分类器：

from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier

X, y = make_hastie_10_2(random_state=0)
X_train, X_test = X[:2000], X[2000:]
y_train, y_test = y[:2000], y[2000:]

clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
    max_depth=1, random_state=0).fit(X_train, y_train)
clf.score(X_test, y_test)

弱学习器（即回归树）的数量由参数n_estimators控制；可以通过设置树的深度（通过max_depth）或者设置叶节点的数量（通过max_leaf_nodes）来控制每棵树的大小。learning_rate是一个超参数，范围在(0.0, 1.0]之间，通过shrinkage来控制过拟合。

[!NOTE]
对于多于2个类别的分类，每次迭代需要引入n_classes个回归树，因此总共引入的树的数量等于n_classes * n_estimators。对于具有大量类别的数据集，我们强烈建议使用HistGradientBoostingClassifier作为GradientBoostingClassifier的替代方法。

回归

GradientBoostingRegressor支持多种回归的不同损失函数<gradient_boosting_loss>，可以通过参数loss指定；回归的默认损失函数是平方误差（'squared_error'）。

import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor

X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
X_train, X_test = X[:200], X[200:]
y_train, y_test = y[:200], y[200:]
est = GradientBoostingRegressor(
    n_estimators=100, learning_rate=0.1, max_depth=1, random_state=0,
    loss='squared_error'
).fit(X_train, y_train)
mean_squared_error(y_test, est.predict(X_test))

下图显示了将最小二乘损失和500个基学习器应用于糖尿病数据集（sklearn.datasets.load_diabetes）的GradientBoostingRegressor的结果。图中显示了每次迭代的训练误差和测试误差。每次迭代的训练误差存储在梯度提升模型的train_score_属性中。可以通过~GradientBoostingRegressor.staged_predict方法获取每个阶段的预测结果，该方法返回一个生成器。可以使用这样的图来确定树的最佳数量（即n_estimators），通过提前停止来实现。

示例：

• sphx_glr_auto_examples_ensemble_plot_gradient_boosting_regression.py
• sphx_glr_auto_examples_ensemble_plot_gradient_boosting_oob.py

拟合额外的弱学习器

GradientBoostingRegressor和GradientBoostingClassifier都支持warm_start=True，这允许您向已经拟合的模型中添加更多的估计器。

_ = est.set_params(n_estimators=200, warm_start=True)  # 设置warm_start和新的树的数量
_ = est.fit(X_train, y_train) # 向est中添加额外的100棵树
mean_squared_error(y_test, est.predict(X_test))

控制树的大小

回归树基学习器的大小定义了梯度提升模型可以捕捉的变量交互的级别。一般来说，深度为h的树可以捕捉到h阶的交互。有两种方法可以控制每棵回归树的大小。

如果指定max_depth=h，则会生成深度为h的完全二叉树。这样的树将具有（最多）2**h个叶节点和2**h - 1个分割节点。

另一种方法是通过参数max_leaf_nodes指定叶节点的数量来控制树的大小。在这种情况下，将使用最佳优先搜索来生成树，其中具有最大纯度改善的节点将首先展开。具有max_leaf_nodes=k的树有k - 1个分割节点，因此可以模拟最高阶为max_leaf_nodes - 1的交互。

我们发现max_leaf_nodes=k的结果与max_depth=k-1的结果相当，但训练速度明显更快，代价是稍高的训练误差。参数max_leaf_nodes对应于[Friedman2001]中梯度提升章节中的变量J，与R的gbm包中的参数interaction.depth相关，其中max_leaf_nodes == interaction.depth + 1。

数学公式

首先介绍回归的GBRT，然后详细说明分类的情况。

回归

GBRT回归器是一种加法模型，对于给定的输入$x_i$，其预测${\hat{y}}_i$的形式如下：

$${\hat{y}}_i=F_M(x_i)=\sum _{m=1}^M{h}_m(x_i)$$

其中$h_m$是在提升上下文中称为弱学习器的估计器。梯度树提升使用固定大小的决策树回归器<tree>作为弱学习器。常数M对应于n_estimators参数。

与其他提升算法类似，GBRT是以贪婪的方式构建的：

$$F_m(x)=F_{m-1}(x)+h_m(x),$$

其中新添加的树$h_m$被拟合以最小化一系列损失$L_m$，给定先前的集成$F_{m-1}$：

$$h_m=\arg \underset{h}{\min }{L}_m=\arg \underset{h}{\min }\sum _{i=1}^{n}l(y_i,F_{m-1}(x_i)+h(x_i)),$$

其中$l(y_i,F(x_i))$由损失参数定义，详细说明在下一节中。

默认情况下，初始模型$F_0$被选择为最小化损失的常数：对于最小二乘损失，这是目标值的经验均值。初始模型也可以通过init参数指定。

使用一阶泰勒展开，可以近似计算$l$的值如下：

$$
l(y_i, F_{m-1}(x_i) + h_m(x_i)) \approx
l(y_i, F_{m-1}(x_i)

• h_m(x_i)
  \left[ \frac{\partial l(y_i, F(x_i))}{\partial F(x_i)} \right]{F=F{m - 1}}
  $$

[!NOTE]
简单来说，一阶泰勒展开表示$l(z)\approx l(a)+(z-a)\frac{\partial l}{\partial z}(a)$。这里，$z$对应于$F_{m-1}(x_i)+h_m(x_i)$，$a$对应于$F_{m-1}(x_i)$。

量${\left[\frac{\partial l(y_i,F(x_i))}{\partial F(x_i)}\right]}_{F=F_{m-1}}$是损失相对于其第二个参数的导数，在$F_{m-1}(x)$处求值。由于损失是可微的，因此可以很容易地计算出给定$F_{m-1}(x_i)$的导数。我们将其记为$g_i$。

去除常数项，我们有：

$$h_m\approx \arg \underset{h}{\min }\sum _{i=1}^{n}h(x_i)g_i$$

如果$h(x_i)$被拟合为预测与负梯度$-g_i$成比例的值，则可以最小化这个表达式。因此，在每次迭代中，估计器$h_m$被拟合为预测样本的负梯度。梯度在每次迭代中更新。这可以被看作是在函数空间中的一种梯度下降方法。

[!NOTE]

分类

分类问题的梯度提升与回归问题非常相似。然而，树的总和 $F_M(x_i)={\sum }_m{h}_m(x_i)$ 不是一个预测的类别，因为树预测的是连续值。

将 $F_M(x_i)$ 的值映射到类别或概率是与损失函数相关的。对于对数损失函数，$x_i$ 属于正类的概率被建模为 $p(y_i=1|x_i)=\sigma (F_M(x_i))$，其中 $\sigma$ 是 sigmoid 函数。

对于多类分类问题，在每次迭代中，会构建 K 个树（对应 K 个类别）。$x_i$ 属于第 k 类的概率被建模为 $F_{M,k}(x_i)$ 值的 softmax。

需要注意的是，即使是分类任务，$h_m$ 子估计器仍然是一个回归器，而不是分类器。这是因为子估计器被训练来预测（负）梯度，而梯度始终是连续的量。

损失函数

可以使用参数 loss 来指定以下损失函数：

• 回归
  • 平方误差（'squared_error'）：由于其出色的计算性能，这是回归问题的自然选择。初始模型由目标值的均值给出。
  • 绝对误差（'absolute_error'）：用于回归的鲁棒损失函数。初始模型由目标值的中位数给出。
  • Huber（'huber'）：将最小二乘和最小绝对偏差相结合的另一个鲁棒损失函数；使用 alpha 来控制对异常值的敏感性（详见 [Friedman2001]）。
  • 分位数（'quantile'）：用于分位数回归的损失函数。使用 0 < alpha < 1 来指定分位数。该损失函数可用于创建预测区间（详见 sphx_glr_auto_examples_ensemble_plot_gradient_boosting_quantile.py）。
• 分类
  • 二元对数损失（'log-loss'）：用于二元分类的二项式负对数似然损失函数。它提供概率估计。初始模型由对数几率给出。
  • 多类对数损失（'log-loss'）：用于具有 n_classes 个互斥类别的多类分类的多项式负对数似然损失函数。它提供概率估计。初始模型由每个类别的先验概率给出。每次迭代需要构建 n_classes 个回归树，这使得 GBRT 在具有大量类别的数据集上效率较低。
  • 指数损失（'exponential'）：与 AdaBoostClassifier 使用相同的损失函数。对错误标记的示例不太鲁棒，只能用于二元分类。

通过学习率进行收缩

[Friedman2001] 提出了一种简单的正则化策略，通过常数因子 $\nu$ 缩放每个弱学习器的贡献：

$$F_m(x)=F_{m-1}(x)+\nu h_m(x)$$

参数 $\nu$ 也被称为学习率，因为它缩放了梯度下降过程的步长；可以通过 learning_rate 参数设置。

参数 learning_rate 与参数 n_estimators（要拟合的弱学习器的数量）之间有很强的相互作用。较小的 learning_rate 值需要更大数量的弱学习器来保持恒定的训练误差。经验证据表明，较小的 learning_rate 值有利于更好的测试误差。[HTF] 建议将学习率设置为一个小的常数（例如 learning_rate <= 0.1），并选择足够大的 n_estimators 使得早停法适用，详见 sphx_glr_auto_examples_ensemble_plot_gradient_boosting_early_stopping.py 以获取有关 learning_rate 和 n_estimators 之间相互作用的更详细讨论，详见 [R2007]。

子采样

[Friedman2002] 提出了随机梯度提升，它将梯度提升与自助平均（bagging）相结合。在每次迭代中，基分类器在可用训练数据的一部分 subsample 上进行训练。子样本是无放回抽样的。subsample 的典型值为 0.5。

下图说明了收缩和子采样对模型拟合效果的影响。我们可以清楚地看到，收缩优于无收缩。收缩与子采样相结合可以进一步提高模型的准确性。然而，没有收缩的子采样效果较差。

另一种减小方差的策略是类似于 RandomForestClassifier 中的随机特征子采样。可以通过 max_features 参数来控制子采样的特征数量。

[!NOTE]
使用较小的 max_features 值可以显著减少运行时间。

随机梯度提升允许通过计算未包含在自助样本中的示例（即 out-of-bag 示例）上的损失改进来计算测试偏差的 out-of-bag 估计。改进值存储在属性 oob_improvement_ 中。oob_improvement_[i] 表示如果将第 i 个阶段添加到当前预测中，对于 OOB 样本的损失的改进。可以使用 out-of-bag 估计进行模型选择，例如确定最佳迭代次数。OOB 估计通常非常保守，因此我们建议使用交叉验证，并仅在交叉验证耗时过长时使用 OOB。

示例：

• sphx_glr_auto_examples_ensemble_plot_gradient_boosting_regularization.py
• sphx_glr_auto_examples_ensemble_plot_gradient_boosting_oob.py
• sphx_glr_auto_examples_ensemble_plot_ensemble_oob.py

特征重要性的解释

通过简单地可视化树结构，可以轻松地解释单个决策树。然而，梯度提升模型由数百个回归树组成，因此无法通过直观地检查单个树来轻松解释。幸运的是，已经提出了一些技术来总结和解释梯度提升模型。

通常，特征对于预测目标响应的贡献并不相等；在许多情况下，大多数特征实际上是无关的。在解释模型时，通常的第一个问题是：哪些特征是重要的，它们在预测目标响应方面的贡献是什么？

单个决策树通过选择适当的分割点来进行特征选择。这些信息可以用于衡量每个特征的重要性；基本思想是：一个特征在树的分割点中使用的次数越多，该特征就越重要。通过简单地对每棵树的基于不纯度的特征重要性进行平均，可以将这种重要性概念扩展到决策树集合中（详见 random_forest_feature_importance 以获取更多详细信息）。

拟合的梯度提升模型的特征重要性分数可以通过 feature_importances_ 属性进行访问：

>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier

>>> X, y = make_hastie_10_2(random_state=0)
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
...     max_depth=1, random_state=0).fit(X, y)
>>> clf.feature_importances_
array([0.10..., 0.10..., 0.11..., ...

需要注意的是，特征重要性的计算是基于熵的，与基于特征排列的 sklearn.inspection.permutation_importance 不同。

示例：

• sphx_glr_auto_examples_ensemble_plot_gradient_boosting_regression.py

参考文献

随机森林和其他随机树集成方法

与其他分类器一样，随机森林分类器需要用两个数组进行拟合：一个稀疏或密集的形状为 (n_samples, n_features) 的数组 X 保存训练样本，一个形状为 (n_samples,) 的数组 Y 保存训练样本的目标值（类别标签）：

from sklearn.ensemble import RandomForestClassifier
X = [[0, 0], [1, 1]]
Y = [0, 1]
clf = RandomForestClassifier(n_estimators=10)
clf = clf.fit(X, Y)

与决策树一样，树的集合也可以扩展到多输出问题（如果 Y 是一个形状为 (n_samples, n_outputs) 的数组）。

随机森林

在随机森林中（参见 RandomForestClassifier 和 RandomForestRegressor 类），集合中的每棵树都是从训练集中通过有放回抽样（即自助样本）构建的。

此外，在构建树的每个节点时，最佳分割是通过对所有输入特征的特征值或大小为 max_features 的随机子集的特征值进行穷举搜索来找到的（有关详细信息，请参见 参数调整指南 <random_forest_parameters>）。

这两种随机性的目的是减小森林估计器的方差。事实上，单个决策树通常表现出较高的方差并且容易过拟合。在森林中注入随机性可以产生具有相对独立预测误差的决策树。通过对这些预测值取平均，一些误差可以相互抵消。随机森林通过组合不同的树来减小方差，有时会稍微增加偏差。实际上，方差的减小通常是显著的，从而产生一个整体上更好的模型。

与原始出版物 [B2001] 不同的是，scikit-learn 的实现通过对概率预测进行平均，而不是让每个分类器为单个类别投票。

与随机森林相竞争的替代方法是基于直方图的梯度提升（HGBT）模型：

• 构建树：随机森林通常依赖于深树（单独过拟合），这需要大量的计算资源，因为它们需要进行多次分割和候选分割的评估。提升模型构建浅树（单独欠拟合），更容易拟合和预测。
• 顺序提升：在 HGBT 中，决策树是顺序构建的，每棵树都被训练以纠正前面树所犯的错误。这使得它们可以通过相对较少的树迭代改进模型的性能。相比之下，随机森林使用多数投票来预测结果，这可能需要更多的树才能达到相同的准确性水平。
• 高效分箱：HGBT 使用一种高效的分箱算法，可以处理具有大量特征的大型数据集。分箱算法可以预处理数据以加速后续的树构建（参见 为什么更快 <Why_it's_faster>）。相比之下，scikit-learn 的随机森林实现不使用分箱，而是依赖于精确分割，这可能需要较长的计算时间。

总的来说，HGBT 相对于 RF 的计算成本取决于数据集和建模任务的特定特征。在特定问题上尝试两种模型并比较它们的性能和计算效率，以确定哪种模型最适合。

示例：

• sphx_glr_auto_examples_ensemble_plot_forest_hist_grad_boosting_comparison.py

极端随机树

在极端随机树中（参见 ExtraTreesClassifier 和 ExtraTreesRegressor 类），随机性在计算分割时更进一步。与随机森林一样，使用了候选特征的随机子集，但是不是寻找最具有区分度的阈值，而是为每个候选特征随机选择阈值，并从这些随机生成的阈值中选择最佳的作为分割规则。这通常可以进一步减小模型的方差，但代价是稍微增加了偏差：

from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.tree import DecisionTreeClassifier

X, y = make_blobs(n_samples=10000, n_features=10, centers=100, random_state=0)

clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2, random_state=0)
scores = cross_val_score(clf, X, y, cv=5)
scores.mean()

clf = RandomForestClassifier(n_estimators=10, max_depth=None, min_samples_split=2, random_state=0)
scores = cross_val_score(clf, X, y, cv=5)
scores.mean()

clf = ExtraTreesClassifier(n_estimators=10, max_depth=None, min_samples_split=2, random_state=0)
scores = cross_val_score(clf, X, y, cv=5)
scores.mean() > 0.999

参数

使用这些方法时要调整的主要参数是 n_estimators 和 max_features。前者是森林中的树的数量。数量越多越好，但计算时间也会更长。此外，需要注意的是，在关键树的数量之后，结果将不会显著改善。后者是在分割节点时要考虑的特征的随机子集的大小。减小此值可以减小方差，但也会增加偏差。经验性的好的默认值是 max_features=1.0 或等价的 max_features=None（始终考虑所有特征而不是随机子集）用于回归问题，以及 max_features="sqrt"（使用大小为 sqrt(n_features) 的随机子集）用于分类任务（其中 n_features 是数据中的特征数量）。max_features=1.0 的默认值等同于袋装树，通过设置较小的值（例如 0.3 是文献中的典型默认值）可以实现更多的随机性。通常在完全发展树时将 max_depth=None 与 min_samples_split=2 结合使用可以获得良好的结果。但请记住，这些值通常不是最优的，并且可能导致消耗大量内存的模型。最佳参数值应始终进行交叉验证。此外，需要注意的是，在随机森林中，默认情况下使用自助样本（bootstrap=True），而额外树的默认策略是使用整个数据集（bootstrap=False）。使用自助采样可以在留出样本或袋外样本上估计泛化误差。可以通过设置 oob_score=True 来启用此功能。

[!NOTE]
默认参数的模型大小为 $O(M\ast N\ast log(N))$，其中 $M$ 是树的数量，$N$ 是样本的数量。为了减小模型的大小，可以更改这些参数：min_samples_split、max_leaf_nodes、max_depth 和 min_samples_leaf。

并行化

最后，该模块还通过 n_jobs 参数实现了树的并行构建和预测的并行计算。如果 n_jobs=k，则计算被分成 k 个作业，并在机器的 k 个核上运行。如果 n_jobs=-1，则使用机器上所有可用的核。请注意，由于进程间通信开销，加速可能不是线性的（即，使用 k 个作业不会以 k 倍的速度运行）。然而，在构建大量树或构建单棵树需要相当长时间（例如，在大型数据集上）时，仍然可以实现显著的加速。

示例：

• sphx_glr_auto_examples_ensemble_plot_forest_iris.py

特征重要性评估

在决策树中，作为决策节点使用的特征的相对排名（即深度）可以用来评估该特征相对于目标变量的可预测性的重要性。在树的顶部使用的特征对输入样本的最终预测决策有更大的贡献。因此，它们对样本的贡献的期望比例可以用作特征重要性的估计。在scikit-learn中，特征对样本的贡献的比例与从分裂它们中减少的不纯度结合在一起，创建了该特征预测能力的归一化估计。

通过对几个随机化树的预测能力估计进行平均，可以减小估计的方差并将其用于特征选择。这被称为不纯度的平均减少，或者MDI。有关MDI和随机森林中特征重要性评估的更多信息，请参考[20]。

[!WARNING]
基于不纯度的特征重要性计算在基于树的模型上存在两个缺陷，可能导致误导性结论。首先，它们是基于训练数据集导出的统计数据计算的，因此不一定能告诉我们哪些特征对于在保留数据集上进行良好预测最重要。其次，它们偏爱高基数特征，即具有许多唯一值的特征。permutation_importance是一种替代基于不纯度的特征重要性的方法，它不会受到这些缺陷的影响。这两种获取特征重要性的方法在sphx_glr_auto_examples_inspection_plot_permutation_importance.py中进行了探讨。

下面的示例展示了使用ExtraTreesClassifier模型进行人脸识别任务时，每个像素的相对重要性的彩色表示。

在实践中，这些预测能力的估计值存储在已拟合模型的feature_importances_属性中。这是一个形状为(n_features,)的数组，其值为正数且总和为1.0。值越高，匹配特征对预测函数的贡献越重要。

示例：

• sphx_glr_auto_examples_ensemble_plot_forest_importances_faces.py
• sphx_glr_auto_examples_ensemble_plot_forest_importances.py

完全随机树嵌入

RandomTreesEmbedding实现了一种无监督的数据转换。使用一组完全随机的树，RandomTreesEmbedding通过数据点最终所在的叶子节点的索引对数据进行编码。然后，将该索引以一对K的方式进行编码，从而得到一个高维、稀疏的二进制编码。这种编码可以非常高效地计算，并且可以用作其他学习任务的基础。代码的大小和稀疏性可以通过选择树的数量和每棵树的最大深度来影响。对于集合中的每棵树，编码包含一个条目为1的条目。编码的大小最多为n_estimators * 2 ** max_depth，即森林中叶子的最大数量。

由于相邻的数据点更有可能位于树的同一叶子中，因此该转换执行了一种隐式的、非参数的密度估计。

示例：

• sphx_glr_auto_examples_ensemble_plot_random_forest_embedding.py
• sphx_glr_auto_examples_manifold_plot_lle_digits.py比较了手写数字上的非线性降维技术。
• sphx_glr_auto_examples_ensemble_plot_feature_transformation.py比较了基于树的有监督和无监督特征转换。

manifold技术也可以用于推导特征空间的非线性表示，这些方法也侧重于降维。

Bagging元估计器

在集成算法中，bagging方法是一类算法，它在原始训练集的随机子集上构建多个黑盒估计器的实例，然后将它们的个体预测聚合起来形成最终的预测。这些方法被用作减小基本估计器（例如决策树）的方差的一种方式，通过将随机性引入其构建过程，然后将其组合成一个集合。在许多情况下，bagging方法构成了相对于单个模型改进的一种非常简单的方法，而不需要调整基础算法。由于它们提供了一种减少过拟合的方法，bagging方法在强大且复杂的模型（例如完全发展的决策树）上效果最好，与提升方法相反，提升方法通常在弱模型（例如浅层决策树）上效果最好。

Bagging方法有多种变体，但主要区别在于它们如何从训练集中抽取随机子集：

• 当将数据集的随机子集作为样本的随机子集时，该算法被称为Pasting [B1999]。
• 当使用替换抽样时，该方法被称为Bagging [B1996]。
• 当将数据集的随机子集作为特征的随机子集时，该方法被称为Random Subspaces [H1998]。
• 最后，当基本估计器在样本和特征的子集上构建时，该方法被称为Random Patches [LG2012]。

在scikit-learn中，bagging方法作为统一的BaggingClassifier元估计器（或BaggingRegressor）提供，用户可以指定一个估计器以及指定绘制随机子集策略的参数。特别地，max_samples和max_features控制子集的大小（以样本和特征为单位），而bootstrap和bootstrap_features控制是否使用替换抽样绘制样本和特征。当使用可用样本的子集时，可以通过设置oob_score=True来使用out-of-bag样本估计泛化准确性。例如，下面的代码片段演示了如何实例化一个~sklearn.neighbors.KNeighborsClassifier估计器的bagging集合，每个估计器都是在50%的样本和50%的特征的随机子集上构建的。

>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.neighbors import KNeighborsClassifier
>>> bagging = BaggingClassifier(KNeighborsClassifier(),
...                             max_samples=0.5, max_features=0.5)

示例：

• sphx_glr_auto_examples_ensemble_plot_bias_variance.py

参考文献

投票分类器

VotingClassifier的思想是结合概念上不同的机器学习分类器，并使用多数投票或平均预测概率（软投票）来预测类标签。这样的分类器对于一组表现相同的模型来说是有用的，以平衡它们各自的弱点。

多数类标签（多数/硬投票）

在多数投票中，对于特定样本的预测类标签是由每个单独分类器预测的类标签中占多数（众数）的类标签。

例如，如果给定样本的预测如下：

• 分类器1 -> 类别1
• 分类器2 -> 类别1
• 分类器3 -> 类别2

使用VotingClassifier（voting='hard'）将基于多数类标签将样本分类为“类别1”。

在平局的情况下，VotingClassifier将根据升序排序顺序选择类别。例如，在以下场景中：

• 分类器1 -> 类别2
• 分类器2 -> 类别1

将分配类别标签1给样本。

用法

下面的示例展示了如何拟合多数规则分类器：

>>> from sklearn import datasets

加权平均概率（软投票）

与多数投票（硬投票）相反，软投票返回的类标签是预测概率之和的 argmax。

可以通过 weights 参数为每个分类器分配特定的权重。当提供了权重时，收集每个分类器的预测类概率，乘以分类器的权重，并进行平均。最终的类标签是根据平均概率最高的类标签确定的。

为了用一个简单的例子来说明这一点，假设我们有3个分类器和一个3类分类问题，我们给所有分类器分配相等的权重：w1=1，w2=1，w3=1。

则样本的加权平均概率计算如下：

分类器	类别 1	类别 2	类别 3
分类器 1	w1 * 0.2	w1 * 0.5	w1 * 0.3
分类器 2	w2 * 0.6	w2 * 0.3	w2 * 0.1
分类器 3	w3 * 0.3	w3 * 0.4	w3 * 0.3
加权平均概率	0.37	0.4	0.23

在这里，预测的类标签是2，因为它具有最高的平均概率。

下面的例子说明了当使用基于线性支持向量机、决策树和K最近邻分类器的软投票 VotingClassifier 时，决策区域可能会发生变化：

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from itertools import product
from sklearn.ensemble import VotingClassifier

# 加载一些示例数据
iris = datasets.load_iris()
X = iris.data[:, [0, 2]]
y = iris.target

# 训练分类器
clf1 = DecisionTreeClassifier(max_depth=4)
clf2 = KNeighborsClassifier(n_neighbors=7)
clf3 = SVC(kernel='rbf', probability=True)
eclf = VotingClassifier(estimators=[('dt', clf1), ('knn', clf2), ('svc', clf3)],
                        voting='soft', weights=[2, 1, 2])

clf1 = clf1.fit(X, y)
clf2 = clf2.fit(X, y)
clf3 = clf3.fit(X, y)
eclf = eclf.fit(X, y)

使用 GridSearchCV 的 VotingClassifier

VotingClassifier 还可以与 ~sklearn.model_selection.GridSearchCV 结合使用，以调整各个估计器的超参数：

from sklearn.model_selection import GridSearchCV
clf1 = LogisticRegression(random_state=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
eclf = VotingClassifier(
    estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
    voting='soft'
)

params = {'lr__C': [1.0, 100.0], 'rf__n_estimators': [20, 200]}

grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
grid = grid.fit(iris.data, iris.target)

使用 VotingClassifier 进行预测

为了基于预测的类概率预测类标签（scikit-learn 估计器在 VotingClassifier 中必须支持 predict_proba 方法）：

eclf = VotingClassifier(
    estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
    voting='soft'
)

可选地，可以为各个分类器提供权重：

eclf = VotingClassifier(
    estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)],
    voting='soft', weights=[2,5,1]
)

投票回归器

VotingRegressor 的思想是结合概念上不同的机器学习回归器，并返回平均预测值。这样的回归器对于一组表现相同的模型来说是有用的，以平衡它们各自的弱点。

使用方法

以下示例显示了如何拟合 VotingRegressor：

from sklearn.datasets import load_diabetes
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import VotingRegressor

# 加载一些示例数据
X, y = load_diabetes(return_X_y=True)

# 训练回归器
reg1 = GradientBoostingRegressor(random_state=1)
reg2 = RandomForestRegressor(random_state=1)
reg3 = LinearRegression()
ereg = VotingRegressor(estimators=[('gb', reg1), ('rf', reg2), ('lr', reg3)])
ereg = ereg.fit(X, y)

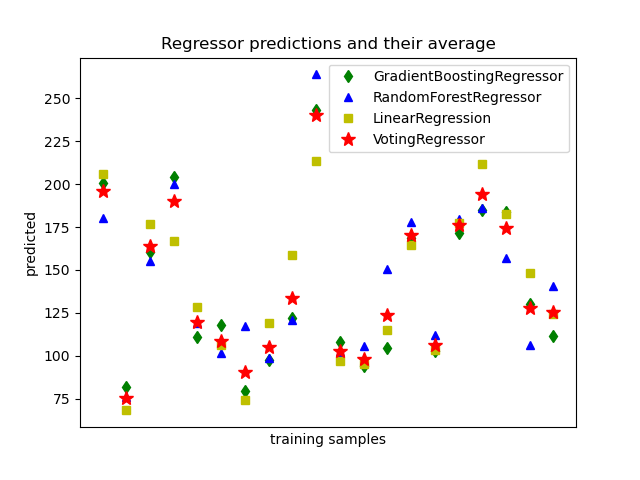
示例：

• sphx_glr_auto_examples_ensemble_plot_voting_regressor.py

堆叠泛化

堆叠泛化是一种将估计器组合起来以减小其偏差的方法[W1992] [HTF]。更具体地说，每个单独估计器的预测被堆叠在一起，作为最终估计器的输入来计算预测。这个最终估计器是通过交叉验证训练的。

StackingClassifier 和 StackingRegressor 提供了这样的策略，可以应用于分类和回归问题。

estimators 参数对应于在输入数据上并行堆叠在一起的估计器列表。它应该作为名称和估计器的列表给出：

from sklearn.linear_model import RidgeCV, LassoCV
from sklearn.neighbors import KNeighborsRegressor
estimators = [('ridge', RidgeCV()),
              ('lasso', LassoCV(random_state=42)),
              ('knr', KNeighborsRegressor(n_neighbors=20,
                                          metric='euclidean'))]

final_estimator 将使用估计器的预测作为输入。当使用 StackingClassifier 或 StackingRegressor 时，它需要是一个分类器或回归器：

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import StackingRegressor
final_estimator = GradientBoostingRegressor(
    n_estimators=25, subsample=0.5, min_samples_leaf=25, max_features=1,
    random_state=42)
reg = StackingRegressor(
    estimators=estimators,
    final_estimator=final_estimator)

要训练估计器和 final_estimator，需要在训练数据上调用 fit 方法：

from sklearn.datasets import load_diabetes
X, y = load_diabetes(return_X_y=True)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
                                                    random_state=42)
reg.fit(X_train, y_train)

在训练过程中，估计器会在整个训练数据 X_train 上进行拟合。在调用 predict 或 predict_proba 时会使用这些估计器。为了泛化和避免过拟合，final_estimator 会在外部样本上使用 sklearn.model_selection.cross_val_predict 进行训练。

对于 StackingClassifier，请注意 estimators 的输出由 stack_method 参数控制，并由每个估计器调用。该参数可以是一个字符串，表示估计器的方法名称，或者是 ‘auto’，它会根据可用性自动识别一个可用的方法，按照以下优先顺序进行测试：predict_proba、decision_function 和 predict。

StackingRegressor 和 StackingClassifier 可以像其他回归器或分类器一样使用，提供 predict、predict_proba 和 decision_function 方法，例如：

y_pred = reg.predict(X_test)
from sklearn.metrics import r2_score
print('R2 score: {:.2f}'.format(r2_score(y_test, y_pred)))

请注意，还可以使用 transform 方法获取堆叠估计器的输出：

reg.transform(X_test[:5])
array([[142..., 138..., 146...],
       [179..., 182..., 151...],
       [139..., 132..., 158...],
       [286..., 292..., 225...],
       [126..., 124..., 164...]])

在实践中，堆叠预测器的预测效果与基层中最好的预测器一样好，甚至有时通过结合这些预测器的不同优势而超越它。然而，训练堆叠预测器的计算成本很高。

[!NOTE]
对于 StackingClassifier，当使用 stack_method=‘predict_proba’ 时，二分类问题的第一列会被丢弃。实际上，每个估计器预测的两列概率是完全共线的。

[!NOTE]
可以通过将 final_estimator 分配给 StackingClassifier 或 StackingRegressor 来实现多个堆叠层：

final_layer_rfr = RandomForestRegressor(
    n_estimators=10, max_features=1, max_leaf_nodes=5, random_state=42)
final_layer_gbr = GradientBoostingRegressor(
    n_estimators=10, max_features=1, max_leaf_nodes=5, random_state=42)
final_layer = StackingRegressor(
    estimators=[('rf', final_layer_rfr), ('gbrt', final_layer_gbr)],
    final_estimator=RidgeCV())
multi_layer_regressor = StackingRegressor(
    estimators=[('ridge', RidgeCV()), ('lasso', LassoCV(random_state=42)),
                ('knr', KNeighborsRegressor(n_neighbors=20, metric='euclidean'))],
    final_estimator=final_layer)
multi_layer_regressor.fit(X_train, y_train)
print('R2 score: {:.2f}'.format(multi_layer_regressor.score(X_test, y_test)))

参考文献

AdaBoost

sklearn.ensemble 模块包括了 1995 年由 Freund 和 Schapire 引入的流行的提升算法 AdaBoost [FS1995]。

AdaBoost 的核心原理是在经过重复修改的数据版本上拟合一系列弱学习器（即，仅比随机猜测稍好的模型，如小型决策树）。然后通过加权多数投票（或求和）将所有弱学习器的预测组合起来得到最终预测。在每个所谓的提升迭代中，对训练样本应用权重 $w_1$、$w_2$、…、$w_N$ 进行数据修改。最初，这些权重都设置为 $w_i=1/N$，因此第一步只是在原始数据上训练一个弱学习器。对于每个后续迭代，样本权重会被单独修改，并且学习算法会重新应用于重新加权的数据。在给定的步骤中，那些在前一步引入的提升模型中被错误预测的训练示例的权重增加，而对于被正确预测的示例，权重减少。随着迭代的进行，难以预测的示例会获得越来越大的影响力。因此，每个后续的弱学习器被迫集中在前面的学习器序列中错过的示例上 [HTF]。

AdaBoost 可以用于分类和回归问题：

• 对于多类分类，AdaBoostClassifier 实现了 AdaBoost.SAMME [ZZRH2009]。
• 对于回归，AdaBoostRegressor 实现了 AdaBoost.R2 [D1997]。

用法

以下示例展示了如何使用 100 个弱学习器拟合 AdaBoost 分类器：

from sklearn.model_selection import cross_val_score
from sklearn.datasets import load_iris
from sklearn.ensemble import AdaBoostClassifier

X, y = load_iris(return_X_y=True)
clf = AdaBoostClassifier(n_estimators=100, algorithm="SAMME")
scores = cross_val_score(clf, X, y, cv=5)
scores.mean()

弱学习器的数量由参数 n_estimators 控制。learning_rate 参数控制弱学习器在最终组合中的贡献。默认情况下，弱学习器是决策树桩。可以通过 estimator 参数指定不同的弱学习器。要获得良好的结果，主要调整的参数是 n_estimators 和基本估计器的复杂度（例如，其深度 max_depth 或要考虑拆分的最小样本数 min_samples_split）。

示例：

• sphx_glr_auto_examples_ensemble_plot_adaboost_multiclass.py 展示了 AdaBoost 在多类问题上的性能。
• sphx_glr_auto_examples_ensemble_plot_adaboost_twoclass.py 展示了使用 AdaBoost-SAMME 在非线性可分的二类问题上的决策边界和决策函数值。
• sphx_glr_auto_examples_ensemble_plot_adaboost_regression.py 演示了使用 AdaBoost.R2 算法进行回归。

参考文献

[FS1995]

Y. Freund 和 R. Schapire，“A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting”，1997。

[ZZRH2009]

J. Zhu、H. Zou、S. Rosset 和 T. Hastie，“Multi-class AdaBoost”，2009。

[D1997]

Drucker，“Improving Regressors using Boosting Techniques”，1997。

[HTF] (1,2,3)

T. Hastie、R. Tibshirani 和 J. Friedman，“Elements of Statistical Learning Ed. 2”，Springer，2009。