Scikit-Learn 1.4使用指南：无监督学习 流形学习 Manifold learning

引用

寻找基本的东西
简单的基本的东西
忘掉你的烦恼和纷争
我说的是基本的东西
大自然的配方
带来生活的基本需求

        -- 巴鲁的歌 \[《森林王子》\]

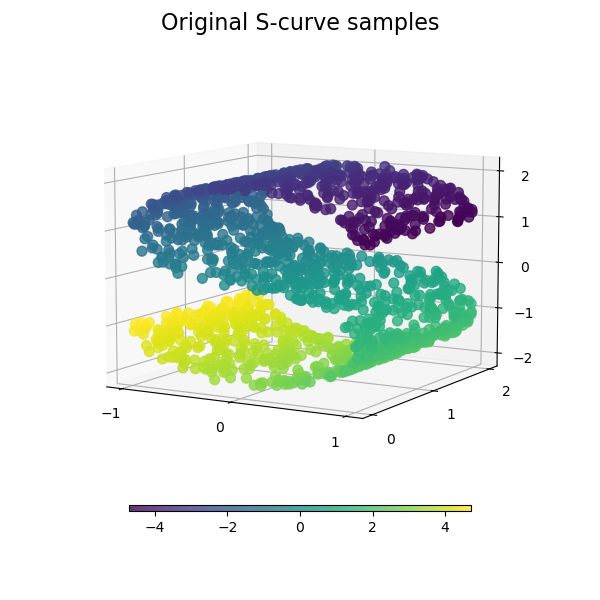
流形学习是一种非线性降维的方法。该任务的算法基于一个观点，即许多数据集的维度只是人为地变高了。

引言

高维数据集很难可视化。虽然可以绘制二维或三维数据以显示数据的内在结构，但等效的高维图往往不太直观。为了帮助可视化数据集的结构，必须以某种方式降低维度。

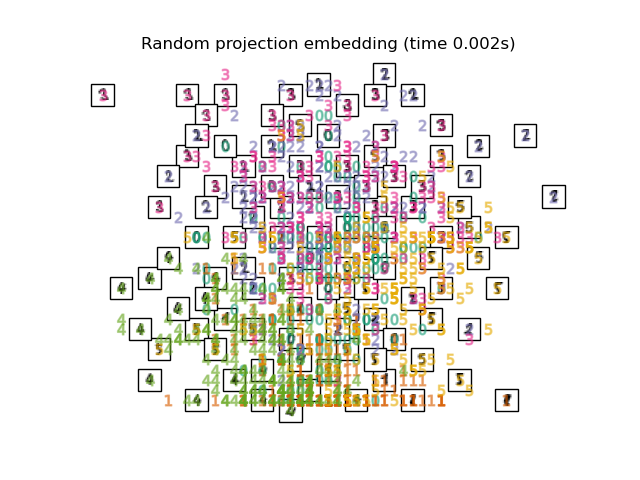
最简单的降维方法是对数据进行随机投影。虽然这样可以在一定程度上可视化数据结构，但是随机选择的不确定性会导致结果不尽如人意。在随机投影中，数据中更有趣的结构很可能会丢失。

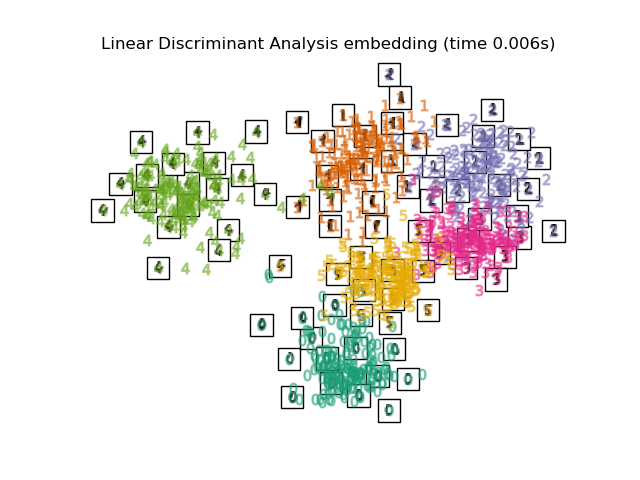
为了解决这个问题，设计了许多有监督和无监督的线性降维框架，例如主成分分析（PCA）、独立成分分析、线性判别分析等。这些算法定义了特定的规则来选择数据的“有趣”线性投影。这些方法可能很强大，但往往会忽略数据中重要的非线性结构。

流形学习可以被看作是将类似PCA的线性框架推广到对数据中的非线性结构敏感的尝试。虽然存在有监督的变体，但典型的流形学习问题是无监督的：它从数据本身中学习数据的高维结构，而不使用预先确定的分类。

示例：

• 请参阅sphx_glr_auto_examples_manifold_plot_lle_digits.py，了解手写数字的降维示例。
• 请参阅sphx_glr_auto_examples_manifold_plot_compare_methods.py，了解玩具“S曲线”数据集的降维示例。

scikit-learn中可用的流形学习实现如下所示

Isomap

流形学习的最早方法之一是Isomap算法，即等距映射。Isomap可以看作是多维缩放（MDS）或核主成分分析的扩展。Isomap寻求一个保持所有点之间测地距离的低维嵌入。可以使用Isomap对象执行Isomap。

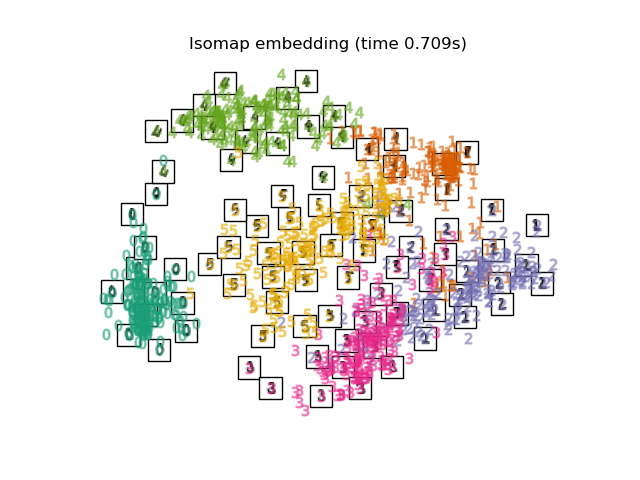
复杂度

Isomap算法包括三个阶段：

1. 最近邻搜索。Isomap使用~sklearn.neighbors.BallTree进行高效的最近邻搜索。成本约为$O[D\log (k)N\log (N)]$，其中$N$是$D$维数据中$N$个点的$k$个最近邻。
2. 最短路径图搜索。目前已知的最有效的算法是Dijkstra算法，其复杂度约为$O[N^2(k+\log (N))]$，或者Floyd-Warshall算法，其复杂度为$O[N^3]$。用户可以使用Isomap的path_method关键字选择算法。如果未指定，代码将尝试选择最适合输入数据的算法。
3. 部分特征值分解。嵌入被编码在与$N\times N$ Isomap核的$d$个最大特征值对应的特征向量中。对于稠密求解器，成本约为$O[d{N}^2]$。可以使用ARPACK求解器来改进这个成本。用户可以使用Isomap的eigen_solver关键字指定特征值求解器。如果未指定，代码将尝试选择最适合输入数据的算法。

Isomap的总体复杂度为$O[D\log (k)N\log (N)]+O[N^2(k+\log (N))]+O[d{N}^2]$。

• $N$：训练数据点的数量
• $D$：输入维度
• $k$：最近邻的数量
• $d$：输出维度

参考文献：

• “A global geometric framework for nonlinear dimensionality reduction” Tenenbaum, J.B.; De Silva, V.; & Langford, J.C. Science 290 (5500)

局部线性嵌入

局部线性嵌入（LLE）寻求数据的低维投影，以保持局部邻域内的距离。可以将其看作是一系列局部主成分分析的全局比较，以找到最佳的非线性嵌入。

可以使用函数locally_linear_embedding或面向对象的LocallyLinearEmbedding执行局部线性嵌入。

复杂度

标准LLE算法包括三个阶段：

1. 最近邻搜索。请参阅上面的Isomap讨论。
2. 权重矩阵构建。$O[DN{k}^3]$。LLE权重矩阵的构建涉及解决每个局部邻域的$k\times k$线性方程组。
3. 部分特征值分解。请参阅上面的Isomap讨论。

标准LLE的总体复杂度为$O[D\log (k)N\log (N)]+O[DN{k}^3]+O[d{N}^2]$。

• $N$：训练数据点的数量
• $D$：输入维度
• $k$：最近邻的数量
• $d$：输出维度

参考文献：

• “Nonlinear dimensionality reduction by locally linear embedding” Roweis, S. & Saul, L. Science 290:2323 (2000)

修改的局部线性嵌入

LLE的一个众所周知的问题是正则化问题。当邻居的数量大于输入维度的数量时，定义每个局部邻域的矩阵是秩亏的。为了解决这个问题，标准LLE应用了一个任意的正则化参数$r$，该参数相对于局部权重矩阵的迹被选择。虽然可以正式地证明，当$r\to 0$时，解收敛到所需的嵌入，但不能保证在$r>0$时找到最优解。这个问题表现为扭曲流形的嵌入。

解决正则化问题的一种方法是在每个邻域中使用多个权重向量。这就是修改的局部线性嵌入（MLLE）的本质。可以使用函数locally_linear_embedding或面向对象的LocallyLinearEmbedding，并使用关键字method = 'modified'执行MLLE。它要求n_neighbors > n_components。

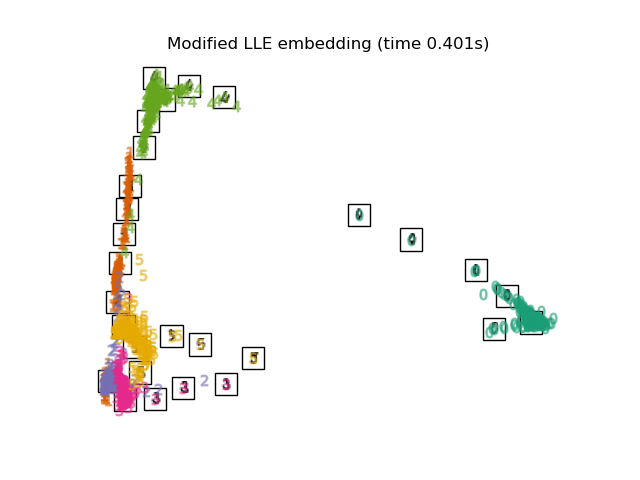
复杂度

MLLE算法包括三个阶段：

2. 权重矩阵构建。大约需要 $O[DN{k}^3]+O[N(k-D)k^2]$ 的时间复杂度。第一项与标准 LLE 相同。第二项与从多个权重构建权重矩阵有关。实际上，构建 MLLE 权重矩阵的额外成本相对于阶段 1 和阶段 3 的成本来说是相对较小的。

3. 部分特征值分解。与标准 LLE 相同。

MLLE 的总体复杂度为 $O[D\log (k)N\log (N)]+O[DN{k}^3]+O[N(k-D)k^2]+O[d{N}^2]$。

• $N$：训练数据点的数量
• $D$：输入维度
• $k$：最近邻的数量
• $d$：输出维度

参考文献：

• “MLLE: Modified Locally Linear Embedding Using Multiple Weights” 张智 & 王健。

Hessian Eigenmapping

Hessian Eigenmapping（也称为基于 Hessian 的 LLE：HLLE）是解决 LLE 正则化问题的另一种方法。它围绕每个邻域的基于 Hessian 的二次形式展开，用于恢复局部线性结构。尽管其他实现指出它在数据规模上的扩展性较差，但 sklearn 实现了一些算法改进，使其成本与其他 LLE 变体相比在小输出维度上可比。HLLE 可以使用函数 locally_linear_embedding 或其面向对象的对应项 LocallyLinearEmbedding 进行计算，关键字为 method = 'hessian'。它要求 n_neighbors > n_components * (n_components + 3) / 2。

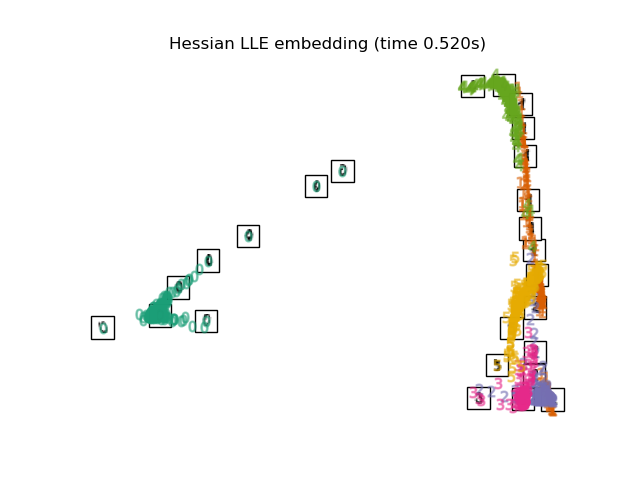
复杂度

HLLE 算法包括三个阶段：

1. 最近邻搜索。与标准 LLE 相同。
2. 权重矩阵构建。大约需要 $O[DN{k}^3]+O[N{d}^6]$ 的时间复杂度。第一项反映了与标准 LLE 相似的成本。第二项来自局部 Hessian 估计的 QR 分解。
3. 部分特征值分解。与标准 LLE 相同。

标准 HLLE 的总体复杂度为 $O[D\log (k)N\log (N)]+O[DN{k}^3]+O[N{d}^6]+O[d{N}^2]$。

• $N$：训练数据点的数量
• $D$：输入维度
• $k$：最近邻的数量
• $d$：输出维度

参考文献：

• “Hessian Eigenmaps: Locally linear embedding techniques for high-dimensional data” Donoho, D. & Grimes, C. Proc Natl Acad Sci USA. 100:5591 (2003)

谱嵌入

谱嵌入是一种计算非线性嵌入的方法。Scikit-learn 实现了拉普拉斯特征映射（Laplacian Eigenmaps），它使用图拉普拉斯特征分解来找到数据的低维表示。生成的图可以被视为高维空间中低维流形的离散近似。基于图的代价函数的最小化确保了在低维空间中，接近的点在局部距离上也是接近的，从而保持了局部距离。可以使用函数 spectral_embedding 或其面向对象的对应项 SpectralEmbedding 进行谱嵌入。

复杂度

谱嵌入（拉普拉斯特征映射）算法包括三个阶段：

1. 加权图构建。使用相似性（邻接）矩阵将原始输入数据转换为图表示。
2. 图拉普拉斯矩阵构建。未归一化的图拉普拉斯矩阵构建为 $L=D-A$，归一化的图拉普拉斯矩阵构建为 $L=D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}$。
3. 部分特征值分解。对图拉普拉斯矩阵进行特征值分解。

谱嵌入的总体复杂度为 $O[D\log (k)N\log (N)]+O[DN{k}^3]+O[d{N}^2]$。

• $N$：训练数据点的数量
• $D$：输入维度
• $k$：最近邻的数量
• $d$：输出维度

参考文献：

• “Laplacian Eigenmaps for Dimensionality Reduction and Data Representation” Belkin, P. Niyogi, Neural Computation, June 2003; 15 (6):1373-1396

局部切空间对齐

虽然局部切空间对齐（LTSA）在技术上不是 LLE 的变体，但它与 LLE 在算法上非常相似，因此可以归类到这个类别中。LTSA 不像 LLE 那样专注于保持邻域距离，而是通过其切空间来表征每个邻域的局部几何，并进行全局优化以对齐这些局部切空间以学习嵌入。可以使用函数 locally_linear_embedding 或其面向对象的对应项 LocallyLinearEmbedding 进行 LTSA 计算，关键字为 method = 'ltsa'。

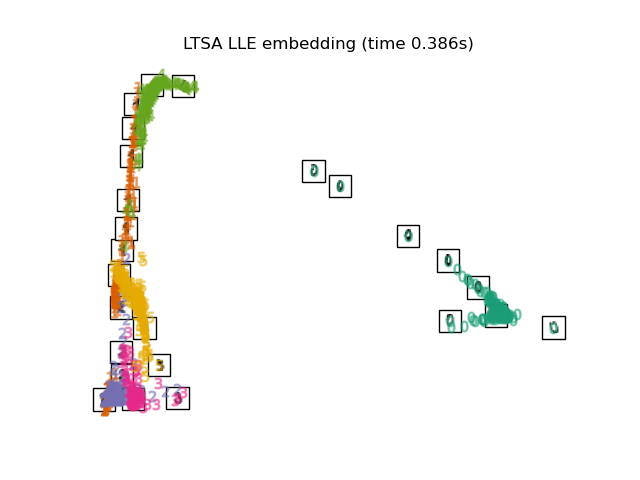
复杂度

LTSA 算法包括三个阶段：

1. 最近邻搜索。与标准 LLE 相同。
2. 权重矩阵构建。大约需要 $O[DN{k}^3]+O[k^{2}d]$ 的时间复杂度。第一项反映了与标准 LLE 相似的成本。
3. 部分特征值分解。与标准 LLE 相同。

标准 LTSA 的总体复杂度为 $O[D\log (k)N\log (N)]+O[DN{k}^3]+O[k^{2}d]+O[d{N}^2]$。

• $N$：训练数据点的数量
• $D$：输入维度
• $k$：最近邻的数量
• $d$：输出维度

参考文献：

• [“Principal manifolds and nonlinear dimensionality reduction via
  tangent space alignment”
  <cs/0212008>` Zhang, Z. & Zha, H. Journal of Shanghai Univ. 8:406 (2004)

多维缩放（MDS）

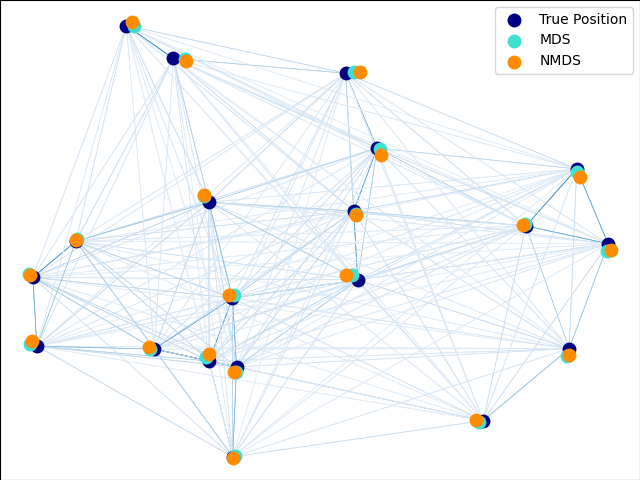
多维缩放（MDS）是一种寻找数据的低维表示，使得低维空间中的距离与原始高维空间中的距离相符的技术。

一般来说，MDS 是一种用于分析相似性或非相似性数据的技术。它试图将相似性或非相似性数据建模为几何空间中的距离。数据可以是对象之间的相似性评级、分子之间的相互作用频率或国家之间的贸易指数。

存在两种类型的 MDS 算法：度量型和非度量型。在 scikit-learn 中，类 MDS 实现了这两种算法。在度量型 MDS 中，输入的相似性矩阵来自度量（因此满足三角不等式），然后将输出两个点之间的距离设置为尽可能接近相似性或非相似性数据。在非度量型 MDS 中，算法将尝试保持距离的顺序，并寻求嵌入空间中的距离与相似性/非相似性之间的单调关系。

设 $S$ 为相似性矩阵，$X$ 为 $n$ 个输入点的坐标。离差 ${\hat{d}}_{ij}$ 是相似性的某种最优转换。目标函数称为应力，定义为 ${\sum }_{i<j}{d}_{ij}(X)-{\hat{d}}_{ij}(X)$。

度量型 MDS

最简单的度量型 MDS 模型称为绝对 MDS，离差由 ${\hat{d}}_{ij}=S_{ij}$ 定义。使用绝对 MDS，值 $S_{ij}$ 应该与嵌入点中点 $i$ 和 $j$ 之间的距离完全对应。

最常见的做法是将离差设置为 ${\hat{d}}_{ij}=b{S}_{ij}$。

非度量型 MDS

非度量型 MDS 关注的是数据的排序。如果 $S_{ij}>S_{jk}$，则嵌入应强制执行 $d_{ij}<d_{jk}$。因此，我们将其从相似性（$S_{ij}$）转换为非相似性（${\delta }_{ij}$）来讨论。请注意，可以通过简单的转换（例如 ${\delta }_{ij}=c_1-c_2{S}_{ij}$，其中 $c_1,c_2$ 是实数常数）从相似性中轻松获得非相似性。一种实现正确排序的简单算法是在 ${\delta }_{ij}$ 上进行单调回归，得到与 ${\delta }_{ij}$ 相同顺序的离差 ${\hat{d}}_{ij}$。
$$\sqrt{\frac{{\sum }_{i<j}(d_{ij}-{\hat{d}}_{ij}{)}^2}{{\sum }_{i<j}{d}_{ij}^2}}.$$

通过设置 normalized_stress=True，可以启用规范化的 Stress-1，但它只适用于非度量 MDS 问题，在度量情况下将被忽略。

参考文献：

• “现代多维缩放 - 理论与应用” Borg, I.; Groenen P. Springer 统计学系列 (1997)
• “非度量多维缩放：一种数值方法” Kruskal, J. Psychometrika, 29 (1964)
• “通过优化对非度量假设的拟合度进行多维缩放” Kruskal, J. Psychometrika, 29, (1964)

t-分布随机邻域嵌入 (t-SNE)

t-SNE (TSNE) 将数据点之间的关联转化为概率。原始空间中的关联由高斯联合概率表示，嵌入空间中的关联由学生 t-分布表示。这使得 t-SNE 对局部结构特别敏感，并具有其他一些优势：

• 在单个地图上显示多个尺度的结构
• 显示位于多个不同流形或聚类中的数据
• 减少将点聚集在中心的倾向

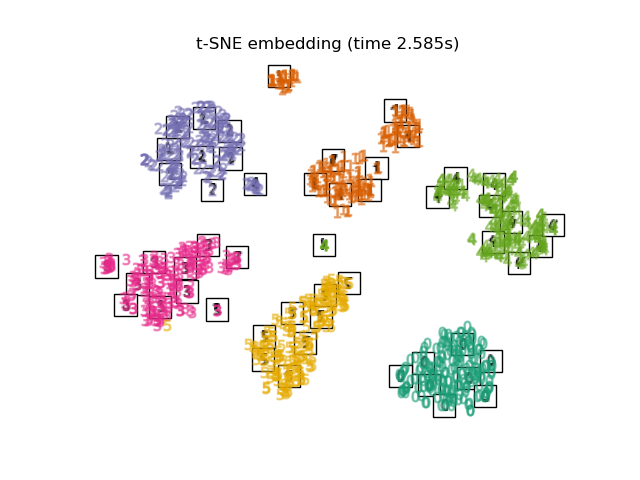
虽然 Isomap、LLE 和其变体最适合展开单个连续的低维流形，但 t-SNE 将专注于数据的局部结构，并倾向于提取聚类的局部样本组，如 S 曲线示例所示。根据局部结构对样本进行分组的能力可能有助于在一个数据集中直观地解开同时包含多个流形的情况，这在数字数据集中是一种常见情况。

通过梯度下降来最小化原始空间和嵌入空间中的联合概率的 Kullback-Leibler (KL) 散度。请注意，KL 散度不是凸的，即使用不同的初始化进行多次重启将导致 KL 散度的局部最小值。因此，有时尝试不同的种子并选择 KL 散度最低的嵌入是有用的。

使用 t-SNE 的缺点大致有：

• t-SNE 的计算成本很高，在包含数百万个样本的数据集上可能需要几个小时，而 PCA 只需要几秒钟或几分钟即可完成
• Barnes-Hut t-SNE 方法仅限于二维或三维嵌入。
• 该算法是随机的，使用不同的种子进行多次重启可能会产生不同的嵌入。然而，选择误差最小的嵌入是完全合理的。
• 全局结构没有被明确保留。通过使用 PCA 初始化点（使用 init=‘pca’），可以缓解这个问题。

优化 t-SNE

t-SNE 的主要目的是可视化高维数据。因此，在将数据嵌入到二维或三维空间时效果最好。

优化 KL 散度有时可能有点棘手。有五个参数控制 t-SNE 的优化，因此可能影响结果嵌入的质量：

• 困惑度 (perplexity)
• 早期夸张因子 (early exaggeration factor)
• 学习率 (learning rate)
• 最大迭代次数 (maximum number of iterations)
• 角度 (exact 方法中不使用)

困惑度被定义为 $k=2^{(S)}$，其中 $S$ 是条件概率分布的香农熵。一个有 $k$ 个面的骰子的困惑度是 $k$，因此 $k$ 实际上是 t-SNE 在生成条件概率时考虑的最近邻居的数量。较大的困惑度会导致更多的最近邻居，并且对小结构不太敏感。相反，较低的困惑度考虑更少的邻居，因此忽略了更多的全局信息，而更关注局部邻域。随着数据集大小的增加，需要更多的点来获得合理的局部邻域样本，因此可能需要更大的困惑度。类似地，噪声较大的数据集将需要较大的困惑度值，以包含足够的局部邻居以看到背景噪声之外的内容。

最大迭代次数通常足够高，不需要任何调整。优化分为两个阶段：早期夸张阶段和最终优化阶段。在早期夸张阶段，原始空间中的联合概率将通过与给定因子的乘法人为增加。较大的因子会导致数据中自然聚类之间的较大间隔。如果因子过高，KL 散度可能会在此阶段增加。通常不需要调整。一个关键参数是学习率。如果学习率过低，梯度下降将陷入一个不良的局部最小值。如果学习率过高，KL 散度将在优化过程中增加。Belkina 等人（2019）建议的一种启发式方法是将学习率设置为样本大小除以早期夸张因子。我们将此启发式方法实现为 learning_rate=‘auto’ 参数。有关更多提示，请参阅 Laurens van der Maaten 的 FAQ（参考文献）。最后一个参数，角度，是性能和准确性之间的权衡。较大的角度意味着我们可以用一个点来近似更大的区域，从而提高速度但减少准确性。

“如何有效使用 t-SNE” 提供了对各种参数影响的良好讨论，以及交互式图表来探索不同参数的影响。

Barnes-Hut t-SNE

这里实现的 Barnes-Hut t-SNE 通常比其他流形学习算法慢得多。优化非常困难，梯度的计算复杂度为 $O[dNlog(N)]$，其中 $d$ 是输出维数，$N$ 是样本数。Barnes-Hut 方法改进了 t-SNE 的精确方法，其中 t-SNE 的复杂度为 $O[d{N}^2]$，但有几个其他显著差异：

• Barnes-Hut 实现仅在目标维度为 3 或更低时有效。构建可视化时通常使用 2D 情况。
• Barnes-Hut 仅适用于稠密输入数据。稀疏数据矩阵只能使用精确方法进行嵌入，或者可以通过稠密低秩投影的近似方法进行嵌入，例如使用 ~sklearn.decomposition.PCA
• Barnes-Hut 是精确方法的近似。该近似由角度参数参数化，因此当 method=“exact” 时，角度参数不使用。
• Barnes-Hut 的可扩展性更强。Barnes-Hut 可用于嵌入数十万个数据点，而精确方法只能处理数千个样本，否则会变得计算不可行。

对于可视化目的（这是 t-SNE 的主要用途），强烈建议使用 Barnes-Hut 方法。精确的 t-SNE 方法对于检查嵌入的理论属性可能是有用的，尤其是在更高维空间中，但由于计算限制，仅限于小型数据集。

还要注意，数字标签大致与 t-SNE 发现的自然分组相匹配，而 PCA 模型的线性 2D 投影产生的表示中，标签区域主要重叠。这是一个强烈的线索，表明这些数据可以通过关注局部结构的非线性方法（例如具有高斯 RBF 核的 SVM）进行良好分离。然而，在 2D 中无法通过 t-SNE 很好地可视化分离均匀标记的组并不一定意味着无法通过监督模型正确分类数据。可能的情况是，2个维度不足以准确表示数据的内部结构。

参考文献：

实际使用技巧

• 确保所有特征使用相同的比例尺。因为流形学习方法基于最近邻搜索，否则算法可能表现不佳。可以使用 StandardScaler 来方便地对异构数据进行缩放。
• 每个算法计算的重构误差可以用来选择最佳的输出维度。对于一个嵌入在 $D$ 维参数空间中的 $d$ 维流形，当 n_components 增加到 n_components == d 时，重构误差会减小。
• 注意，噪声数据可能会“捷径”流形，实质上充当了将本来应该相互分离的流形部分连接起来的桥梁。对于噪声和/或不完整数据的流形学习是一个活跃的研究领域。
• 某些输入配置可能会导致奇异的权重矩阵，例如当数据集中有两个以上的点相同时，或者当数据被分成不相交的组时。在这种情况下，solver='arpack' 将无法找到零空间。解决这个问题的最简单方法是使用 solver='dense'，它可以处理奇异矩阵，但可能会非常慢，具体取决于输入点的数量。另外，可以尝试理解奇异性的来源：如果是由于不相交的集合，增加 n_neighbors 可能有所帮助。如果是由于数据集中存在相同的点，删除这些点可能会有所帮助。

random_trees_embedding 也可以用于推导特征空间的非线性表示，但它不进行降维。