金融欺诈：异常检测技术及最新进展综述Financial Fraud: A Review of Anomaly Detection Techniques and Recent Advances

最新推荐文章于 2024-11-16 17:02:07 发布

数智笔记

最新推荐文章于 2024-11-16 17:02:07 发布

阅读量3.2k

点赞数 9

分类专栏：异常检测文章标签：异常检测深度学习

本文链接：https://blog.csdn.net/wjjc1017/article/details/137460486

版权

异常检测专栏收录该内容

21 篇文章

订阅专栏

论文名称：Financial Fraud: A Review of Anomaly Detection Techniques and Recent Advances

文章信息

关键词:

索引词 - 异常

离群值

异常检测

离群检测

机器学习

深度学习

金融欺诈

信用卡欺诈

保险欺诈

证券和商品欺诈

内幕交易

洗钱

摘要

随着技术的发展和现代社会持续的经济增长，金融行业中的欺诈行为变得更加普遍，每年给机构和消费者造成数百亿美元的损失。欺诈者不断改进他们的手法，以利用当前防范措施的漏洞，其中许多人瞄准了金融领域。这些犯罪行为包括信用卡欺诈、医疗和汽车保险欺诈、洗钱、证券和商品欺诈以及内幕交易。单独使用欺诈预防系统无法提供足够的安全防范来抵御这些犯罪行为。因此，检测系统对于在犯罪行为发生后检测到欺诈行为以及潜在的成本节约更加明显。过去几十年来，研究人员 intensively 研究了用于此目的的异常检测技术，其中许多采用了统计、人工智能和机器学习模型。监督学习算法一直是研究中研究的最流行模型类型。然而，监督学习模型存在许多挑战，这些挑战已经被提出并可以通过最近发表的文献中提出的半监督和无监督学习模型来解决。本调查旨在调查并全面审查应用于检测金融欺诈的最流行和有效的异常检测技术，重点介绍半监督和无监督学习领域的最新进展。

1. 引言

异常检测是一个广泛的领域，解决识别不符合预期行为的数据实例或事件的问题（Chandola, Banerjee, & Kumar, 2009）。异常检测这个术语经常与离群值检测互换使用。许多用于异常检测的技术在根本上是相同的，但根据应用领域的不同会有不同的称呼。异常的其他术语包括不一致的对象、异常、异常、特殊或污染物（Chandola 等，2009; Aggarwal, 2013）。本文选择使用异常检测这个术语；然而，在适当的情况下，也会使用离群值检测，具体取决于问题的处理方式。

识别异常模式或事件的重要性在于它们能够转化为各种应用中的重要、可操作且通常是关键的信息（Chandola 等，2009）。数据中可能存在异常的原因有很多，例如恶意活动或系统故障，但这些原因的共同特点是分析人员感兴趣（Chandola 等，2009）。信用卡数据中的异常行为可能表示身份盗窃或未经授权的一方进行的欺诈交易（Singh & Upadhyaya, 2012）。计算机网络中异常的流量模式可能表明恶意尝试入侵或破坏系统，并导致严重的中断，甚至警示到向未经授权的目的地发送敏感数据的黑客计算机（Chandola 等，2009; Singh & Upadhyaya, 2012）。在医疗领域，异常检测技术可以识别医学图像中的恶性细胞或区域，例如磁共振成像（MRI）扫描（Spence, Parra, & Sajda, 2001; Han, Rundo, Murao, Noguchi, Shimahara, Milacski, & Satoh, 2020）。此外，太空船传感器中的异常测量或读数可能表明故障组件，而在自然界中，地震可以通过在先驱数据中发现异常来预测（Fujimaki, Yairi, & Machida, 2005; Saradjian & Akhoondzadeh, 2011）。在提到的所有应用中，都存在一个数据的“正常”模型，从中异常偏离（Aggarwal, 2013）。

近年来，金融欺诈，包括但不限于信用卡欺诈、保险欺诈、洗钱、医疗欺诈以及证券和商品欺诈，引起了许多人的关注，他们试图阻止这些行为。从经济上看，金融欺诈不断增长的速度引起了严重的担忧。据显示，由于金融欺诈每年造成的全球总损失在数十亿美元范围内，有些数据表明美国每年的损失超过 4000 亿美元（Bhattacharyya, Jha, Tharakunnel, & Westland, 2011; Kirkos, Spathis, & Manolopoulos, 2007）。与金融欺诈相关的犯罪类型还对行业产生了更广泛的影响，并与资助非法活动，如有组织犯罪和贩毒有关（West & Bhattacharya, 2016）。这些犯罪行为所造成的损失通常由公司和商家承担，他们往往需要承担欺诈行为造成的所有费用。例如，对于信用卡欺诈，商家需要承担退款、行政成本，以及那些被这些行为害的消费者失去信心的损失（Quah & Sriganesh, 2008; Sánchez, Vila, Cerda, & Serrano, 2009）。因此，这些类型的欺诈行为的后果是严重的，开发检测它们的策略和技术的重要性显而易见。

本文的目的是回顾并提供对金融欺诈中应用的异常检测技术的当前研究和文献的全面和结构化概述。通过清晰讨论各种研究方向和开发的技术，旨在提供该领域最新贡献、进展和实验结果的完整指南。

我们将论文组织如下：第二部分介绍了相关领域的调查概述。这一概述的动机在于显示过去的调查论文往往保持相当狭窄的范围，因此强调了金融欺诈领域需要一个集中的信息源。本文的第三部分定义了异常，详细概述了相关检测任务，并概述了问题的性质及其相关挑战。在第四部分，对金融领域的欺诈背景信息进行了情境化，概述了不同类型的欺诈行为以及它们发生的见解。在第五部分，提供了对应用于检测金融欺诈的异常检测技术的调查文献的详细回顾，总结了已发表研究的主要发现、局限性和建议。我们在第六部分对主要发现进行最终评论，并提出未来研究方向的建议。

2. 相关调查

大量已发表的研究文献研究了在各种应用中应用异常检测技术，这已成为近年来许多调查和综述论文的焦点。其中一些调查主要关注对各个领域的应用、策略和技术进行广泛范围的研究，对进一步研究产生了重要影响。

Hodge 和 Austin 在 2004 年发表了关于异常或离群值检测方法的一篇最早的调查之一，全面回顾了这一主题（Hodge & Austin, 2004）。该文献提供了有关离群值或异常以及检测它们所面临的挑战的广泛背景，以及应用于该任务的早期统计、机器学习和集成方法的彻底回顾。2009 年，Chandola 等人也调查了研究中提出的各种异常检测技术，这些技术之前未被 Hodge 和 Austin 涵盖，提供了更多关于它们在各种现实应用中的见解（Chandola 等，2009）。2012 年，Zimek 等人发表的一篇调查专门回顾了针对高维数值数据的无监督异常检测技术，详细讨论了“维度灾难”的各个方面（Zimek, Schubert, & Kriegel, 2012）。文献涉及了两类专门算法的比较：一类处理无关特征或属性的存在，另一类更关注效率和有效性问题（Zimek 等，2012）。时间数据对异常检测构成另一个问题，这是 Gupta 等人在 2014 年进行了广泛调查的问题（Gupta, Gao, Aggarwal, & Han, 2014）。随着计算能力的提升，各种形式的时间数据变得可用，作者广泛审查了已为时间序列数据启用的异常检测技术（Gupta 等，2014）。作者深入探讨了时间异常检测的各种应用以及每个领域中相关挑战。
Ngai等人在2011年提出了一份更具方法论性的文献综述，涉及了金融欺诈检测领域的现有文献（Ngai, Hu, Wong, Chen, & Sun, 2011）。根据一个用于分类论文的概念框架，根据其应用和技术，演示了对洗钱、抵押和证券商品欺诈研究的缺乏和需求（Ngai等人，2011）。West和Bhattacharya在2016年对Ngai等人先前提出的框架进行了扩展，通过进一步对调查文献中提出的方法进行分类，基于它们的性能（West & Bhattacharya, 2016）。研究论文是根据其方法论中所概述的技术的准确性、召回率和特异性进行比较和组织的，采用了比以往更定量的方法。

Pourhabibi等人（Pourhabibi, Ong, Kam, & Boo, 2020）在2020年提出了一份关于不同基于图的异常检测技术的系统文献综述，这些技术已在金融欺诈背景下的已发表文献中进行了研究。作者们广泛调查了提出的方法，以分析通信网络中的连接模式，以识别可疑行为（Pourhabibi等人，2020）。该综述的框架与Ngai等人在2011年的调查非常相似，涵盖了不同技术的相关限制，并提供了对四种基于图的方法的概述：基于社区、基于概率、基于结构、基于压缩和基于分解（Pourhabibi等人，2020）。这些方法的应用包括银行欺诈检测、保险欺诈检测、反洗钱等。对每种技术的亮点和面临的挑战进行了讨论，作者进行了深入分析。根据调查论文中的调查和分析，作者从学术论文中识别的差距提出了未来研究工作的方向。

近年来，大部分关于金融欺诈检测的研究工作集中在信用卡欺诈检测技术上，这一点从相关文献的丰富程度就可以看出，远远超过其他金融欺诈类型的研究。因此，在过去十年中，许多综述论文评估了检测信用卡欺诈研究现状。Delamaire等人是最早在2009年审查这一特定主题的学者之一，在他们的工作中，确定了不同类型的信用卡欺诈以及用于检测它们的技术（Delamaire, Abdou, & Pointon, 2000）。作者们对信用卡欺诈中的标准术语、领域中的关键统计数据和数字提供了全面的背景。他们还展示了已发表文献的研究结果，并进行了比较和分析，讨论了可以根据所面临欺诈类型采取的各种措施。此外，文献中还提出了关于伦理问题的讨论，即由于将真实交易误分类为欺诈交易所引起的伦理问题，以及将欺诈交易误分类为真实交易所产生的成本（Delamaire等人，2000）。

2012年，Zareapoor等人进行了一项调查，重点关注了用于信用卡欺诈检测的特定统计和机器学习技术（Zareapoor, 2012）。文献中对每种技术的历史背景进行了介绍，并对它们在信用卡欺诈检测系统中的工作或操作进行了高层次的概述。尽管作者对所述技术的性能进行了相互比较的评论，但我们发现这项工作存在一个重大缺点：即缺乏对作者在（Zareapoor, 2012）中审查的文献产生的可量化性能指标的讨论。2017年由Adewumi和Akinyelu发表的文献部分地解决了前述工作中的差距，简要讨论了所涵盖技术的分类准确性（Adewumi & Akinyelu, 2018）。作者还讨论了一些限制，如数据的高维度、不平衡数据集及其对所审查研究性能的影响。最后，文献确定了一种使用人工生成数据来克服信用卡检测系统某些限制的发展趋势，并建议进一步探索这种方法可能是有前途的。

大多数现有综述提供了对金融欺诈检测中应用的技术的非常一般性的概述；然而，许多综述并未充分突出已发表研究所面临的挑战和问题。另一个重要问题是缺乏讨论关于所审查方法中采用的性能指标的具体细节，许多综述只对不同技术进行定性比较。大多数综述论文中也观察到了缺乏结构，其中许多综述未提供足够的背景知识，以便进一步理解相关方面。尽管在该领域的现有综述论文中存在不同的缺陷，但每篇综述在各个方面都具有不同的优势，为任何读者提供了价值。

在本次调查中，我们通过涵盖最近几年应用于检测各种金融欺诈类型的最新技术，扩展了先前作者的工作。我们希望解决以往综述的各个缺点，以提供更全面、详细和完整的综述。我们将通过定义异常的概念，并对各种异常和不同领域中异常检测任务所面临的一般挑战进行全面的背景和讨论。描述和概述了异常检测模型或方法使用的不同类型的学习，以及用于评估它们的各种性能指标。我们还定义了金融欺诈，概述了其历史以及属于该分类的各种欺诈行为。详细介绍了与金融欺诈损失相关的数据和统计数字，以证明使用异常检测技术来检测欺诈金融活动的必要性。还总结了不同类型的欺诈，突出展示了它们是如何实施的以及目前已经采取的措施来防范。最重要的是，我们对金融欺诈检测的研究文献进行了批判性审查，重点关注了2002年至2020年发表的论文。我们强调评估和比较所使用的方法的限制、挑战和整个性能指标范围，以对当前最新研究成果提供知情评论。

从调查文献中涵盖的技术涵盖了深入研究的模型，如支持向量机（SVM）、决策树（DT）、随机森林（RF）、隐马尔可夫模型（HMM）、多层感知器网络（MLP）等。与其他综述不同的是，我们涵盖了使用以前未研究过的模型来检测金融欺诈的新颖研究论文。其中最突出的是深度学习架构，如卷积神经网络（CNN）、自动编码器（AE）和生成对抗网络（GAN）。最后，我们总结了本次综述的主要发现，并提出了未来研究工作的方向建议。

3. 问题描述与制定

3.1. 什么是异常？

许多作者提出了关于异常的不同定义；然而，并没有一个被普遍采用的定义。关于异常的确切定义取决于对数据结构和所考虑应用的假设。然而，存在一些被认为适用于大多数情况，无论设置或应用的定义。在这些定义中，最广泛认可的是Hawkins的定义，他如下定义了异常或者在这种情况下的异常值的概念：“异常值是指偏离其他观测值如此之远，以至于引起怀疑它是由不同机制生成的观测值”（Hawkins, 1980）。这个定义是基于统计学直觉的数据，其中正常数据遵循一个生成机制，而异常值是偏离这个机制的样本或实例。因此，异常通常传达了关于影响生成机制的系统异常特征的有用信息（Aggarwal, 2013）。在本文的其余部分，我们采用Hawkins对异常概念的定义。

图1展示了不同类型异常的概念的二维图。从这个图中可以看出，数据元素形成了两个正常区域，分别表示为 $N_{1}$ 和 $N_{2}$ ，这些区域是大多数事件所在的区域。远离大多数其他观测值的观测值，无论是单独的还是作为一个小集体，如点 $o_{1}$ 、 $O_{2}$ 和区域 $O_{3}$ ，都是异常值。

图1. 在简单的二维表示中展示异常数据的图形化可视化。
异常情况发生的原因有很多，比如人为错误、仪器故障、人口中的自然偏差、欺诈活动、系统行为变化或系统内部的故障（Hodge & Austin, 2004）。异常检测系统如何处理异常取决于应用领域。例如，假设异常表明数据输入员输入了一个打字错误，那么简单地通知数据输入员更正错误就可以帮助恢复异常数据为正常输入。一旦识别出仪器读数中的异常数据，就可以简单地删除它们。此外，在入侵监控或欺诈检测等关键环境中，异常检测系统必须能够立即和实时地检测异常，并发出适当的警报以便干预（Hodge & Austin, 2004）。

3.2. 异常类型

异常可以分为三种不同的类别，而正在处理的异常类型是任何异常检测技术考虑的关键方面。

点异常是最简单的异常类型，也是大多数应用异常检测技术研究的重点。它们被定义为与其余数据显著不同的单个数据实例或事件。一般来说，它们是不在已建立的正常或分隔边界内的点，比如在中的点 $o_{1}$ 和 $o_{2}$ 。举个现实生活中的例子，考虑个人的信用卡使用数据，仅定义了一个特征：购买金额。当进行比较时，任何大于该个人正常消费范围的交易都会被视为点异常。

上下文异常是在特定上下文中异常的数据实例，如果在其他情况下则不是异常。数据集结构为这类异常引入了上下文的概念，问题的制定严格要求其规范。每个数据实例都使用两个属性来定义，即上下文属性和行为属性。上下文属性确定该实例的上下文，比如时间序列数据中的时间。行为属性定义了非上下文特征，比如信用卡数据集中的购买金额。异常行为反过来是在特定上下文中使用行为属性确定的。例如，在信用卡欺诈中，上下文属性可能是购买时间。假设一个人每周的消费账单是一百美元，除了圣诞节那周是一千美元。在五月份的一个普通周购买一千美元将被视为上下文异常，因为它不符合时间上下文中的典型行为，尽管在圣诞节周花同样的金额则被视为正常（Chandola 等，2009）。

最后，集体异常是与整个数据集相关的一组相关实例，这些实例在整个数据集中是异常的。集体异常中的个别事件或数据实例本身不一定是异常的；然而，它们作为一个集合的出现是异常的。需要注意的是，点异常可以出现在任何数据集中，而集体异常只能出现在数据集中存在数据实例之间关系的情况下。当数据中存在上下文属性时，上下文异常才可能出现。如果在特定上下文中观察到点异常或集体异常，它们甚至可以成为上下文异常（Chandola 等，2009）。

3.3. 异常检测中的挑战

如前所述，异常是不符合预期正常行为的观察或事件。因此，一种直观的方法是定义一个区域来代表正常行为，使得不在正常区域边界内的观察被标记为异常，如图1所示的例子。然而，由于异常检测问题的独特性质，这种看似简单的方法变得更加具有挑战性，这些挑战与大多数分析和学习问题有着不同的复杂性。这些复杂性归因于几个因素。

很难定义一个能够涵盖所有正常行为可能性的正常区域或边界，通常正常和异常行为之间的边界缺乏精确性。由此导致的结果是，靠近边界的正常或异常类的观察可能被错误分类。此外，由于恶意活动引起的异常通常是不断变化和适应的，受到异常检测系统对手及其试图将异常事件伪装成正常事件的影响，最终增加了检测的难度。一般来说，在其他领域中，正常行为不断演变，现在的正常行为可能无法充分代表未来行为。概念漂移是大多数文献用来指代随时间变化的基础模型的现象（Gama, Žliobaite, Pechenizkiy, & Bouchachia, 2014）。异常也是异质的，意味着它们是不规则的，即一个异常类可能表现出与另一个异常类完全不同的异常特征（Pang, Shen, Cao, & van den Hengel, 2020）。

此外，异常检测中异常的概念因不同领域和应用而异。在医学领域，与基线略有偏差（如体温波动）可能被视为异常。相比之下，在金融领域，特别是在股票市场中，相似程度的偏差可能被视为正常（Chandola 等，2009）。因此，将为一个领域开发的技术应用于另一个领域可能并不那么直接。

影响异常检测复杂性的另一个因素是缺乏用于训练和验证模型的标记数据，原因有几个。处理敏感数据时存在隐私问题，或者如果必须由人类执行标记数据，则标记数据的成本较高（Domingues, Filippone, Michiardi, & Zouaoui, 2018）。异常实例的发生也很少，与通常占绝大多数数据的正常实例形成对比（Pang 等，2020；Boukerche, Zheng, & Alfandi, 2020）。在这种情况下，标准分类器异常检测技术往往会忽略小类别，因为它们被大类别所淹没（Chawla, Japkowicz, & Kotcz, 2004）。在正常数据实例中，噪声的存在，通常类似于异常，也增加了一个挑战，使得在数据集中更难推断出清晰的边界或决策规则。

在低维空间中，异常通常显示出明显的异常特征。然而，在高维空间中，它们变得隐藏且难以识别，这是一个长期存在且广泛研究的问题，被称为维度灾难（Zimek 等，2012）。一个简单的解决方案是将数据的维度降低到由原始特征的较小子集或新构建的特征跨越的较低空间，比如在子空间和基于特征选择的方法中（Keller, Muller, & Bohm, 2012；Lazarevic & Kumar, 2005）。在高维数据中识别复杂的特征交互仍然是异常检测的一个重要挑战。此外，在新特征空间中保证信息保留对于准确的下游异常检测至关重要。然而，由于异常的异质性，这一点变得更加困难（Pang 等，2020）。

异常检测技术能否应用于一个问题也受到输入数据中特征值性质的影响。当使用不同的统计或机器学习技术时，数值和分类或符号数据需要不同的统计模型。在某些情况下，可能需要通过使用各种技术将符号数据转换或编码为数值数据。在使用基于距离的技术时，根据输入的性质需要不同的距离度量。有些技术只能处理图像数据，通常以实数矩阵展平为向量表示。数据实例之间甚至可能存在关系，比如在空间、时间和图数据中。这是在设计阶段必须考虑的另一个因素，以确保所使用的技术对于特定应用的适用性、稳健性和性能。

3.4. 数据标签和输出

在任何数据集中，与数据实例相关联的标签表示该实例是异常还是正常。然而，需要注意的是，获取准确标记的数据，代表所有类型行为的数据，通常是具有挑战性和成本高昂的。标记数据需要大量时间和精力，因为通常是由应用领域的专家手动完成的（Chandola 等，2009；Aggarwal, 2013）。此外，相比获取标记的正常行为，获取涵盖所有可能异常行为类型的标记数据要困难得多。由于异常的动态性，如异常检测中所描述的挑战，异常行为可能会发生变化，导致新的异常，而这些异常可能没有任何标记数据。

在决定使用何种异常检测方法时，标记数据的可用性是一个重要考虑因素。一个方法可以被归类为有监督、半监督或无监督异常检测的三个类别。
半监督异常检测技术假设数据集中仅有标记的实例属于正常类别。因此，这些技术更具适用性。与监督异常检测不同，模型仅针对正常类别构建，而不是异常类别。然后，将数据的测试集与模型进行比较，以识别异常实例。这在某些情况下非常有用，比如对于难以建模的异常，比如大型车辆（如飞机和航天器）中的故障（Fujimaki, Yairi, & Machida, 2005）。针对仅有异常类别可用的数据集设计的技术和文献范围非常有限，因为很难获取代表所有异常行为的数据。

无监督异常检测是三类中最广泛适用的，因为这些技术不需要数据集中的任何标签。无监督方法做出的一个隐含假设是，在数据的测试集中，异常事件远不如正常事件频繁；否则，这些技术的误报率将高于预期。通常会将半监督方法调整为无监督异常检测问题，使用数据的训练集的未标记样本。在这种情况下，需要做一个假设：测试集中有很少的异常实例，并且所学习的模型对这些少数异常实例具有鲁棒性。

看起来，异常检测技术的输出可以是每个实例的正常或异常标签。然而，存在评分技术，涉及为每个实例分配一个分数，该分数对应于异常程度，以生成异常分数的有序列表。然后可以考虑一些最高分数，如果已知异常实例的比率，或者分配一个截断分数，如特定应用的阈值，以将最相关的实例标记为异常。二元分类技术不能直接提供相同的灵活性；然而，每种技术的参数选择都允许间接控制。

3.5. 性能度量

异常检测问题通常被视为分类任务，但不是唯一的。评估分类模型性能的一种有效方法是检查其混淆矩阵。混淆矩阵描述了数据集的真实情况与模型预测之间的差异。还有其他更简洁的指标，可以提供有关分类器性能的更具体信息。精确度是正面预测的准确性。分类器的召回率，也称为灵敏度，是分类器正确检测的正实例比例。准确率是模型进行的所有正确预测的数量。分类器的特异性是正确分类的负样本与负样本总数之比。尽管直观上可能会尝试最大化召回率和精确度，但两个值之间存在反向关系。强制提高精确度可能导致召回率降低，反之亦然。这被称为精确度/召回率折衷。而更好的最大化度量是 F-分数（也称为 $\mathrm{F}_{1}$ -分数），它是精确度和召回率的调和平均值。

通过调整分类器的决策阈值，可以监控性能变化，以在召回率和精确度等特定指标之间进行权衡。这被称为参数评估，它评估了通过改变决策阈值产生的所有可能混淆矩阵。然后绘制两条曲线，即受试者工作特征（ROC）曲线和精确度-召回率曲线（Lucas & Jurgovsky, 2020）。通过测量 ROC 曲线下的面积（AUC）来比较分类器，完美的分类器的 AUC 等于 1，纯随机分类器的 AUC 等于 0.5。两个轴都与它们代表的类成比例，因此 ROC 曲线不受不平衡数据集的影响（Lucas & Jurgovsky, 2020）。精确度-召回率曲线（PRC）将精确度绘制在 y 轴上，将召回率绘制在 x 轴上。召回率是正类的比例，表示识别的正类的比例。精确度基于正类和负类。因此，不平衡的数据集通过使分类更具挑战性来影响精确度。类似地，可以确定精确度-召回率曲线下的面积（AUPRC）以比较不同分类器的性能。

尽管上述性能度量是评估分类器最常用和最受欢迎的方法，但还有许多其他方法，这里讨论的指标列表并不详尽。基于相关特征将相似数据点分组的聚类算法使用各种距离度量，如均方误差（MSE）、欧氏距离、曼哈顿距离等，来量化样本或观察之间的相似性或差异。这些无监督技术将数据集分成有意义的子集或组，其中组内实体相似，不同组的实体不同（Sabau, 2012）。

4. 金融欺诈

由于未检测到的异常可能对行业和日常生活产生潜在后果，金融欺诈在过去十年中引起了更多关注。这些犯罪的性质各异，可能导致不稳定的经济、增加生活成本并影响消费者的安全感（Syeda, Zhang, & Pan, 2002）。金融欺诈没有被普遍接受的定义；然而，我们采用了注册欺诈审计师协会（ACFE）的定义，即“通过狡诈、欺骗或其他不公平手段故意剥夺他人财产或金钱”的定义（注册欺诈审计师协会, 2004）。

随着互联网、硬件设备（如手机和笔记本电脑）和社交媒体等现代技术的迅速扩张和进步，欺诈活动也在增加（Kou, Lu, Sirwongwattana, & Huang, 2004）。这导致企业损失数十亿美元，因此对探索用于欺诈检测的异常检测技术进行了大量努力。能够在欺诈发生时迅速识别欺诈是至关重要的，因为未检测到的案例会随着时间而产生成本（注册欺诈审计师协会, 2020）。不仅是个人欺诈者和犯罪者利用了技术的进步。发达的有组织的犯罪者和犯罪团体也一直在投资于扩大和改进他们的技术（Bhattacharyya 等, 2011）。因此，不断发展和改进这些欺诈检测技术至关重要，因为欺诈者始终在适应和创新策略和方法以规避它们（West & Bhattacharya, 2016）。

据互联网犯罪投诉中心（IC3）报告，在美国报告了 467,361 宗互联网犯罪投诉，报告的损失超过 35 亿美元，比前一年增长近 30%（中心, 2019）。这些损失涉及各种行为，如篡改商业电子邮件以进行未经授权的资金转移、涉及欺诈支票和信用卡申请的身份欺诈案等。根据注册欺诈审计师协会 2020 年的《全球国家报告》，全球组织每年损失的收入占 5%，典型的欺诈案件被未发现长达 14 个月，每月平均损失 8,300 美元（注册欺诈审计师协会, 2020）。表 1 展示了 IC3 从 2015 年到 2019 年每年报告的投诉和总损失。从表 1 可以明显看出，自 2017 年以来，报告的总损失每年都在加速增长，这进一步突显了欺诈活动在适应和演变以规避现有系统的过程中持续存在。

金融欺诈已被联邦调查局（FBI）分类。这些犯罪的特征是欺诈、隐瞒或违反信任，无论是否伴随暴力威胁或实际暴力（局, 2011）。在该分类下存在各种类型的欺诈；其中一个例子是银行欺诈，包括信用卡欺诈、洗钱和抵押欺诈。保险欺诈是另一种常见的金融欺诈类型，涉及各种索赔，包括作物、医疗保健、汽车等。还有其他类型的金融欺诈，如证券和商品欺诈以及内幕交易。然而，在本调查中，我们主要关注将异常检测技术应用于信用卡和借记卡欺诈，以及保险欺诈。调查还涵盖了少数几篇涉及反洗钱研究的最新进展。我们注意到，关于其他类型的金融欺诈，如抵押欺诈、商品和证券欺诈以及内幕交易，可用的研究文献较少。因此，这些欺诈类型超出了本调查论文的范围。

表 1

IC3 每年收到的投诉和报告的总损失（中心, 2019）。

年份	收到的投诉	总损失（美元）
2015	288,012	1,070,700,000 美元
2016	298,728	1,450,700,000 美元
2017	301,580	1,418,700,000 美元
2019	467,361	35亿美元

4.1. 信用卡欺诈

信用卡作为主要交易方式的广泛使用是过去几十年来日常生活和社会数字化的显著例证。这种普及也带来了信用卡欺诈问题，涉及使用复杂的策略和技术来窃取资金和财产。根据（报告，2020），2020年信用卡交易的欺诈损失达到286.5亿美元，其中美国占了这一总损失的三分之一，达到96.2亿美元。随着信用卡的普及和使用越来越普遍，人们也担心欺诈行为的增加。未被发现的信用卡欺诈行为会带来重大后果，因为这些犯罪甚至被用于资助有组织犯罪、贩毒甚至资助恐怖分子。

信用卡欺诈可分为申请欺诈和行为欺诈两种，有时也被称为离线和在线欺诈（Kou, Lu, Sirwongwattana, & Huang, 2004; Bolton & Hand, 2001）。申请欺诈通常涉及身份欺诈，因为欺诈者通常会试图使用他人的个人信息向信用公司申请新卡。行为欺诈包括四种不同的行为，包括邮件盗窃、遗失或被盗的卡、伪造卡、“持卡人不在场”欺诈或破产欺诈。邮件盗窃欺诈主要涉及欺诈者截取他人的邮件以获取实体信用卡或个人银行信息，然后用这些信息进行申请欺诈。遗失或被盗的信用卡相关欺诈通常发生在欺诈者偷走个人实体卡，无论被盗者是否知情，或者欺诈者找到或获取遗失的卡时。破产欺诈被认为是最难以检测的欺诈类型之一，通常涉及人们使用信用卡而没有任何还款意图，然后申请个人破产，由Ghosh和Reilly在1994年定义。

随着日常生活的快速数字化，更多的信息在线上可获得，随之也更容易受到犯罪分子和欺诈者的攻击或利用。欺诈者依赖这些漏洞通过非法手段获取信用卡信息，然后将其用于制作假卡或伪造卡。所有提到的方法也可能涉及“持卡人不在场”欺诈，这只需要信用卡详细信息即可远程进行交易，例如通过邮件、电话或互联网。获取用于实施这些类型欺诈行为所需信息的方式有很多，比如在线“钓鱼”诈骗欺诈不知情的个人，或通过入侵公司网络和计算机系统，甚至通过安装在篡改的ATM卡读取器上的物理设备，称为“窃取器”来窃取人们的卡信息。

Bolton和Hand指出，在早期的信用卡欺诈检测研究中存在着发表文献的匮乏，这归因于两个原因。首先，欺诈检测中的思想交流通常非常有限，因为详细描述检测技术可能会违反直觉，这可能会为设计新工具和技术绕过这些检测技术提供所需的知识和信息。其次，他们还指出，这些类型欺诈数据集通常是保密的，很少公开，即使在极少数情况下公开也会进行审查。正如前面讨论的，随着时间的推移，未被发现的欺诈也会带来成本，这意味着欺诈检测的价值是时间的函数。欺诈活动被尽早发现，个人和公司的潜在损失就越小。这一点尤为重要，因为典型的欺诈者已被发现会通过尽可能短的时间尽可能多地消费，直到欺诈被发现并且卡被停用。

大多数信用卡欺诈检测策略涉及通过分析个人的消费行为和模式来创建持卡人的概要（Abdallah, Maarof, & Zainal, 2016）。Chandola等人将基于概要的方法分类为“按持卡人”方法或“按操作”方法。按持卡人方法根据每位信用卡用户的使用和消费历史对其进行概要，将新交易与用户的概要进行比较，并将与概要不一致的交易标记为异常。

这种方法的缺点在于通常成本较高，因为它需要一个中央数据存储库，每次用户进行交易时都必须查询该存储库。按操作方法从发生在特定地理位置的交易中检测欺诈交易，这些地理位置不太可能被真实持卡人频繁访问。这两种方法检测到的异常类型都是上下文异常，其中“按持卡人”方法的上下文是用户，“按操作”方法的上下文是地理位置。在使用信用卡数据集构建欺诈检测系统或模型时，交易样本由描述或描绘每个样本信息的初始一组原始特征描述。从调查的文献中可以看出，尽管研究不同，但描述数据集的原始特征通常非常相似。经调查发现，这是由国际金融报告准则基金会设定的标准造成的，该基金会管理和监管信用卡发行机构和金融机构必须遵守的财务报告实践。本文调查的文献中使用的大多数数据集中常见的原始特征总结如下表所示。

4.2. 保险欺诈

保险欺诈是另一种涉及索赔过程中索赔人、医疗保健提供者、保险公司员工甚至代理人和经纪人进行某种欺诈或欺骗的金融欺诈类型。受欺诈保险索赔影响最大的行业是医疗保险和汽车保险行业；然而，作物和家庭保险欺诈也存在，尽管缺乏相关文献。据估计，美国每年的保险欺诈总成本超过800亿美元，最终以更高的保险费形式转嫁给消费者。

表2

信用卡数据集中典型原始特征摘要（Bahnsen等，2016）。

特征	描述
交易ID	交易识别号
时间	交易日期和时间
账户号码	客户的身份证号码
卡号	卡的识别号
交易类型	网络、ATM或POS
输入模式	芯片和密码或磁条
金额	交易金额
商家代码	商家类型的识别
商家组	商家组识别
国家	交易国家
国家2	居住国家
卡类型	Visa借记卡、万事达卡、美国运通
性别	持卡人性别
年龄	持卡人年龄
银行	发卡银行

在这一类别中，各种不同类型的欺诈中，汽车保险欺诈检测引起了最多关注。根据国际会计组织KPMG代表加拿大保险局进行的一项研究，2012年加拿大安大略省汽车保险欺诈索赔的成本超过16亿美元。此外，据报道，在汽车保险索赔中，有21%到36%的案件涉嫌欺诈，而涉嫌欺诈的案件中不到3%最终被起诉。

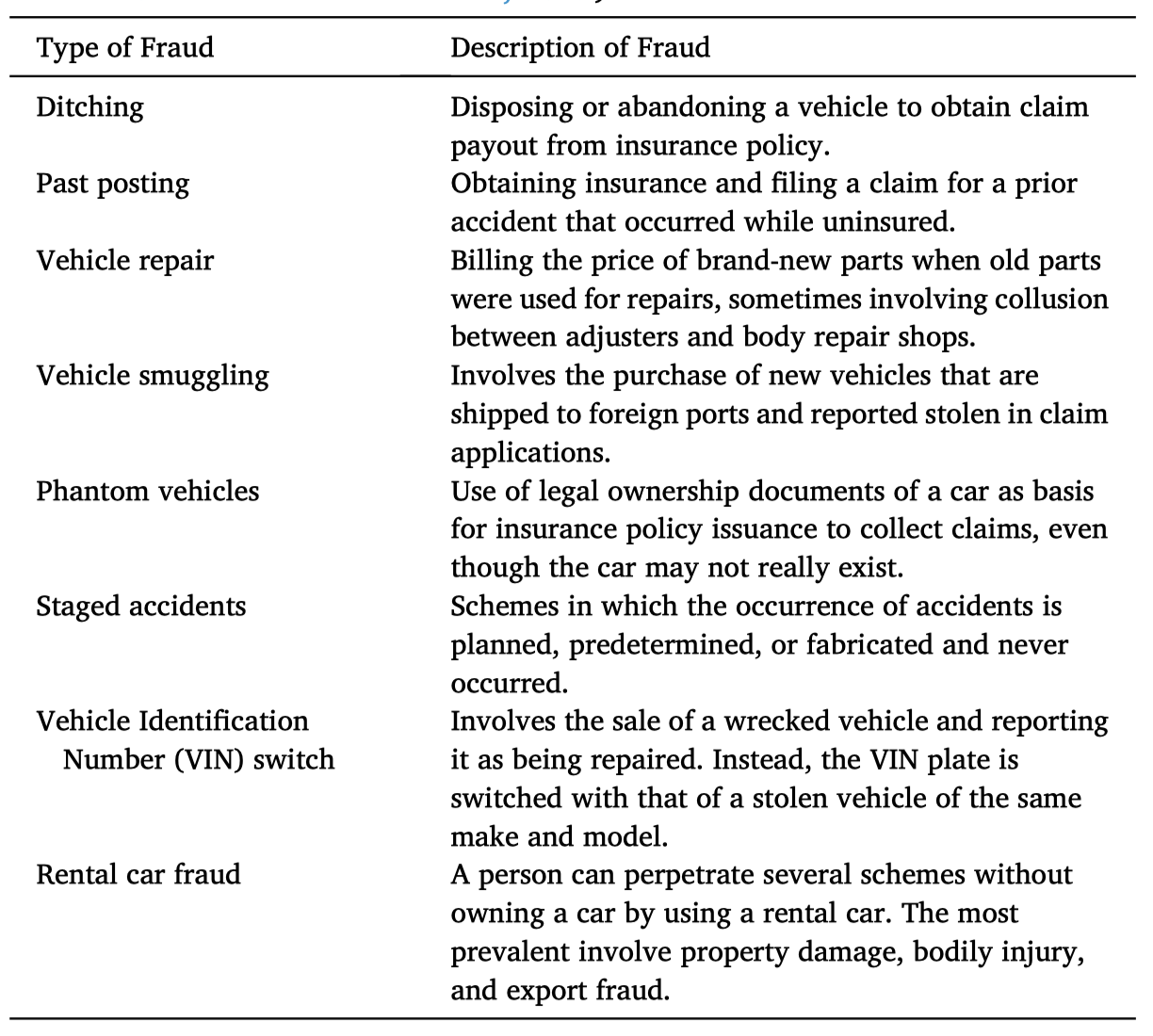
汽车保险索赔通常涉及保险公司与被保险个人或组织之间的合同，以覆盖车辆的盗窃或意外损坏相关费用。欺诈索赔可以由个人欺诈者实施；其中一种方式是在索赔过程中进行欺骗。还有证据表明，有组织团体合作进行保险欺诈，通常是通过制造或伪造事故，有时甚至可能根本没有发生事故；相反，车辆被运到事故现场。无论如何，大多数欺诈案件都是机会主义欺诈，因为它们并非计划好的，而是个人利用事故带来的机会夸大损失或索赔陈述。汽车保险欺诈中涉及的一些方案已被ACFE识别和定义，其中最常见的方案描述在表3中。

表3

不同类型的汽车保险欺诈计划描述（注册会计师欺诈检查员协会，2019）。

对于医疗保健（Yang & Hwang, 2006）。根据国家医疗保健反欺诈协会（NHCAA）的报告，美国2018年因医疗保健保险欺诈索赔造成的总损失保守估计超过1000亿美元，约占当年医疗保健总支出的3%，即3.6万亿美元（协会，2018）。然而，一些政府和执法机构估计损失可能高达3600亿美元。斯帕罗（Sparrow, 2000）是最早将医疗保健保险欺诈者行为分类为“打一枪就跑”或“一直偷一点”的人之一。对于“打一枪就跑”的欺诈者，他们会尽可能提交多个欺诈索赔，然后在收到支付后不久消失。而“一直偷一点”的欺诈者则试图确保他们的行为不被发现，以便能够长时间持续地进行欺诈索赔或计费。FBI（局，2011）在表4中概述和描述了用于欺诈医疗保险政策的各种欺诈活动。

传统上，检测欺诈保险索赔主要依赖于领域专家进行手动审计和检查，这可能既昂贵又低效，特别是这些类型的索赔必须在支付之前被检测出来。由于这种时间敏感性，近年来，机器学习和数据挖掘领域的技术在检测保险欺诈方面的应用得到了越来越多的关注和认可。随着计算能力和算力的不断研究和发展，这些技术表现出在较短时间内检测欺诈案例的潜力，可能比手动检查更准确，进而导致显著减少财务损失。这最终转化为成本的降低和整体潜在利润的增加。

4.3. 洗钱

犯罪分子或恐怖分子个人和组织用来合法化或“洗净”其犯罪所得并掩盖其来源的过程被称为洗钱。这些犯罪行为通常与有组织犯罪团伙、毒品走私、性交易以及资助恐怖分子有关（West & Bhattacharya, 2016）。洗钱是一个全球性问题，对世界经济造成巨大成本，因其对国家经济的破坏性影响。此外，洗钱还可能危及金融机构的稳定性，并增加其运营风险，因为洗钱往往会激励和助长公共和私营部门的腐败（Schott, 2004）。这使得那些充斥着洗钱和腐败的国家对外国投资者不那么具吸引力，从而加剧了其公民面临的不平等现象（Schott, 2004）。

表4

不同类型的医疗保险欺诈计划描述（局，2011）。

欺诈类型	欺诈描述
为未提供的服务计费	涉及提供者为未提供或先前索赔的服务计费。
服务编码升级	提供者提交报销价值大于提供服务价值的索赔的做法。
物品编码升级	提供者的计费做法，其中索赔的物品价值大于实际提供的物品价值。
重复索赔	为同一事物提交多个索赔，更改部分索赔，如日期等。
拆分计费	将账单分段提交以最大化可能已以较低成本一起计费的服务的报销价值。
过度服务	提供的医疗服务或物品超出患者实际需求
医疗无必要服务	不符合患者医疗状况或诊断的服务。
回扣	为了转诊患者接受医疗服务或物品而提供、索取或接受金钱或其他有价物品。

洗钱活动的行为模式和结构网络特征对反洗钱研究至关重要。然而，传统研究主要集中在立法考虑和合规要求上，并在方法上受限于事件识别、避免检测和怀疑监视（Gao & Ye, 2007）。因此，调查通常是手动进行的，这既耗时又资源密集，乏味。因此，应用异常检测技术可能减少处理这些犯罪所涉及的大量数据集的时间，并甚至导致检测效果的提高和减少误报率（Gao & Ye, 2007）。然而，我们注意到，在已发表的文献中，对将异常检测技术应用于反洗钱的研究文献普遍缺乏。

4.4. 其他类型的欺诈

金融领域遇到的另一种欺诈类型是证券与商品欺诈。这种类型的欺诈可能涉及各种不同的计划，FBI将其中一些描述为金字塔计划、庞氏计划、优质银行计划、高收益投资欺诈、预付费欺诈、对冲基金欺诈、商品欺诈、外汇欺诈、市场操纵、经纪人侵占和尾盘交易（局，2011）。随着资本市场的不断整合，企业筹集或获取资本以及投资者实现投资组合多样化的机会前所未有地增加。随之而来的机会增加也带来了相应的欺诈风险上升，因此需要进行研究以检测这些类型的欺诈。

FBI将抵押欺诈定义为借款人在任何过程中对信息进行实质性虚假陈述、误导或遗漏，而这些信息被核保人或贷款人依赖以获得贷款（局，2011）。此外，公司欺诈涉及对财务信息的伪造、公司内部人员的自私交易或阻碍司法公正，旨在掩盖这些犯罪行为的任何一种。最后，大众营销欺诈是一种利用大众传播媒体的犯罪的通用术语（局，2011）。

5. 用于欺诈的异常检测

异常检测在金融欺诈检测中起着重要作用，并用于从大量数据中识别和提取信息（Ngai等，2011）。已经有大量文献应用统计方法以及人工智能和机器学习技术来处理信用卡和保险欺诈检测，其中大多数集中在后两者上。此外，大多数研究论文已经开始将重点转向无监督技术，其中许多技术解决了数据不平衡和缺乏可用数据的问题。

信用卡欺诈经常使用的模型有决策树（DT）、支持向量机（SVM）、逻辑回归（LR）、k均值聚类、k最近邻（kNN）等（Sahin & Duman, 2011）。这些技术可以单独使用，也可以通过使用多种算法进行集成技术，这可能会导致更好和更准确的检测结果。异常检测中一种流行的集成学习方法是RF算法。深度学习异常检测技术近年来崭露头角，在解决现实问题方面表现出明显更好的性能。这些包括各种类型的神经网络（NN）架构，如卷积神经网络（CNN）、长短期记忆网络（LSTM）等。近期文献中越来越受关注的其他深度学习架构包括自动编码器（AE）和生成对抗网络（GAN）（Fiore, De Santis, Perla, & Zanetti, 2019；Wang等，2020）。

检测保险欺诈的技术范围似乎比检测信用卡欺诈的技术范围更有限。近年来，许多研究努力似乎已经转向专注于后者。我们注意到这是一个近年来的趋势变化，因为Ngai等人的研究表明，金融欺诈检测技术的最突出研究领域是保险欺诈（Ngai等，2011）。与信用卡欺诈类似，早期和最流行的应用于检测保险欺诈的技术之一是朴素贝叶斯（NB）分类器、LR、DT、SVM等（Viaene等，2002）。近年来，深度学习模型如多层感知器（MLP）在这一任务中引起了越来越多的研究关注，研究工作甚至探讨了文本挖掘和自然语言处理（Wang & Xu, 2018）。

在本节中，我们根据学习方法对近年来应用于金融欺诈检测的文献进行分类和回顾。涵盖的四种方法是监督、无监督和半监督方法，以及简要介绍基于图的方法。

5.1. 监督方法

i. 支持向量机（SVM）

支持向量机（Support Vector Machines，SVMs）通过将输入空间映射到更高维的特征空间来寻找最优的分离超平面。它们可以在不引入任何额外计算复杂性的情况下实现这一点（Cortes & Vapnik, 1995）。SVMs的能力在处理许多

表5

基于SVM的欺诈检测的文献综述。

年份	参考文献	欺诈类型	方法	评论
2011	(Sahin & Duman, 2011)	信用卡	SVM	使用分层抽样的SVM过拟合数据，性能不及决策树。
2011	(Bhattacharyya et al., 2011)	信用卡	SVM	逻辑回归优于SVM。随着欺诈率降低，结果变得可比。
2011	(Lu & Ju, 2011)	信用卡	ICW-SVM	ICW-SVM优于SVM和决策树，并且在计算上更高效。
2013	(Hejazi & Singh, 2013)	信用卡	OCSVM	单类SVM在不平衡数据集中优于SVM。
2020	(Rtayli & Enneya, 2020)	信用卡	随机森林和SVM	RF-SVM集成的准确性与LOF-IF相当，但表现出最高的AUC。
2012	(Xiaodong, 2012)	汽车保险	DFSVM	DFSVM在F-分数、召回率和精确度方面优于普通SVM。
2015	(Ravi, 2015)	汽车保险	$k RNN -$ OCSVM $^{\text {a }}$	SVM模型的AUC和召回率显著增加，但精确度下降。
2016	(Sundarkumar, Siddeshwar, 2015)	汽车保险	OCSVM $^{\mathrm{a}}$	$k$ RNN被发现稍微限制了整体性能，因此被淘汰。

[^1] 通过欺诈检测系统而不是实际分类器进行增强。由于其提取相关重要特征的能力，使其在涉及高度不平衡数据集的检测任务中备受青睐。核函数是实现这一点的机制，这要归功于SVM具有核表示属性。SVM的另一个属性是边界优化，这是由于选择超平面的标准，通过最大化两类之间的间隔来最小化过拟合。

对于输入空间 $\mathrm{X}$ 和更高维空间 $\mathrm{H}$ ，核函数 $k$ 被定义为 $k\left(x_{1}, x_{2}\right)=\left\langle\left(\Phi\left(x_{1}\right), \Phi\left(x_{2}\right)\right\rangle\right.$ ，其中 $\Phi: \mathrm{X} \rightarrow \mathrm{H}$ 是将输入空间转换为更高维空间的映射。核函数的选择取决于应用和任务的性质，最常用的是多项式函数、径向基函数和线性函数。

Sahin和Duman（Sahin & Duman, 2011）应用SVM来检测欺诈性信用卡交易，并指出了实验中涉及的数据集的高度不平衡性质。为了克服这一问题，作者使用分层抽样来对数据集的合法案例进行欠采样，使其数量有意义（Sahin & Duman, 2011）。这包括数据预处理，首先确定在区分欺诈和合法交易方面最成功的特征。然后使用这些变量形成合法记录的分层样本，随后与欺诈记录组合。使用从一家国家银行获得的数据，作者将所提出的方法与各种类型的决策树（如C&RT、C5.0和CHAID）进行了比较（Sahin & Duman, 2011）。结果显示，决策树模型在测试集上的表现优于SVM模型，但与训练集准确性相比则相反（Sahin & Duman, 2011）。C5.0的训练集和测试集准确性分别为 $\%$ 和 $\%$ ，为最佳表现。尽管选择了不同的核函数，SVM模型的训练集和测试集准确性均为 $\%$ 和 $\%$ ，表现相同（Sahin & Duman, 2011）。这两组数据之间的性能差异导致文献中的结论认为SVM倾向于过拟合训练数据。然而，随着训练数据量的增加，这种过拟合行为变得不那么显著，性能变得可比（Sahin & Duman, 2011）。作者建议探索其他技术，如多层感知器（MLPs），并扩展性能指标以提供更详细的比较。

Bhattacharyya等人进行了类似的研究，实施SVM、逻辑回归和随机森林（RF）来检测欺诈性信用卡交易进行比较（Bhattacharyya et al., 2011）。RF是一种基于DT的监督集成方法，解决了DT中的不稳定性和可靠性问题，这些问题之前未被Sahin和Duman讨论过（Bhattacharyya et al., 2011; Sahin & Duman, 2011）。RF构建了与装袋结合的DT集成，并被认为是DT的首选集成方法（Bhattacharyya et al., 2011）。使用从一家国际信用卡公司获得的数据集，作者提取了定制属性，以解决信用卡数据的高维度和异质性问题。作者还建议对数据进行随机欠采样，特别是多数类，因为这通常优于其他抽样方法（Bhattacharyya et al., 2011; Van Hulse, Khoshgoftaar, & Napolitano, 2007）。数据集的异常标签总共为2,420个，分为1,237和1,183个交易的两个子集，使用第一个集合填充四个带有正常标签的训练集，第二个集合用于测试。四个训练集分别填充了不同数量的合法交易，以创建 $15, 10, 5$ 和2%的欺诈率进行交叉验证和比较。实验结果导致作者建议RF表现出整体更好的性能。然而，SVM在精确度和 $\mathrm{F}$ -分数方面优于逻辑回归，后者是精确度和召回率的调和平均值（Bhattacharyya et al., 2011）。SVM的准确度为 $\%$ ，略低于逻辑回归的 $\%$ 和RF的 $\%$ 。SVM的召回率为 $\%$ ，低于RF的 $\%$ 。

与先前的研究结果类似，随着数据集规模的增加和欺诈率的降低，SVM的性能变得可比（Bhattacharyya et al., 2011）。此外，所有三种技术在识别和正确分类正常交易方面的性能明显优于欺诈类别（Bhattacharyya et al., 2011）。从特异性值的范围可以看出，逻辑回归的最低特异性为 $\%$ ，SVM为 $\%$ ，RF为 $\%$ 。总体而言，RF在所有性能指标上表现优于其他技术，能够捕获更多的欺诈案例并减少假阳性。作者还指出RF的吸引力在于其计算效率和实施简单性，只有两个可调参数（Bhattacharyya et al., 2011）。

最后，文献总结指出，这些结果是在没有对SVM进行任何参数调整的情况下实现的，这可能会对其性能产生重大影响。因此，未来研究建议进一步研究参数调整，并研究不同类型欺诈行为之间的差异，例如盗窃和伪造卡之间的差异，以提取更全面的欺诈表示属性（Bhattacharyya et al., 2011）。

Lu和Ju还提出了一种不平衡类加权支持向量机（ICWSVM）用于信用卡欺诈检测，通过利用主成分分析（PCA）这种降维技术来解决大规模和维度问题（Lu & Ju, 2011）。这涉及提取捕获原始数据特征分布的主成分，保留信息的关键特征。所提出的方法使用高斯核函数来映射支持向量。ICW-SVM通过允许调整正常和欺诈类的权重来处理不平衡数据问题，根据需要改变超平面位置（Lu & Ju, 2011）。这消除了使用SMOTE、随机欠采样等抽样技术来平衡数据集的需要。
表6

从信用卡数据派生的属性结构（ $\mathrm{Lu} \& \mathrm{Ju}, 2011$ ）。

关键特征	内容
账户的负面信息 $\left(\mathrm{X}_{1}\right)$	违约频率，每个周期未偿信用余额
持卡情况 $\left(\mathrm{X}_{2}\right)$	透支频率，透支限额，最大逾期天数
交易频率 $\left(\mathrm{X}_{3}\right)$	消费日期，购物频率，商店代码，平均消费次数
交易次数比 $\left(\mathrm{X}_{4}\right)$	历史上每日交易次数/最大交易次数
基本客户信息 $\left(\mathrm{X}_{5}\right)$	年龄，教育程度，职业，收入，住房条件，行业前景

当进行主成分分析（PCA）时，支持向量机（SVM）在数据集规模扩大时具有更高的计算效率。与不使用PCA的相同方法相比，执行PCA的提出方法几乎快了四倍，只牺牲了 $1.4\%$ 的准确度，达到了 $90.9\%$ （Lu & Ju, 2011）。作者推断，由于其可扩展性，提出的模型在真实数据环境中将实现更好的性能。建议进一步研究如何有效选择正确的参数和核函数以增强所提出技术的性能。

尽管被认为是一种无监督异常检测技术，一类支持向量机（OCSVM）是由Schölkopf等人提出的一种基于核的SVM方法（Schölkopf, Williamson, Smola, ShaweTaylor, & Platt, 2000）。它们仅在数据的正常实例上进行训练，例如合法交易，以学习围绕这些点的边界。不在边界内的任何点都被分类为异常。在OCSVM中，通过核函数将输入数据映射到特征空间，以找到一个分隔超平面，但与常规SVM的主要区别在于，分隔超平面位于数据点和原点之间（Schölkopf等人，2000）。正如其名称所示，超平面被优化为将数据分为一个类（例如合法交易），使得未分组到该类的所有样本被视为异常类（例如欺诈交易）。基于（Schölkopf等人，2000）的二维空间中分隔超平面的图形表示示例如图2所示。这种OCSVM方法最为普遍，因为其实现和应用简单；然而，还存在其他方法（Hejazi & Singh, 2013）。Tax和Duin在（Tax & Duin, 2001）中描述了在异常和正常类之间使用超球面边界作为超平面的替代方法。

Hejazi和Singh提出了一种OCSVM方法，用于使用各种类型的核函数（如线性、多项式和径向基函数）对信用卡欺诈进行分类（Hejazi & Singh, 2013）。作者使用了来自加州大学欧文分校（UCI）存储库的德国信用卡数据集，该数据集共有1,000个样本和20个特征，其中300个样本属于异常类（University of California, 2000）。文献将平衡二元分类SVM与提出的OCSVM在不平衡数据集上进行了比较。OCSVM的参数是经验确定的，并在文献中概述，以观察这些参数对模型性能的影响。

在平衡数据集上训练的SVM模型中，随机抽样和扩展子抽样的测试准确率均为 $88.99\%$ ，而不平衡数据集的测试准确率为 $83.44\%$ 。然而，不平衡数据集的SVM具有最佳的测试集准确率为 $77\%$ ，而随机抽样的准确率为 $68\%$ ，排名第二。这导致结论认为，虽然在平衡数据上表现略有改善，但SVM往往会过拟合并泛化能力较差（Hejazi & Singh, 2013）。另一方面，与提出的OCSVM相比，结果显示，具有不平衡数据集的OCSVM明显优于具有平衡数据集的常规SVM，后者往往会过拟合训练数据（Sahin & Duman, 2011; Hejazi & Singh, 2013）。线性核函数的OCSVM具有最高的训练集准确率为 $90.16\%$ 和测试集准确率为 $91\%$ 。三次多项式核函数的准确率为 $90\%$ ，但测试集准确率最高为 $92\%$ 。径向基函数核在训练和测试集准确率方面表现相当，分别为 $89.66\%$ 和 $91\%$ 。总体而言，Hejazi和Singh提出的OCSVM模型表现出优越的性能，与先前发表的文献中的SVM方法相比，能够很好地泛化到未见数据，而不是过度拟合训练集（Hejazi & Singh, 2013）。OCSVM的计算效率也更受青睐，至少比SVM快两倍，并且无论使用何种核函数，平均执行时间都不到 $0.1\mathrm{~s}$ 。文献明确指出，参数调整和优化对OCSVM的性能至关重要，如果忽略这一点，可能会导致模型准确性严重下降（Hejazi & Singh, 2013）。

最近在2020年由Rtayli和Enneya发表的研究提出了一种基于RF作为特征选择算法的增强型信用卡欺诈检测方法，结合SVM来检测异常交易（Rtayli & Enneya, 2020）。RF算法从数据中选择相关特征，以提高后续SVM模型的整体性能，该模型负责将交易分类为合法或欺诈。通过利用重要性评分选择非冗余和稳健特征，可以减少数据的维度（Rtayli & Enneya, 2020）。使用准确率、召回率和曲线下面积（AUC）等指标，将此技术与其他方法（如DT，以及局部离群因子（LOF）和隔离森林（IF）等无监督技术）进行了比较，这些将在后续章节中进一步讨论。作者使用了从Kaggle（Machine Learning Group. (2017), 2017）获取的欧洲信用卡交易的公共数据集，共有284,807笔交易，其中492笔为欺诈交易。结果显示，提出的RF和SVM模型的准确率为 $95.18\%$ ，低于其他模型。此外，提出的模型在召回率方面远远优于其他模型，为 $87\%$ ，IF排名第二，为 $34\%$ 。提出模型的AUC为 $91\%$ ，也表现优于LOF的 $52\%$ ，IF的 $67\%$ 和DT的 $50\%$ 。总体而言，可以得出结论，基于RF特征选择的SVM具有良好的准确性，较少的误报警，并且在检测欺诈交易方面最为稳健（Rtayli & Enneya, 2020）。

对于欺诈汽车保险索赔的检测，Tao等人提出了一种双成员模糊支持向量机（DFSVM）（Tao, Zhixin, & Xiaodong, 2012）。在这种技术中，模型为每个样本分配两个成员值，表示属于每个类的概率。这导致模型利用了两倍数量的训练样本，有助于克服SVM的过拟合问题（Tao, Zhixin, & Xiaodong, 2012）。本文中选择的核函数是径向基函数（RBF）；然而，并未提供关于选择核函数的理由的讨论。提出的模型与常规SVM进行了比较，使用了北京的汽车保险案例数据。共使用了800个样本，一半为合法案例，另一半为欺诈案例。我们注意到，文献通过选择每种情况的样本数量，使数据集平衡，而不使用适当的抽样方法或技术，引入了偏见。数据集的分类特征被转换为数字编码，这对于这种类型的模型是必要的。通过使用网格参数搜索和交叉验证技术对模型的超参数进行调整。实验结果显示，提出的DFSVM在性能上优于先前的SVM方法，从F分数分别为 $91.02\%$ 和 $87.99\%$ 可以看出。DFSVM的召回率和精确率也是最高的，分别为 $91.31\%$ 和 $90.73\%$ 。作者最后通过重申引入模糊类成员资格对以前发表的文献中的技术进行改进来得出结论。
为了观察他们的新型混合欠采样方法的性能，作者在合并的训练集上训练并比较了几种分类器，如LR、MLP、DT和SVM。结果显示，所有分类器的整体性能均有所提高，其AUC分数较原始不平衡数据集上训练的相同模型有所提高（Sundarkumar & Ravi, 2015）。SVM分类器表现出最佳的整体性能，AUC为75.14%，比在原始数据集上训练的SVM提高了12%。DT的AUC为74.71%，在整体性能方面排名第二。SVM和DT的性能相当接近，召回率分别为91.89%和90.74%。这表明了所提出的模型能够有效地检测和准确分类欺诈案例。两种模型召回率的提高伴随着特异性的牺牲，DT的特异性从99.83%降至58.69%。SVM的特异性下降幅度较小，从63.2%降至58.39%。这表明，通过所提出的混合欠采样技术，增加检测欺诈案例的代价是相应增加误报率。

最后，作者进行了 $t$ -检验以确定SVM性能的统计显著性。文献发现，就SVM的召回率而言，所有模型在统计上都存在显著差异，除了DT。因此，作者建议DT最适合于所提出的新技术，因为它在计算速度上更快，更重要的是，它产生了“if-then”决策规则，有助于解释提取的知识（Sundarkumar & Ravi, 2015）。根据这项研究的发现，作者建议进一步努力确定 $k RNN$ 的存在是否对所提出的模型产生影响。如果没有，那么可以假设OCSVM本身可以对多数类进行欠采样，具有可比较的预测性能和显著提高的计算速度（Sundarkumar & Ravi, 2015）。

因此，Sundarkumar等人（Sundarkumar, Ravi, & Siddeshwar, 2015）探讨了仅使用OCSVM对多数类进行欠采样，以确定方法中 $k RNN$ 的存在是否对性能产生影响。在他们的工作中，作者使用了Sundarkumar和Ravi在（Sundarkumar & Ravi, 2015）中采用的相同数据集和方法。相反，选择OCSVM来处理大多数类中的异常检测和移除，并根据支持向量的属性进行欠采样（Sundarkumar & Ravi, 2015）。所提出的技术与先前工作的结果进行了比较。实验表明，所提出的方法在AUC和DT、SVM模型的召回率方面都略有改善。这些发现导致结论认为 $k RNN$ 对分类性能没有显著影响（Sundarkumar, Ravi, & Siddeshwar, 2015）。然而，该论文并未调查或确定这些发现带来的时间和经济节约，这可能是未来研究的一个方向。

ii. 神经网络（NN）

神经网络是一种计算算法，模拟人脑的工作原理，使用称为神经元的元素（Ngai等，2011）。每个神经元都有与其连接相关联的权重和偏置，网络结构通常包括放置在三个主要层内的任意数量的神经元：输入、隐藏或输出层。这些网络通常是密集连接的，这意味着输入神经元与隐藏层中的每个神经元相连，然后这些神经元也与输出层中的每个神经元相连。

在本节中，我们主要关注前馈神经网络，也称为多层感知器网络（MLP），这是最简单的神经网络类型。这些网络将输入沿着从输入层到输出层的方向向前传播（Michelucci，2018）。图3显示了一个密集连接的NN的图形示例。网络的每个神经元将其输入视为前一层神经元的输出。除了输入层外，每个神经元的输出在成为下一层的输入之前必须经过激活函数。激活函数的选择取决于应用，但最常用的是Sigmoid函数或修正线性单元。属于监督学习的神经网络必须使用学习算法从数据集中学习。其中最常用的算法之一称为误差反向传播，涉及根据训练数据计算误差。然后，这个误差向后传播通过网络，使用梯度下降相应地校正神经元的权重和偏置（Maes & Tuyls，2002）。实施MLP用于欺诈检测的论文综述摘要见表7。

1993年，Maes等人描述了用于信用卡欺诈检测的MLP的首次实现（Maes & Tuyls，2002）。作者在带标签的交易数据集上使用标准反向传播训练了一个标准NN。在进行的两个实验中，第一个实验涉及研究数据集预处理的效果。经过相关性分析，发现十个特征提供了最显著的结果，这意味着删除一个特征（Maes & Tuyls，2002）。这导致了MLP的最佳结果，其中对于70%的真正阳性，只有15%的假阳性。第二个实验突出了参数调整的重要性，这影响了学习过程。作者指出，通过在特定间隔降低学习率，可以提高速度和效率（Maes & Tuyls，2002）。结果显示，MLP产生了良好的结果；然而，在性能方面，它被贝叶斯网络超越。此外，在所需的训练时间方面，MLP比贝叶斯网络要快得多。文献中对未来的建议包括修剪算法，以消除在训练过程中实际未使用的神经元和连接，以及在权重优化的反向传播的错误函数中使用变体，如径向基网络（Maes & Tuyls，2002）。
各种研究论文已经发表，提出了标准神经网络的各种变体，这些变体在先前的文献中已经被使用。在信用卡欺诈的情况下，Patidar 和 Sharma 提出并讨论了使用遗传算法（GA）来决定 $\mathrm{NN}$ 的拓扑结构，即神经元应该如何相互连接，最常见的方式是全连接和三层结构（Patidar & Sharma, 2011）。这是为了解决神经网络的一个问题，即缺乏关于设置网络中那些对学习和性能起关键作用的参数的明确指导（Patidar & Sharma, 2011）。尽管提出的研究看起来很有前景，但作者并没有通过实验分析其可行性。

Khan 等人提出使用模拟退火（SA），这是一种基于热力学热处理过程的概率技术，作为神经网络的训练算法（Khan, Akhtar, & Qureshi, 2014）。作者证明了这种技术可以解决标准反向传播在局部最小值处停滞的问题，并且在计算上比其他元启发式算法如 GA 更经济（Khan, Akhtar, & Qureshi, 2014）。作者使用了来自 UCI 数据库的数据集，设计了一个包含 20 个输入神经元的 MLP，每个神经元代表数据集的一个特征，并且有两个输出代表二元分类器，在隐藏层中有任意的 50 个神经元（University of California, 2000）。该模型在原始数据集的 $\%$ 上训练完成需要两天时间，导致 $\%$ 的训练误差。实验表明，该模型具有良好的检测准确率，识别出 $\%$ 的欺诈案例和 $\%$ 的合法案例。这表明在检测更多欺诈案例和假阳性率之间存在权衡（Khan, Akhtar, & Qureshi, 2014）。一个未解决的问题是模型完成训练所花费的大量时间，这表明它可能比作者预期的更昂贵。

鲸鱼优化算法（WOA）是由 Wang 等人于 2018 年最近提出的，作为一个用于 MLP 的学习算法，旨在解决收敛到局部最小值缓慢和反向传播技术稳定性低的问题（Wang, Wang, Ye, Yan, Cai, & Pan, 2018）。WOA 是 Mirjalili 和 Lewis 在 2016 年提出的一种新颖的元启发式算法，作者在他们的文献中展示了 WOA 相对于最先进的元启发式算法非常有竞争力（Mirjalili & Lewis, 2016）。作者使用了欧洲数据集，其中包含 284,807 笔交易，其中有 492 笔是欺诈交易。PCA 被用来找到数据的低维表示，通过 8 个主成分保护客户隐私。实验结果表明，使用 WOA 来更新 MLP 的权重导致出色的性能，模型实现了 $\%$ 的 F 分数，准确检测了 $\%$ 的欺诈交易和 $\%$ 的正常交易（Wang 等人，2018）。与使用其他元启发式算法如 GA 训练的模型相比，WOA 在各个指标上表现更好。作者还指出，所提出的技术展示了出色的泛化能力。

在他们的研究中，Viaene等人进行了一项基准基准研究，通过实证评估了DT、SVM和提出的BNN模型在检测欺诈性汽车保险索赔方面的表现（Viaene等人，2002年；Viaene等人，2005年）。使用了一个数据集，其中包含了1992年在马萨诸塞州提出的1,399项索赔。数据中的信息由马萨诸塞州汽车保险公司收集，跟踪了25个二进制特征以及12个连续的分类特征，这些特征被认为与欺诈调查员和理赔员相关。文献显示，BNN在AUC分数方面一直优于其他模型（Viaene等人，2005年）。提出的BNN的AUC达到了 $\%$ ，而DT和SVM分别仅为 $\%$ 和 $\%$ 。然而，就准确性而言，SVM表现最佳，达到了 $\%$ 。然而，提出的BNN和DT的准确率仍然达到了 $\%$ ，与SVM相比差异微乎其微。一个重要的注意是，作者没有提及或讨论数据中欺诈案例的分布以及其是否具有平衡性质。

Xu等人提出了一个MLP集成，使用基于粗糙集理论的降维技术对原始数据进行预处理（Xu, Wang, Zhang, & Yang, 2011年）。粗糙集方法已经证明能够显著降低模式的维度，被证明适用于神经网络的前端，这个主题已经被Thangavel和Pethalakshmi广泛审查（Thangavel & Pethalakshmi，2009年）。在他们的研究中，Xu等人（Xu, Wang, Zhang, & Yang, 2011年）使用粗糙集减少技术生成了训练数据的多个减少子集。文献中使用的数据集与Sundarkumar和Ravi在（Sundarkumar & Ravi，2015年）提出的研究中使用的数据集相同，该数据集包含了来自一家保险公司的15,420份汽车索赔样本。作者通过采用随机子空间方法，也称为特征或属性装袋，进一步扩展了他们的方法，随机选择一个生成的减少子集来训练每个MLP分类器的集成。然后使用投票或加权投票策略对每个MLP的预测进行聚合，然后将模型的最终输出与测试集进行比较。

对几种不同的MLP进行了实验，并与验证了提出方法的性能，首先是使用动量梯度下降和自适应学习率进行训练的MLP（Xu, Wang, Zhang, & Yang，2011年）。另外使用了一步割线反向传播和弹性反向传播这两种类型的MLP。对所有模型的准确性和ROC曲线进行了比较，作为研究方法中概述的两个分类器的集成。如预期的那样，所有三个模型的准确性都有所提高。单个分类器实现的最高准确性是一步割线MLP的 $\%$ ，其次是梯度下降MLP的 $\%$ 和弹性反向传播MLP的 $\%$ （Xu, Wang, Zhang, & Yang，2011年）。集成配置中记录的最高准确性为 $\%$ ，由梯度下降与动量和一步割线MLP共同实现。作者没有评估每个模型的AUC，而是简单地提供了每个模型的ROC曲线的视觉比较，无论是单个还是集成配置。研究论文中没有讨论为每种提出的技术提供的ROC。然而，我们注意到通过视觉检查，一步割线MLP的ROC更接近图表的左上角。这表明一步割线MLP具有更高的召回值，意味着更有效地检测欺诈索赔，减少了虚警。作者提出的未来研究工作包括探索其他类型的集成分类模型，其他类型的欺诈，以及将提出的系统应用于在线欺诈检测（Xu, Wang, Zhang, & Yang，2011年）。

Wang和Xu的研究利用深度学习和文本挖掘提出了一种新颖的技术，用于检测汽车保险欺诈（Wang & Xu，2018年）。先前关于保险欺诈检测的大多数研究都是检查数值或分类因素，例如索赔提交时间或被保险车辆的品牌、型号或颜色。然而，保险索赔中的文本信息很少被研究或分析以检测欺诈。因此，作者提出使用基于潜在狄利克雷分配（LDA）的文本分析来提取索赔人提供的索赔描述中的隐藏文本特征（Wang & Xu，2018年）。随后，MLP在带有提取特征的标记数据上进行训练，以学习检测欺诈性索赔。在自然语言处理中，LDA是由Blei等人提出的一种生成概率模型，它使用贝叶斯模型来提取和建模文本中的主题作为概率分布（Blei, $\mathrm{Ng}$ , & Jordan，2003年）。每个主题被认为是彼此独立的，也可以被视为文档中许多单词的概率分布（Wang & Xu，2018年）。文献中引入了一个困惑度术语，以帮助确定适当的主题数量。该术语衡量了概率分布的预测能力，更适当的概率分布具有相对较低的困惑度值（Wang & Xu，2018年）。

作者使用了一家汽车保险公司的真实数据集，包含了37,082个标记样本。数据集中有415个欺诈性索赔，占数据集的 $\%$ ，突显了数据集的不平衡性质。因此，建议对多数进行过采样，使用SMOTE方法，使每个合法和欺诈类别的数据集增加到1,660个样本。每个样本描述了10个特征，其中一个是文本属性，将使用LDA处理该属性，提取关键隐藏主题，并将其作为分类特征添加到数据集中。为了防止过拟合，进行了10折交叉验证训练，使用了10个不同主题组数量的LDA。模型的最低困惑度是由具有五个主题的模型实现的，每个主题代表了索赔中专家审计员描述的某些词语-每个主题中最重要的单词在表8中列出。

在第一个主题中，这些词语描述了事故的责任、车辆驾驶员和第三方的责任。第二个主题描述了个人如何处理事故，因为有些人可能会向警察报告事故，而其他人可能会接受私人方提供的赔偿（Wang & Xu，2018年）。主题3描述了事故现场的情况，以及是否有目击者或警察介入。根据人类专家个人经验的描述或账户，驾驶行为主要分布在从主题4中得出的关键词中。关于事故导致的任何损害或人身伤害的信息包含在主题5中。作者希望在这些附加特征上训练的MLP能够提取领域专家的经验。

MLP架构包括七个隐藏层，这是根据经验确定的，因为观察到在七个隐藏层之后，计算量增加而性能没有改善（Wang & Xu，2018年）。通过手动调整，选择了每个层中节点的数量为8、8、10、7、8、6和4。神经元中使用ReLU激活函数以避免梯度消失问题，并且为每个神经元采用了0.2的丢失概率，以帮助遏制过拟合。此外，MLP使用自适应学习率，从0.5开始，并随着时代的增加而减少。提出的模型与RF和SVM进行了比较，并发现其召回率为 $\%$ ，比RF高出 $\%$ ，比SVM高出 $\%$ 。这被认为是由于深度学习模型能够捕获和理解LDA提取的抽象经验（Wang & Xu，2018年）。具有LDA提取特征的MLP模型的准确性和精确度分别为 $\%$ 和 $\%$ ，是三种模型中最高的，至少高出 $\%$ 。提出模型明显的整体优越性进一步得到支持，其F分数为 $\%$ ，而RF为 $\%$ ，SVM为 $\%$ 。

作者还在其研究中进行了比较分析，将三种模型分别与不使用基于LDA的文本挖掘和特征提取方法的模型进行了比较。对于没有LDA的MLP，确定了最佳结构，其中包括每个层中6、7、9、4、5、4和4个神经元的七个隐藏层，使用了与先前实验类似的ReLU激活函数。结果显示，没有LDA的MLP整体性能下降，F分数降低了 $\%$ ，降至 $\%$ 。在召回率方面，性能下降也很显著，为 $\%$ ，比使用LDA的提出模型降低了 $\%$ 。总的来说，具有LDA的MLP模型被证明是最佳的欺诈性索赔检测器。作者指出，从人类专家提取的文本描述的分析可能不可避免地涉及主观想法或特征。因此，文献建议探索消除这些特征的方法。

表8

LDA提取的五个主题的关键词（Wang & Xu，2018年）。

主题	关键词
1	现场、驾驶员、第三方、责任
2	报告、处理、赔偿
3	警察、权利、碰撞
5	前置、背面、玻璃、无伤害、受损

观察隐性偏见的效果并使模型更好地泛化（Wang & Xu, 2018）。

iii. 卷积神经网络（CNN）

CNN 是另一种深度学习架构，最早在上世纪 90 年代引入，其特点是具有许多层，分为输入、池化、全连接和输出层（LeCun & Bengio, 1998）。它们的命名来源于卷积层对输入执行的一种数学运算，即卷积。图 4 显示了 CNN 层结构的表示。由于输入通常以矩阵形式呈现，CNN 主要用于基于图像的模式识别任务（O’Shea & Nash, 2015）。然而，通过操纵输入数据的结构，它们已被证明适用于其他领域和领域。

正如图 4 所示，CNN 架构的各个层负责执行不同的操作。如前所述，卷积操作在卷积层中执行，保留输入的空间关系以提取派生特征。使用不同的滤波器进行卷积操作，充当特征检测器。池化层使用子采样技术减少从卷积层产生的特征图的维度，保留最关键的信息。池化使输入更易处理，减少网络中的计算量和参数数量，有助于控制过拟合（Krizhevsky, Sutskever, & Hinton, 2012）。全连接和输出层是传统的密集连接前馈 NN 或 MLP，其输入是来自卷积和池化层的输出，并用于对数据进行分类。涉及基于 CNN 方法的相关作品可见于表 9。

Fu 等人于 2016 年首次提出了将 CNN 用于信用卡欺诈检测任务，以从标记数据中捕获欺诈行为的内在模式（Fu, Cheng, Tu, & Zhang, 2016）。作者提出这种方法是为了应对 MLP 的过拟合行为。他们使用了一家商业银行的标记信用卡数据集，并对其进行了调整，提出了一种捕获数据中时间表示的特征转换方法。这涉及将数据的特征分成几组，这些组在不同的时间窗口内具有不同的特征，通过这种方式，同一类型的两个不同时间窗口的特征之间存在强关联，因此它们在特征矩阵中的位置会靠近（Fu, Cheng, Tu, & Zhang, 2016）。从原始数据中导出了新特征，例如平均交易金额、当前金额与平均金额之间的差异，以及为固定时间窗口生成的其他特征。作者提出了一种新颖的特征来描述用户交易金额与一段时间内的总交易金额之间的关系，称为交易熵，这一特征被实现到模型中（Fu, Cheng, Tu, & Zhang, 2016）。

原始的一维特征向量被重塑为一个特征矩阵，其中行代表不同的特征，而

图 4. CNN 层的结构示意图及相关功能。

表 9

关于基于 CNN 和 LSTM 的欺诈检测的已发表文献摘要。

年份	参考文献	欺诈类型	方法	评论
2016	Fu 等人（Fu, Zhang, 2016）	信用卡	CNN	CNN 实现了 0.33 的 F 分数，胜过 MLP。
2017	Heryadi 和 Warnars（Heryadi & Warnars, 2017）	信用卡	CNN-LSTM	CNN 的短期和 LSTM 的长期能力结合捕获时间关系。最佳 AUC 达到 $\%$ 。
2018	Zhang 等人（ Zhang et al., 2018）	信用卡	CNN	CNN 实现了 94% 的召回率和 91% 的精度，胜过 MLP，但在训练中速度较慢。
2009	Wiese 和 Omlin（ Wiese & Omlin, 2009）	信用卡	LSTM	LSTM 胜过 SVM，以及 Maes 等人在 (Maes & Tuyls, 2002) 中提出的 MLP。
2018	Jurgovsky 等人（ Jurgovsky et al., $2018)$	信用卡	LSTM	具有特征聚合策略的 LSTM 表现与 RF 类似，但检测到不同的欺诈行为。建议模型组合。

列代表不同的时间窗口。通过生成热图来说明欺诈和合法交易之间的相关性。实验结果讨论有限，但显示具有交易熵的 CNN 模型实现了 0.33 的 F 分数，相较于其他技术如 MLP、SVM 和 RF，被认为更优秀（Fu, Cheng, Tu, & Zhang, 2016）。

Heryadi 和 Warnars 发表的进一步研究评估了 CNN 在预测欺诈交易方面的性能，将其与 LSTM 和混合 CNN-LSTM 模型的性能进行了比较（Heryadi & Warnars, 2017）。混合模型试图结合 CNN 和 LSTM 模型分别捕获短期和长期关系的能力。银行的卡交易数据经过欠采样处理，以捕获支出模式的短期和长期关系构建了自定义特征。

构建的特征包括 50 个元素的向量，每个向量代表持卡人一个月内的历史交易，如每日交易金额、连续两天的平均交易金额以及整个月份的最小和最大金额（Heryadi & Warnars, 2017）。使用 PCA 确定特征集的主成分以减少维度，实验试验比较了使用 20、30 和 40 个主成分时的性能。作者指出，AUC 是识别最佳执行模型的最合适指标，在所有试验中，使用不同数量的主成分时，CNN 模型被实验确定为表现最佳的模型（Heryadi & Warnars, 2017）。在 CNN 模型中，使用 30 个主成分实现了最高的 77% 的 AUC，作者指出 CNN 在所有模型中具有最小的准确度得分。可以推断出，CNN 模型在最小化假阳性数量以捕获更多欺诈案例方面做出了妥协。作者解释 CNN 优越性的结果是由于其在捕获短期趋势方面的优势，与欺诈者通过信用卡进行欺诈交易的短期性质相对应（Heryadi & Warnars, 2017）。

张等人进行的研究旨在利用 CNN 检测欺诈交易的结果支持了此技术在该应用领域的有效性的先前发现（Zhang, Zhou, Zhang, Wang, & Wang, 2018）。然而，作者指出，他们提出的模型可以仅使用交易数据的原始特征进行训练而实现比现有 CNN 模型更好的性能。商业银行提供的交易数据包括 6 个月内的 500 万笔交易，具有 62 个维度，正样本约为欺诈样本的 33 倍。通过使用一个月的数据批次来确保数据的连续性。通过特征工程方法和对原始数据的统计分析，确定了用于欺诈检测模型的数据集中的显著特征，从而将输入减少为 8 维，直接输入到模型中。作者在输入层之前实现了一个特征序列化层，将特征排列成一维向量特征，通过卷积层中的一维卷积核特征向量进行处理。根据（Zhang et al., 2018），图 5 描绘了一个 $\times 2$ 的卷积核，显示了转换过程，从两个相邻特征生成派生特征。

iv. 长短期记忆网络

图5. 一个 $\times 2$ 卷积核在两个特征之间的卷积过程。

长短期记忆网络（Long Short-Term Memory networks，LSTM）是循环神经网络（Recurrent Neural Networks，RNN）的一种扩展，是一种深度神经网络，主要用于时间序列数据，由Hochreiter和Schmidhuber于1997年提出（Hochreiter & Schmidhuber, 1997）。LSTM中的每个神经元都是一个带有“记忆”的单元，可以存储信息，保持自己的状态，与RNN不同，RNN仅仅是从其先前的隐藏状态获取当前输入，以输出新的隐藏状态。LSTM的改进记忆能力归功于在单元中引入了输入和输出“门”，随后不久引入了遗忘门，由Gers等人提出（Gers, Schmidhuber, & Cummins, 2000）。关于LSTM和不同变体的详尽评论，我们建议读者参阅 $\mathrm{Yu}$ 等人最近的一篇调查论文（Yu, Si, Hu, & Zhang, 2019）。

LSTM目前在许多实际应用中处于领先地位，如文本、书写和语音识别，以及自然语言处理。它们也以解决通常与RNN相关的梯度消失问题而闻名（Hochreiter & Schmidhuber, 1997）。最近才将LSTM应用于欺诈检测，早期研究中已经讨论的是由Heryadi和Warnars进行的（Heryadi & Warnars, 2017）。其他作者也认可了这一点，如Gómez等人（Gómez et al., 2018），甚至有人建议LSTM在检测欺诈性信用卡交易或保险索赔方面表现出潜力。尽管有所承诺，但它们在研究中的应用很少，缺乏研究其在检测金融欺诈方面的性能的可用文献。有关基于LSTM方法的相关文献总结，请参见表9。

Wiese和Omlin（Wiese & Omlin, 2009）是最早探索使用LSTM开发信用卡欺诈检测模型的人之一。作者指出，目前的欺诈检测措施存在误分类问题，其实用性受到高误报率的影响（Wiese & Omlin, 2009）。文献提出，通过使用LSTM分析整个交易序列而不是单个交易，系统将能够捕获更多的时间关系和行为，最终对合法消费行为的轻微波动或转变更具鲁棒性（Wiese & Omlin, 2009）。在研究中，LSTM的架构中使用了标准门，如输入、输出和遗忘门。对数据进行了标准预处理，包括将符号特征（如交易数据）编码为数值，并进行标准手动特征选择。此外，还计算并使用了一种名为交易速度的统计值作为额外的输入特征。在欺诈情况下，交易速度是通过在预定时间范围内发生在账户中的交易数量来计算的（Wiese & Omlin, 2009）。可以通过将某些商家分组到一个速度计算中来计算不同的速度。

在他们的研究中，Wiese和Omlin比较了所提出的LSTM信用卡欺诈检测模型与另一个采用支持向量机（Support Vector Machines，SVM）的模型的性能（Wiese & Omlin, 2009）。使用了包含30,876笔交易的信用卡交易数据集，其中欺诈类占总案例的不到 $\%$ 。数据集根据交易日期和时间重新排序。将数据集的一半用于训练，另一半用于测试。确定用于LSTM的架构是通过经验分析确定的，包括两个具有两个记忆单元的记忆块，与输入和输出神经元密切连接（Wiese & Omlin, 2009）。共进行了30次试验，每次进行100个训练周期，这也是经验选择的，因为它导致了最佳的泛化性能。在模型训练过程中，如果发生误分类错误，则会重新开始当前交易序列的训练，并重复此过程，直到所有交易序列都被正确分类（Wiese & Omlin, 2009）。然后，从训练集中随机选择一个新序列进行下一次迭代，训练周期结束时，记录模型对训练集和测试集的预测，以绘制AUC曲线进行比较。

在进行的30次试验中，所提出模型在训练集和测试集上的平均AUC分别为 $\%$ 和 $\%$ ，展示了类别之间的显着分离（Wiese & Omlin, 2009）。正如作者所预期的那样，所提出的模型胜过了SVM，这被认为是一项显著的成就，因为SVM的表现也非常出色。SVM在测试集上实现了 $\%$ 的AUC。然而，文献表明，可能确定的核函数和超参数并非最优，需要更彻底的调整（Wiese & Omlin, 2009）。此外，LSTM的训练速度比SVM慢，但一旦训练完成，其分类速率要高得多，为每秒2,690笔交易，而SVM为每秒213笔交易。Wiese和Omlin（Wiese & Omlin, 2009）将LSTM欺诈检测模型与Maes等人提出的MLP技术进行了比较，并发现他们的模型在性能上更优秀。Maes等人提出的MLP在 $\%$ 误报率下的召回率为 $\%$ ，在 $\%$ 误报率下的召回率为 $\%$ ，而Wiese和Omlin的LSTM在 $\%$ 和 $\%$ 误报率下的平均召回率分别为 $\%$ 和 $\%$ （Maes & Tuyls, 2002; Wiese & Omlin, 2009）。

对模型的局限性进行了详细讨论，并提出了未来的研究建议以探索改进欺诈检测性能的途径。首先，指出将LSTM应用于一组不同长度的时间序列是一种过度复杂化，因此未来的努力可以用于使用LSTM来建模单一时间序列（Wiese & Omlin, 2009）。此外，研究中使用的网络拓扑结构相当简单，仅包括两个具有两个记忆单元的记忆块，这被归因于奥卡姆剃刀原则，简单地说是“最简单的解释通常是正确的”。然而，作者提到，这导致了更少的权重，为将这些权重存储在下一代支付卡芯片上打开了可能性（Wiese & Omlin, 2009）。这种实施的可能好处是，销售点终端将能够使用存储在芯片上的权重进行初始欺诈检测，仅将具有高度欺诈的交易转发到主机系统，减轻了一些负担（Wiese & Omlin, 2009）。本质上，这使得真正的在线欺诈检测系统成为可能，其中欺诈的检测甚至可能等同于其预防。最后，Wiese和Omlin还建议研究无监督方法，指出在许多情况下，实施在银行或相对新于这些技术的国家中的欺诈检测系统时，通常缺乏识别欺诈案例的记录或数据（Wiese & Omlin, 2009）。这消除了使用监督学习的可能性，而不借助人工专家进行手动标记，这既非常昂贵又效率低下。

Jurgovsky等人（Jurgovsky et al., 2018）提出了一种用于检测信用卡欺诈的LSTM模型，但与先前研究中模拟交易序列不同，作者们利用了Bahnsen等人在信用卡检测模型中明确提出的一种新颖的特征聚合方法（Bahnsen, Aouada, Stojanovic, & Ottersten, 2016）。特征聚合策略涉及将在最后指定的时间段内进行的交易分组，最初按照卡号或账号，然后按照交易类型、商家组、国家或其他方式进行分组，然后计算所有这些交易中的交易次数或总金额（Bahnsen等人，2016）。

Bahnsen等人指出，聚合特征仍然存在未捕获的信息，他们进一步通过推导时间特征将方法提升一步（Bahnsen等人，2016）。这涉及分析交易时间，其理由是预期客户会在相似的时间进行交易。在分析时间特征时会出现问题，特别是在查看某些交易时间的平均值时，这是因为很容易犯使用算术平均值的错误。算术平均值不考虑时间特征的周期性行为。例如，四笔交易时间分别为2:00、3:00、22:00和23:00的算术平均值为 $12 : 30$ ，这是不合理的，因为在该时间附近或在该时间没有进行交易（Bahnsen等人，2016）。为了克服这一限制，作者们提出使用von Mises分布将交易时间建模为周期变量，这是一种用于圆形数据的统计分析方法（Fisher, 1993）。这允许确定周期均值，这比算术平均值更真实地表示交易时间。
文献中采用了几种指标来比较两种分类器的性能，以及观察每次实验中检测到的欺诈类型的差异。选择这些指标是基于两个标准：对抗不平衡类别的鲁棒性，以及关注业务特定的细节和利益 (Jurgovsky 等人，2018)。首先是AUPRC，因其在欺诈检测中的不平衡设置中的益处和鲁棒性而备受关注。具体来说，AUPRC对假阳性的数量敏感，并捕捉了大量真实样本对分类器性能的影响 (Jurgovsky 等人，2018)。此外，Jaccard指数用于研究两种方法的定性差异，突出了基于所检测到的欺诈类型的分类器之间的相似性，以混淆矩阵的形式呈现。

根据实验结果，RF和提出的LSTM模型之间的性能没有明显区别，两者的表现相当。然而，在使用研究中提出的聚合特征时，两种分类器的性能均有明显改善。在面对面交易数据集中，使用短序列的情况下，LSTM的性能从 $\%$ 提高到 $\%$ ，RF从 $\%$ 提高到 $\%$ (Jurgovsky 等人，2018)。在训练中使用较长序列导致LSTM模型的性能稍微较弱，使用聚合特征时AUPRC为 $\%$ ，被RF的 $\%$ 超越。电子商务数据集显示了类似的趋势，但整体性能优于面对面数据集，其中长序列的LSTM和RF的AUPRC分别为 $\%$ 和 $\%$ (Jurgovsky 等人，2018)。这些AUPRC明显高于没有聚合特征的情况，进一步证明了该方法的可行性。最有趣的结果是使用Jaccard指数观察到的，该指数呈现了一个热图，比较了每种模型检测到的欺诈类型的相似程度。就每种模型检测到的欺诈类型与自身相比而言，两种模型在检测到的欺诈类型的相似性上保持一致。然而，这种特性在RF模型中略微更为显著，因为LSTM显示出稍微更多的变化。当然，当LSTM和RF模型相互比较时，显然LSTM捕获了更全面的不同类型的欺诈行为。此外，研究表明，这两种模型检测到的欺诈卡行为类型非常不同 (Bahnsen 等人，2016)。

Jurgovsky 等人推测，两种模型共同在欺诈检测系统中工作可能会带来更好的结果，因为两种模型检测到的欺诈类型不同，以及能够检测到更全面的欺诈交易类型 (Jurgovsky 等人，2018)。研究中还详细描述了关于LSTM架构的几点观察，尽管研究中没有提供具体细节，但作者提到当节点数量较少时，该模型容易过拟合 (Jurgovsky 等人，2018)。通过逐步增加节点数量来解决这个问题，结合ADAM优化器而非SGD可以产生最佳结果。

v. 朴素贝叶斯

朴素贝叶斯（NB）分类器是一种流行的监督模型，通常被认为是贝叶斯网络分类器的最简单形式（Friedman, Geiger, & Goldzsmidt, 1997）。该模型学习训练集中每个属性在给定类别标签的条件概率。然后，通过应用贝叶斯定理来计算给定特定实例的特征或属性的标签的概率进行分类（Friedman 等人，1997）。这种计算的可行性需要一个假设：数据集中的所有特征都独立于类标签的值。考虑输入数据 $x=\left(x_{1}, \cdots, x_{n}\right) \in \mathbb{R}^{n}$ 和目标标签 $y$ ，结构假设简化了模型：

$\mid y)=\prod_{m=1}^{n} p\left(x_{m} \mid y\right)$

对于许多领域来说，假设给定类别的预测变量是独立的可能有些过于严格。尽管如此，基于广泛的经验研究历史，NB分类器通常被报道表现出令人惊讶的良好性能（Viaene 等人，2002；Viaene, Derrig, & Dedene, 2004）。即使在基础独立性假设被认为不切实际的情况下，这也是真实的（Friedman 等人，1997）。

Viaene 等人的研究提出了使用NB分类器预测欺诈汽车保险索赔，类似于他们在之前研究中的工作（Viaene 等人，2002）。作者提出使用由Freund和Schapire提出的AdaBoost算法来增强模型（Freund & Schapire，1996）。Boosting的基本思想是按顺序构建分类器，这些分类器在原始训练集的各个版本上进行训练。各种训练集是通过重新采样或重新加权形成的，序列中一个分类器错误分类的任何数据实例在下一个模型中具有更重要的权重。在固定迭代次数后训练终止后，分类器使用多数投票方案组合。在AdaBoost中，根据其分类质量自适应加权每个分类器的投票（Ridgeway, Madigan, & Richardson, 1998）。逐步扰动数据的概念允许NB模型逐渐集中于更难学习的数据区域（Viaene 等人，2004）。所提出的模型进一步扩展为使用权重证据投票公式来处理NB与AdaBoost的情况，如Ridgeway等人所提出（Ridgeway, Madigan, & Richardson, 1998）。权重证据投票促进了更可解释的结果和解释，这些结果在AdaBoost中被消除，同时保留了NB分类器的预测性能（Ridgeway, Madigan, & Richardson, 1998）。

文献中使用了马萨诸塞州汽车索赔数据集，该数据集包含1,399个数据样本。数据集的三分之二用于训练提出的朴素贝叶斯AdaBoosted错误权重（ABWOE）分类器，该分类器由25个基本分类器的序列组成。该模型与简单的NB分类器、AdaBoost分类器（AB）以及使用多数投票而非提出的方法的模型进行了比较。对模型的评估基于准确性、AUC和对数分数 $(\bar{L})$ 的标准，使得 $\{\bar{L} \in[0, \infty)\}$ ，0为最佳（Viaene 等人，2004）。提出的ABWOE分类器在所有性能指标上表现优于其他模型，准确率为 $\%$ ，AUC为 $\%$ ， $\bar{L}$ 最低为0.3697。提出的投票框架被证实为优越，因为多数投票模型的AUC为 $\%$ ，表示没有区分能力，输出预测是随机猜测。普通NB的准确率为 $\%$ ，AUC为 $\%$ ，略低于ABWOE的性能。AB模型的准确率和AUC分别为 $\%$ 和 $\%$ 。这些结果与ABWOE相当，但提出的模型最终被认为优于 $A B$ ，因为 $\bar{L}$ 小于 $A B$ 的0.8789的一半。总之，作者认为ABWOE评分框架的易用性、可解释性和普适性是该模型的主要优势，允许灵活的人类专家交互和调整（Viaene 等人，2004）。

Phua 等人进行的类似研究研究了使用混合堆叠-装袋训练方法使用NB、C4.5 DT和MLP的影响（Phua 等人，2004）。研究的目的是解决与分类器性能不佳相关的倾斜或不平衡问题。装袋利用诸如NB之类的基本分类器，用随机抽样的训练数据子集进行拟合。然后，每个基本分类器对样本的类别进行投票，选择多数投票作为最终分类。装袋和提升的区别在于，在装袋中，模型独立地并行学习，而在提升中，模型按顺序相互学习。堆叠进一步利用装袋中基本模型的输出来训练元模型，以选择最佳基本分类器，然后将这些预测与装袋结合（Phua 等人，2004）。

表格10

保险欺诈检测成本模型的组成部分（Phua等人，2004年）。

索赔类型	成本
检测到的欺诈（DF）误报警（FAL）	检测到的案例数量 * 每次调查的平均成本误报警数量 *（每次调查的平均成本 + 每次索赔的平均成本）。
未检测到的欺诈（UDF）	未检测到的案例数量 * 每次索赔的平均成本
真实索赔（G）	真实索赔数量 * 每次索赔的平均成本

根据作者的说法，该模型的性能有两个极端。在一个极端，没有进行任何欺诈检测，所有索赔都被视为真实（无操作）。在另一个极端，模型实现了完美的性能，并且在没有误报警的情况下检测到所有欺诈索赔（最佳情况）。根据这些极端情况，Phua等人描述了成本模型如下（Phua, Alahakoon, & Lee, 2004年《欺诈检测中的少数派报告：偏斜数据的分类》）：

节省金额 $=$ 无操作 $- [U D F + F A L + G + D F]$

节省百分比 $=\frac{\text { 节省金额 }}{\text { 最佳情况 }} * 100 \%$

通过提出的模型进行的实验结果是使用开发的成本模型和整体准确性进行衡量的。与仅使用单个分类器、一组分类器或仅使用装袋技术的其他分类模型相比，提出的方法被认为更优越，因为它实现了最显著的成本节约，达到了 $$ 167,000$ 的节省，并且准确率仅为 $\%$ （Phua等人，2004年）。这些财务节约相比完美分类器减少了 $\%$ 的成本。其他模型，例如仅使用在欺诈与真实案例下采用欠采样 40:60 训练的 C4.5 DT 模型，实现了 $$ 165,000$ 的成本节约和 $\%$ 的准确率，比提出的堆叠装袋方法少了 $\%$ 。令人惊讶的是，一些 MLP 模型节约的金额很少，最差的一个甚至导致了 $$ 6,000$ 的损失，尽管其准确率为 $\%$ （Phua等人，2004年）。在成本节约和模型准确率之间观察到了反向关系，这归因于增加误报警数量的成本以便更多地检测到欺诈案例。因此，在这种情况下，利用更重要的度量标准的重要性是显而易见的。

堆叠装袋模型考虑了对原始数据集进行不同分区训练的 33 个分类器。从这些分类器中，只有排名前 15 的分类器被装袋以产生最佳预测结果，其中九个是 C4.5 模型，四个是 MLP，两个是 NB 分类器。研究中确定的一个局限性是成本的简单性和数据集的规模较小，作者建议探索 SMOTE，因为已经证明它能更好地处理不平衡数据问题（Phua等人，2004年）。更多数据集的可用性也将允许验证这些结果。

vi. 其他监督方法

Mahmoudi和Duman提出了修改的费舍尔判别分析（MFDA），这是线性判别分析（LDA）的一种改编，用于信用卡欺诈检测系统（Mahmoudi & Duman，2015年）。LDA 是一种监督学习方法，已被用于降维，并且甚至被应用于通过确定输入向量的线性函数之间的决策边界或表面来对数据进行分类。MDFA 通过在两个类别上应用加权平均来调整 LDA 模型中的费舍尔准则，定义权重为每张卡可用的总授信额度（Mahmoudi & Duman，2015年）。这种加权使线性判别向着更有经济效益的准确检测案例的方向偏置，而不仅仅是最大化正确分类的实例数量。因此，MDFA 不是最大化正确分类的实例数量，而是尽可能确保关键和具有成本效益的实例被正确分类（Mahmoudi & Duman，2015年）。

作者对提出的 MDFA 进行了实验，将其与 DT、MLP、NB 和标准 LDA 模型的性能进行了比较。研究中使用了土耳其一家银行提供的数据集，该数据集包含 8,448 笔合法交易和 939 笔欺诈交易，共计 102 个特征。通过使用 DT 模型进行特征选择，使用选定的特征来训练其他模型。数据集被分为三部分进行交叉验证。

文献对模型结果的评估侧重于经济方面，而不是观察实际预测准确性或性能。作者使用成本模型而不是观察流行的分类器性能指标（如召回率、精确率或整体准确率）来确定每个模型实现的成本节约百分比（Mahmoudi & Duman，2015年）。此外，文中仅考虑了每个模型前 313 个排名最高的欺诈预测。

结果显示，提出的 MDFA 实现了最大的整体节约增长，达到了 $\%$ ，正确分类了 313 个中的 236 个，或者所有样本的 $\%$ （Mahmoudi & Duman，2015年）。MLP 显示了所有模型中最差的成本节约，仍然有显著的增长，达到了 $\%$ ，将 $\%$ 的欺诈交易正确分类为欺诈。LDA 正确检测了 $\%$ 的欺诈案例，比提出的 MDFA 多。然而，与 MDFA 相比，LDA 在成本节约方面差了近 $\%$ ，节约增长为 $\%$ 。总的来说，作者认为研究结果和提出的模型是有利的，并将未来的努力直接投向研究其他类型的线性判别函数，如线性感知器判别（LPD），以开发迭代线性判别函数（Mahmoudi & Duman，2015年）。此外，考虑真实样本的误分类成本可能是可变的，而不是固定的，限制误报警数量和消费者的不满，这可能导致可变的流失成本（Mahmoudi & Duman，2015年）。

Dhieb等人提出了用于欺诈汽车保险索赔的检测系统，提出了极端梯度提升（XGBoost）与 DT 的结合（Dhieb，Ghazzai，Besbes，& Massoud，2020年）。XGBoost 是由陈和Guestrin（2016年）提出的系统，专门设计用于优化内存使用，并利用现代硬件的计算能力，从而提高执行速度和性能（Dhieb等人，2020年）。在提出的方法中，使用增强学习从原始 DT 构建顺序子树，其中每个子树减少前一个子树的错误。这导致了成本函数的残差的更新和错误的减少。

文献中提出的 XGBoost DT 模型与标准 DT、NB 分类器和 $k NN$ 进行了评估。使用的数据集包含 64,000 多笔汽车保险索赔，作者未提及欺诈与合法案例的比例或类别是否平衡。此外，除了简要讨论处理错误或缺失值的一些次要预处理步骤外，文中未提供任何关于特征选择或提取技术或步骤的见解。然而，作者制作了一个混淆矩阵，显示了数据集中每个特征之间的相关性。在训练和测试之后，实验结果显示，提出的检测系统在除训练时间外的所有指标上得分最高（Dhieb等人，2020年）。这包括准确率为 $\%$ ，精确率为 $\%$ ，召回率为 $\%$ ，F-分数为 $\%$ 。 $\mathrm{NN}$ 算法表现最差，F-分数为 0.255（Dhieb等人，2020年）。DT 模型是第二好的模型，F-分数为 89.2%；然而，它在计算效率方面超过了 XGBoost，训练时间为 $\mathrm{~s}$ ，少于 XGBoost 的 $\mathrm{~s}$ 的一半（Dhieb等人，2020年）。NB 分类器的表现也很差，F-分数为 $\%$ ，因此，作者得出结论，支持他们提出的模型。

5.2. 无监督方法

i. 隔离森林（IF）

2008年，Liu等人提出了一种名为 IF 的新型无监督异常检测方法，旨在探索明确隔离异常的概念（Liu，Ting，& Zhou，2008年）。根据作者的说法，隔离的概念在当前文献中尚未被研究，使该方法能够利用子采样创建具有低常数线性时间复杂度和低内存需求的算法（Liu，Ting，& Zhou，2008年）。IF 还能够扩展以处理大规模数据集和具有许多无关特征的高维问题。

隔离样本涉及构建隔离树（iTrees）的集合，以将其与其他样本分离开来（Liu，Ting，& Zhou，2008年）。通过选择随机特征生成分区，然后任意确定该特征最大值和最小值之间的分割值来生成分区。这种分区是递归进行的，可以用 iTree 结构表示，隔离一个点所需的分区数量等于从根节点到终止节点的路径长度（Liu，Ting，& Zhou，2008年）。假设异常很容易隔离并且需要更少的分区。相反，正常观察很难隔离并且需要更多的分区。
近年来，将IF算法应用于信用卡欺诈检测的努力才刚刚兴起。2018年，Ounacer等人提出了使用IF算法来检测信用卡欺诈交易的方法。作者旨在解决监督学习中的问题，并展示了实时环境中高准确性和检测性能。该过程的训练阶段涉及使用训练集的子样本构建IF模型，测试阶段则通过模型传递每个样本，计算跨所有树所需的分割次数以隔离该观察结果，并返回介于0和1之间的异常分数，其中1表示欺诈，阈值设置为0.5来对样本进行分类。该方法与其他无监督模型（如OCSVM、LOF和 $k$ -means聚类）进行了比较，使用了包含284,807笔交易的欧洲信用卡数据集，其中仅有492笔欺诈交易。出于隐私原因，除时间和金额外，所有输入特征均使用PCA进行转换，模型使用的特征包括获得的28个主成分。结果显示，IF表现出最佳性能，准确率和AUC分别为 $\%$ 和 $\%$ 。排名第二的是 $k$ -means聚类算法，准确率和AUC分别为 $\%$ 和 $\%$ 。作者总结强调了IF算法在检测欺诈交易方面的能力，并建议探索将该模型用于在线大数据处理架构的实现。

根据Stripling等人的报道，有69%的行业专家认为工伤赔偿欺诈有增加的趋势。工伤赔偿保险政策涵盖了员工在工作期间遭受伤害或疾病时产生的费用。作者提出使用一个模型，利用IF算法从训练集的特征计算异常分数以创建一个新特征。对于每个样本计算的异常分数被增加到一个新的训练集中，用于训练分类器，旨在提高其性能。根据文献，应用IF转换的名义属性的选择由专业人员知识驱动，以获得有意义的分数。

Stripling等人在他们的工作中对一个来自欧洲某匿名组织的真实工伤索赔数据集的性能进行了实证评估。该数据集包含9,572个带标签的样本，具有23个特征，由于保密原因，只有3个特征被描述：受伤类型、保单持有人的行业部门和伤残登记时长。用于比较的一些分类器模型包括LR、DT、RF、线性核SVM和径向基函数核SVM。每个模型的AUC分数与使用IF计算的异常分数和不使用进行了比较。线性SVM在不使用异常分数时取得了最高的AUC，为 $\%$ ，而使用IF异常分数时为 $\%$ 。所有模型在使用IF异常分数时的AUC都减少了约3-5%。然而，作者指出这并不一定是唯一需要考虑的标准。当模型的结果呈现给提供数据集的公司的调查员时，他们发现调查员更加赞赏，因为模型揭示了以前未被人类专家发现的欺诈索赔。调查员确认该模型表现出高检测准确性和实用性，特别是对以前未被发现的案例。

作者总结强调了该模型的好处，尤其是因为它以无监督方式工作。这在标签可能难以获得或成本高昂的情况下尤为有用。未来改进模型的建议包括探索自动化特征选择过程的技术。模型的可扩展性也是进一步研究和研究的一个方向。

ii. 自组织映射 (Self-Organizing Maps，SOM)

自组织映射 (SOM) 是一种利用无监督学习的神经网络，根据输入数据的拓扑结构配置网络的神经元 (Kohonen, 1990)。这个过程被称为自组织，通过迭代调节神经元的权重来逼近输入数据，从而对数据集进行聚类和描述 (Quah & Sriganesh, 2008; Kohonen, 1990)。SOM 中的神经元按照矩阵结构排列，将来自高维空间的输入映射到二维神经元阵列中 (Quah & Sriganesh, 2008)。这种映射旨在将相似的输入向量建模为在结果矩阵中更接近的神经元，提供了输入的可视化。

在迭代训练过程中，可以使用各种距离度量来对节点进行分组，例如欧氏距离、曼哈顿距离、切比雪夫距离等 (Zaslavsky & Strizhak, 2006)。训练后，数据集中的数据通过自组织分类为合法或欺诈集，之后任何新交易也会在传入 SOM 之前经过同样的处理。这些新交易会根据是否在特定阈值内被分类为合法或欺诈 (Quah & Sriganesh, 2008)。与仅具有欺诈和合法标签的二元分类不同，SOM 方法还可以有多个代表每个类的聚类。

Zaslavsky 和 Strizhak 首次提出了将 SOM 作为检测信用卡欺诈交易的技术 (Zaslavsky & Strizhak, 2006)。作者应用 SOM 来创建持卡人典型行为模型，分析偏差以识别可疑交易。文献中的初始步骤是创建持卡人概要，这是一个代表持卡人历史上执行的交易的一般模式的模型。这个模型是根据交易集合由 SOM 训练的，可以识别持卡人的典型交易 (Zaslavsky & Strizhak, 2006)。作者在多种行为特征的持卡人记录上检查了 SOM 模型的性能，以探索构建模型与交易相似度的依赖关系。作者表明，该方法的准确性随着数据集大小的增加而增加，特别是在检查更不平衡的信用卡时 (Zaslavsky & Strizhak, 2006)。
此外，作者构建了二维地图来说明持卡人行为的聚类，该地图中的群集由三种类型定义：典型的 ATM 交易、典型的销售点 (POS) 交易和罕见或异常交易。文献中关于方法的定量性能讨论有限；然而，文献中的方法被认为处于研究的早期阶段。所提出方法的优势在于不依赖于数据分布的统计假设，并且能够很好地处理嘈杂的数据。此外，该模型允许随着新交易的涌入修改模型，除了持卡人执行的一系列交易外，不需要任何先验信息 (Zaslavsky & Strizhak, 2006)。

Quah 和 Sriganesh 还提出使用自组织映射神经网络 (SOMs) 作为一种技术来帮助检测欺诈，通过利用它们来揭示数据中各种特征或属性之间的隐藏模式 (Quah & Sriganesh, 2008)。此外，作者将 SOM 用作预分类器，一种在实时检测系统中减少需要发送进行审核的交易数量的手段，从而降低处理时间、成本和复杂性 (Quah & Sriganesh, 2008)。提出的 SOM 模型输出从输入向量中解读出的簇，勾勒出每个持卡人的个人资料，推导出支出和行为模式。数据集中的交易与持卡人的个人资料进行比较，并基于它们与该簇的欧氏距离进行聚类。在将样本分组到适当的簇后，会指定一个控制围绕质心的半径的参数，以设定和控制将交易标记为在该簇内或不在其中的阈值 (Quah & Sriganesh, 2008)。对于特定持卡人，密集的可能表明他的许多交易属于一种特定类型，而稀疏的簇可能意味着另一种特定类型的交易很少 (Quah & Sriganesh, 2008)。因此，在确定的阈值范围内的密集簇中的交易会被过滤掉，这有助于系统更容易地识别需要进一步审核的交易 (Quah & Sriganesh, 2008)。

该模型使用新加坡一家银行的数据集进行了实现。然而，根据作者的说法，所进行的研究还处于早期阶段，就像 Zaslavsky 和 Strizhak 在 (Zaslavsky & Strizhak, 2006) 中提出的 SOM 一样。作者的工作仅演示了该方法的聚类能力，使用可视化表示形成的簇以及检查同一簇中特征的相似性。讨论了通过实现前馈 \mathrm{NN}NN 来进一步扩展提出的研究，使用提出的 SOM 模型的输出作为训练输入 (Quah & Sriganesh, 2008)。我们注意到文献中对模型过滤准确性的结果或度量的数据较少。尽管如此，作者提到，当该算法实施并在银行架构中进行试验时，执行非常迅速，执行时间不到一分钟 (Quah & Sriganesh, 2008)。作者指出提出的模型的局限性包括其对超参数选择的敏感性，如神经元数量、所使用的相似性度量以及簇中心的选择 (Quah & Sriganesh, 2008)。

延续先前文献的工作，Olszewski在一个实际的欺诈检测系统中实施了SOM模型，该模型基于一种阈值型二元分类算法（Olszewski, 2014）。首先，用户账户由汇编一系列记录的数据矩阵表示。然后，使用SOM可视化用户账户的特征，并计算在网格上可视化特征的质心。这导致一个可以可视化整个账户的二维点。文章中使用的分类方法在图6中以图形方式呈现，该图显示了基于SOM网格的单个账户（Olszewski, 2014）。

根据整个SOM网格的质心（如图6所示）与对应于U-矩阵中最大值的SOM神经元之间的不相似度值来设置分类阈值（Olszewski, 2014）。U-矩阵是SOM的图形表示，其中每个条目对应于SOM网格中的一个神经元。每个条目的值是神经元与相邻神经元之间的平均不相似度（Olszewski, 2014）。因此，U-矩阵中的一系列高值代表了在SOM网格上分隔数据簇的边界线（Olszewski, 2014）。

Olszewski在一个包含来自波兰的10000名信用卡持卡人账户的信用卡欺诈数据集上评估了所提出的模型（Olszewski, 2014）。仅使用了三个特征：交易中的金额、交易地点和交易时间。在所有账户中，只有100个是欺诈性的，占总数据集的1%。该模型的检测性能与基于标准SOM的聚类模型、基于高斯混合（GM）的模型以及由Huang等人在（Huang, Tsaih, & Yu, 2014）中提出的增长式分层SOM（GHSOM）进行了比较。GHSOM方法是为了发现欺诈性财务报告的拓扑模式，作者还提出了分类规则。GHSOM的不同之处在于主要侧重于创建数据簇，而不是利用SOM可视化（Olszewski, 2014; Huang等人，2014）。

实验结果显示，所提出的基于SOM的模型在所有模型中表现最佳，通过检测阈值实现了完美的分类，精确度、召回率、准确度和F分数均达到100%的完美分数（Olszewski, 2014）。基于SOM聚类的方法取得了最接近的结果，F分数为86.12%，召回率为90%，准确度为85.5%，精确度为82.57%。基于GHSOM的方法和基于GMM的方法的F分数分别为80%和69.77%。因此，作者得出结论，根据实验结果，所提出的SOM模型配合检测阈值在三种其他模型上展现出明显的优势。该模型具有完美的欺诈检测率，没有误报。作者建议探索其他检测方法，以观察模型的灵活性并将其应用于其他领域（Olszewski, 2014）。我们强调这些结果的重要性，因为在我们调研的任何其他文献中，我们都没有观察到信用卡欺诈领域的完美检测率。

iii. 自编码器

自编码器（AE）是一种对称结构的无监督深度学习网络，中间层节点较少。它包括一个将输入编码为低维表示的部分，以及另一个部分，将该输入解码或重新构建（Boukerche等，2020）。训练AE的目标是高效地学习数据的减少编码，然后进行重构。如图7所示，输入层将输入数据传递到隐藏层，其中学习低维编码。然后，编码从隐藏层传递到输出层，其中进行解码并尽可能地重构。AE中隐藏层的数量是任意的，条件是对于网络的每个部分，例如编码器，每个后续隐藏层的神经元数量必须少于前一层。这种架构在网络中施加了一个瓶颈，限制了可以通过的信息量，从而迫使对原始输入进行压缩的知识（Kucharski, Kłeczek, Jaworek-Korjakowska, Dyduch, & Gorgon, 2020）。

使用AE检测异常的前提是，异常比正常实例更难由经过训练的AE重构。因此，可以使用AE为数据集的每个样本确定重构误差，随后可以将其用作异常分数（Boukerche等，2020；Chalapathy & Chawla, 2019）。自编码器的几种正则化类型已经在最近的文献中引入，能够学习更丰富和更具表现力的输入特征表示。其中一种例子是稀疏自编码器（SAE），它通过在训练期间保持层中神经元的前K个活跃单元来鼓励层中的稀疏性（Makhzani & Frey, 2014）。去噪自编码器（DAE）被训练以从其损坏版本的“修复”输入中重构输入，首先通过随机映射损坏初始输入来完成此操作（Vincent, Larochelle, Lajoie, Bengio, & Manzagol, 2010）。收缩自编码器（CAE）通过学习对周围实例的小变化具有鲁棒特征表示，通过将编码器激活的Jacobian矩阵的Frobenius范数作为惩罚项（Rifai, Vincent, Muller, Glorot, & Bengio, 2011）。变分自编码器（VAE）通过在表示空间中引入正则化来防止过拟合，使用先验分布对潜在空间中的数据样本进行编码（Pang等，2020；Doersch, 2016）。此外，VAE使用重构概率而不是重构误差，这是从近似后验分布中抽取的潜在变量生成数据点的概率（An & Cho, 2015）。有关基于自编码器的欺诈检测方法摘要，请参阅表11。

图 7: 自编码器网络基本对称架构示意图。

Kazemi和Zarrabi提出使用自编码器在系统中检测和防止在处理之前的欺诈信用卡交易（Kazemi & Zarrabi, 2017）。作者建议训练一个AE来提取最相关的特征，然后添加一个softmax层来对网络的输出进行分类。文献通过比较具有不同配置的两个AE的结果来研究层大小的影响。第一个AE在输入层有20个神经元，然后在网络的第一个对称半部分的下一个隐藏层中有15、10和5个神经元。第二个AE在输入层有20个神经元，在随后的层中有30、50和100个神经元。两个AE模型在德国信用卡数据集上与SOM进行了比较，该数据集包含1000个样本。然而，文献没有提及用于重构误差的距离度量，文献的定性结果有限，但显示出具有更广泛架构的AE具有最佳的预测性能，准确率为84.1%。然而，SOM在准确率为82.4%的情况下，比具有较小隐藏层的AE表现更好，超出了0.8%（Kazemi & Zarrabi, 2017）。

表11

基于自编码器的欺诈检测的已发表文献摘要。

年份	参考文献	欺诈类型	方法	注释
2017	Kazemi和Zarrabi（Kazemi & Zarrabi, 2017）	信用卡	AE	AE准确率为81.6%，被SOM的82.4%的准确率超越
2018	Pumsirirat和Yan（Pumsirirat & Yan, 2018）	信用卡	AE	AE优于RBM，但在小数据集大小下表现不佳
2018	Sweers等人（Sweers, Heskes, & Krijthe, 2018）	信用卡	VAE	具有更深架构的AE在召回率方面表现最佳，为93.8%，与VAE相比，两种模型的精确度相同。
2018	Renström和Holmsten（Holmsten, 2018）	信用卡	堆叠AE	堆叠AE和VAE模型在召回率为99%的情况下优于单个AE模型，但精确度略低。
2019	Jiang等人（Zou, 2019）	信用卡	DAE-MLP $^{\mathrm{a}}$	使用DAE从输入中去除噪声，并使用输出来训练MLP分类器。优于在原始输入上训练的MLP分类器。
2020	Misra等人（Misra et al., 2020）	信用卡	AE-MLP $}^{\mathrm{a}}$	仅使用编码器进行特征提取的AE，使用输出来训练分类器。AE-MLP分类器优于2018年Pumsirirat和Yan的AE。
2016	Paula 等人（ Paula, Ladeira, Marzagão, 2016）	洗钱	$\mathrm{AE}$	AE 能够检测出领域专家先前鉴定的欺诈案例 [^2]。

Pumsirirat 和 Yan 进行了一项更全面的研究，提出使用 AE 在与先前提到的研究相同的数据集以及另外两个数据集中检测欺诈（Pumsirirat & Yan, 2018）。还使用了一个澳大利亚数据集，包含 690 个样本，以及一个熟悉的欧洲信用卡数据集，包含 284,807 个样本。与先前文献不同，本研究中的数据集经过了 PCA 预处理和转换。AE 设计为 21 个输入神经元，网络编码器部分的每一层分别有 16、8 和 4 个神经元，采用双曲正切激活函数，均方误差（MSE）被用作重构误差的度量（Pumsirirat & Yan, 2018）。受限玻尔兹曼机（RBM）是一种能够学习其输入概率分布的浅层网络，也被用于比较。结果显示，两种方法在德国数据集上表现不佳，AE 的 AUC 为 43.76%，略低于 RBM 的 $\%$ 。澳大利亚数据集的表现并未有太大改善；然而，在这里 AE 表现更好，AUC 为 $\%$ ，而 RBM 为 $\%$ 。在三个数据集中最大的欧洲数据集上，两种模型的 AUC 显著提升。AE 表现出优越性，达到 $\%$ ，而 RBM 为 $\%$ 。因此，对于大型数据集，作者得出结论，AE 和 RBM 模型均表现出在检测大型数据集中的欺诈信用卡交易任务中的出色能力（Pumsirirat & Yan, 2018）。

Sweers 等人通过提出 VAE 模型来扩展先前的文献，以检测欧洲信用卡数据集上的欺诈交易，并将其性能与常规 AE 进行比较（Sweers, Heskes, & Krijthe, 2018）。同样，数据集经过 PCA 转换以降低维度并隐藏私人信息，引用了保密方面的担忧。作者实现了四种 AE 和四种 VAE 结构，结构复杂性不同。前两个 AE 和 VAE 模型具有一个包含 2 或 10 个神经元的隐藏层。每种类型的 AE 的后两个模型具有多个隐藏层“堆叠”，每层神经元数量不同，因此被称为堆叠 AE 和堆叠 VAE 模型。使用概率 VAE 编码器对输入进行编码后，得到后验分布，然后计算重构概率。从正态分布中抽取样本，使用后验分布的均值和标准差重新参数化。然后通过概率 VAE 对样本进行解码，得到先验分布，其均值和标准差用于计算重构概率（Sweers, Heskes, & Krijthe, 2018）。结果显示，具有更大隐藏层的堆叠 AE 模型在召回率方面表现最佳，为 $\%$ ，而堆叠 VAE 为 $\%$ （Sweers, Heskes, & Krijthe, 2018）。两种模型的精确度相同，为 0.009，这似乎非常低，表明模型产生了许多误报警，但作者并未对此进行讨论。然而，堆叠 VAE 显示出优于简单 AE 和简单 VAE 结构的性能。文献指出，两种模型在检测信用卡数据中的欺诈交易方面表现相对类似，但我们认为在得出这样的结论之前，对模型精确度进行更深入的讨论仍然是必要的。

Misra 等人最近的工作（Misra, Thakur, Ghosh, & Saha, 2020）采用了 Pumsirirat 和 Yan（Pumsirirat & Yan, 2018）提出的方法，但在方法上略有变化。作者首先使用经过 PCA 转换的特征集训练 $\mathrm{AE}$ ，然后仅使用网络的编码部分提取数据的代表性特征（Misra et al., 2020）。接下来，使用监督方式在编码特征上训练分类器，使用交易标签。在测试时，测试集使用 $\mathrm{AE}$ 进行编码，然后传递给分类器进行分类。作者尝试了三种不同的模型，如 MLPs、 $k NN$ 和 LR，并发现 MLP 取得了最佳性能。该模型随后与（Pumsirirat & Yan, 2018）中的模型进行比较，表现出在检测信用卡欺诈方面整体更为有效，其 F 分数为 $\%$ ，准确率为 $\%$ ，而较差方法分别为 $\%$ 和 $\%$ 。作者得出结论，所提出的方法在精确度和召回率之间保持了一定的平衡，并建议在未来通过对交易批次进行训练来调整该技术以处理流数据。作者指出，然而，定期重新训练模型以跟上欺诈演变模式的重要但具有挑战性的任务。

Renström 和 Holmsten 提出了一种新颖的堆叠 AE 结构，以进一步发展先前的研究（Renström & Holmsten, 2018）。三个具有一个隐藏层的 AE 分别在串行配置中进行训练，前一个 AE 的输出和分类误差作为下一个 AE 的输入。所提出的模型使用重构误差中的 MSE 作为度量，并与单个 AE 和 VAE 在相同数据集上进行比较，采用相同的 PCA 特征转换方法（Renström & Holmsten, 2018）。结果显示，所提出的堆叠 AE 方法在召回率方面表现出 $\%$ 的提升，而单个 $\mathrm{AE}$ 为 $\%$ 。这种提高的召回率值表明只有 $\%$ 的欺诈交易未被检测出，而 VAE 显示出与堆叠 AE 类似的结果。单个 $\mathrm{AE}$ 的精确度为 $\%$ ，高于所提出的堆叠 AE 的 $\%$ （Renström & Holmsten, 2018）。我们注意到，作者的研究结果和讨论比 Sweers 等人（Sweers, Heskes, & Krijthe, 2018）的工作更为详细和深入，主要通过提供模型达到的精确度数值来清晰呈现结果和讨论。

Tingfei 等人还提出了 VAE 用于信用卡欺诈检测任务；然而，作者建议将其用于解决不平衡数据问题，作为一种过采样方法，而不是对数据实例进行分类（Tingfei, Guangquan, & Kuihua, 2020）。VAE 用于生成并注入类似少数类的数据到训练集中。然后，使用具有一个隐藏层和 ReLU 激活函数的 MLP 在监督方式下对数据集进行训练。另外实施了另外两种用于过采样少数类的方法进行比较，使用与所提出方法相同的程序。第一种是合成少数类过采样技术（SMOTE），由 Chawla 等人提出，旨在通过沿着连接任意或所有 $k$ 个少数类最近邻的线段创建合成示例来解决分类任务中不平衡数据集的问题（Chawla et al., 2002）。与其通过替换进行过采样不同，SMOTE 创建沿线段的合成示例，连接任意或所有 $k$ 个少数类最近邻（Chawla et al., 2002）。另一种方法涉及使用 GANs 通过涉及两个竞争网络的对抗性来过采样少数类，这将在后续章节中进一步讨论。作者还使用欧洲信用卡数据集来实验模型，所有特征均经过 PCA 转换，除了购买金额和时间，它们被标准化和归一化到新的特征值，然后显示与转换特征的特征值相关（Tingfei et al., 2020）。

注入到模型中的少数类样本数量变化以研究对性能的影响。当注入模型的案例数量达到 175 时，模型的性能在所有五个指标上都有显著提高，并且所有三种模型均取得了最佳结果（Tingfei et al., 2020）。所提出的 VAE 方法的精确度、F 分数、特异度和准确率表现均优于其他技术。VAE 的准确率为 $\%$ ，比 SMOTE 和 GANs 的最佳值高出 $\%$ ，分别为 91%（Tingfei et al., 2020）。F 分数被认为是分类器性能的更好度量，对于所提出的 VAE 方法为 $\%$ ，而 GAN 和 SMOTE 技术分别为 $\%$ 和 $\%$ 。此外，通过调查发现，当注入到训练集中的案例数量达到实际少数类数量的 100 倍时，所有三种模型的性能都会显著下降，其中 VAE 受影响最小（Tingfei et al., 2020）。文献中假设，性能下降的原因可能归因于少数类的多样性差异。最后，还表明，尽管所提出的模型具有最佳召回率，但随着生成的少数类比例增加，其值几乎不受影响，并且差异最小（Tingfei et al., 2020）。
保拉等人提出使用在巴西外贸数据库上训练的自动编码器，旨在识别参与出口业务并显示与正常行为模式有偏差迹象的组织或公司（Paula, Ladeira, Carvalho, & Marzagão, 2016）。原始数据集包含80个特征，通过使用梯度提升机器，筛选出能够解释公司出口量变异性80%的18个特征。自动编码器网络设计为18个输入和输出神经元，以及一个6-3-6神经元结构的三个隐藏层作为瓶颈。通过简单观察，选择对网络进行50次迭代训练，以避免过度拟合或欠拟合，并在神经元中使用ReLU激活函数（Paula, Ladeira, Carvalho, & Marzagão, 2016）。该模型通过均方误差（MSE）进行评估，衡量估计值与实际估计之间的差异。MSE值按升序排列并绘制成图表进行视觉检查，结果显示最后20条记录中行为明显发生变化。作者提到这些样本已被转交给出口欺诈的第三方专家。专家认为该系统有效，并指出它识别出了专家已知的欺诈案例。因此，通过进一步研究，我们相信将这些新型深度学习架构应用于反洗钱系统将为未来的努力提供极好的机会。

iv. 其他无监督方法

念等人提出了一种用于检测汽车保险索赔欺诈的无监督谱排名方法（SRA），并将其应用于检测汽车保险索赔欺诈（Nian, Zhang, Tayal, Coleman, & Li, 2016）。在他们的工作中，作者扩展了谱聚类算法，展示了基于定义的拉普拉斯矩阵的谱优化可以被视为无监督支持向量机的松弛。通过使用拉普拉斯矩阵的特征向量的分量大小，可以近似支持最佳二元类别分离函数的程度。从中，可以产生异常分数而不是集群分组（Nian等，2016）。该技术将数据建模为一个无向图，其中顶点表示数据实例，邻接矩阵指定不同顶点之间的相似性（Nian等，2016）。

使用了公共汽车保险数据集，该数据集包含15,420个样本，欺诈率为6%，25个分类特征和6个数值特征，与其他文献中所见相同。标签被丢弃，仅在测试期间用于模型评估。该模型与设计用于相同检测任务的OCSVM和LOF进行了比较。评估的唯一定量性能指标是AUC，并且作者提供的讨论主要涵盖了使用不同类型核心的影响。尽管如此，所提出的SRA在三个模型中表现出最高的AUC为74%，而OCSVM为59%，LOF为69%（Nian等，2016）。结果还显示，模型的性能对使用的超参数敏感，因此需要仔细调整。此外，检查了由模型的主要特征向量形成的集群的视觉表示，以观察构建的分离结构的复杂性。我们注意到需要更全面地讨论各种其他相关性能指标；然而，所提出的SRA被证明适用于检测欺诈汽车保险索赔。

ARIMA模型是一种用于时间序列的技术，是自回归移动平均模型（ARMA）的泛化。ARMA模型由自回归（AR）模型和移动平均（MA）模型组成。AR模型假定观察值与特定数量的滞后或先前观察值以及误差项之间存在依赖线性关系。相反，MA模型利用观察值之间的依赖关系和应用于滞后观察值的残差误差（Moschini, Houssou, Bovay, & Robert-Nicoud, 2020）。

在时间序列分析中，中心假设是序列是平稳的，即均值为零，方差随时间恒定。然而，在大多数实际情况下，这通常不成立（Adhikari & Agrawal, 2013）。解决这个问题的方法是ARIMA模型，这是一种常见且简单的模型，可以使时间序列数据点进行差分处理，使其变得平稳（Moschini, Houssou, Bovay, & Robert-Nicoud, 2020；Adhikari & Agrawal, 2013）。在检测欺诈活动时，时间序列是一种有用的工具，用于处理通过聚合产生的聚合特征，聚合是一种从数据中导出新特征的方法，这些新特征可能对模型更有用（Pozzolo, Caelen, Le Borgne, Waterschoot, & Bontempi, 2014）。

Moschini等人最近在其研究中首次实施了使用ARIMA模型来检测信用卡欺诈交易。在他们的工作中，作者提出了该模型以解决现有数据集的不平衡性质以及许多模型缺乏考虑随时间变化的消费行为和模式的适应性。该模型是无监督的，模型的唯一信息来源是持卡人的消费行为。模型最初根据合法交易的每日数量进行校准，以了解客户的消费行为。然后，使用滚动时间窗口来预测测试集中的欺诈交易。欺诈交易基于其计算的标准分数（也称为Z分数）高于阈值而被标记（Moschini, Houssou, Bovay, & Robert-Nicoud, 2020）。

使用由防欺诈公司NetGuardians SA提供的数据集，其中包含24名持卡人从2017年6月至2019年2月的信用卡交易信息，实施了ARIMA模型，并与其他模型（如箱线图、LOF、IF和 $k$ -means聚类）进行了比较。作者评论数据集的高度不平衡性，其中欺诈比例仅占所有交易的0.76%（Moschini, Houssou, Bovay, & Robert-Nicoud, 2020）。实验结果显示，ARIMA模型显示出最高的精度和F分数，分别为50%和55.56%。然而， $k$ -means算法在召回率方面表现最佳。总体而言，LOF是最差的模型，精度为8.4%，F分数为14.04%；然而，作者指出该模型旨在与多维数据集一起使用，与本方法不同（Breunig, Kriegel, Ng, & Sander, 2000）。箱线图表现出最佳的整体性能，F分数为72.22%，尽管作者指出ARIMA模型的优势在于基于建模客户行为的概念。

总的来说，Moschini等人表明，ARIMA模型在同一天内存在大量欺诈活动时表现更好。与其他基准模型相比，它还减少了误报警报的数量，并通过使用滚动时间窗口考虑了客户的动态消费行为。作者确定的主要问题是ARIMA模型的假设是数据集中的观察值在时间上等间隔，而在本研究中，交易是不等间隔的。文献建议未来的研究工作将致力于使用更先进的方法，如连续时间自回归移动平均（CARMA）过程来解决这个问题（Moschini, Houssou, Bovay, & Robert-Nicoud, 2020）。

5.3. 半监督方法

i. 隐马尔可夫模型（HMM）

HMM是用于建模比传统马尔可夫模型更复杂过程的随机过程。它们由一组有限状态组成，受一组转移概率的控制。每个状态还有一个关联的概率分布，负责生成结果或观察。在HMM中，结果是已知的，但状态是未知或隐藏的（Rabiner, 1989）。

HMM的特征包括模型中的状态数量，对于每个状态，还有几个与模型系统的物理输出对应的不同结果或观察。状态概率矩阵或状态转移矩阵给出了从一个状态转移到另一个状态的概率，在单个步骤中，这可以通过状态转移图形式地表示，如图8所示。隐藏状态由 $x_{i}$ 表示，每个状态映射到一个观察结果 $y_{i}$ ，其概率为 $b_{i j}$ 。状态转移概率 $a_{i j}$ 表示从一个隐藏状态移动到另一个隐藏状态的概率（Toledo & Katz, 2009）。Rabiner在（Rabiner, 1989）中提供了关于HMM的全面教程。

Srivastava等人提出了一种信用卡欺诈检测系统。

隐藏状态

可观察结果

图8. 隐马尔可夫模型状态转移图示例。
一个模拟数据集被生成并用于训练和评估模型，作者指出了从不愿共享数据的机构获取数据的困难（Srivastava 等，2008）。不同长度的交易序列被生成并用于训练具有不同状态数量的 HMM。结果显示，随着序列长度和状态数量的增加，模型的分类性能也增加。然而，这也伴随着更高的计算复杂性成本。同样，模型表明随着序列长度的增加，误报率也增加。基于各种试验，作者最终选择了长度为100和5个状态的序列。通过改变夹杂在真实交易序列中的欺诈交易数量进行实验。结果显示，所提出的方法在性能上优于先前文献中提出的方法。HMM 在广泛变化的输入数据上平均达到了接近80% 的准确率，并且被证明可以扩展处理大量交易（Srivastava 等，2008）。研究强调了准确的消费模式的重要性，模型显示在信息质量低或缺乏信息的情况下性能明显下降。

Bhusari 和 Patil 也通过重新创建 Srivastava 等人提出的模型验证了 HMM 用于检测信用卡欺诈的性能，并在模拟数据集上取得了类似的结果（Bhusari & Patil，2016）。Dhok 的研究采用了类似的方法和方法，将 HMM 模型应用于真实的信用卡交易数据集（Dhok，2012）。结果与先前文献的结果一致，展示了 HMM 在该应用中的可行性和性能。Robinson 和 Aria 成功地将先前作者的工作扩展到预付信用卡处理和检测系统，以实时检测商家的欺诈行为（Robinson & Aria，2018）。

Lucas 等人提出了一种使用 HMM 模型进行信用卡欺诈检测的监督方法，通过创建描述持卡人交易之间时间依赖关系的序列特征（Lucas 等，2020）。作者建议使用 RF 分类器基于他们提出的 HMM 技术生成的序列特征来检测欺诈交易。文献框架中，信用卡交易序列从三个角度建模。

第一个角度涉及将交易序列的可能性与合法历史交易序列和至少包含一笔欺诈交易的序列进行比较。这两种比较都是必要的，因为欺诈行为不仅需要远离合法行为，还应该与风险行为相对接近（Lucas & Jurgovsky，2020）。其次，创建的特征描述持卡人和商家终端的交易序列，已被证明对提高检测效率有积极影响（Lucas 等，2020）。最后，作者考虑了两笔交易之间经过的时间和交易金额作为构建特征的主要信号。将这些角度结合起来，从训练集的数据中产生了八组序列，每个序列上都训练了一个 HMM（Lucas 等，2020）。每个 HMM 基于先前交易序列为交易分配一个可能性值。这些值被用作 RF 分类器的附加特征。

在文献中，作者提出的自动特征工程方法与使用不基于 HMM 特征的 RF 分类器在与行业合作伙伴的数据集上进行了比较（Lucas 等，2020）。实验表明，新方法在面对面交易和电子商务交易的精确度-召回率曲线的 AUC 增加了18.1%，对于电子商务交易增加了9.3%。还表明该方法的特征工程策略对于各种其他分类器可能是相关的，因为它对于特征构建的超参数选择具有鲁棒性（Lucas 等，2020）。作者建议的未来工作包括将 LSTM 网络的预测与基于 HMM 特征的 RF 分类器的预测相结合，以扩展 Jurgovsky 等人的工作（Jurgovsky 等，2018）。

ii. 生成对抗网络（GAN）

GAN 是由 Goodfellow 等人于2014年提出的一种深度学习框架，由两个相互竞争的网络组成（Goodfellow 等，2014）。第一个是生成模型 $G$ ，用于捕获训练数据的分布。它的对手是鉴别模型 $D$ ，确定样本来自训练数据的概率而不是 $G$ 。训练 $G$ 的目标是最大化诱导 $D$ （一个分类器）犯错，无法区分数据（Goodfellow 等，2014）。GAN 中的两个模型是深度学习架构，学习原始输入的表示。增加网络中的层数或层的大小可以帮助学习更深层次和更抽象的表示（Bengio, Courville, & Vincent，2013）。

如图9所示，生成模型的输入是随机噪声 $z$ ，然后通过一个函数进行转换，产生真实数据的示例。鉴别器通过最小化其预测错误来学习更好地区分真实和生成的示例，生成器则尝试最大化错误，导致形成一个在（6）中形式化为极小极大博弈的竞争：

$\min _{\theta_{G}} \max _{\theta_{D}}\left(\mathrm{E}_{x p_{d}}[\log D(x)]+\mathrm{E}_{z}[\log (1-D(G(z)))]\right)$

其中 $\theta_{G}$ 和 $\theta_{D}$ 分别是生成器和鉴别器网络的参数， $p_{d}$ 是数据分布， $p_{z}$ 是生成网络的先验分布（Goodfellow 等，2014）。尽管 GAN 是无监督学习算法，但在训练中使用了监督损失。迄今为止，在大多数金融欺诈应用中，GAN 被用作半监督方法的一种过采样数据增强方法，这也是本文将其分类为半监督的原因。

Mirza 和 Osindero 提出将 GAN 扩展为条件模型，称为条件 GAN（CGAN），通过在生成器和鉴别器上附加一些额外信息来对生成器和鉴别器进行条件化（Mirza & Osindero，2014）。这些额外信息可以是任何类型的信息，例如类标签或来自其他模态的数据，作为额外的输入层馈送到两个网络中。对 GAN 基础欺诈检测的调查工作概述如下：

表12

基于 GAN 的欺诈检测的已发表文献总结。

年份	参考文献	欺诈类型	方法	评论
2018	Chen 等人（Ali, 2018）	信用卡	SAE-GAN	GAN 基于 SAE 学习特征的训练，对多数类别有改进的 F 分数和精确度，但召回率下降。在 F 分数方面，SAE-GAN 优于 OCSVM 和 OCGP。
2019	Tanaka 和 Aranha（Aranha, 2019）	信用卡	GAN-DT	使用少数类别 GAN 基于过采样训练的 DT 具有稍高的精确度，但召回率低于使用 SMOTE 或 ADASYN 时。
2019	Fiore 等人（Fiore et al., 2019）	信用卡	GAN-MLP	使用 GAN 过采样训练的 MLP 具有改进的召回率，提出的模型在召回率方面也优于 SMOTE，但特异性略低。
2019	Ba（Ba, 2019）	信用卡	WCGAN-LR	使用 WCGAN 过采样训练的 LR 具有最平衡的性能，F 分数和 AUC 高于 GAN、CGAN、SMOTE 和 ADAYSN。然而，WCGAN 的召回率为64.2%，明显低于 ADAYSN 的90%。
2019	Zheng 等人（Zheng et al., 2019）	信用卡	AE-OCAN	基于 AE 学习的真实交易表示训练的互补 GAN 生成器；鉴别器被提出为 OCAN。提出的模型在 F 分数、精确度和准确度方面表现优于 OCSVM，但在召回率方面表现不及。
2020	Charitou 等人（Charitou et al., 2020）	洗钱	SAE-GAN	从整个训练集中提取的 SAE 特征，然后用于训练 GAN 的生成器生成互补样本。生成的样本被增加到训练集中，鉴别器被训练用于分类样本。提出的模型在 F 分数、准确度和精确度方面优于 LR、SVM、MLP 和 RF，无论是使用 ADASYN 还是 SMOTE。然而，RF 与 ADASYN 相比，在召回率方面表现更好。

[^3] 生成数据以用于分类器的训练集。表12 展示了涉及 GAN 用于欺诈检测的文献。
欧洲数据集被用于提出的方法的文献中进行训练和测试（Chen, Shen, & Ali, 2018）。训练集包括5,000个正常交易，对于测试则使用了492个欺诈和正常类别的交易。作者们使用了一种名为 t-分布随机邻居嵌入（t-SNE）的新颖技术来可视化高维数据，该技术由 van der Maaten 和 Hinton 在（van der Maaten & Hinton, 2008）中提出，以可视化测试数据的分布。进行了几项实验来证明所提出模型的有效性，其中第一项实验涉及改变 SAE 隐藏层大小以观察对整体模型预测性能的影响。当隐藏层的神经元数量从30变化到60时，隐藏层大小与模型精度之间呈现出明显的正向趋势（Chen, Shen, & Ali, 2018）。然而，当神经元数量超过50后，召回率和 F 分数开始下降。第二项实验涉及比较所提出模型与 OCSVM（由 Tax 和 Duin 在（Tax & Duin, 2001）中提出）等最先进的单类方法的性能，以及由 Kremmler 等人提出的单类高斯过程（OCGP）（Kremmler, Rodner, Wacker, & Denzler, 2013）。所提出的方法在三个模型中具有最高的 F 分数和精度，分别为 $\%$ 和 $\%$ ，OCGP 排名第二。然而，就召回率而言，OCSVM 表现最佳，为 $\%$ 。所提出的 SAE-GAN 以 $\%$ 的召回率排名第二，与 OCSVM 相比有显著的 $\%$ 差距。最后，对 GAN 的鉴别器进行了试验，有无 SAE 特征的情况下。所提出的技术证明了性能的提升，精度从 $\%$ 提高到 $\%$ ，F 分数从 $\%$ 上升到 $\%$ ，然而这种精度和 F 分数的提升略微降低了召回率，从没有 SAE 的模型的 $\%$ 下降到 $\%$ （Chen, Shen, & Ali, 2018）。

所提出的 SAE-GAN 模型的高精度被作者归因于模型是在正常交易上进行训练以更好地区分它们，因此不太可能错误分类正常交易（Chen, Shen, & Ali, 2018）。作者们认为所提出模型的低召回率是由于 SAE 输出的维度增加，导致数据过拟合，因为存在信息冗余（Chen, Shen, & Ali, 2018）。总体而言，文献表明，训练了 SAE 特征的所提出的 GAN 模型在检测信用卡欺诈方面优于独立的 GAN。然而，作者建议进一步研究以解决模型的稳定性和 F 分数收敛性差的问题，以提高其性能（Chen, Shen, & Ali, 2018）。

紧随其后，Tanaka 和 Aranha 开展了一项工作，旨在开发一种利用 GAN 在信用卡欺诈检测任务中提高分类器性能的方法（Tanaka & Aranha, 2019）。作者们使用 GAN 生成人工训练数据用于机器学习任务，这对于基于不平衡数据集的分类模型非常有用。与自适应合成采样（ADASYN）（He, Bai, Garcia, & Li, 2008）和 SMOTE（Chawla 等人，2002）等技术相比，GAN 生成人工数据的能力被比较。人工创建的数据的一个显著优点是，在处理包含敏感信息的数据时也非常有用（例如财务信息、医疗信息和图像）（Tanaka & Aranha, 2019）。在文献中，所提出的 GAN 生成器被训练以在输入噪声向量时模仿并生成少数类别的样本，鉴别器必须学会区分真实样本和生成器生成的假样本。因此，生成器将学会输出逐渐更像原始数据的样本。

在文献中，作者们使用欧洲数据集，实验过程如下概述（Tanaka & Aranha, 2019）：首先，目标少数类别（即欺诈交易）被分离，然后使用只有该数据子集的几个具有不同数量和大小隐藏层的 GAN 进行训练。两个 GAN 具有一个隐藏层，分别有128或256个神经元，另外两个 GAN 具有两个隐藏层，第一个和第二个隐藏层分别有128和256，或者256和512个神经元。神经元中的激活函数选择为泄漏整流线性单元（leaky ReLU）。使用 GAN 生成并增加新样本到数据集，直到平衡。使用平衡后的数据集训练了一个 DT 分类器。所提出的方法与使用 SMOTE、ADASYN 和没有任何过采样的其他 DT 模型进行了比较。最后，在平衡和不平衡的测试集上比较了模型的性能。

文献显示，所有模型在平衡测试集上的表现比不平衡测试集要好得多，作者提到这是合理的，因为分类器更容易识别少数类别标签（Tanaka & Aranha, 2019）。此外，对于所有使用过采样的方法，召回率至少提高了 $\%$ ，而简单的 DT 模型提高了 $\%$ 。SMOTE 和 ADASYN 的召回率最高，为 $\%$ ，具有较小两个隐藏层的 GAN 接近，召回率为 $\%$ 。然而，作者警告称，应更加重视不平衡测试集的结果，因为在实际应用中不能期望测试数据是平衡的（Tanaka & Aranha, 2019）。考虑到这一点，与 SMOTE 和 ADASYN 相比，GAN 达到了略微更好的准确率和精度，但召回率较差。这些指标的重要性取决于应用领域，在检测欺诈的情况下，高召回率被认为是至关重要的，因为它表示检测到的欺诈数量更多。因此，作者建议优先选择 ADASYN 和 SMOTE 而不是他们提出的方法（Tanaka & Aranha, 2019）。尽管如此，文献得出结论，通过进一步的工作和研究，可以合理地期望与其他两种技术相媲美的未来结果（Tanaka & Aranha, 2019）。

Fiore 等人进行了更广泛的研究，使用 GAN 对不平衡数据集中的少数类别进行过采样，以提高分类器的性能（Fiore 等人，2019）。作者选择的分类器是 MLP，并强调了实验设计和调整阶段的重要性。研究强调找到超参数的最佳值是最大化所提出方法性能的关键方面（Fiore 等人，2019）。因此，使用欧洲信用卡数据集，MLP 分类器在原始数据的三分之二的训练集上进行训练，以确定在测试集上表现最佳的超参数集。然后，所提出的 GAN 仅在欺诈样本上进行训练，并使用生成器生成的样本平衡原始数据。另一个 MLP 使用平衡并使用 GAN 生成的欺诈样本增强的数据进行训练，使用第一个训练的 MLP 的超参数。

为了开始网络的调整过程，作者比较了各种分类器的配置和结构。由于太多层会使训练复杂化并导致过拟合，而太少层可能会妨碍网络在良好抽象水平上构建表示，因此作为一个合理的折衷，作者选择测试只有两层或三层隐藏层的网络（Fiore 等人，2019）。隐藏层中的神经元数量是经验性地从20变化到40，除了生成器的第一层似乎需要更多单元（约100个）（Fiore 等人，2019）。探索了三种不同的激活函数，包括 Sigmoid、ReLU 和双曲正切函数。文献发现，表现最佳的分类器是一个具有两个隐藏层、30 个 ReLU 单元、30 个 Sigmoid 单元和两个 Softmax 单元的网络，用于输出最终分类。

文献显示，当生成的样本数量增加到训练集时，与不平衡训练集相比，召回率显著提高（Fiore 等人，2019）。召回率从不平衡数据集中的 $\%$ 提高到生成 3,150 个样本时的高达 $\%$ 。这种改进被一个微不足道的特异性下降所抵消，从 $\%$ 下降到 $\%$ ，对应着假阳性的增加（Fiore 等人，2019）。还进行了与 SMOTE 的比较，这一比较的重要性在于其与作者框架的相似性。所提出的 GAN 方法的召回率通常高于 SMOTE，而特异性高于作者的框架。然而，这种比较进一步证实了所提出的 GAN 的优越性能，其 F 分数最高为 $\%$ ，而 SMOTE 的 F 分数为 $\%$ （Fiore 等人，2019）。
Wasserstein GAN（WGAN）是由Arovsky等人提出的，它使用地球移动者（EM）距离作为误差度量，不需要像典型的GAN那样精心设计网络架构（Arjovsky，Chintala，& Bottou，2017）。Ba提出使用WGAN代替常规GAN，称其在训练中更稳定，能够在少数类上训练时产生更真实的欺诈交易（ $\mathrm{Ba}$ ，2019）。类似于Tanaka和Aranha在（Tanaka & Aranha，2019）中的工作，WGAN被用于过采样少数类并平衡数据集。然后使用这个数据集来提高LR分类器的性能。所提出的WGAN的架构仅包括一个隐藏层，并且网络的超参数（如学习率、丢失率和神经元数量）是使用随机搜索算法找到的。文献还将WGAN扩展为开发条件WGAN（WCGAN）以检查与WGAN相比的任何效果或性能改进。作者在方法论中使用了欧洲数据集，将模型训练在80%的欺诈样本上，每个小批次包含64个样本。Adam被用作优化算法，这是一种适用于数据和维度较大问题的随机优化方法（Kingma & Ba，2014）。所提出的WGAN和WCGAN的F分数与典型GAN和CGAN以及采样技术SMOTE和ADASYN进行了比较。结果表明，WCGAN是最平衡的分类器，其F分数为71%。然而，该模型的召回率为64.2%，相对较低，与ADASYN的召回率90.1%相比，尽管F分数较低，ADASYN似乎更有优势。然而，它的精度仅为1.8%，意味着它容易产生误报。WCGAN的AUC为94.8%，是所有模型中最高的。总的来说，可以得出结论，所提出的WCGAN产生了平衡的精度和召回率，导致了最佳的整体性能，具有最高的F分数（Ba，2019）。

郑等人提出了一种使用一类对抗网络（OCAN）来检测欺诈信用卡交易的方法，该方法使用了一个基于AE学习的数据表示的补充GAN（Zheng，Yuan，Wu，Li，& Lu，2019）。在文献中，AE负责从原始特征中学习合法交易的隐藏空间中的表示。然后，GAN使用一个生成器进行训练，该生成器在合法交易的低密度区域生成补充样本，而不是像常规GAN那样匹配表示的分布。图10展示了基于（Zheng等人，2019）的常规和补充GAN生成器输出之间的差异。随后，鉴别器被训练以基于概率分布阈值区分生成的补充样本和合法样本。由于欺诈行为是与真实行为互补的，预期该方法应能区分这两类（Zheng等人，2019）。

文献提出的方法的性能是使用欧洲数据集针对其他一类技术（如一类最近邻（OCNN）和OCSVM）进行评估的。还通过仅使用经PCA转换的原始特征对每个模型进行评估，探讨了使用AE学习数据表示的影响。使用包含700个合法交易的训练集和490个欺诈交易以及490个合法交易的测试集，郑等人提出的OCAN在所有其他模型中表现最佳，无论是精度、F分数还是准确性，并在召回率方面仅次于OCSVM（Zheng等人，2019）。所提出的方法实现的F分数为86.56%，比仅使用原始特征的OCAN高出2.4%。然而，仅使用原始特征的OCAN的精度更高，为97.55%，而提出的OCAN的精度为90.67%。在召回率方面，OCSVM更为有利，为95.09%，而具有学习表示的OCAN为83.2%。此外，相应ROC的AUC计算结果显示，提出的OCAN为97.5%，略高于仅使用原始特征的96.45%。总的来说，作者得出结论，与以往传统技术相比，所提出的方法在检测信用卡欺诈方面表现出色（Zheng等人，2019）。

Charitou等人提出了一种使用GAN的反洗钱系统，通过使用SAE从训练集中提取的稳健特征来训练模型（Charitou，Garcez，& Dragicevic，2020）。所提出的框架结构首先使用具有两个编码和两个解码层的SAE。SAE将输入投影到更高的维度，然后再从稀疏表示中重新构建。这种映射旨在增加正类和负类样本之间的距离（Charitou等人，2020）。接下来，从SAE提取的数据表示被用作GAN的输入，该GAN采用试图匹配数据表示并生成新的补充样本的补充生成器（Charitou等人，2020）。与真实数据表示一起，生成的样本然后用于训练鉴别器模型，学习区分和检测欺诈案例。

作者与英国一家公司合作，使用该公司提供的数据集来改进他们当前的系统。数据集包含4,700个样本，其中1,200个被标记为潜在的洗钱活动，占整个数据集的25%以上（Charitou等人，2020）。数据描述了该公司合法在线赌博服务的匿名化赌博活动，数据集中标记了已知欺诈或洗钱案例。关于数据的预处理或任何特征选择或提取步骤的具体信息未在研究中提及。所提出的模型的性能与LR、RF和MLP等各种其他模型进行了比较，使用了不同的采样技术，如SMOTE和ADASYN。所提出的SAE-GAN模型展示了最佳的整体性能，具有最高的F分数89.85%（Charitou等人，2020）。它还具有最高的记录准确性，为94.37%。具有ADASYN过采样的RF模型的召回率最高，为95.69%，而提出模型的召回率为93.08%，略低于88.62%的F分数（Charitou等人，2020）。基本的RF模型显示了最佳的精度，为87.81%，略高于SAE-GAN的86.72%。

总的来说，作者表示，与公司目前的反洗钱措施相比，该模型被认为是一项重大改进。所提出的SAE-GAN的F分数比当前系统提高了3.64%，比其他评估方法提高了0.52%（Charitou等人，2020）。该框架的多功能性在监督设置中得到进一步强调。建议尝试不同的稀疏编码方法可能会进一步改善模型的结果，作者将尝试将其实施到一个更广泛的框架中，用于未来设计用于生成合成数据的GAN的实验（Charitou等人，2020）。

iii. 其他半监督方法

Subudhi和Panigrahi提出了一种使用GA和无监督FCM聚类（GAFCM）来检测欺诈汽车保险索赔的新型混合方法（Subudhi & Panigrahi，2020）。本研究中提出的方法类似于Behera和Panigrahi在（Behera & Panigrahi，2015）中的研究中的方法，其中数据的大部分（真实）样本最初由FCM进行聚类，以识别并删除异常值，从而在与其余少数样本相结合时产生平衡的数据集。然后，在平衡的数据集上训练监督学习模型，进一步将样本分类为真实或欺诈类，并提高性能。

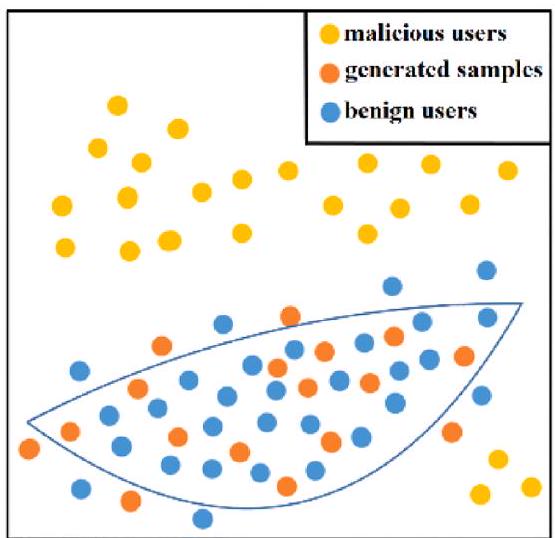
(a) 常规GAN

(b) 补充GAN

图 10: 两个生成器输出的示例，分别为 (a) 常规 GAN 和 (b) 互补 GAN。虚线蓝线表示良性交易的高密度区域。关于图例中颜色的解释，请参阅本文的网络版。

在这项研究中，作者通过使用遗传算法（GA）来优化 FCM 算法的聚类中心，在训练过程中观察检测性能的改进，并尝试使用汽车保险理赔数据而不是信用卡交易数据，从而扩展了 Behera 和 Panigrahi 的工作（Behera & Panigrahi, 2015）(Subudhi & Panigrahi, 2020)。所提出的方法被归类为半监督学习，是因为无监督的 FCM 仅使用大多数样本（即使未标记）进行异常检测。

文献中假设使用遗传算法训练 FCM 算法具有增强其稳健性的好处，使其能够对最佳聚类中心进行更广泛的搜索，并减少陷入局部最优解的可能性(Subudhi & Panigrahi, 2020)。使用包含15,420份汽车保险理赔数据集，其中仅有923份欺诈性理赔，占总理赔数的不到 6%。作者强调了这一领域研究者面临的重要问题之一，指出除了他们研究中使用的数据集外，公开数据集的可用性不足。其中四分之一的训练集用于测试，其余用于训练。对是否进行任何预处理或特征选择措施未进行讨论。在训练集中，将真实的大多数样本分离出来，并使用 10 折交叉验证对这些样本进行 FCM 训练。GAFCM 从原始的 10,627 个样本的训练集中移除了共 4,773 个真实实例(Subudhi & Panigrahi, 2020)。

采用平衡的训练集来训练两个后续的检测模型，一个是 FCM，另一个是 GAFCM，然后将它们与使用原始不平衡训练集训练的两个相同的 FCM 和 GAFCM 模型进行比较。当使用平衡的数据集时，两个模型的灵敏度、特异度和准确度均有明显提高。然而，总体而言，GAFCM 表现最佳，其灵敏度为 66.67 %，特异度为 86.95 %，准确度为 84.34 %（Subudhi & Panigrahi, 2020）。这些数值分别比使用不平衡数据集训练的 GAFCM 模型提高了 5.13 %、2.16 % 和 1.12 %。而使用不平衡数据集训练的 FCM 的灵敏度为 59.22 %，特异度为 84.49 %，准确度为 81.97 %，虽然明显比不平衡情况有所改善，但仍然不及提出的 GAFCM（Subudhi & Panigrahi, 2020）。

为进一步验证所提出的混合 GAFCM 技术相较于 Behera 和 Panigrahi 提出的 FCM 的性能改进，使用由每个模型生成的平衡数据集来训练一个监督学习器。分析了几个模型的性能，包括 DT、SVM 和 MLP。实验结果进一步确立了所提出的 GAFCM 技术的有效性，显示出在所有三个模型的所有指标上的全面改进（Subudhi & Panigrahi, 2020）。在使用 GAFCM 平衡数据集的三个模型中，SVM 显示出最高的灵敏度、特异度和准确度，分别为 $%、\88.45 % 和 \87.02 %。这些数值明显优于使用 FCM 异常检测的 SVM 模型的 \64.34 % 准确度、\72.23 % 特异度和 \70.15 %$ 准确度（Subudhi & Panigrahi, 2020）。因此，Subudhi 和 Panigrahi 提出的技术被认为比之前的方法更为有利，无论是作为独立分类器还是作为用于解决监督学习分类器中不平衡数据集问题的数据欠采样方法都表现更好。需要指出的是，建议进行更广泛的研究，以解决作者未涉及的某些方面，例如特征选择或预处理是否可能带来进一步的渐进性改进（Subudhi & Panigrahi, 2020）。

5.4. 基于图的方法

图形异常检测技术在欺诈检测领域的应用日益普及，特别是在分析大型网络中的连接模式可能会有所裨益的情况下。这些技术在反洗钱和保险欺诈检测领域尤为有用，这些领域通常涉及多个实体或组织可能涉及欺诈。Pourhabibi等人在2020年提供了一份最近和全面的基于图的欺诈检测技术综述（Pourhabibi et al., 2020）。然而，值得注意的是，需要重点强调一些与本调查直接相关的重要论文。

例如，Yang和Hwang提出了一个利用临床路径概念来检测医疗保险欺诈或滥用的过程挖掘框架（Yang & Hwang, 2006）。临床路径的应用旨在使医务人员按正确顺序执行护理服务，以便在不重复工作或浪费资源的情况下实现最佳实践。这些路径通常由医师的医嘱驱动，一旦创建，它们可以被视为要做出的决定和为给定患者提供的护理的算法（Yang & Hwang, 2006）。在他们的工作中，作者们概述了一个框架，涉及从临床实例中挖掘频繁模式，以促进自动和系统化地构建系统以检测医疗欺诈。该模型在真实数据集上进行了评估，实证结果表明该模型的效率及其在识别领域专家或手动构建的检测模型先前未识别的欺诈案例方面的能力（Yang & Hwang, 2006）。

Šubelj等人提出了一种利用社交网络分析来检测欺诈汽车保险索赔的专家系统（Šubelj et al., 2011）。在汽车保险欺诈案件中，有组织的合作者经常共同合作实施这些犯罪行为，这些合作者有时包括司机、按摩师、修理车库、技工、律师等（Šubelj et al., 2011）。因此，作者们将数据表示为网络，以观察不同个体或团体之间的关系。然后，通过采用一种称为迭代评估算法（IAA）的新型评估算法来实现对可疑实体或合作者的检测（Šubelj et al., 2011）。结果显示，所提出的系统能够高效地检测欺诈案例，并且适当的数据表示对实践中非常适用，因为它不需要标记的数据集（Šubelj et al., 2011）。该系统允许对领域专家的知识进行插补，因此可以根据新识别的欺诈类型进行调整。该系统的好处在于不需要大量数据，唯一的挑战在于它依赖于用户定义的阈值或必须进行调整的参数。

Branting等人探索了使用图分析来检测欺诈医疗保健索赔和活动（Branting, Reeder, Gold, & Champney, 2016）。作者应用各种网络算法组，其中一组算法计算了与可测活动（如医疗程序和药物处方）相关的已知欺诈和真实医疗保健提供者的行为相似性（Branting, Reeder, Gold, & Champney, 2016）。另一组算法估计了从医疗保健提供者到地理空间共同位置（如共享实践地点或其他地址）的风险传播（Branting, Reeder, Gold, & Champney, 2016）。所提出的模型在各种数据集上进行了实证评估，显示出高达 $\%$ 的F分数和 $\%$ 的AUC。还表明，基于位置共同风险传播算法的最具预测性特征（Branting, Reeder, Gold, & Champney, 2016）。

在反洗钱领域，Dreżewski等人提出了一种利用社交网络分析算法（SNA）来检测欺诈性汽车保险索赔的算法（Dreżewski, Sepielak, & Filipkowski, 2015）。在他们的论文中，作者指出，犯罪分子经常创建复杂的组织结构，可以识别这些结构。此外，可以检测网络中每个成员的角色，这都是通过SNA实现的。SNA模块通过为节点分配角色构建数据网络，然后分析节点之间的连接以找到实体之间的接近度，几乎像一个聚类算法（Dreżewski et al., 2015）。作者使用各种数据源，如银行对账单和国家法院登记，并比较两个不同领域网络中节点的角色分配。该分析揭示了关于欺诈真正领导者和网络内部成员角色的关键信息。使用节点接近度模块，提供了关于同一人拥有的不同银行账户的知识。通过使用该模块验证了分配给网络成员的角色的正确性，以找到在不同网络中具有相同角色的节点（Dreżewski et al., 2015）。总的来说，所提出的方法对于自动分析犯罪网络和识别犯罪团伙内部成员的角色分配模式非常有用（Dreżewski et al., 2015）。这种有效性在一定程度上归因于该模型利用多个数据领域。

Colladon和Remondi（Colladon & Remondi, 2017）还探讨了使用SNA不仅用于检测而且尝试预防洗钱。作者提出了一种新方法来对关系数据进行排序和映射，并基于某些网络指标，提出了一个预测模型来评估客户的风险概况。在他们的研究中，Colladon和Remondi将该模型应用于保理公司的中央数据库，该数据库包含与保理业务相关的财务操作信息以及有关公司客户的其他有用信息（Colladon & Remondi, 2017）。保理业务涉及企业或客户以折扣率将应收账款或发票出售给第三方，这可能出于许多原因，例如满足短期流动性需求。所提出的SNA模型用于预测与业务中涉及的每个客户相关的风险概况。分析集中在从债务人到保理方进行的经济交易和资金转移上。绘制了四种关系图：第一种考虑了与经济部门活动相关的操作风险；第二种考虑了与特定地理位置相关的风险；第三种研究了交易金额；第四种确定了不同组织之间存在潜在危险联系的链接（Colladon & Remondi, 2017）。这些图被过滤以关注与更高风险相关的交易，并且风险因素在分析中被分开以评估其重要性和贡献。

通过对图表的视觉分析，可以明显地识别出涉及法院审判的主体的清晰集群。基于此，建议设置警报，一旦集群中的任何节点涉及可疑或非法行为，即立即对所有节点进行检查。此外，对四种不同网络图的分析证明了研究网络内交易中心性的重要性，因为风险配置更高的客户通常在网络内处于较不中心的位置（Colladon & Remondi, 2017）。当将提出的模型应用于保理公司数据库时，已经证明其在预防洗钱方面是有效的和有用的。然而，作者们确定了一些需要未来研究解决的限制，其中一个限制是需要更大的样本量进行分析，以确定该模型在实践中是否具有普遍性（Colladon & Remondi, 2017）。另一个限制是值得研究额外未包含在这些研究中的控制变量的影响，例如参与金融交易的公司的年龄和规模（Colladon & Remondi, 2017）。最后，作者建议他们研究中提出的度量指标应与其他基于机器学习算法或甚至在国家层面上结合数据的工具相结合，以便更快地检测网络内可疑节点，旨在预防洗钱（Colladon & Remondi, 2017）。

6. 结论和建议

在这份调查中，我们概述并讨论了文献中异常检测问题的不同表述方式。我们统一了异常的概念，以提供对手头问题的清晰理论理解。本研究的方法论是基于这样一个使命，即全面审查异常检测技术应当使读者不仅了解使用特定模型背后的动机，还应当了解在应用于特定欺诈领域时它们的优势和局限性。我们通过详细比较分析了每种应用中实施的各种方法来实现这一点。

本文突出了检测欺诈及其对金融经济的有害影响的重要性，以及将异常检测技术应用于应对这一不断增长的问题所面临的挑战。本调查探讨的主要领域包括信用卡欺诈、保险欺诈和洗钱。显而易见，根据不同的欺诈应用，所面临的挑战有很大的不同。例如，系统实时检测欺诈对于信用卡欺诈至关重要，但在保险欺诈检测系统中可能并不那么重要。此外，我们表明，在本调查中概述的各种金融欺诈类型中，并不存在适用于所有不同类型金融欺诈的单一普遍适用的异常检测技术或方法。我们发现这一领域存在明显缺乏公开可用的数据集，无论是带标签还是不带标签，这被确定为该领域的一个重要限制。我们还将上述原因归因于对其他类型金融欺诈研究的不足。更重要的是，由于欺诈案例罕见，数据集的不平衡性被强调为在设计任何欺诈检测系统或模型时必须考虑的最关键因素之一。

从调查的文献中，明显可以看出一种趋势的明显转变，即大多数最近的研究采用了无监督和半监督模型，而不是监督模型。我们认为这是由于实践中带标签数据很难获得，因为手动标记的繁琐和成本较高。即使数据集已经标记，通常情况下也并非所有欺诈实例都被检测到。幸运的是，观察到无监督和半监督方法已经能够检测到以前未被领域专家或已有检测措施发现的欺诈。此外，在训练模型之前，越来越多的关注被给予开发复杂的特征选择和提取方法。这些做法已被证明通过减少计算复杂性和提高检测准确性来改善欺诈检测系统的有效性。

生成模型，即无监督方法，在本调查中被证明在最近的文献中特别受欢迎，并已应用于各种信用卡欺诈、保险欺诈甚至反洗钱的欺诈检测系统中。这些模型可以从训练集的潜在空间中学习原始特征的更深层次和更复杂的表示。GANs 和各种类型的不同 AE 网络是应用于这一领域的生成模型的例子。这些模型已被用作分类器，并且每个模型都展示了不同的优势，可以作为特征提取或过采样技术。例如，我们表明，由 AEs 从训练集中提取的特征显著提高了监督分类器（如 MLP）的性能。对于过采样少数类别，一种半监督方法解决了与本研究相关的不平衡类别问题，GANs 和 VAEs 已被证明在创建更真实的样本方面优于传统的过采样方法，如 SMOTE 和 ADASYN。这些方法也被证明优于涉及对多数类别进行欠采样的方法，例如随机欠采样、分层抽样甚至专门用于异常值检测和移除的聚类算法。

其他在近年来展示出有效性并越来越受欢迎的深度学习架构，特别是用于检测信用卡欺诈的 CNNs 和 LSTMs。CNNs 可以捕捉持卡人的短期时间关系和行为，并且与 MLP 相比，更不容易过拟合数据。另一方面，LSTMs 可以捕捉更长期的时间行为，并在与其他模型结合使用时识别出其他模型未能检测到的欺诈案例。这些类型的网络严重依赖于适当的特征转换策略，以将输入数据调整为这些类型模型熟悉的形式。由于这些转换，LSTMs 和 CNNs 将欺诈检测为上下文异常，这在这一领域被认为是最近的发展，因为大多数模型通常旨在检测点异常。

然而，深度学习模型的局限性在于，与 SVM 和 RF 等简单模型相比，它们需要比较仔细的设计和调整，因为它们对超参数选择和架构结构的选择相当敏感。此外，这些模型通常需要相对较高质量和数量的数据。由于深度学习模型通常以黑盒方式运行，到达其预测所涉及的过程可能需要复杂的工具和策略来帮助解释其可解释性。这些类型的网络还严重依赖于适当的特征转换策略，以将输入数据调整为这些类型模型熟悉的形式。此外，在设计阶段还必须考虑到用于优化这些模型的学习算法或损失度量的选择对其整体性能的影响。

最后，我们要关注欺诈检测模型的可解释性问题，这可以提供可解释的结果，有助于需要人类干预的应用或为支持决策提供有价值见解的推断。具体来说，从调查的文献中观察到，在这一问题上存在着显著的讨论不足，尤其是当它被认为是研究人员和行业在开发对他们提出的模型的运作方式有更深入理解或从数据中学习或发现模式的关键工具时。例如，当处理像 LR、DT、RF 和 NB 这样的简单模型时，这些模型本质上配备了机制，以概率地确定各个组件对整体模型的影响和证据。然而，这些模型已被证明在检测性能上不如更近期、更复杂的深度学习方法，这些方法通常是黑盒模型，因此最需要配备技术来帮助解释其结果。因此，我们认为在这方面未来研究存在几个机会，特别是针对两种在研究文献中显示出有望解释更复杂模型性能的具体模型：局部可解释的模型无关解释（LIME）（Ribeiro, Singh, & Guestrin, 2016）和 Shapley 加性解释（SHAP）（Lundberg, 2017）。

在我们看来，未来研究最有前景的方向涉及探究结合生成模型的过采样和判别能力以及 LSTMs 和 CNNs 捕捉数据中长期和短期时间关系的检测模型的性能，最终实现更强大和高效的欺诈检测系统。此外，基于这些发现，值得探索将本调查中探讨的技术应用于欺诈研究较少的领域，如证券与商品欺诈、抵押欺诈、内幕交易等。