【卡尔曼滤波】卡尔曼滤波器学习笔记 part 2

c_一土

已于 2024-10-30 17:32:11 修改

阅读量517

点赞数 8

文章标签：学习笔记

于 2024-10-30 17:30:00 首次发布

本文链接：https://blog.csdn.net/wjsabltys123/article/details/143307281

版权

date 2024-10-30

数学基础

数据融合（Data Fusion）

指的是将来自不同来源、不同格式或不同结构的数据集成到一个统一的数据模型或数据集中的过程。其目的是通过整合多样化的数据，提高数据的完整性、准确性和可用性。下面用一个例子来解释什么是数据融合。

当使用两个不同的秤来称量一个物体的重量，称量数据如下：

$Z_{1}=30g$ $\sigma _{1}=2g$

$Z_{2}=32g$ $\sigma _{2}=4g$

其中Z即为称得的重量， $\sigma$ 为标准差，两秤的称量结果满足正态分布。

根据正太分布的图像我们可以感觉出，真实值大概率在30g和32g之间，且更偏向于30g（称1的方差更小）。

这里根据已有的称重数据来估计真实值 $\hat{Z}$ ,这里采用卡尔曼公式进行估计：

$\hat{Z}=Z_{1}+K(Z_{2}-Z_{1})$

问题就转化为求出一个K值，使得估计值 $\hat{Z}$ 的标准差 $\sigma_{\hat{Z}}$ 最小，即方差Var( $\hat{Z}$ )最小。

Var( $\hat{Z}$ )=( $\sigma_{\hat{Z}}$ )^2= $Var(Z_{1}+K(Z_{2}-Z_{1}))$ = $Var((1-K)Z_{1}+KZ_{2})$ = $(1-K)^{2}Var(Z_{1})+K^{2}Var(Z_{2})$ = $(1-K)^{2}\sigma _{1}^{2}+K^{2}\sigma _{2}^{2}$

令Var( $\hat{Z}$ )最小,对上式求导，令其等于0得到

$K=\frac{\sigma _{1}^{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}=\frac{2^{2}}{2^{2}+4^{2}}=0.2$

此时融合后的标准差为

$\sigma _{\hat{Z}}=\sqrt{3.2}=1.79$

将K值代入计算得到估计真实值为

$\hat{Z}=30+0.2(32-30)=30.4$

如下图所示：

这个过程就叫做数据融合。

协方差矩阵（Covariance Matrix）

即是将方差和协方差在一个矩阵中表现出来，体现了变量间的联动关系。

例：

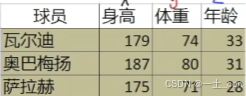
对三位球员的数据计算方差和协方差（身高设为x，体重设为y，年龄设为z）:

$\sigma _{x}^{2}=24.89$ $\sigma _{y}^{2}=14$ $\sigma _{z}^{2}=4.22$

$\sigma _{x}\sigma _{y}=18.7$ $\sigma _{x}\sigma _{z}=4.4$ $\sigma _{y}\sigma _{z}=3.3$

则其协方差矩阵为：

$P=\begin{bmatrix} \sigma _{x}^{2} &\sigma _{x}\sigma _{y} & \sigma _{x}\sigma _{z}\\ \sigma _{y}\sigma _{x}& \sigma _{y}^{2} &\sigma _{y}\sigma _{z} \\ \sigma _{z}\sigma _{x}& \sigma _{z}\sigma _{y} & \sigma _{z}^{2} \end{bmatrix}$

通过以下公式可以快速的算出协方差矩阵：

$a=\begin{bmatrix} x_{1} &y_{1}& z_{1}\\ x_{2}&y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}-\frac{1}{3}\begin{bmatrix} 1 & 1 &1 \\ 1& 1 &1 \\ 1&1 &1 \end{bmatrix}\begin{bmatrix} x_{1} &y_{1}& z_{1}\\ x_{2}&y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$

$P=\frac{1}{3}a^{T}a$

状态空间表达（State Space Representation）

从例子入手：

其动态方程表达式为：

$m\ddot{x}+B\dot{x}+kx=F$

这里我们定义F为输入u，并且定义状态变量 $x_{1}=x,x_{2}=\dot{x}$ ,，并且定义测量变量 $z_{1}=x,z_{2}=\dot{x}$ .则可以写出状态空间表达式：

因为实际情况中总是存在着各种不确定性，例如在以上系统中增加过程噪音和测量噪音。

在这种不确定的情况下，如何去估计一个较为精确的 $\hat{X^{k}}$ ，就要用到卡尔曼滤波器了。

卡尔曼增益/因数的引出

虽然噪声是不可测的，但是自然界中的噪音我们可以假设其符合正态分布。

即噪声的分布满足 $P(w)-(0,Q)$ ,其中0为期望，Q为协方差矩阵。那么如何计算噪声w的协方差矩阵Q呢？可以利用下面的公式计算Q：
$Q=E\begin{bmatrix} w &w^{T} \end{bmatrix}$

这里的E表示求期望。这里我们假设w中只有两个变量w1，w2，则结果为：

$Q=E\begin{bmatrix} \begin{bmatrix} w_{1}\\ w_{2} \end{bmatrix} &\begin{bmatrix} w_{1} & w_{2} \end{bmatrix} \end{bmatrix}=\begin{bmatrix} Ew_{1}^{} &Ew_{1}w_{1} \\ Ew_{2}w_{1}& Ew_{2}^{2} \end{bmatrix}=\begin{bmatrix} \sigma ^{2} _{w_{1}}&\sigma _{w_{1}} \sigma _{w_{2}}\\ \sigma _{w_{2}}\sigma _{w_{1}} & \sigma ^{2} _{w_{2}} \end{bmatrix}$