R语言结构方程模型代码与理解
引言
结构方程模型(Structural Equation Modeling,简称 SEM)是一种基于概率统计的多变量分析方法,可以用于探究变量间的因果关系。
SEM 可以同时估计测量模型和结构模型,从而可以考虑到测量误差和隐变量的影响。在 SEM 中,测量模型用来描述每个测量变量与其背后的潜在变量之间的关系,而结构模型用来描述潜在变量之间的因果关系。SEM 可以通过最大似然估计、贝叶斯估计等方法求解模型参数,从而得到模型的拟合度和参数估计结果。
总之,SEM是一种判断复杂变量之间的关系、贡献度、相关性的工具。(而不是一种回归模型)
小编以SEM为关键词检索,有很多所谓的“名师”课程,售价往往几千起步,成本非常高啊。

其实SEM本身并不是很复杂,小编总结了代码和原理,希望能运用到大家的实际研究中。
代码
实例1
其中,lavaan用于SEM分析,semPlot用于可视化路径结果,tidyverse用于数据处理
library(lavaan)
library(semPlot)
library(tidyverse)
示例1是一个lavaan包官方例子,https://www.cnblogs.com/squidGuang/p/9054301.html
首先加载数据
data <- HolzingerSwineford1939
data <- data %>% na.omit()
head(data, 10)

数据概念如下:
数据为整体为小学同学的智力测量因素
-
视觉因子(visual)对应x1,x2,x3
-
文本因子(textual)对应x4,x5,x6
-
速度因子(speed)对应x7,x8,x9

总共需要三个步骤:
-
根据数据的物理意义把模型的路径写出来 -
拟合SEM -
提取结果
#step 1:write the road of model
model <- ' visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9
mind =~ visual + textual + speed
'
#step 2: fit sem
fit <-sem(model, data = data)
#step 3: summary result
summary(fit, standardized = TRUE)
lavaan.version : '0.6.15' optim.method : 'nlminb' optim.converged : TRUE
estimator : 'ML' $estimator.args :
npar : 21 nrow.ceq.jac : 0 nrow.con.jac : 0 $con.jac.rank : 0
ngroups : 1 $nobs : 300
standard** = stat : 85.9448655188601 df : 24 pvalue : 6.68883060050973e-09
$pe : A data.frame: 25 × 11
lhs op rhs exo est se z pvalue std.lv std.all std.nox visual =~ x1 0 1.0000000 0.00000000 NA NA 0.9072288 0.7774612 0.7774612 visual =~ x2 0 0.5470812 0.09882671 5.535763 3.098769e-08 0.4963279 0.4215312 0.4215312 visual =~ x3 0 0.7213310 0.10796433 6.681197 2.369971e-11 0.6544123 0.5795833 0.5795833 textual =~ x4 0 1.0000000 0.00000000 NA NA 0.9912374 0.8518791 0.8518791 textual =~ x5 0 1.1104109 0.06542766 16.971581 0.000000e+00 1.1006808 0.8546353 0.8546353 textual =~ x6 0 0.9243902 0.05549562 16.656993 0.000000e+00 0.9162902 0.8374038 0.8374038 speed =~ x7 0 1.0000000 0.00000000 NA NA 0.6225275 0.5713785 0.5713785 speed =~ x8 0 1.1792097 0.16430796 7.176827 7.134293e-13 0.7340905 0.7273510 0.7273510 speed =~ x9 0 1.0757063 0.14979503 7.181188 6.910028e-13 0.6696568 0.6636308 0.6636308 mind =~ visual 0 1.0000000 0.00000000 NA NA 0.8759904 0.8759904 0.8759904 mind =~ textual 0 0.6541085 0.17227727 3.796836 1.465549e-04 0.5244309 0.5244309 0.5244309 mind =~ speed 0 0.4176643 0.11679979 3.575900 3.490256e-04 0.5331937 0.5331937 0.5331937 x1 ~~ x1 0 0.5386195 0.11472654 4.694811 2.668528e-06 0.5386195 0.3955541 0.3955541 x2 ~~ x2 0 1.1400248 0.10219508 11.155379 0.000000e+00 1.1400248 0.8223115 0.8223115 x3 ~~ x3 0 0.8466302 0.09058714 9.346030 0.000000e+00 0.8466302 0.6640833 0.6640833 x4 ~~ x4 0 0.3713885 0.04794545 7.746064 9.547918e-15 0.3713885 0.2743020 0.2743020 x5 ~~ x5 0 0.4471762 0.05854244 7.638496 2.198242e-14 0.4471762 0.2695985 0.2695985 x6 ~~ x6 0 0.3576937 0.04321801 8.276497 2.220446e-16 0.3576937 0.2987549 0.2987549 x7 ~~ x7 0 0.7995104 0.08159488 9.798537 0.000000e+00 0.7995104 0.6735266 0.6735266 x8 ~~ x8 0 0.4797287 0.07409492 6.474515 9.511703e-11 0.4797287 0.4709605 0.4709605 x9 ~~ x9 0 0.5698030 0.07081806 8.046012 8.881784e-16 0.5698030 0.5595942 0.5595942 visual ~~ visual 0 0.1914783 0.17533487 1.092072 2.748015e-01 0.2326408 0.2326408 0.2326408 textual ~~ textual 0 0.7123227 0.10778487 6.608744 3.875944e-11 0.7249722 0.7249722 0.7249722 speed ~~ speed 0 0.2773645 0.06962984 3.983414 6.793231e-05 0.7157045 0.7157045 0.7157045 mind ~~ mind 0 0.6315859 0.18759305 3.366787 7.604938e-04 1.0000000 1.0000000 1.0000000
上面是结果,接下来检验结果准确性,有以下指标
-
RMR 残差均方根 ,RMR 是样本方差和协方差减去对应估计的方差和协方差的平方和,再取平均值的平方根。一般RMR越小,拟合越好,理论上要小于0.08。 -
RMSEA 近似误差均方根,该值也是越小越好,RMSE理论上小于0.06,也可以放宽到0.08。 -
CFI 比较拟合指数,值在0-1之间。CFI 值越大越好,一般在0.9以上模型可接受 -
GFI 拟合优度指数,值在0-1之间,一般GFI 应该等于或大于0.90。 -
PGFI 简效拟合优度指数。它是简效比率(PRATIO,独立模式的自由度与内定模式的自由度的比率)乘以GFI。 PGFI 应该等于或大于0.90,越接近1越好。 -
PNFI 简效拟合优度指数,等于PRATIO乘以 NFI。 PNFI应该等于或大于0.90,越接近1越好。 -
NFI 规范拟合指数,变化范围在0和1间, 当为1的时候标识完全拟合。一般NFI 小于0.90 表示需要重新设置模型。越接近1越好。 -
TLI Tucker-Lewis 系数, 也叫做Bentler-Bonett 非规范拟合指数 (NNFI)。TLI接近1表示拟合良好。 -
Chisqare/df卡方值与自由度的比值,该值越小越好,一般要小于2,放宽到3也是可以接受的。
由于指标众多,也有很多取舍,但是常常使用的重要参考指标为:Chisqare/df,RMSEA ,CFI
fitMeasures(fit,c("chisq","df","pvalue","gfi","cfi","rmr","srmr","rmsea"))

最后作图:
semPaths(fit, #上面跑出来的数据模型
what = "std", #图中边的格式,#"path","std","est ","cons "
layout = "tree", #图的格式, tree circle spring tree2 circle2
fade=T, #褪色,按照相关度褪色
residuals = T, #残差/方差要不要体现在图中,可T和F
nCharNodes = 0
)

-
图显示mind强烈依赖于speed并且弱依赖于textual。 speed强烈依赖于X8并且弱依赖于X7。
-
线之间的值是路径系数。 路径系数是标准化的回归系数,类似于多元回归的β系数。 这些路径系数应具有统计显着性
实例2
本例说明一下SEM中的各种符号的意思
-
~:表示变量的回归关系
-
~=:用于表示测量模型,此符号的左侧为潜在变量,右侧为被测变量(即测量新的变量)
-
~~:表示方差或者协方差(也就是残余相关),当与自己用是为方差(y~~y),
加载数据
library(tidyverse)
data(airquality)
airquality <- airquality %>% na.omit()
head(airquality, 3)

本例使用测量模型,假设ET蒸散发与太阳辐射Solar.R,风速Wind和温度Temp有关,并且具有月份分异
model <- ' # 测量模型
ET =~ Solar.R + Wind + Temp + Month
Prcp =~ Wind + Temp + Month
#路径模型
ET ~ Prcp + Wind
# 残余相关
Solar.R ~~ Temp
Solar.R ~~ Month
Wind ~~ Month
Temp ~~ Month
'
fit <-sem(model, data = airquality)
summary(fit, standardized = TRUE)
结果如下
lavaan.version : '0.6.15' optim.method : 'nlminb' optim.converged : TRUE
estimator : 'ML' $estimator.args :
npar : 17 nrow.ceq.jac : 0 nrow.con.jac : 0 $con.jac.rank : 0
ngroups : 1 $nobs : 111
test : 'standard' $stat : $stat.group : refdistr : 'unknown' $pvalue :
$pe : A data.frame: 19 × 11
lhs op rhs exo est se z pvalue std.lv std.all std.nox ET =~ Solar.R 0 1.0000000 0 NA NA 1.528673e+01 0.168465989 0.168465989 ET =~ Wind 0 0.1732629 NA NA NA 2.648625e+00 0.747850227 0.747850227 ET =~ Temp 0 0.4679231 NA NA NA 7.153016e+00 0.753985247 0.753985247 ET =~ Month 0 0.0266676 NA NA NA 4.076606e-01 0.277928597 0.277928597 Prcp =~ Wind 0 1.0000000 0 NA NA 1.477120e+00 0.417070950 0.417070950 Prcp =~ Temp 0 -10.1965889 NA NA NA -1.506158e+01 -1.587611736 -1.587611736 Prcp =~ Month 0 0.2646602 NA NA NA 3.909348e-01 0.266525515 0.266525515 ET ~ Prcp 0 -6.7685765 NA NA NA -6.540310e-01 -0.654031010 -0.654031010 ET ~ Wind 0 -3.3932962 NA NA NA -2.219765e-01 -0.786163420 -0.786163420 Solar.R ~~ Temp 0 1.4467252 NA NA NA 1.446725e+00 0.000902425 0.000902425 Solar.R ~~ Month 0 -11.9111148 NA NA NA -1.191111e+01 -0.092888874 -0.092888874 Wind ~~ Month 0 0.2261809 NA NA NA 2.261809e-01 0.028092164 0.028092164 Temp ~~ Month 0 6.7520476 NA NA NA 6.752048e+00 0.262768271 0.262768271 Solar.R ~~ Solar.R 0 8000.2045245 NA NA NA 8.000205e+03 0.971619211 0.971619211 Wind ~~ Wind 0 31.5402552 NA NA NA 3.154026e+01 2.514511435 2.514511435 Temp ~~ Temp 0 -321.2542019 NA NA NA -3.212542e+02 -3.569407446 -3.569407446 Month ~~ Month 0 2.0553053 NA NA NA 2.055305e+00 0.955312219 0.955312219 ET ~~ ET 0 0.7635846 NA NA NA 3.267591e-03 0.003267591 0.003267591 Prcp ~~ Prcp 0 2.1818831 NA NA NA 1.000000e+00 1.000000000 1.000000000
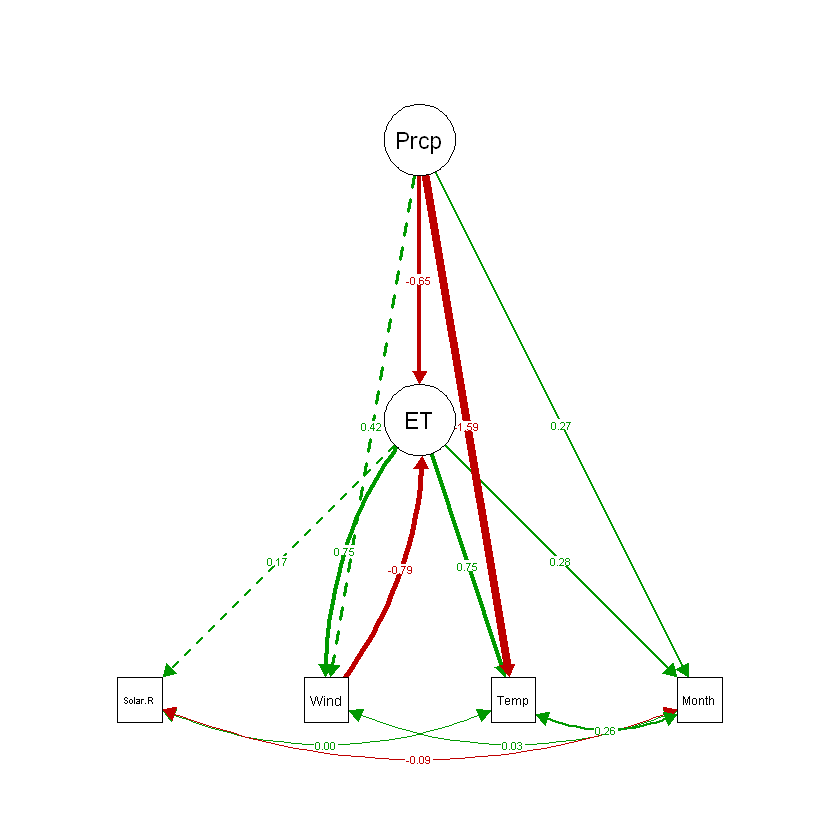
可视化结果:
semPaths(fit, #上面跑出来的数据模型
what = "std", #图中边的格式,#"path","std","est ","cons "
layout = "tree", #图的格式, tree circle spring tree2 circle2
fade = F, #褪色,按照相关度褪色
residuals = F ,#残差/方差要不要体现在图中,可T和F
nCharNodes = 0
)
本文由 mdnice 多平台发布
























 2009
2009

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










