智能算法之鸽群优化算法(PIO)，原理公式详解，附matlab代码

鸽群优化算法（pigeon-inspired optimization, PIO）是一种新型群智能优化算法，该算法是根据家鸽自主归巢行为而提出的优化算法，具有搜索速度快、进化能力强、寻优能力强等特点。该成果于2014年发表在知名SCI期刊《International journal of intelligent computing and cybernetics》上。目前在谷歌学术上有着很高的被引量，共被引577次。

鸽群优化算法是受家鸽自主归巢行为的启发而提出的优化算法，它主要借助地图和指南针算子与地标算子实现对鸽群位置和速度的更新。

算法原理

（1）地图和指南针算子

鸽子的喙结构上有磁感应结构，在飞行中使用磁性物体感知地磁场，然后在头脑中形成地图。在鸽群优化模型中，使用虚拟的鸽子模拟导航的过程，初始化鸽子的位置和速度，并且在多为搜索空间中，各自的位置和速度在每一个迭代中都会得到更新，鸽子的位置更新公式如下：  鸽子的速度更新公式如下：  式中，i=1,2,...,N为鸽子的个数

每只鸽子遵守公式： 

更新其位置Xi及速度Vi：  式中：R是地图和指南针因数，取值范围设定成0～1；rand是取值范围在0～1的随机数；Nc是目前迭代次数；Xgbest是在Nc-1次迭代循环后，通过比较所有鸽子的位置得到的全局最优位置。当循环次数达到所要求的迭代次数后，停止地图和指南针算子的工作，进入到地表算子中继续工作。

（2）地标算子

地标算子有用来模拟导航工具中地标对鸽子的影响。当鸽子飞近目的地时，鸽子更多地依赖附近的地标。在地标模型中，在每一代中用  来记录一半鸽子的个数，那些远离目的地的鸽子对地表不熟悉，它们将不再有分辨路径的能力，该阶段鸽群通过找寻周围的地标优化自身的飞行方向和速度，为了进一步减少算法的寻优时间，每次迭代都需要抛弃种群中位置较差的个体，种群数量变为上次迭代数量的一半；种群数量减半之后，计算种群中心位置，以中心位置为飞行依据，更新个体飞行方向。位置更新公式如下： 

  为鸽子更新后的位置，  为第  代所有鸽子的中心位置。F是获取适应度值的函数。根据求解方向不同可将其分为下列两种表达式，其中ε表示无穷小值。

求最小值问题求最大值问题 

 结果展示

以为CEC2005函数集为例，进行结果展示：

、

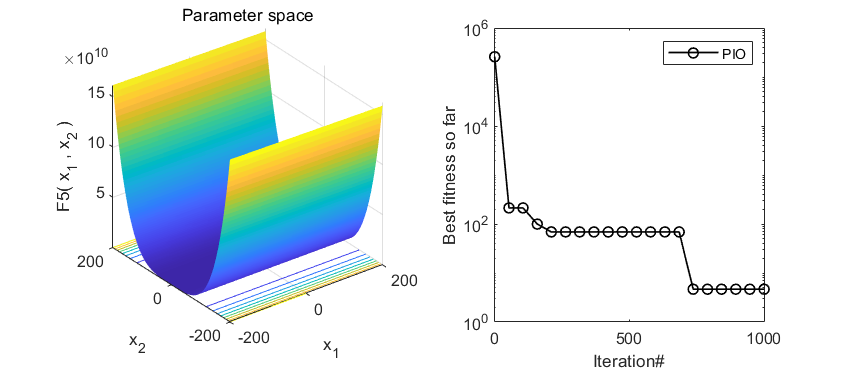
作为经典的智能优化算法，鸽群算法的效果整体来看还是不错的！

 MATLAB核心代码

function [Best_score, Best_pos,curve]=PIO(pop,Max_iter,lb,ub,dim,fobj)
Nc1= round(Max_iter*0.7);%地图因子
Nc2= Max_iter - Nc1;  %指南因子
if(max(size(ub)) == 1)
   ub = ub.*ones(1,dim);
   lb = lb.*ones(1,dim);  
end




%种群初始化
X0=initialization(pop,dim,ub,lb);
X = X0;
%计算初始适应度值
fitness = zeros(1,pop);
for i = 1:pop
   fitness(i) =  fobj(X(i,:));
end
 [fitness, index]= sort(fitness);%排序
GBestF = fitness(1);%全局最优适应度值
for i = 1:pop
    X(i,:) = X0(index(i),:);
end
curve=zeros(1,Max_iter);
GBestX = X(1,:);%全局最优位置
X_new = X;
%初始速度
Vec = rand(pop,dim);
VecNew = Vec;
%地图更新
for t = 1: Nc1
    Vec = VecNew;
    for i = 1:pop
        R = rand;
       %速度更新
       TempV=  Vec(i,:) + rand.*(GBestX - X(i,:));
       %位置更新
       TempPosition = X(i,:).*(1-exp(-R*t)) + TempV;
       %边界检查
        for j = 1:dim
           if(TempPosition(j)<lb(j) || TempPosition(j)>ub(j)) 
               TempPosition(j) = lb(j) + rand.*(ub(j) - lb(j));
               TempV(j) = rand;
           end
        end
       X_new(i,:) = TempPosition;   
       VecNew(i,:)=TempV;
    end      
   for j=1:pop
    fitness_new(j) = fobj(X_new(j,:));
   end
   X = X_new;
   fitness = fitness_new;
    %排序更新
   [fitness, index]= sort(fitness);%排序
   for j = 1:pop
      X(j,:) = X(index(j),:);
   end
   if(fitness(1) < GBestF)
       GBestF = fitness(1);
        GBestX = X(1,:);   
    end
   curve(t) = GBestF;
   
end
%指南更新
for t = 1:Nc2


   % 根据地标舍去后50%，并计算中心
   S = 0;
   for j = 1:round(pop/2)
      S = S + X(j,:).*fitness(j);      
   end


   Xcenter = S./((pop/2)*sum(fitness(1:round(pop/2))));
   %根据中心更新种群
   for i = 1:round(pop/2)
       for j = 1:dim
            Temp = X(i,j) + rand.*(Xcenter(j) - X(i,j));
            while Temp<lb(j) || Temp>ub(j)
                Temp = X(i,j) + rand.*(Xcenter(j) - X(i,j));
            end
       end
       X(i,:) = Temp;     
   end         
   for j=1:pop
    fitness(j) = fobj(X(j,:));
   end
    %排序更新
   [fitness, index]= sort(fitness);%排序
   for j = 1:pop
      X(j,:) = X(index(j),:);
   end
   
    if(fitness(1) < GBestF)
       GBestF = fitness(1);
        GBestX = X(1,:);   
    end
   curve(Nc1 + t) = GBestF;
end
Best_pos =GBestX;
Best_score = curve(end);
end

参考文献

[1] Duan H, Qiao P. Pigeon-inspired optimization: a new swarm intelligence optimizer for air robot path planning[J]. International journal of intelligent computing and cybernetics, 2014, 7(1): 24-37.

完整代码获取方式：后台回复关键字：

TGDM990