2024最新：鳑鮍鱼优化算法(BFO)，原理公式详解，附matlab代码

最新推荐文章于 2024-08-27 10:03:45 发布

淘个代码_

最新推荐文章于 2024-08-27 10:03:45 发布

阅读量2.2k

点赞数 24

文章标签：算法 matlab 开发语言

本文链接：https://blog.csdn.net/woaipythonmeme/article/details/136550134

版权

鳑鮍鱼优化算法（Bitterling fish optimization algorithm，BFO）是一种受自然启发的群智能优化算法，鳑鮍鱼是自然界中为了生存而做出聪明行为的典型例子。该算法基于这些鱼的交配行为对鳑鮍鱼优化算法进行建模。在各种基准函数上的实验和实现表明，鳑鮍鱼优化算法比灰狼优化算法、鲸鱼优化算法、蝴蝶优化算法和哈里斯鹰优化算法算法更精确。该成果于2024年发表在知名SCI期刊Multimedia Tools and Applications上。

BFO算法灵感来自于鳑鮍鱼独特的繁殖机制。

在动物界，鱼的繁殖发生得尽可能早。在交配时，雄性和雌性相互靠近，然后将精子和卵子释放到水中，但这种方法有一个很大的缺点。幼鱼暴露在各种外部危险中，很容易成为其他动物的猎物。

鳑鮍鱼有不同的繁殖机制。这种鱼以牡蛎为食。寻找适合产卵的壳是雄性的责任。它们需要找到更大的牡蛎，有更多的空间来容纳它们的卵。当这些鱼找到一个或多个牡蛎时，它们会反抗它们的敌人。雄性物种攻击性行为的原因是其他一些雄性物种也倾向于把牡蛎占为己有。在战斗模式下，雄鱼的身体颜色变暗，并尽其所能捍卫自己的领土。在交配阶段，发生了一种叫做性选择的现象。在性选择过程中，雌鱼根据颜色和体力选择雄鱼。从图可以看出，雌鱼通常会带来体型更大、身体颜色更漂亮的雄鱼。这时，雌鱼在牡蛎里产卵，然后雄鱼用精子使它们受精。

1、算法原理

（1）种群初始化

该问题的每个解决方案都是一条鳑鮍鱼或一个鱼卵，如下式所定义:

我们可以考虑几个作为随机种群产生的鳑鮍鱼种群，如下式所示:

D的值是每个解的维度或决策变量的数量。i的值也是问题的解决方案。F的值是n的素种群的矩阵。Fj i表示第i个解的维度j。在区间[l，u]中创建的群体。下式创建了初始种群：

r是0和1之间的随机数。

（2）评估解决方案

在BFO算法中，问题的每个解都是一条鱼。为了评价每个方案，我们可以关注其牡蛎的选择。每条鱼都有自己的优点，这取决于它选择了合适的牡蛎，并吸引了其他雌鱼。目标函数(如f)用于评估每个鱼或解决方案。在下式中，每个解决方案的能力在能力矩阵中定义：

（3）搜查及检取牡蛎

任何解决方案或鱼都可以搜索问题空间并找到合适的交配牡蛎。在提出的方法中，每条鱼都有资格被定位在具有更优壳的区域。鱼可以漫游寻找牡蛎，在这种情况下，它以牡蛎为目标并向它移动。在这种情况下，目标牡蛎没有被另一条鱼注意到，被这条鱼捕获。牡蛎占有状态用下式表示:

在这个方程中，Fti和Ft+1 i分别是鱼在t和t+1迭代中的当前位置和新位置，对于鱼或第i个解。

F*也是最优解或最优解。F+是随机选择的种群中牡蛎的价值之一。δ和r是0到1之间的随机数。

J是鱼为了逃离或接近牡蛎而移动的步数或速度，这个因素通过迭代算法来减少。参数J下降的原因是一段时间后，雄鱼的活动减少了，因为它们成功交配了。随着时间的推移，减小J会导致全局搜索减少到局部搜索。为了减小参数J，使用以下公式:

J(1)是每条鱼在初始迭代中的步长和跳跃值。t和MaxIt的值分别是当前和最大迭代次数。J (t)是每条鱼在重复t中寻找牡蛎的步数和跳数。随机函数U使用下式生成随机序列:

U（1）可以被认为等于1，新公式方程如下：

在BFO算法中，最优解是随着时间的推移和在最优解周围更多的空间重复来搜索的。因此，有必要将参数P随时间减小到公式(5)的第二个准则，条件为r > P，这是最有可能做到的。参数p采用类似于arctan行为的函数，如下式:

t的值是重复计数器，a等于还原的幂。

（4）逃离牡蛎，不要抓住牡蛎

在逃避和不抓住牡蛎的行为中，另一条鱼照顾牡蛎，使鱼避免接近牡蛎，并选择另一个位置。方程（10）用于逃避或意外寻找一条没有成功捕获牡蛎的鱼：

M的值等于鱼群的平均位置。对此，鳑鮍鱼既然逃走了，就可以搜索平均与最优之间的空间问题，或者搜索随机空间问题。用下式计算人口重力点:

（5）生产

雄鱼通过选择自己想要繁殖的牡蛎来吸引雌鱼，以此来炫耀自己的健康。在这个阶段，雌性物种将其卵状管状器官插入牡蛎中，将它们运送到宿主的身体空间，这在鱼类和水生动物中是非常奇怪的。在这个过程之后，雄性进入手术并将其精子转移到牡蛎体内受精。当卵和幼虫孵化时，它们的脆弱性略有降低。牡蛎将水中漂浮的食物颗粒输送到体内。在这个阶段，幼鱼比牡蛎先吃水溶性固体。苦味鱼的幼虫也会从宿主那里窃取氧气，因此有寄生行为。这些小鱼在这个空间里待的时间足够长，以牡蛎为食，为进入外面的世界做准备。

雄鱼发现牡蛎后，可以吸引雌鱼在牡蛎中产卵，雄鱼可以使卵受精，在现有的鱼周围产生新的鱼，如下式:

R是鱼在壳周围的分布半径。该半径的初始值在[0,2]范围内。通常，该参数的值最初被认为等于2，并根据BFO算法的迭代随着时间的推移而减小。

（6）捕鱼

一只牡蛎可以容纳好几条小鱼；一些较弱的会被牡蛎或捕食者猎杀。失去一个解决方案的概率可以被认为与它的优点成反比。假设问题为最小化类型，损失一条鱼的概率如下式所示:

消除解Ft i的概率等于d(Ft i) f(Ft i)是这个解的目标函数值。

2、结果展示

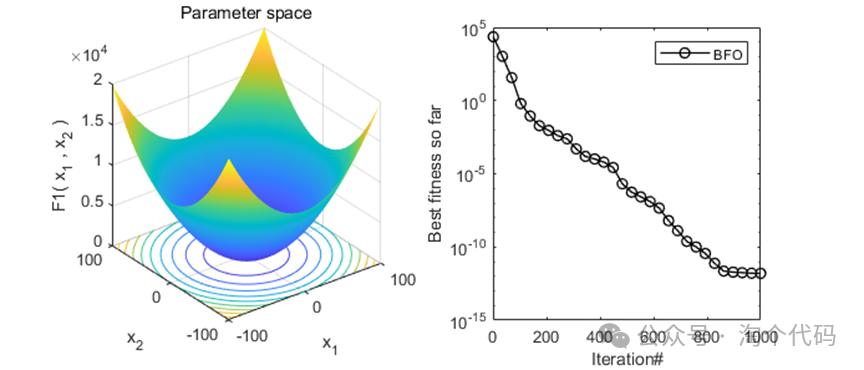
3、MATLAB核心代码

%% 淘个代码 %%
% 微信公众号搜索：淘个代码，获取更多代码
% 鳑鮍优化算法（BFO）
function  [BestSol,BestCosts] =BFO(nPop,MaxIt,VarMin,VarMax,nVar,CostFunction)
Wmax=2;
Wmin=0;
%% BFO Parameters
VarSize=[1 nVar];
solution=[];
solution.Position=[];
solution.Cost=[];
pop=repmat(solution,nPop,1);
BestSol.Cost=inf;
for i=1:nPop
    pop(i).Position=unifrnd(VarMin,VarMax,VarSize);
    pop(i).Cost=CostFunction(pop(i).Position);
    if pop(i).Cost < BestSol.Cost
        BestSol=pop(i);
    end
end
BestCosts=zeros(MaxIt,1);
[~, SortOrder]=sort([pop.Cost]);
poptemp = pop(SortOrder);
N=ceil(nPop/3);
pop_plus=poptemp(1:N);
%% BFO main
SD0=1;
p=1;
Hmax=5;
U=0.7;
J=1;
for it=1:MaxIt
    %%
    P= abs(1-it/(sqrt(1+it*it)))+rand/(it^0.5);
    U=(1-it/MaxIt)*cos(it*acos(U));
    J=(J-(J/it)/MaxIt)*U;
    R=2*rand;
    SD = SD0-(p/pi)*(atan(it*p/pi));
    Costs = [pop.Cost];
    WorstCost = max(Costs);
    alpha=1-(it/MaxIt)^2;
    beta=1-alpha;
    newpop = [];
    %%---- Search oysters
    for i=1:nPop
        newsol=solution;
        A=1:N;
        %          A(i)=[];
        j=A(randi(N-1));
        if rand<P
newsol.Position=pop(i).Position+(rand(VarSize).*(pop_plus(j).Position-J*pop(i).Position));
        else
newsol.Position=pop(i).Position+(rand(VarSize).*(BestSol.Position-J*pop(i).Position));
        end
        newsol.Position=max(newsol.Position,VarMin);
        newsol.Position=min(newsol.Position,VarMax);
        newsol.Cost=CostFunction(newsol.Position);
        if newsol.Cost < pop(i).Cost
            pop(i)=newsol;
            if pop(i).Cost < BestSol.Cost
                BestSol=pop(i);
            end
        end
    end
    %% Means
    MMM=0;
    for i=1:nPop
        MMM=MMM+pop(i).Position;
    end
    MMM=MMM/nPop;
    for i=1:nPop
        if pop(i).Cost < BestSol.Cost
            BestSol=pop(i);
        end
    end
    %%--- Escape
    for i=1:nPop
        newsol=solution;
        if rand<P
            newsol.Position=pop(i).Position+(rand(VarSize).*(BestSol.Position-J*MMM));
            %                 newsol.Position=J*pop(i).Position+(rand(VarSize).*(BestSol.Position-J*MMM));% for complix
        else
            newsol.Position=unifrnd(VarMin,VarMax,VarSize);
        end
        newsol.Position=max(newsol.Position,VarMin);
        newsol.Position=min(newsol.Position,VarMax);
        newsol.Cost=CostFunction(newsol.Position);
        if newsol.Cost < pop(i).Cost
            pop(i)=newsol;
            if pop(i).Cost < BestSol.Cost
                BestSol=pop(i);
            end
        end
    end
    %%---
    for i = 1:numel(pop)
        H=(exp(-1*pop(i).Cost/WorstCost))*Hmax;
        for j = 1:H
            newsol = solution;
            if rand<=0.5
                newsol.Position = pop(i).Position +R* SD * randn(VarSize);
            else
                newsol.Position = pop(i).Position -R* SD * randn(VarSize);
            end
            newsol.Position = max(newsol.Position, VarMin);
            newsol.Position = min(newsol.Position, VarMax);
            newsol.Cost = CostFunction(newsol.Position);
            newpop = [newpop
                newsol];  %#ok
        end
    end
    pop = [pop
        newpop];
    [~, SortOrder]=sort([pop.Cost]);
    pop = pop(SortOrder);
    if numel(pop)>nPop
        pop = pop(1:nPop);
    end
    %%
    for i=1:nPop
        newsol=solution;
        W=Wmax-(((Wmax-Wmin)*it)/MaxIt);
        newsol.Position=pop(i).Position+beta*(rand(VarSize).*(BestSol.Position-rand*MMM));
        %         newsol.Position=alpha*pop(i).Position+beta*(rand(VarSize).*(BestSol.Position-rand*MMM));% for complix fun
        newsol.Position=max(newsol.Position,VarMin);
        newsol.Position=min(newsol.Position,VarMax);
        newsol.Cost=CostFunction(newsol.Position);
        if newsol.Cost < pop(i).Cost
            pop(i)=newsol;
            if pop(i).Cost < BestSol.Cost
                BestSol=pop(i);
            end
        end
    end
    for i=1:nPop
        A=1:nPop;
        A(i)=[];
        j=A(randi(nPop-1));
        Step=pop(i).Position-pop(j).Position;
        if pop(j).Cost < pop(i).Cost
            Step=-Step;
        end
        newsol=solution;
        newsol.Position=pop(i).Position+rand(VarSize).*Step;
        newsol.Position=max(newsol.Position,VarMin);
        newsol.Position=min(newsol.Position,VarMax);
        newsol.Cost=CostFunction(newsol.Position);
        if newsol.Cost < pop(i).Cost
            pop(i)=newsol;
            if pop(i).Cost < BestSol.Cost
                BestSol=pop(i);
            end
        end
    end
    % Matting
    for i=1:nPop
        A=1:nPop;
        A(i)=[];
        j1=A(randi(nPop-1));
        A(A==j1)=[];
        j2=A(randi(nPop-2));
        A(A==j2)=[];
        j3=A(randi(nPop-3));
        newsol=solution;
        newsol.Position=pop(j1).Position+rand(VarSize).*(pop(j2).Position-pop(j3).Position);
        newsol.Position=max(newsol.Position,VarMin);
        newsol.Position=min(newsol.Position,VarMax);
        newsol.Cost=CostFunction(newsol.Position);
        if newsol.Cost < pop(i).Cost
            pop(i)=newsol;
            if pop(i).Cost < BestSol.Cost
                BestSol=pop(i);
            end
        end
    end
    BestCosts(it)=BestSol.Cost;
    [~, SortOrder]=sort([pop.Cost]);
    poptemp = pop(SortOrder);
    N=ceil(nPop/4);
    pop_plus=poptemp(1:N);
end
End

参考文献

[1] Zareian L, Rahebi J, Shayegan M J. Bitterling fish optimization (BFO) algorithm[J]. Multimedia Tools and Applications, 2024: 1-34.

完整代码获取方式：后台回复关键字：

TGDM866