2023年JCR1区新算法：二次插值优化算法（QIQ），MATLAB代码免费获取

最新推荐文章于 2024-09-01 08:52:35 发布

淘个代码_

最新推荐文章于 2024-09-01 08:52:35 发布

阅读量1.6k

点赞数 20

文章标签：算法 matlab 开发语言

本文链接：https://blog.csdn.net/woaipythonmeme/article/details/136668478

版权

文章介绍了QIO算法，一种结合广义二次插值的新型优化方法，通过改进的搜索策略有效求解优化问题，具有高效搜索和寻优特性。算法通过自适应参数平衡探索与开发，以找到全局最优解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二次插值优化算法（Quadratic Interpolation Optimization，QIO）是一种全新的元启发式优化方法，其灵感源自数学领域，特别是近期提出的广义二次插值（Generalized Quadratic Interpolation，GQI）方法。相较于传统的二次插值方法，QIO克服了其局限性，更有效地求解由任意三个点构成的二次函数的极小值。QIO将广义二次插值方法作为一种前瞻性的搜索机制，用于解决各种类型的优化问题，具有进化能力强、搜索速度快、寻优能力强的特点。该成果于2023年发表在计算机领域一区期刊Computer Methods in Applied Mechanics and Engineering上。

作者设计了一种基于数学的QIO优化方法。在QIO算法中，提出了能够求出任意二次函数最小值的GQI方法，并给出了两种强大的搜索策略。在探索策略中，对于每一个维度，使用GQI方法求得由种群中随机选择的两个个体与当前个体的位置构成的二次插值函数的最小值，将得到的最小值与从总体中随机选择的另一个个体的位置相结合，产生执行全局搜索的新位置。

1、算法原理

（1）二次插值法

二次插值法是一种常用的曲线拟合技术，常用于一元函数在给定的初始区间内寻找最小点。在求函数f(x)的极小点的过程中，使用二次插值多项式L(x)来逼近函数f(x)。通过求多项式L(x)的极小值，可以得到函数f(x)的近似极小点。二次插值的基本公式如下:

f(x)的二次插值函数L(x)可表示为:

（1）

其中α，β，δ为待定系数。

二次插值被广泛用于逼近f(x)的最小值。在优化领域，它经常被集成到各种各样的优化技术中，以提高其搜索性能。但在实际应用中，处理极小化问题时，对三点的选取没有具体要求。然而，当点选择不当时，可能会构造一个向上开口的抛物线，导致最大化而不是最小化。如果对选择三个点来建立向下开口的抛物线有具体要求，这种限制在时间消耗和有效性方面带来了挑战。为了解决这个问题，并满足更普遍的方法的需求，广义二次插值（GQI）方法被提出。

（2）勘探战略

探索是指算法彻底搜索整个变量空间以识别可能包含全局最优解的有希望区域的能力，从而避免局部最优或过早收敛。通过搜索不同的区域，探索有助于避免忽略任何潜在的区域，并发现不同的和改进的解决方案。GQI方法被用来确定所提出的QIO的勘探策略。该方法将当前种群中随机选取的两个个体与当前个体共同用于GQI方法，得到了由三个位置组成的插值函数的极小值点，从而确定了有希望的区域.同时，从当前种群中随机选择第三个个体来产生新的候选解。它可以增强种群多样性。当使用GQI方法执行探查时，当前个体的位置更新为：

（2）

（3）

其中，xrand1，xrand2，xrand3是当前总体中随机选择的不同个体的位置，r1，r2，r3为(0,1)中的随机数，并且fit(·)表示函数适应度值，GQI(xi(t))，Xrand1(t)，Xrand2(t)，fit(xi(t))，fit(Xrand1(t))，fit(Xrand2(t))是GQI函数，通过它可以得到由(xi,fit(xi))，(xrand2,fit(xrand2)) 和(xrand3,fit(xrand3))组成的插值函数的最小化。

GQI方法能有效地扩大搜索范围，有助于定位有希望的区域。为了使算法能够首先进行探索，然后平衡探索和开发，并最终收敛到最优解，一个重要的参数被称为探索权重的引入，它可以通过使用自适应系数b来改变。它们分别表示为：

（4）

（5）

（6）

其中，t1遵循标准正态分布，t是迭代次数，T是最大迭代次数。下图表示出了自适应参数B相对于迭代次数的变化。下图中的曲线揭示了参数B在整个迭代中的总体趋势。在迭代的早期阶段，参数B取较大的值，这有助于算法探索搜索空间的有希望的区域并促进种群多样性。随着迭代的进行，B的值逐渐增加，确保从探索阶段到开发阶段的平滑过渡。值得注意的是，沿着曲线有两个变化沿着。首先，在迭代次数为120 ~ 240时，b值先增大后减小，使算法避免陷入局部最优;其次，在迭代次数为300 ~ 450时，b值下降较慢，有助于防止早熟收敛，提高算法的搜索能力。

（3）开发战略

Exploitation通常与Exploration形成对比，因为它专注于通过本地搜索提炼迄今为止找到的最佳解决方案。Exploitation的目标是更快地收敛，更接近全局最优解。在QIO中，在开发阶段，从当前种群中随机选择两个个体，并在GQI方法中使用迄今为止找到的最佳个体来产生更好的解决方案。该算法能够在极小点周围的区域内找到全局最优解。因此，当QIO执行利用时，当前个体的位置更新为：

（7）

（8）

（9）

其中n2服从标准正态分布，rD是来自[1,d]的随机整数，LbrD和UbrD是第rD维的下边界和高边界。w2为开发权值，是一种自适应系数。下图描述了自适应参数w2相对于迭代的变化。可以看出，w2的值随着迭代次数的增加逐渐减小，这有助于显著提高收敛精度。

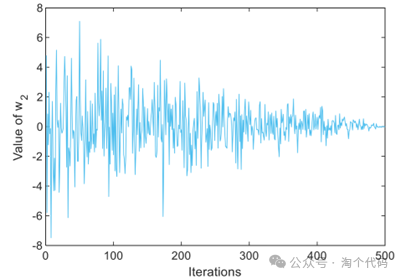
从Eq.(8)中可以看出，目前为止找到的最优个体xbest和随机选择的两个个体xrand1和xrand2被用在GQI方法中，以产生最小值xbest,rand1,rand2，总体上优于三个个体。第i个个体的更新是通过用随机扰动来搜索xbest,rand1,rand2相对于xbest的邻域。这种搜索可以帮助算法进行有效的开发而不停滞。在完成勘探和开采策略后，根据以下公式更新ith个体的位置:

（10）

如果第i个个体的候选位置的适应度值优于当前位置，则将i个个体的位置替换为其候选位置。否则，保持不变。

QIO算法通过生成一组随机解来启动。在每次迭代中，当rand > 0.5时，算法使用Eq.(3)获得当前个体和随机选择的两个个体的GQI函数的最小值，并使用Eq.(2)进行探索。当rand≤0.5时，算法使用Eq.(8)获得GQI函数的最小值，其中包含迄今为止找到的最佳个体和随机选择的两个个体，并使用Eq.(7)进行开发。当勘探或开发完成时，使用公式(10)更新到目前为止找到的最佳解决方案。最终，当满足预先建立的终止条件时，QIO算法停止，并返回到目前为止找到的最佳解决方案，QIO的流程图如图12所示。

2、结果展示

3、MATLAB核心代码

%% 淘个代码 %%
% 微信公众号搜索：淘个代码，获取更多代码
% 二次插值优化算法（QIO）
function [BestX,BestF,HisBestF]=QIO(FunIndex,MaxIt,nPop)
[Low,Up,Dim]=FunRange(FunIndex);
IndividualsPos=zeros(nPop,Dim);
IndividualsFit=zeros(nPop,1);
if length(Low)==1
    Low=ones(1,Dim)*Low;
    Up=ones(1,Dim)*Up;
end
for i=1:nPop
    IndividualsPos(i,:)=rand(1,Dim).*(Up-Low)+Low;
    IndividualsFit(i)=BenFunctions(IndividualsPos(i,:),FunIndex,Dim);
end
BestF=inf;
BestX=[];
for i=1:nPop
    if IndividualsFit(i)<=BestF
        BestF=IndividualsFit(i);
        BestX=IndividualsPos(i,:);
    end
end
HisBestF=zeros(MaxIt,1);
for It=1:MaxIt
    newIndividualPos=zeros(1,Dim);
    for i=1:nPop
        if rand>0.5
            K=[1:i-1 i+1:nPop];
            RandInd=randperm(nPop-1,3);            
            K1=K(RandInd(1));
            K2=K(RandInd(2));
            K3=K(RandInd(3));
            f1=IndividualsFit(i);
            f2=IndividualsFit(K1);
            f3=IndividualsFit(K2);
            for j=1:Dim
                x1=IndividualsPos(i,j);
                x2=IndividualsPos(K1,j);
                x3=IndividualsPos(K2,j);
                % Eq.(25)
                newIndividualPos(j)=GQI(x1,x2,x3,f1,f2,f3,Low(j),Up(j));
            end
            a=cos(pi/2*It/MaxIt);
            b=0.7*a+0.15*a*(cos(5*pi*It/MaxIt)+1);
            % Eq.(27)
            w1=3*b*randn;
            % Exploration, Eq.(26)
            newIndividualPos=newIndividualPos+w1.*(IndividualsPos(K3,:)-...
                newIndividualPos)+round(0.5*(0.05+rand))*(log(rand/(rand)));
        else
            K=[1:i-1 i+1:nPop];
            RandInd=randperm(nPop-1,2);
            K1=K(RandInd(1));
            K2=K(RandInd(2));
            f1=IndividualsFit(K1);
            f2=IndividualsFit(K2);
            f3=BestF;
            for j=1:Dim
                x1=IndividualsPos(K(RandInd(1)),j);
                x2=IndividualsPos(K(RandInd(2)),j);
                x3=BestX(j);
                %Eq.(31)
                newIndividualPos(j)=GQI(x1,x2,x3,f1,f2,f3,Low(j),Up(j));
            end
            %Eq.(32)
            w2=3*(1-(It-1)/MaxIt)*randn;
            rD=randi(Dim);
            %Exploitation, Eq.(30)
            newIndividualPos=newIndividualPos+w2*(BestX-round(1+rand)*...
                (Up-Low)/(Up(rD)-Low(rD))*IndividualsPos(i,rD));
        end
        newIndividualPos=SpaceBound(newIndividualPos,Up,Low);
        newIndividualFit=BenFunctions(newIndividualPos,FunIndex,Dim);
        %Eq.(33)
        if newIndividualFit<IndividualsFit(i)
            IndividualsFit(i)=newIndividualFit;
            IndividualsPos(i,:)=newIndividualPos;
        end
    end
    for i=1:nPop
        if IndividualsFit(i)<BestF
            BestF=IndividualsFit(i);
            BestX=IndividualsPos(i,:);
        end
    end
    HisBestF(It)=BestF;
end

参考文献

[1] Zhao W, Wang L, Zhang Z, et al. Quadratic Interpolation Optimization (QIO): A new optimization algorithm based on generalized quadratic interpolation and its applications to real-world engineering problems[J]. Computer Methods in Applied Mechanics and Engineering, 2023, 417: 116446.

完整代码获取方式：后台回复关键字：

TGDM866