注:该算法已按照智能优化算法APP标准格式进行整改,可直接集成到APP中,方便大家与自己的算法进行对比。目前优化算法APP已经更新到了6.0版本,功能越来越丰富啦!
投影迭代优化器(Projection-Iterative-Methods-based Optimizer, PIMO)是一种全新构建的元启发式算法,灵感源自经典数值分析中的投影迭代法。该方法广泛用于求解大型线性方程组,以其收敛性稳定、结构简洁著称。PIMO 则首次将这一“数学求解思想”引入智能优化框架中,模拟出一套具备方向引导性与快速调整性的搜索机制。PIMO 巧妙地融合了Kaczmarz 方法的行空间投影思想与随机梯度下降(SGD)的鲁棒自适应特性,提出四种核心算子:初始化扰动、精细投影、随机修正与全局引导,从而在保持搜索广度的同时,实现对局部最优的有效规避。这一设计不仅增强了算法的收敛速度与稳定性,更使其在处理复杂、多约束优化问题中表现出卓越的泛化能力。

该成果于2025年6月发表于中科院一区期刊Knowledge-Based Systems(中科院一区,影响因子7.6),为数学机制驱动的智能优化提供了一种全新范式。
1、算法原理
(1)算法启发
投影方法在约束优化中被广泛应用,主要用于在每次更新中确保解满足约束条件。通过该操作,可以避免优化过程中解违反约束条件,从而防止产生不符合实际的结果。特别是在具有复杂约束的非线性优化问题中,投影方法展现出其独特的优势。在此背景下,本文受到投影方法的启发,设计了一种基于投影-迭代方法的优化器(Projection-Iterative-Methods-based Optimizer, 简称 PIMO)。设目标函数为 ,其中 是解向量,约束集合为 。约束集合 定义了所有可行解的位置,该优化问题可表示为:
х
在每次迭代中,我们获得的解可能会违反约束条件。为了确保每个解始终处于可行域内,我们通过投影操作将当前解映射回约束集合 。在投影迭代方法中,通过持续地对当前解进行投影操作,确保解在每次更新后位于可行域内。假设当前解为 ,即第 次迭代中第 个解。对该解 进行投影,并将其映射回约束集合 ,投影算子为:
设第 次迭代中第 个解的函数值为 ,当前的最优解为 ,对应的最优位置通过投影操作获得。
投影的核心思想是:当当前解违反约束条件时,通过投影操作将其映射至约束区域,从而使其成为一个可行解。该过程不仅有助于保持解的可行性,还能使算法在优化过程中避免大量的约束违反,从而提高优化效率。
(2)投影簇初始化
PIMO 首先初始化种群以启动优化过程,设定种群数量为 ,变量维度为 。每一个经过投影的个体作为一个搜索代理参与算法搜索,所有个体构成算法的完整搜索群体。每个个体可由如下数学表达式表示:
其中, 表示第个投影搜索个体的第维, 表示在区间内的随机数; 和 分别为变量的下界和上界,其数学表达式定义如下:
(3)残差引导投影
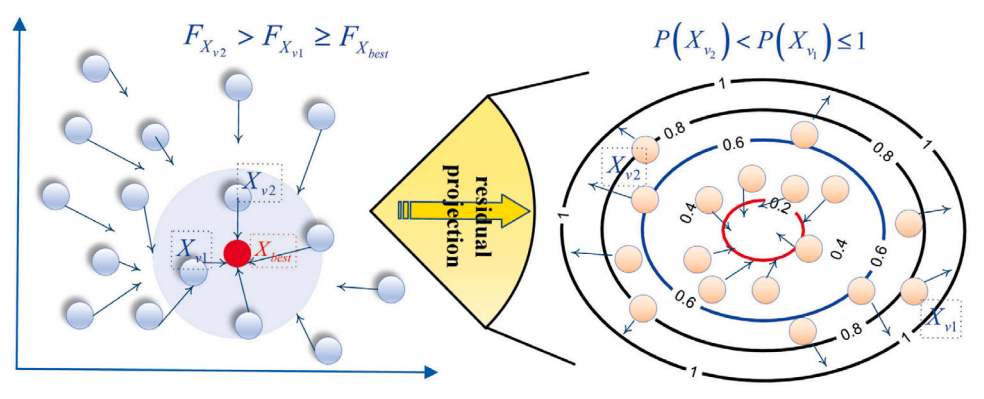
在残差引导投影(Residual Guided Projection, RGP)过程中,算法通过在多维空间中不断投影来逼近最优解。将 Kaczmarz 行动逐行迭代更新策略与随机梯度下降(SGD)相结合,建立了一个协同混合框架,为高维解空间中的轨迹提供系统性指导。基于残差思想,在每次迭代选择投影方程时加入了随机梯度的理念。具体来说,通过比较随机数 和 ,RGP 决定采用“随机”或“最优”选择策略。该决策过程具有概率性质,从而增强了算法的探索性。在 RGP 中,随机选取两个残差适应度较小的最优解粒子或样本( 和 )作为引导代理,并基于该代理计算梯度以指导投影方向。这样,解的更新不仅依赖于当前解的投影,还基于梯度加速收敛并避免陷入局部最优。其数学表达式如下:
当 时,残差 通常表示当前解与目标解之间的差异,而平方残差 则更突出较大的误差,有助于 RGP 过程更加聚焦于较差的解。值得注意的是,该过程对每个解的平方残差 进行归一化处理,归一化因子为所有解的平方残差之和,从而得到概率分布 。残差越接近 1,解被选中的概率越高,使得更新过程更加集中于当前解误差较大的区域。通过这种方式,RGP 过程能够主动“修正”误差较大的解,提高全局优化的效率。
当 时,RGP 选择当前的 。这种选择策略有助于局部的精细搜索。通过直接使用 (当前最优解)作为投影目标,算法将当前解收敛到全局最优解。该方法保证当解已经接近最优时,算法能够更高效地进行微调以实现最终收敛。RGP 过程的具体选择如下图所示。
在更新解的过程中,RGP 不仅利用所选代理与最优解之间的梯度信息 ,还通过雅可比矩阵对解进行进一步调整,如以下公式所示:
其中, 、 、 为取值在 0 到 1 之间的随机数。雅可比矩阵 是描述非线性优化问题中解对输入变化敏感性的关键工具。通过对目标函数 进行雅可比计算,RGP 能基于目标函数的局部线性化,执行更为精确的投影更新。
目标函数 输出一个维向量,输入为一个维向量。雅可比矩阵的元素表示目标函数第个分量对变量 的偏导数:
是目标函数的第个分量。 是标准基向量,在第个位置为 1,其余位置为 0, 是一个很小的扰动值。对于每个维度,通过扰动 来计算目标函数的差分,从而获得每个分量的雅可比值:
最终,雅可比矩阵 包含所有 元素,矩阵尺寸为 :
通过对目标函数进行雅可比计算,RGP 能基于目标函数的局部线性化执行更为精确的投影更新。因此,位置更新是投影操作与梯度信息的结合。
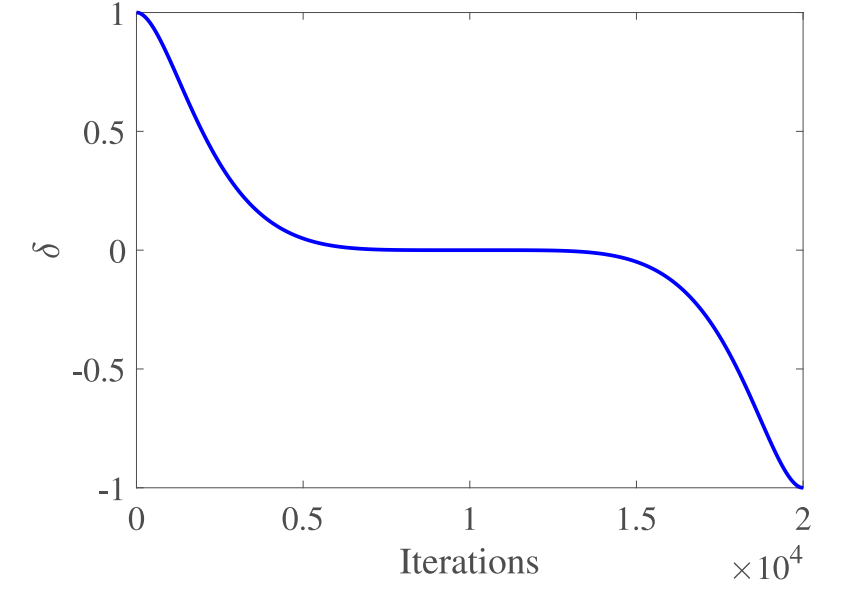
其中, 是当前搜索个体。 用于调整基于梯度的投影更新方向。 是随迭代变化的动态参数,其表达式如公式所示:
用于表示动态衰减步长,即随着迭代的进行,更新幅度逐渐减小,从而避免优化后期出现过度调整,具体见下图所示。RGP 动态选择结合梯度与投影的方法更新解。当满足某种情况时,RGP 采用基于梯度的投影更新方法;否则,RGP 利用雅可比矩阵方法指导投影更新。该策略提升了算法的灵活性与适应性。
(4)双重随机投影
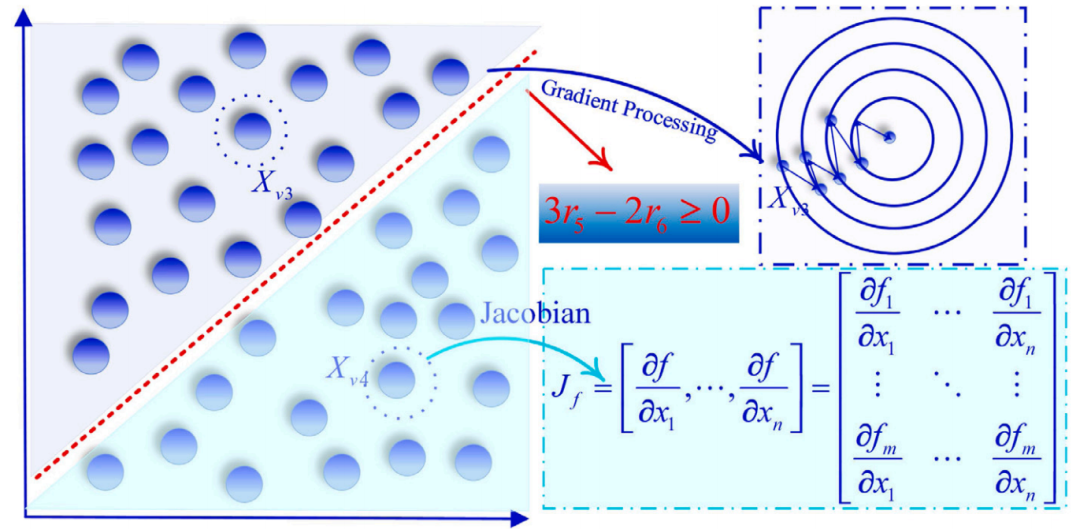
双重随机投影过程通过引入双重随机性增强了算法的全局搜索能力。算法首先从粒子群中随机选择两个索引 和 ,作为投影更新的参考点。该过程通过均匀随机化实现,以确保选择过程的多样性。具体如以下公式:
当随机决定采用梯度更新时,算法基于粒子当前的位置 、 与当前最优位置之间的差异计算更新方向,如公式所示:
梯度投影更新利用两个点的加权平均差值,即 和 ,基于这两点对当前解的影响权衡,调整当前搜索位置的方向。当过程决定采用雅可比矩阵投影更新时,DRP 首先在当前位置计算雅可比矩阵 ,为后续更新提供更精确的方向指导。更新方向的表达式如下:
雅可比矩阵 提供多变量目标函数的偏导信息,使更新更加准确,尤其在高维空间中。更新公式将方向信息与雅可比矩阵的投影映射相结合,既实现快速调整,又能跳出复杂函数的非凸区域。具体的双重随机投影(DRP)过程见下图所示。
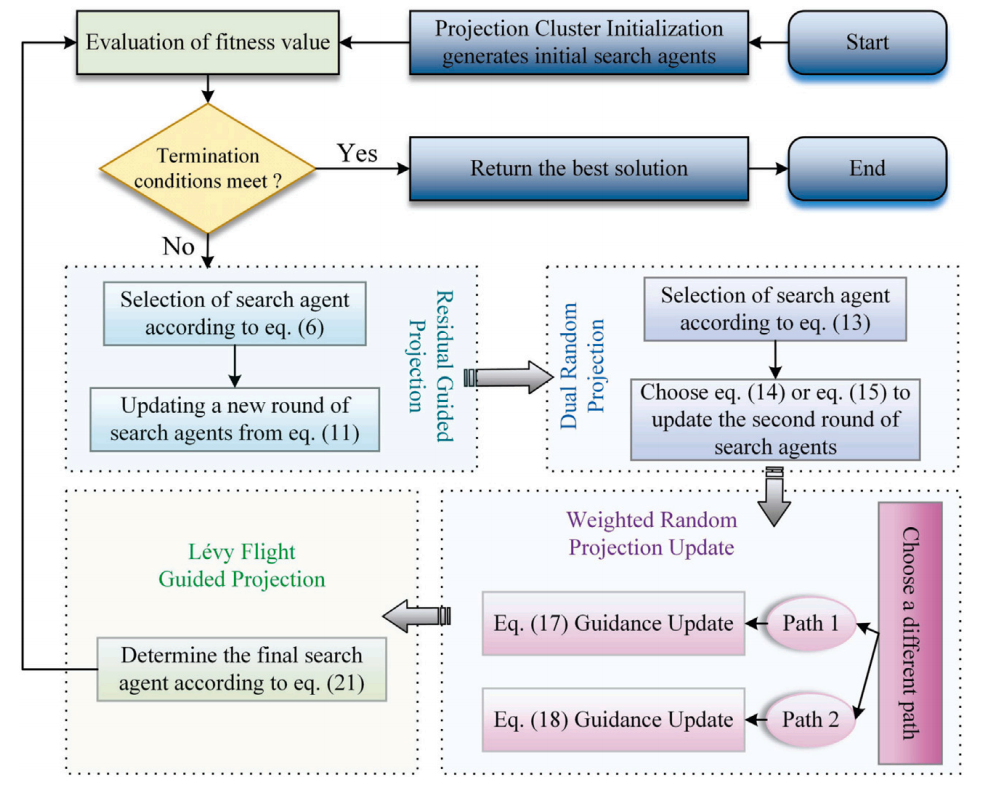
所提出的PIMO算法的完整流程如下图所示:
PIMO算法的伪代码如下:

2、结果展示
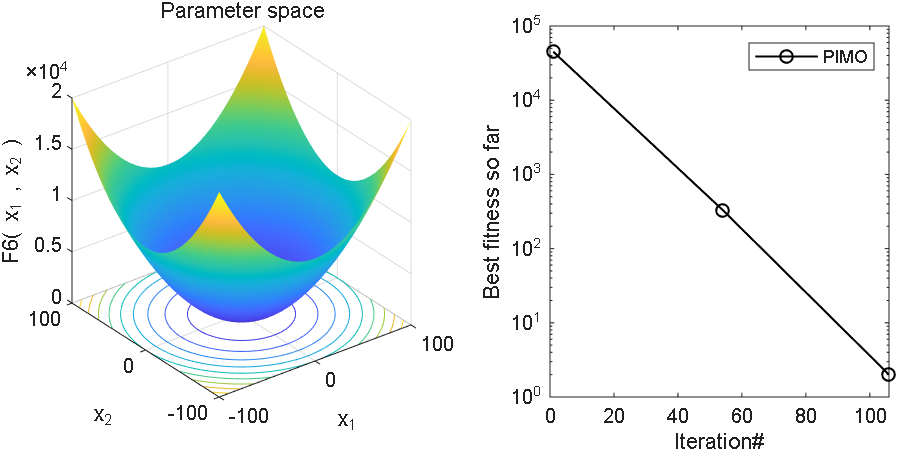
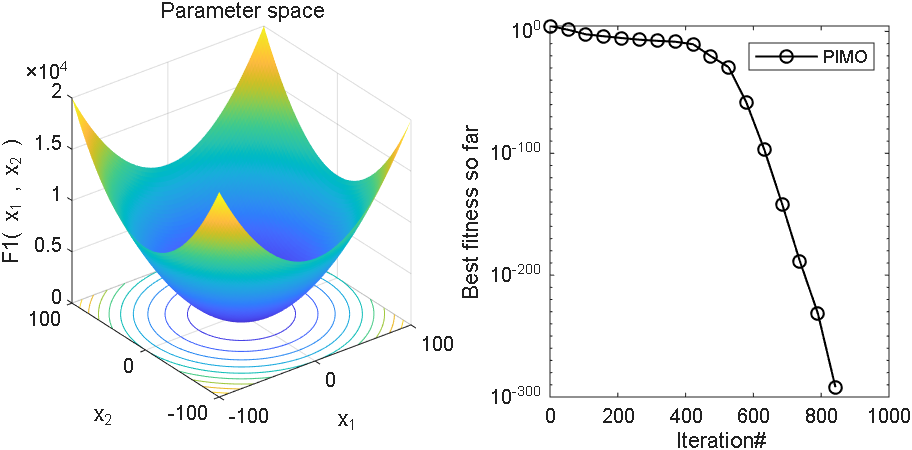
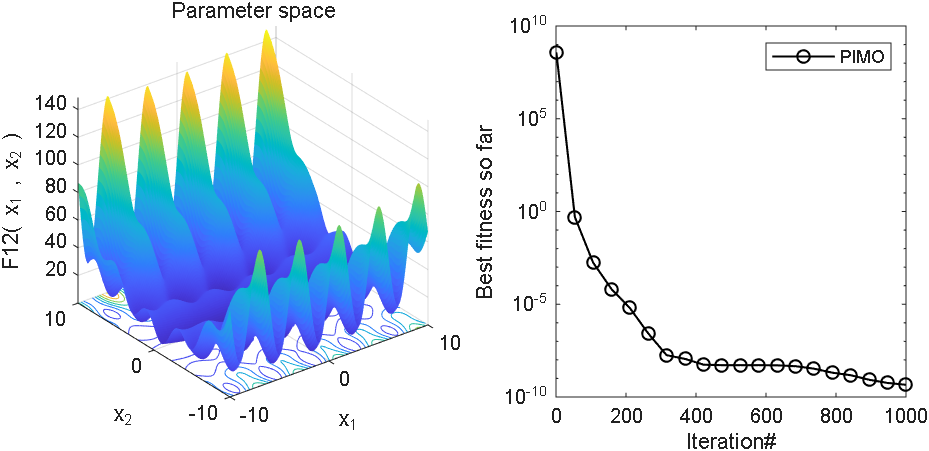
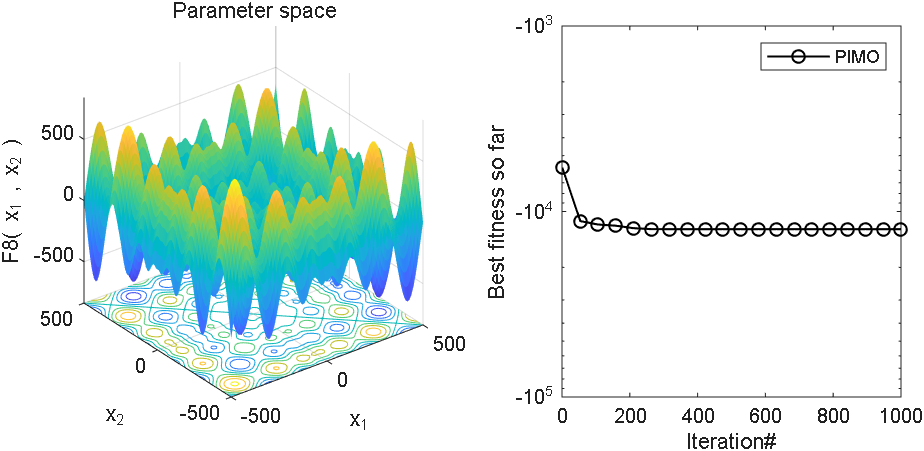
3、MATLAB核心代码
3、MATLAB核心代码
%% 淘个代码 %%
% 微信公众号搜索:淘个代码,获取更多代码
% 投影迭代优化器(Projection-Iterative-Methods-based Optimizer, PIMO)
function [Best_Score, Best_Pos, CG_curve] = PIMO(N, Max_iter, lb, ub, dim, fobj)
Position = initialization(N, dim, ub, lb);
Fitness = zeros(N, 1);
epsilon = 1e-6;
alphabet = 1 : N;
%% Record the initial optimal solution and fitness
for i = 1:N
Fitness(i) = fobj(Position(i,:));
end
[~, Ind] = sort(Fitness);
Best_Score = Fitness(Ind(1));
Best_Pos = Position(Ind(1),:);
CG_curve = zeros(1, Max_iter);% Store convergence information
%% Main optimization loop
for it = 1:Max_iter
delta = sin(pi/2 * (1 - (2*it / Max_iter)).^5); % eq.(12)
a = (1 - it/Max_iter) * rand(1, dim);
for i = 1:N
rr1 = rand;rr2 = rand;
if rr1 >= rr2
Pr = (Fitness.^2)/((norm(Fitness)^2));
P = randsrc(1, 2, [alphabet; Pr']);
P1 = P(1);P2 = P(2);
else
P = Ind(1:2);
P1 = P(1);P2 = P(2);
end
r = rand;
J = Get_jacobian(fobj, Position(P1, :), epsilon); % Generalised Jacobi matrix
if 3*rand >= 2*rand
% eq.(14)
grad = (r * (Position(P1, :) - Best_Pos) + (1-r) * (Position(P2, :) - Best_Pos)) / 2;
pos_n1 = Position(i,:) - delta * grad;
else
% eq.(15)
grad = (r * (Position(P2, :) - Best_Pos) + (1-r) * (Position(P1, :) - Best_Pos)) / 2;
pos_n1 = Position(i,:) + delta * J * grad';
end
newpos1 = max(min(pos_n1, ub), lb);
fitt = fobj(newpos1);
if fitt < Fitness(i)
Fitness(i)= fitt;
Position(i,:) = newpos1;
end
if rand > rand
P = randperm(N, 2); % eq.(13)
P1 = P(1);P2 = P(2);
if 3*rand >= 2*rand
% eq.(14)
grad = (r * (Position(P1, :) - Best_Pos) + (1-r) * (Position(P2, :) - Best_Pos)) / 2;
pos_n2 = Position(i,:) - delta * grad;
else
% eq.(15)
grad = (r * (Position(P2, :) - Best_Pos) + (1-r) * (Position(P1, :) - Best_Pos)) / 2;
pos_n2 = Position(i,:) + delta * J * grad';
end
newpos2 = max(min(pos_n2, ub), lb);
fitt = fobj(newpos2);
if fitt < Fitness(i)
Fitness(i)= fitt;
Position(i,:) = newpos2;
end
end
for j = 1 : dim
r1 = 1+rand;r2 = 1+rand; % eq.(16)
pho_1 = r1 * Position(i, :) + (1-r1) * Best_Pos + r2 * (Position(i, :) - Best_Pos); % eq.(17)
pho_2 = Position(i,:) + a.* (newpos1 - Best_Pos); % eq.(18)
pos_n3 = Position(i,:);
if rand/j > rand
pos_n3(j) = pho_1(j);
else
pos_n3(j) = pho_2(j);
end
newpos3 = max(min(pos_n3, ub), lb);
fitt = fobj(newpos3);
if fitt < Fitness(i)
Fitness(i)= fitt;
Position(i,:) = newpos3;
end
end
end
if rand <= 1/2*(tanh(9*it/Max_iter-5)+1)
pos_n4 = zeros(1, dim);
d=rand()*(1-it/Max_iter)^2;
Step_length=levy(N, dim,1.5);
Elite=repmat(Best_Pos, N, 1);
r=rand;
for i=1:N
for j=1:dim
pos_n4(j)=r*Elite(i,j)+(1-r)*Step_length(i,j)*d*...
(Elite(i,j)-Position(i,j)*(2*it/Max_iter)); % eq.(21)
end
newpos4 = max(min(pos_n4, ub), lb);
fitt = fobj(newpos4);
if fitt < Fitness(i)
Fitness(i) = fitt;
Position(i,:) = newpos4;
end
end
end
%% Record convergence curve
[~, Ind] = sort(Fitness);
if Fitness(Ind(1)) < Best_Score
Best_Score = Fitness(Ind(1));
Best_Pos = Position(Ind(1),:);
end
CG_curve(it) = Best_Score;
end
end
% Finite difference method for approximating generalised Jacobi matrix
function J = Get_jacobian(fobj, x, epsilon)
% f: handle to target function, accepts vector x
% x: current point (vector)
% epsilon: small perturbation value
n = length(x);
fx = fobj(x);
m = length(fx);
J = zeros(m, n);
% Calculate the finite difference in each direction according to eqs. (9) and (10).
for i = 1:n
x_perturbed = x;
x_perturbed(i) = x_perturbed(i) + epsilon;
f_perturbed = fobj(x_perturbed);
J(:, i) = (f_perturbed - fx) / epsilon;
end
end
function [z] = levy(n,m,beta)
% beta is set to 1.5 in this paper
num = gamma(1+beta)*sin(pi*beta/2);
den = gamma((1+beta)/2)*beta*2^((beta-1)/2);
sigma_u = (num/den)^(1/beta); % eq.(20)
u = random('Normal',0,sigma_u,n,m);
v = random('Normal',0,1,n,m);
z =u./(abs(v).^(1/beta));
end
% Initialization function
function X = initialization(N, Dim, UB, LB)
B_no = size(UB, 2); % number of boundaries
if B_no == 1
X = rand(N, Dim) .* (UB - LB) + LB;
end
% If each variable has a different lb and ub
if B_no > 1
X = zeros(N, Dim);
for i = 1:Dim
Ub_i = UB(i);
Lb_i = LB(i);
X(:, i) = rand(N, 1) .* (Ub_i - Lb_i) + Lb_i;
end
end
end参考文献
[1] Yu D, Ji Y, Xia Y. Projection-Iterative-Methods-based Optimizer: A novel metaheuristic algorithm for continuous optimization problems and feature selection[J]. Knowledge-Based Systems, 2025: 113978.
完整代码获取
底部卡片获取代码





















 229
229

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










