Brief Bioinform | 农科院深圳基因组所王怡雯组提出一种去除微生物组数据中批次效应的多元算法框架...-CSDN博客

PLSDA-batch：去除微生物组数据中批次效应的多元算法框架

PLSDA-batch: a multivariate framework to correct for batch effects in microbiome data

Article，2023-1-18，Briefings in Bioinformatics，[IF 13.994]

DOI：https://doi.org/10.1093/bib/bbac622

原文链接：https://academic.oup.com/bib/article/24/2/bbac622/6991121?login=false

第一作者：Yiwen Wang (王怡雯)

通讯作者：Kim-Anh Lê Cao

主要单位：

农科院深圳基因组研究所 (Shenzhen Branch, Guangdong Laboratory of Lingnan Modern Agriculture, Genome Analysis Laboratory of the Ministry of Agriculture and Rural Affairs, Agricultural Genomics Institute at Shenzhen, Chinese Academy of Agricultural Sciences, 97 Buxin Rd, Shenzhen, 518000, Guangdong, China)

墨尔本大学数学与统计学院 (Melbourne Integrative Genomics, School of Mathematics and Statistics, The University of Melbourne, 30 Royal Parade, Melbourne, 3052, VIC, Australia)

- 摘要 -

微生物组数据对环境变化敏感，极易受到批次效应（与实验因素无关的差异来源）的影响，从而掩盖了数据中实验因素引起的差异。现有的批次效应校正方法主要是为基因表达量数据开发的，没有考虑到微生物组数据的固有特征，包括零膨胀、过度离散和变量之间的相关性。为了针对微生物组数据进行有效的批次效应校正，我们开发了一种基于偏最小二乘判别分析（PLSDA）的多元非参数批次效应去除法：PLSDA-batch。它能够分别估算实验和批次效应相关的潜在组分，然后去除批次效应组分；同时开发了两种延伸方法来应对不平衡的实验设计和过拟合的现象，并将我们的方法与目前处理批次效应几种主流的方法进行比较，即removeBatchEffect、ComBat 和SVA，并在模拟数据集和三个实际数据集中使用各种指标和可视化方法进行评估。结果表明，我们的三种方法在去除批次差异时，在保留实验差异方面具有较好的表现，尤其是对于不平衡的实验设计。

- 引言 -

研究微生物组成和表型（包括人类疾病）之间的联系是微生物组研究的主要目标，例如，肠道微生物群落的破坏与多种疾病和亚健康状态有关，从炎症性肠病、糖尿病、到肥胖和营养不良。然而，由于微生物群落是高度动态的，因此微生物组数据极易受到批次效应的影响，批次效应通常掩盖了研究人员所感兴趣的生物学效应。因此，处理批次效应对于提高微生物组研究的有效性至关重要。我们开发了一种基于偏最小二乘判别分析（PLSDA）的多元非参数批次效应去除法。PLSDA-batch非常适合微生物组数据，因为它是非参数、多元且可视化的。通过估计与实验效应和批次效应相关的潜在组分，可以去除数据中的批次差异，并保留感兴趣的生物学差异。同时为了针对不平衡的实验设计和模型过拟合现象，我们提出了另外两种延伸方法。我们在大量的模拟数据集和三个实际数据集中评估了PLSDA-batch的效率，同时将我们的方法与以往应用于微生物研究的主流线性方法，例如ComBat和removeBatchEffect进行了比较，主要集中在比较去除批次效应和揭示实验效应的效率方面。由于我们的方法与SVA有一些相似之处，即使SVA仅仅是一种控制而非去除批次效应的方法，我们也在模拟数据集中进行了一些比较。

- 结果 -

我们先在模拟数据集上测试了PLSDA-batch，并与常用的removeBatchEffect、ComBat和SVA这三种方法进行了比较；然后在三个实际数据集上，将removeBatchEffect、ComBat这两种方法与我们的方法进行了对比。

模拟研究

pRDA 评估

高效的批次效应校正方法应该能够产生不含有批次效应的数据，即由批次效应解释的方差比例为零，并且与原始数据相比，由实验效应解释的方差比例应该更大，正如图1A中所示原始数据和基准数据（只含有实验效应）。

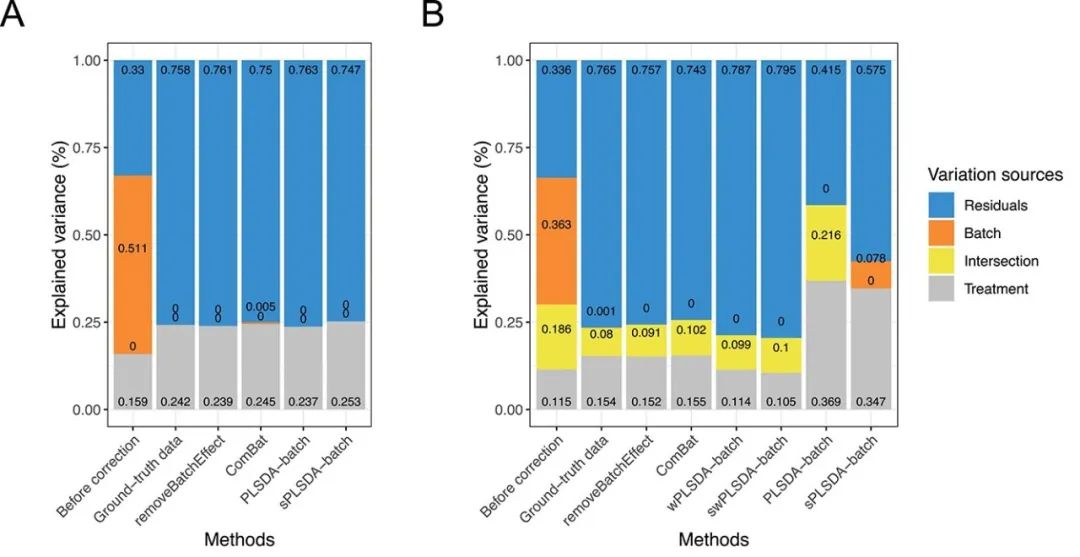
图1：模拟数据集（两个批次组）：

比较批次效应校正前后的解释方差，针对（A）平衡和（B）不平衡的实验设计。pRDA方法估计了由（从上到下）残差、批次效应、批次和实验共同解释以及实验效应解释的方差比例。

对于平衡的实验设计，实验效应和批次效应之间不应存在共同解释的方差，与图中观察结果一致。所有方法成功地去除了批次效应并保留了（或稍微增加了）实验效应（sPLSDA-batch），除了ComBat方法，经该方法处理的数据仍然存在部分批次效应。

批次效应和实验效应之间共同解释的方差越大，实验设计越不平衡，由此可见，（图1B）是极其不平衡的实验设计。这部分方差在基准数据中也存在，但相比未校正的数据较小。对于这种实验设计，未加权的PLSDA-batch和sPLSDA-batch表现不佳，对于PLSDA-batch，共同解释的方差增加，而对于sPLSDA-batch，批次方差无法完全去除。其他方法成功地去除了批次方差，removeBatchEffect和ComBat方法解释的实验方差比例相较于wPLSDA-batch和swPLSDA-batch解释的实验方差略高一些。

R²评估

我们采用R²值估算每个变量的实验和批次效应解释的方差比例。在平衡的实验设计中（图2A）、removeBatchEffect和PLSDA-batch表现最好，结果与基准数据非常相似。ComBat处理后的数据残留了更多批次效应方差，体现在数据模拟时仅加入批次效应的变量和同时加入批次和实验效应的变量上，表明批次效应去除得不完全，这与之前描述的整体pRDA评估结果一致。对于sPLSDA-batch，数据模拟中未加入实验效应的变量（仅含有批次效应）包含了轻微的（虚假的）实验方差，这也和pRDA的评估结果吻合。然而，当模拟数据中没有包含同时具有批次和实验效应的变量时，sPLSDA-batch与PLSDA-batch的表现很好。

而在不平衡的实验设计中，removeBatchEffect和ComBat具有相似的效果（图2B）。使用 wPLSDA-batch和swPLSDA-batch，与基准数据相比，数据模拟时具有实验效应和批次效应的变量在校正后解释了较少的实验方差。然而，对于其他变量，wPLSDA-batch及其sparse版本的表现与基准数据相似。

图2：模拟数据集（两个批次组）：

（A）平衡和（B）不平衡的实验设计的批次效应校正前后每个微生物变量的R²值。每个箱线图表示模拟数据中具有相应效应（批次或/和实验效应）的同类变量的R²值。每个R²都是从单因素方差分析中计算获得的，以实验效应或批次效应作为协变量（x轴），颜色表示分配给每个变量的效应。

准确性测量

准确性测量与变量选择相结合的结果突出了去除批次效应的重要性，因为与原始数据相比，F1 分数和 AUC 都有很大改善（表3）。

表 3：模拟数据集（两个批次组）：批次效应校正前后精度测量的结果总结。

使用Precision、Recall、F1 分数（使用单因素方差分析作为变量选择方法）和 AUC（使用 sPLSDA 作为变量选择方法）评估正确识别的具有实验效应的微生物变量的比例。每个值都是50次重复的平均值（或标准差）。

在实验设计平衡的数据集中，将原始数据与基准数据相比，选择的具有实验效应的变量具有更高的Precision、更低的Recall和更低的AUC，表明从原始数据中能选择出的具有实验效应的变量数量相较于不含批次效应的基准数据更少。结合单因素方差分析，SVA表现最好，测量精度最高，有时甚至比基准数据更高，其他方法也达到了类似的效果。虽然sPLSDA-batch比其他方法产生了更多的第一类错误，即假阳性，但PLSDA-batch校正后的数据得到的AUC比其他方法略好。

在实验设计不平衡的数据集中，SVA的精度较低且与原始数据非常相似，表明 SVA的表现严重依赖于实验设计并且容易过拟合。这或许可以解释 SVA 在平衡数据中过于“优秀”的效果，而wPLSDA-batch表现最好，结果接近于基准数据。

模拟数据测试结果总结

大量的模拟研究显示，与非加权的PLSDA-batch相比，加权的版本对于不平衡的实验设计是必要的。虽然PLSDA-batch与其他批次效应校正方法相比，保留的实验方差比例相似或略小，但在实验设计不平衡的情况下，有更高的F1得分和AUC。当模拟数据中没有同时具有实验效应和批次效应的变量时，sPLSDA-batch和PLSDA-batch校正后的数据接近基准数据。然而，当模拟数据含有同时包括这两种效应的变量时，sPLSDA-batch的效果略差于PLSDA-batch。此外我们的结果还表明，SVA有过拟合数据的倾向，而ComBat无法完全消除批次差异，removeBatchEffect无法保留足够的实验效应以准确识别变量。

实例研究

主成分分析

在Sponge数据中（图4A），不同组织样本（生物学效应）之间的差异主要体现在第一主成分上，而第一主成分解释了总数据方差的24%。批次差异主要体现在第二主成分上，而第二主成分解释了总数据方差的21%。因此，在这项研究中，批次效应小于实验效应。批次效应校正后，批次之间的差异变得几乎观测不到（图4B-E），但是ComBat校正后的数据，在Choanosome组织中仍然可以观察到两批次的样本存在明显差异。此外，第一主成分（实验效应）解释的方差在所有校正后的数据中都增加了，而PLSDA-batch和 sPLSDA-batch生成了仅次于 ComBat (28%) 的第二高的方差比例 (27%) .

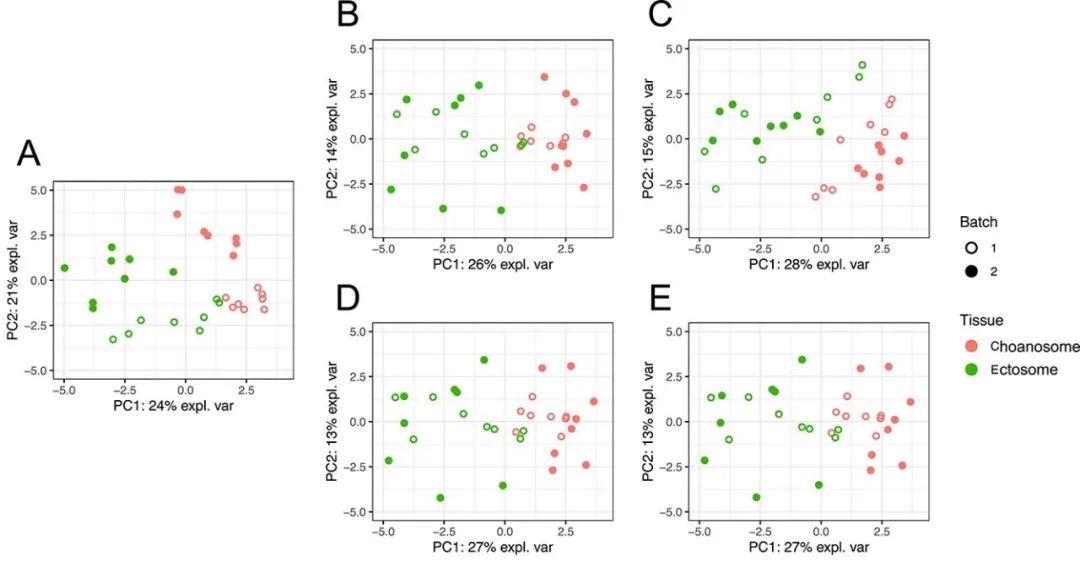
图4：（A）表示校正前的Sponge数据，接着分别使用（B） removeBatchEffect、（C） ComBat、（D） PLSDA-batch 和（E）sPLSDA-batch方法进行批次效应校正，并得到相应的PCA 样本图。颜色代表不同的组织类型（实验效应），形状代表了批次类型。

在AD数据中（图5），所有方法都成功去除了批次差异。其中，PLSDA-batch表现最好，因为与实验效应高度相关的第一个主成分解释的方差比例大于其他任一方法的解释方差。

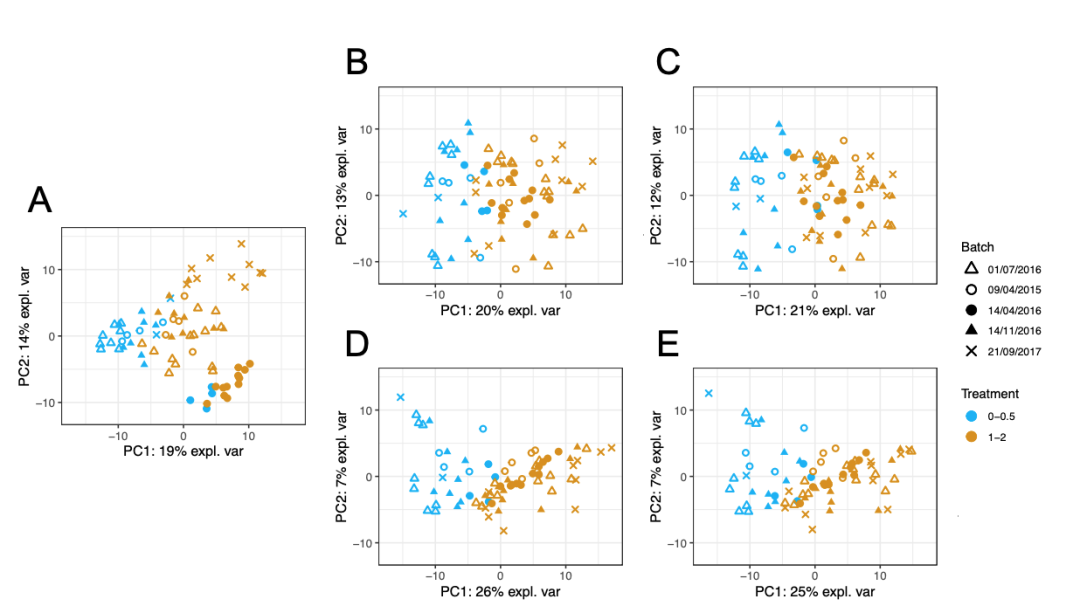
图5: （A）表示校正前的AD数据，接着分别使用（B） removeBatchEffect、（C） ComBat、（D） PLSDA-batch 和（E）sPLSDA-batch方法进行批次效应校正，并得到相应的PCA 样本图。颜色代表不同的实验类型（实验效应），形状代表了批次类型。

在HFHS数据中，PCA图表明批次差异仅在一个实验组中观察到并且非常弱（图6）。批次效应校正后，批次差异被移除，第一个主成分（与实验效应相关）解释的方差比例略有改善，表明实验效应仍然存在。该案例研究表明，当批次效应非常弱时，去除批次效应的方法仍然适用。然而，sPLSDA-batch 表现最差，实验方差丢失，表明该方法不适合校正非常弱的批次效应。

图6: （A）表示校正前的HFHS数据，接着分别使用（B） removeBatchEffect、（C） ComBat、（D） PLSDA-batch 和（E）sPLSDA-batch方法进行批次效应校正，并得到相应的PCA 样本图。颜色代表不同的饮食类型（实验效应），形状代表了批次类型。

Alignment Scores

通常，当难以在PCA图上评估去除批次效应的效果时，Alignment Scores可以用来补充解释PCA结果。于是在图7中，我们观察到与原始数据相比，不同批次的样本经过不同方法的校正后混合得更好。

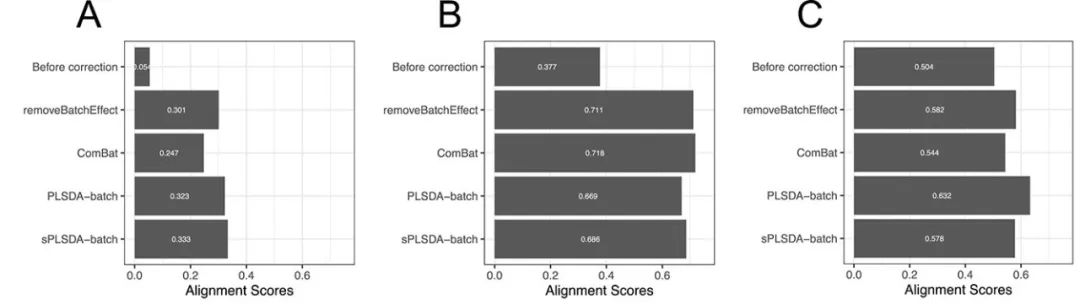
图7：使用不同方法对（A）Sponge数据、（B）AD数据和（C）HFHS数据进行批次效应校正前后的Alignment Scores。由于Alignment Scores是基于PCA的距离矩阵计算得到的，因此较大的Alignment Scores表明来自不同批次的样本得到了更好的混合。只有当样本在其PCA映射中具有相似的样本分布时，才能比较方法之间的Alignment Scores，即Sponge数据和HFHS数据。

在Sponge数据中，使用PLSDA-batch和sPLSDA-batch校正的数据比使用removeBatchEffect和ComBat校正的数据具有更高的Alignment Scores，表明在去除批次方面具有更好的效果。ComBat校正后的数据具有最低的Alignment Scores，这与PCA一致，即数据中仍然残留批次差异。

在AD数据中，使用PLSDA-batch和sPLSDA-batch校正后数据的Alignment Scores表现出比用removeBatchEffect和ComBat校正后更差的效果。这可能是由于PCA映射的差异导致的，因为Alignment Scores的计算会用到PCA的映射矩阵。使用removeBatchEffect和ComBat校正的数据通过PCA映射后具有较大的方差，而PLSDA-batch和 sPLSDA-batch校正的数据方差则较小，因此会产生较小的Alignment Scores，因为更容易将同批次的样本定位为相邻样本。事实上，下面pRDA的评估结果证实了PLSDA-batch和sPLSDA-batch都完全去除了批次差异。

对于 HFHS 数据中的弱批次效应，PLSDA-batch与其他方法相比表现最佳，Alignment Scores最高。我们没有遇到与AD数据相同的问题，因为PCA映射后的样本分布在所有数据中都相似。

pRDA评估

接下来，我们主要使用pRDA估计批次效应校正后数据的整体实验和批次效应解释的方差比例。

在Sponge数据中（图8A），不同的方法保留了相似比例的实验方差（removeBatcheffect：17.5%，ComBat：18.2%，PLSDA-batch：18.2%，sPLSDA-batch：18.2%）并去除了所有批次方差，除了ComBat，它仍保留了 0.9% 的批次差异。

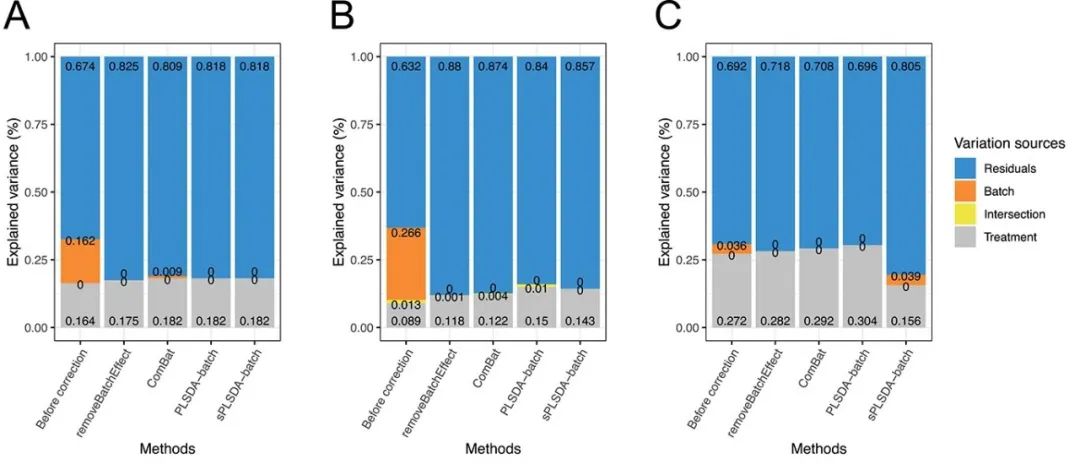
图8: （A）Sponge数据、（B）AD数据和（C） HFHS数据去除批次效应前后的解释方差。

在AD数据中（图8B），观察到由于实验设计不平衡导致的少量共同解释的方差 (1.3%)。由于共同解释的部分很小，未加权的PLSDA-batch和sPLSDA-batch仍然适用，因此在这未使用加权版本。相较于其他方法，PLSDA-batch保留的由实验效应解释的方差比例最大，以及最大比例的共同解释方差。sPLSDA-batch校正后的数据比另外两种单变量方法校正后的数据有更高比例的实验方差。sPLSDA-batch是PLSDA-batch的sparse版本，因此sPLSDA-batch 保留的实验方差比例应该与PLSDA-batch相比几乎相同或略小，也正如我们在本研究中观察到的那样。

在批次效应较弱的HFHS数据中，我们检测到3.6%的由批次效应解释的方差（图8C）。PLSDA-batch效果最好，因为校正后的数据保留了最高比例的实验方差并完全去除了批次方差。sPLSDA-batch表现最差，因为该方法没有去除足够的批次方差并丢失了一部分实验方差。这一结果与之前的结果一致，即 sPLSDA -batch校正后的数据与其他方法相比，具有较低的Alignment Scores（与批次差异相关）和由第一个PCA主成分解释的方差较低（与实验差异相关）。

- 讨论 -

在本文中，主要介绍了一种以多元方式去除批次效应，同时保留实验差异的方法，称之为PLSDA-batch。除此之外，我们还提出了两种延伸方法：1）加权PLSDA-batch应对不平衡的实验设计，2）Sparse PLSDA-batch应对模型过拟合现象。在本文中，将微生物组数据称为微生物分类学数据（metataxonomic data），分析的是OTU级别的数据。然而，本文所提出的方法也适用于任何其他分类级别的微生物数据以及宏基因组数据。

根据分析的结果，我们提出以下标准来选择批次效应去除的最佳方法：1）当批次效应校正后的实验方差比例大于原始数据时，最好选择能保留较小实验方差的方法，因为该实验方差更倾向于不是虚假的；2）相反，当校正后的实验方差所占比例小于原始数据时，最好选择保留较大实验方差的方法。

我们方法的局限性在于需要预定义批次组信息。如果批次信息未知，建议采用数据导向的批次分类，例如PCA或其他聚类方法识别的批次分类。虽然wPLSDA-batch表现出良好的效果，但在微生物变量中，批次和实验之间存在的相互作用仍然难以通过某种算法分开，很可能是因为这种相互作用是非线性的。当批次效应和实验效应共线时，目前只考虑批次效应但不对其进行校正的方法才是最合适的，例如线性回归。此外，PLSDA方法是线性算法，其中解释组分和响应组分均基于变量的线性组合构建，并且组分之间也是通过线性关系来建模的。而微生物组数据中的变量间的关系很可能是非线性的，因此，这种非线性的拟合可以在未来通过将本文的方法架构于非线性的PLS kernel算法来实现。

参考文献

Yiwen Wang, Kim-Anh Lê Cao, PLSDA-batch: a multivariate framework to correct for batch effects in microbiome data, Briefings in Bioinformatics, Volume 24, Issue 2, March 2023, bbac622, https://doi.org/10.1093/bib/bbac622

- 作者简介 -

第一作者

中国农科院深圳农业基因组研究所

王怡雯

副研究员

王怡雯，副研究员，硕士生导师，食品科学研究中心Pre-PI。2022年获得墨尔本大学生物统计学博士学位。研究专长为针对生物学问题分析和可视化数据，同时开发针对微生物组数据分析的统计和计算方法，开发了PLSDA-batch等算法软件包。以第一作者在Briefing in Bioinformatics，Annals of the Rheumatic Diseases 等期刊发表学术论文多篇。主持中国农业科学院博士后国际交流计划引进项目、中国博士后科学基金站前特别资助、面上项目、国家自然科学基金青年科学基金项目等基金。

通讯作者

墨尔本大学

Kim-Anh Lê Cao

研究员

Kim-Anh Lê Cao，于2008年毕业于法国图卢兹大学，获博士学位。随后，前往澳大利亚昆士兰大学(University of Queensland)攻读博士后，并被聘为QFAB Bioinformatics的研究和咨询生物统计分析师。2014年在昆士兰大学Diamantina研究所期间，Kim-Anh Lê Cao的研究方向转向了生物医学问题。2017年，她加入墨尔本大学数学与统计学院和墨尔本综合基因组学研究院。Kim-Anh Lê Cao是NHMRC的职业发展研究员，也是澳大利亚科学院2019年莫兰奖章的获得者。与此同时，还是是多元统计方法的专家，并开发了“组学数据整合”的新方法。自2009年以来，她的团队一直致力于开发R工具包mixOmics，致力于“组学”数据的整合分析，以帮助研究人员挖掘和理解生物数据。

10000+：菌群分析宝宝与猫狗梅毒狂想曲提DNA发Nature

系列教程：微生物组入门 Biostar 微生物组宏基因组

专业技能：学术图表高分文章生信宝典不可或缺的人

一文读懂：宏基因组寄生虫益处进化树必备技能：提问搜索 Endnote

扩增子分析：图表解读分析流程统计绘图

16S功能预测 PICRUSt FAPROTAX Bugbase Tax4Fun

生物科普: 肠道细菌人体上的生命生命大跃进细胞暗战人体奥秘

写在后面

为鼓励读者交流快速解决科研困难，我们建立了“宏基因组”讨论群，己有国内外6000+ 科研人员加入。请添加主编微信meta-genomics带你入群，务必备注“姓名-单位-研究方向-职称/年级”。高级职称请注明身份，另有海内外微生物PI群供大佬合作交流。技术问题寻求帮助，首先阅读《如何优雅的提问》学习解决问题思路，仍未解决群内讨论，问题不私聊，帮助同行。

点击阅读原文，跳转最新文章目录阅读

https://mp.weixin.qq.com/s/5jQspEvH5_4Xmart22gjMA