深度模型（GAN的扩展）提出一种基于贝叶斯方法的数据扩展方法

一、总览

在进行深度学习的时候，不管是分类还是识别，都需要大量的数据集，为了解决数据集稀少的问题，我们可以通过各种数据集增强的方式来增强模型的鲁棒性。
在这之前我们用到了传统的数据增强方式，比如：图像旋转，图像翻转，仿射变换，噪声添加，图像色彩干扰等各种方法（详情请看），先如今我们来使用GAN（基于贝叶斯方法）来增强数据
论文：https://papers.nips.cc/paper/6872-a-bayesian-data-augmentation-approach-for-learning-deep-models.pdf

数据增强的过程自动生成新的带注释的训练样本。通过应用于带注释训练样本的随机几何或外观变换来获得新的训练样本，

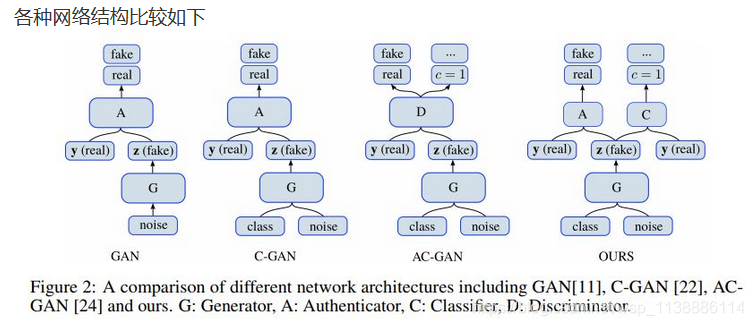
数据扩展方法整体流程如下：

二、深度学习中的数据增强算法

Bayesian Neural Networks

我们的目标是使用注释的训练集来估计深度学习模型的参数。记为 Y = { y n } n − 1 N \mathcal{Y} = \{\rm y_n\}_{n-1}^N Y={yn​}n−1N​ ，当 $\mathrm{y}=(\mathrm{t},\mathrm{x})$, t ∈ { 1 , 2 , . . . , K } ( K ≠ C l a s s e s ) t \in \{1,2,...,K\} (K\neq \rm Classes) t∈{1,2,...,K}(K̸​=Classes) 数据集表示为 $\mathrm{x}\in {\mathbb{R}}^{\mathrm{D}}$，模型参数为 $\theta$。训练过程的优化问题定义如下：
$${\theta }^{\ast }=\text{arg}\underset{\theta }{\max }\log p(\theta |y)$$

由于 $p(\theta |y)=p(\theta |t,x)\propto p(t|x,\theta )p(x|\theta )p(\theta )$
假设数据样本$\mathcal{Y}$是条件独立的，最大化的代价函数定义为：
$$\log p(\theta |\text{y})\approx \log p(\theta )+\frac{1}{N}\sum _{n-1}^N(\log p(t_n|{\text{x}}_n,\theta )+\log p({\text{x}}_n|\theta ))$$

优化函数

在本文中，我们提出了一种新的贝叶斯DA，改进了深度学习分类模型训练进程。与目前主要的对观测到的训练样本应用随机变换的方法不同，我们的方法在理论上是合理的；缺失的数据是从从带注释的训练集学习的分布中采样的。然而，我们不训练生成分布独立于训练的分类模型。相反，两个模型都是基于我们提出的贝叶斯DA公式联合优化的，该公式将统计学习中的经典潜变量方法与现代深生成模型联系起来。我们的数据增强方法的优点在几个图像分类任务得到验证。

项目地址;
https://github.com/toantm/keras-bda
https://github.com/lukedeo/keras-acgan