二、大模型原理：图文解析Transformer原理与代码-CSDN博客

本文链接：https://blog.csdn.net/ngadminq/article/details/147687050

Transformer是很多大模型的基石，也是现在llm面试岗位必考的。
即使是ChatGPT中的"T"也代表着Transformer。以下模型都是Transformer的演变模型（当然每个大模型的Transformer都可能存在差别）：
在这里插入图片描述

本文将从原理+实战带你深入理解Transformer

Transformer结构

先放出整体架构，后文的1~4点都是对原件进行深入探讨的。
在这里插入图片描述
从总体上来看
可以将Transformer看为是N个编码结构和N个解码结构的模型，这里的解码/编码结构即为后文解释的 Transformer Block；

上图的inputs其实是输入的embedding向量+位置编码向量。

1. Token Embedding：从符号到向量的转换

上一小节我们已经讲述了一句话是如何转为数值表达的，但对于计算机而言仅仅是一个个数值是没有语义信息的。

Token本质上是符号：

"Apple"是一个符号
"Cat"是一个符号
"Run"是一个符号
"Jump"是一个符号

虽然我们知道"Run"和"Jump"都是动词，它们在语义上比"Cat"和"Apple"更相近，但从Token的角度看，它们都只是独立的符号，彼此之间没有任何关联。

实现机制：查表法

Transformer中的Token嵌入采用查表法：

维护一个包含所有可能Token及其对应向量的表格
对于每个输入Token，在表中查找其对应的向量
这些向量是模型的可学习参数，在训练过程中自动优化

2. 位置编码：为序列添加位置信息

需要位置编码原因可以回想一下RNN，对RNN而言是用的一套参数。
而Transformer的输入是一起扔给模型的，因此就缺少了先后位置关系，从而使用了位置编码。

假设没有位置编码，同一个Token总是有相同的向量表示，那么模型将会丧失了对上下文的信息保留。例如：

“Bank”（银行）在"I went to the bank"中
“Bank”（河岸）在"I sit by the river bank"中
这两个"bank"使用相同的Token Embedding，但含义完全不同，保留了位置信息为下面的多头注意力机制保留了所含有的信息。

位置编码的实现方式

1. 人工设计的位置嵌入

最早的Transformer实现中，位置编码是人工设计的，采用以下方式：
使用正弦和余弦函数为每个位置生成独特的编码
在这里插入图片描述
简单来说就是偶数位为sin，奇数位为cos。

2. 可学习的位置嵌入

位置编码也可以通过训练学习

3. 注意力机制（Attention）

通过注意力机制增加了语义的理解，解决了歧义问题（如"bank"指银行还是河岸）

如果你能记住下面这句话，就记住了注意力的本质：
👉 输入一排词向量 → 为每个词找到重要上下文 → 得到新的词向量
在这里插入图片描述
为每个词找到重要上下文，这部分即是量化了句子中任意两个词条之间的依赖关系。如下图将会去对输入句子做比较，即每个词之间又会对句子中所有词做比较

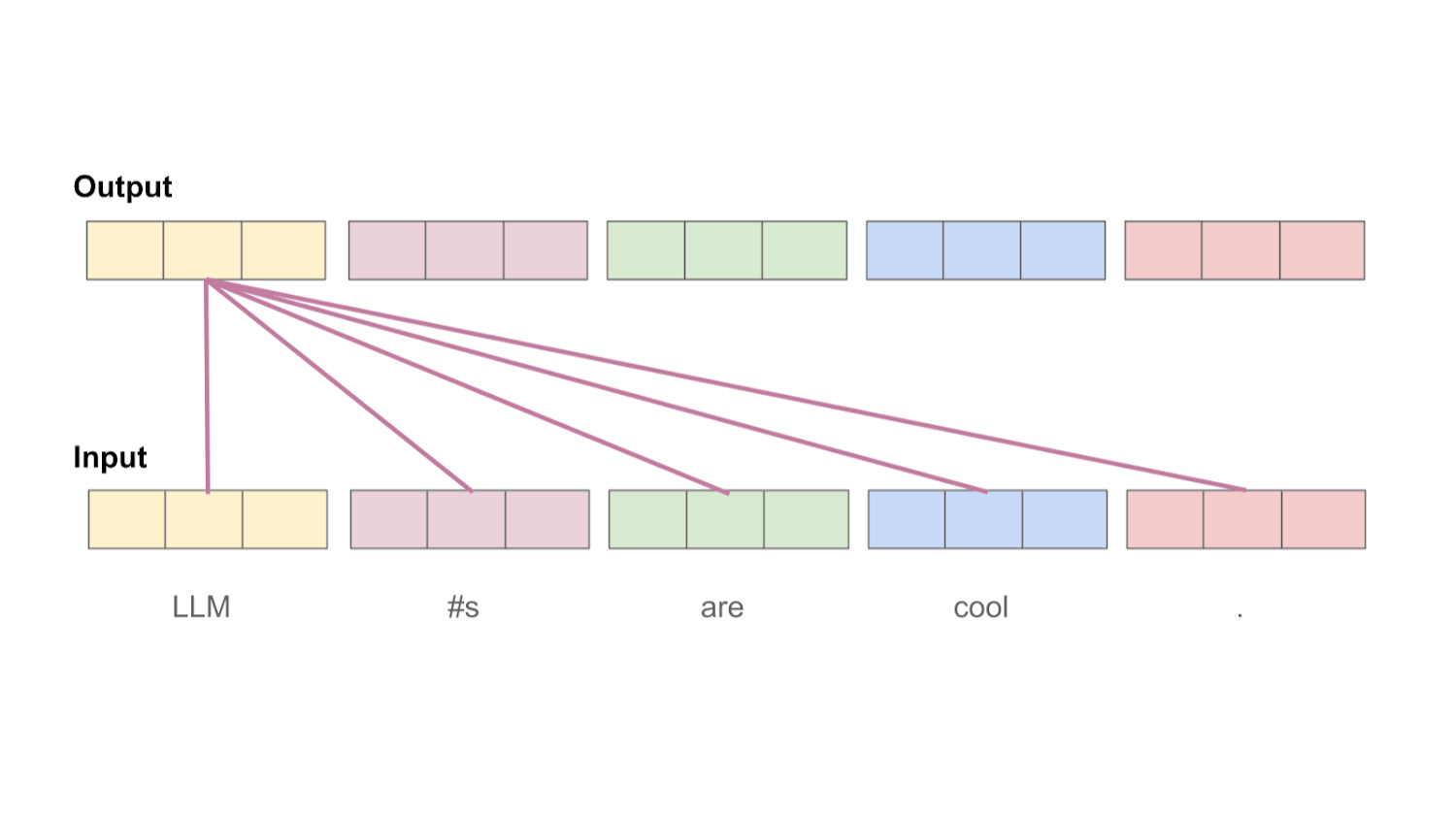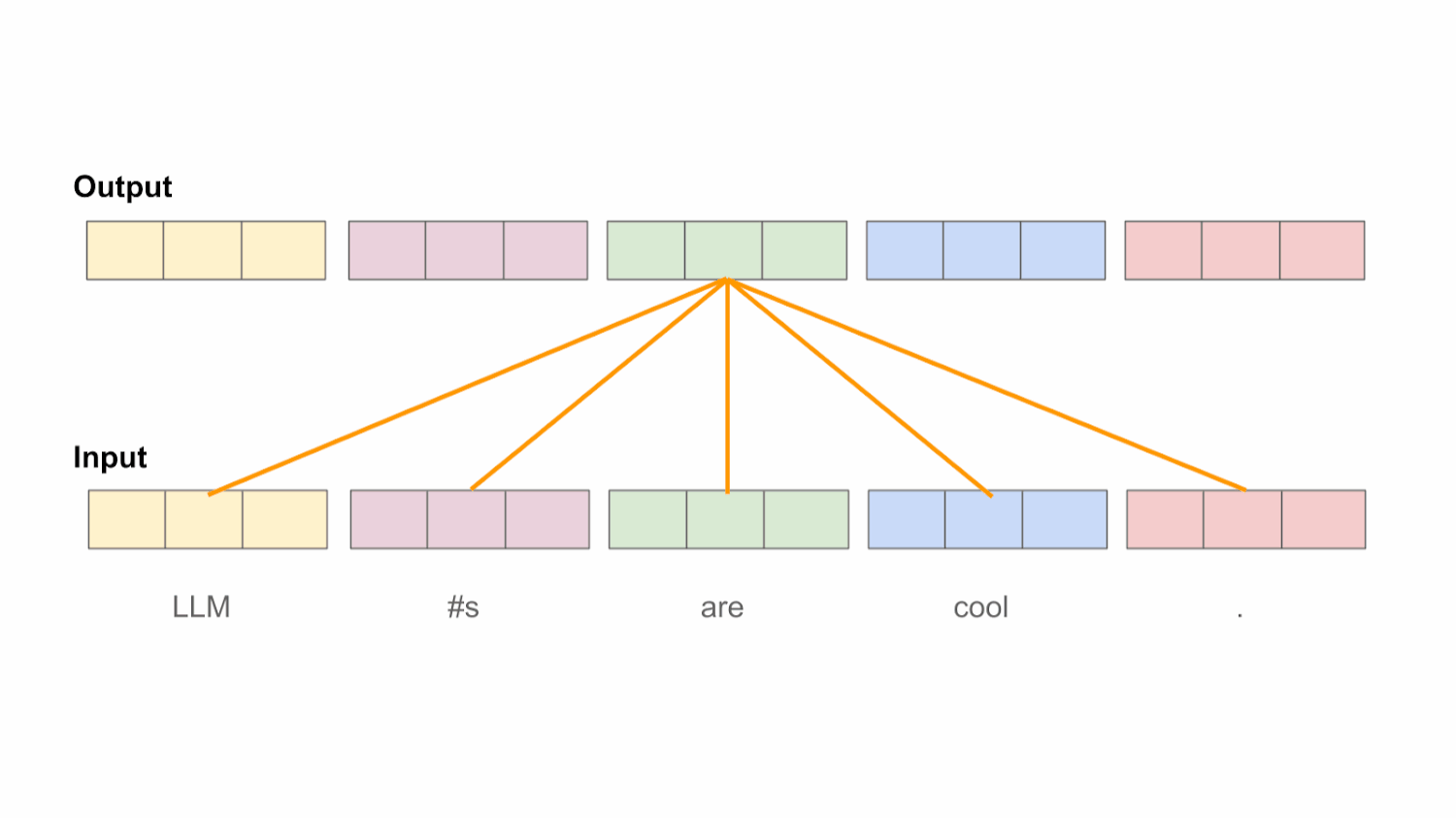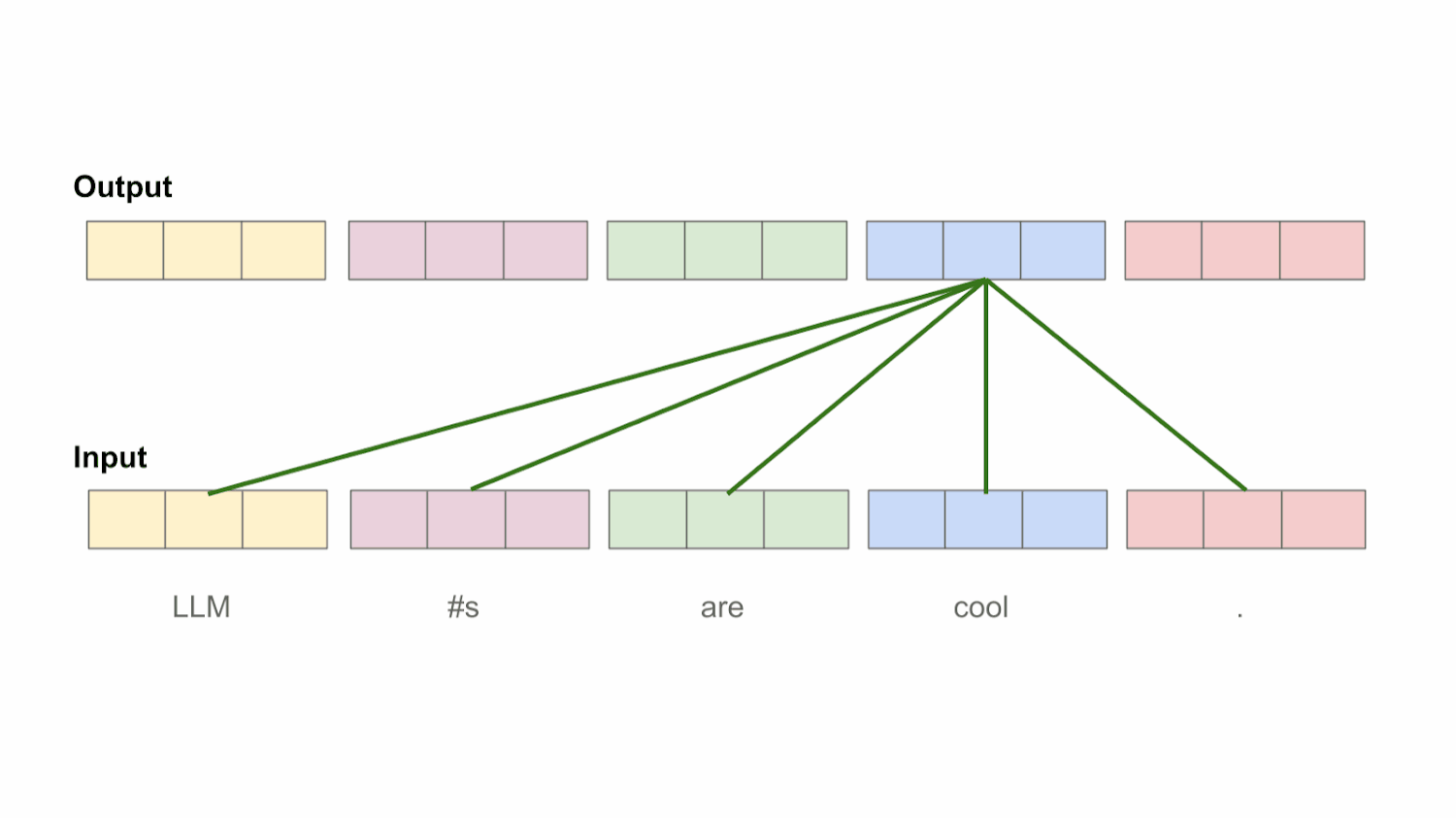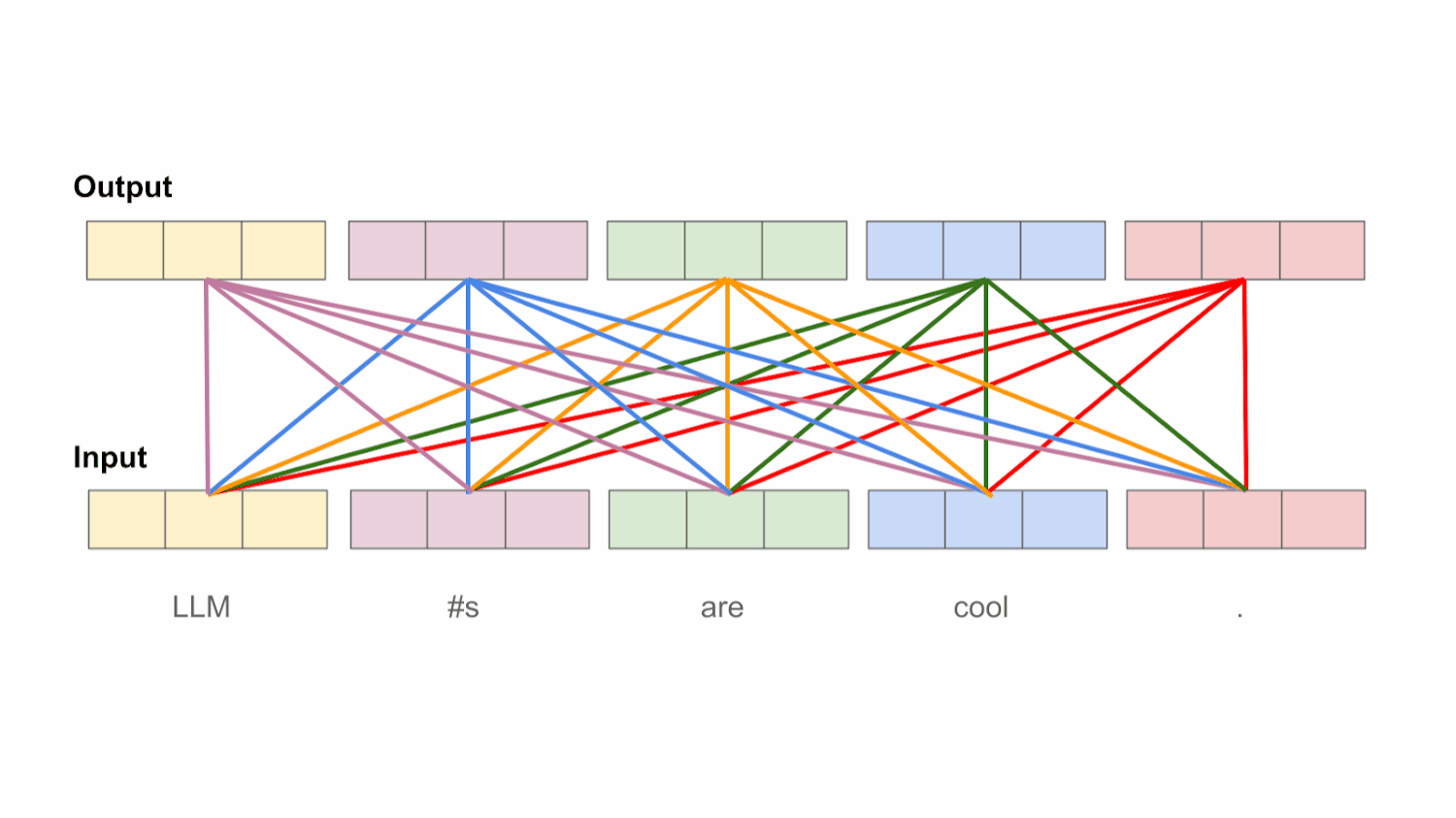
注意力机制QKV理解

注意力机制中最重要概念即对下图公式的理解
在这里插入图片描述

经过embedding+位置编码作为输入，我们的对模型的输入是个 $[B, T, d]$ 矩阵。其中批次大小为 $B$ ，每个序列长度为 $T$ ，每个词元向量的维度为 $d$ ，也就是自注意力层接收的输入张量形状就是 $[B, T, d]$ 。
为了简化说明，我们先将B设置为1，也就是单个词元序列作为输入来讲解自注意力的计算过程（见下图），但相同的原理可以很容易地扩展到多个序列组成的批次上。
在这里插入图片描述
QKV创建
可以看到该公式引入了三个矩阵QKV，这些矩阵来自于输入序列中的token向量，经过了三次独立的（线性）投影，形成Q、K和V矩阵。
这

以输入 [“LLM”, “#s”, “are”, “cool”]为例，每个词通过嵌入层和线性投影后得到Query向量和Key向量。
为了简化，我们假设每个向量是3列组成的（也就是head_size,这是一个由开发者决定的超参数，控制了QKV矩阵的维度，即注意力头大小)：

embeddings = [
    [0.1, 0.2, 0.3],  # "LLM"的嵌入
    [0.4, 0.5, 0.6],  # "#s"的嵌入
    [0.7, 0.8, 0.9],  # "are"的嵌入
    [1.0, 1.1, 1.2]   # "cool"的嵌入
]

投影为Query和Key矩阵
现在，我们需要用两个不同的投影矩阵将这些嵌入转换为Query和Key。
假设我们的投影矩阵是:

W_q = [
    [0.1, 0.2, 0.3],
    [0.4, 0.5, 0.6],
    [0.7, 0.8, 0.9]
]

W_k = [
    [0.9, 0.8, 0.7],
    [0.6, 0.5, 0.4],
    [0.3, 0.2, 0.1]
]

计算注意力分数
在对输入进行投影之后，会使用 Key 和 Query 向量来生成注意力分数。词之间与所有前后所有词两两组合，形成一个个词元，对每个词元进行计算注意力分数。专业点来说即是：对于序列中的每一对词元 $[i, j]$ ，我们都会计算一个注意力分数 $a [i, j]$ 。注意力分数的取值范围是 $[0, 1]$ ，它定量地表示在计算词元 $i$ 的新表示时，词元 $j$ 应该被考虑的程度。

i（当前词）	j（参与加权的词）	计算	含义
0 (“LLM”)	0 (“LLM”)	$a[0, 0] = q_0 \cdot k_0$	“LLM” 关注自己多少
	1 (“#s”)	$a[0, 1] = q_0 \cdot k_1$	“LLM” 关注 “#s” 多少
	2 (“are”)	$a[0, 2] = q_0 \cdot k_2$	“LLM” 关注 “are” 多少
	3 (“cool”)	$a[0, 3] = q_0 \cdot k_3$	“LLM” 关注 “cool” 多少
1 (“#s”)	0 (“LLM”)	$a[1, 0] = q_1 \cdot k_0$	“#s” 关注 “LLM” 多少
	1 (“#s”)	$a[1, 1] = q_1 \cdot k_1$	“#s” 关注自己多少
	2 (“are”)	$a[1, 2] = q_1 \cdot k_2$	“#s” 关注 “are” 多少
	3 (“cool”)	$a[1, 3] = q_1 \cdot k_3$	“#s” 关注 “cool” 多少
2 (“are”)	0 (“LLM”)	$a[2, 0] = q_2 \cdot k_0$	“are” 关注 “LLM” 多少
	1 (“#s”)	$a[2, 1] = q_2 \cdot k_1$	“are” 关注 “#s” 多少
	2 (“are”)	$a[2, 2] = q_2 \cdot k_2$	“are” 关注自己多少
	3 (“cool”)	$a[2, 3] = q_2 \cdot k_3$	“are” 关注 “cool” 多少
3 (“cool”)	0 (“LLM”)	$a[3, 0] = q_3 \cdot k_0$	“cool” 关注 “LLM” 多少
	1 (“#s”)	$a[3, 1] = q_3 \cdot k_1$	“cool” 关注 “#s” 多少
	2 (“are”)	$a[3, 2] = q_3 \cdot k_2$	“cool” 关注 “are” 多少
	3 (“cool”)	$a[3, 3] = q_3 \cdot k_3$	“cool” 关注自己多少

实际计算中，我们可以通过将所有的 Query 向量和 Key 向量分别堆叠成两个矩阵，并将 Query 矩阵与 Key 矩阵的转置相乘，来高效计算序列中所有词之间的注意力分数。

这个操作的结果是一个大小为 [T, T] 的矩阵（T 是序列长度），我们称其为注意力矩阵，它包含了序列中所有词对之间的注意力分数。

接着上面例子我们实例：
对于查询矩阵Q:

q_0 = embeddings[0] · W_q = [0.1, 0.2, 0.3] · W_q = [0.30, 0.72, 1.14]
q_1 = embeddings[1] · W_q = [0.4, 0.5, 0.6] · W_q = [0.66, 1.50, 2.34]
q_2 = embeddings[2] · W_q = [0.7, 0.8, 0.9] · W_q = [1.02, 2.28, 3.54]
q_3 = embeddings[3] · W_q = [1.0, 1.1, 1.2] · W_q = [1.38, 3.06, 4.74]

对于键矩阵K:

k_0 = embeddings[0] · W_k = [0.1, 0.2, 0.3] · W_k = [0.30, 0.18, 0.06]
k_1 = embeddings[1] · W_k = [0.4, 0.5, 0.6] · W_k = [0.96, 0.60, 0.24]
k_2 = embeddings[2] · W_k = [0.7, 0.8, 0.9] · W_k = [1.62, 1.02, 0.42]
k_3 = embeddings[3] · W_k = [1.0, 1.1, 1.2] · W_k = [2.28, 1.44, 0.60]

现在我们将这些向量堆叠成矩阵:

Query矩阵Q (4×3):

Q = [
    [0.30, 0.72, 1.14],  # q_0 ("LLM")
    [0.66, 1.50, 2.34],  # q_1 ("#s")
    [1.02, 2.28, 3.54],  # q_2 ("are")
    [1.38, 3.06, 4.74]   # q_3 ("cool")
]

Key矩阵K (4×3):

K = [
    [0.30, 0.18, 0.06],  # k_0 ("LLM")
    [0.96, 0.60, 0.24],  # k_1 ("#s")
    [1.62, 1.02, 0.42],  # k_2 ("are")
    [2.28, 1.44, 0.60]   # k_3 ("cool")
]

为了计算注意力分数矩阵A,我们需要Q乘以K的转置:

K的转置K^T (3×4):

K^T = [
    [0.30, 0.96, 1.62, 2.28],
    [0.18, 0.60, 1.02, 1.44],
    [0.06, 0.24, 0.42, 0.60]
]

执行矩阵乘法Q·K^T:

A = Q · K^T = [
    [0.30*0.30 + 0.72*0.18 + 1.14*0.06, 0.30*0.96 + 0.72*0.60 + 1.14*0.24, ...],
    [...],
    [...],
    [...]
]

计算完整的注意力分数矩阵:

A = [
    [0.23, 0.75, 1.27, 1.79],  # "LLM"对各词的注意力
    [0.51, 1.63, 2.76, 3.88],  # "#s"对各词的注意力
    [0.79, 2.52, 4.25, 5.98],  # "are"对各词的注意力
    [1.06, 3.40, 5.74, 8.07]   # "cool"对各词的注意力
]

这个4×4的矩阵就是注意力分数矩阵,里面的每个元素a[i,j]表示词元i对词元j的注意力分数。例如:

a[0,0] = 0.23 表示"LLM"对自己的注意力分数
a[0,1] = 0.75 表示"LLM"对"#s"的注意力分数
a[3,0] = 1.06 表示"cool"对"LLM"的注意力分数
a[3,3] = 8.07 表示"cool"对自己的注意力分数

提升训练稳定性
为了提升训练稳定性，我们将注意力矩阵中的每个值除以 √d（d 是向量维度，然后对矩阵的每一行应用 softmax 操作。

经过 softmax 后，注意力分数被归一化到 [0, 1] 之间，并构成一个有效的概率分布。
在这里插入图片描述

使用 Value 向量计算输出
一旦得到了注意力分数，计算自注意力的输出就很简单了：
每个词的输出就是对应的 Value 向量的加权平均，权重就是我们刚刚得到的注意力分数。

我们可以将所有 Value 向量堆叠成一个矩阵，然后将注意力矩阵与 Value 矩阵相乘，就可以一次性计算出整个批次的输出。

from typing import Optional, Tuple
import torch
import torch.nn as nn
from torch.nn import functional as F


class Head(nn.Module):
    """ 单头注意力机制 """

    def __init__(self, head_size: int) -> None:
        super().__init__()
        # 对输入的向量做线性变化
        self.key = nn.Linear(n_embd, head_size, bias=False)
        self.query = nn.Linear(n_embd, head_size, bias=False)
        self.value = nn.Linear(n_embd, head_size, bias=False)
        self.register_buffer('tril', torch.tril(
            torch.ones(block_size, block_size)))

        self.dropout = nn.Dropout(dropout)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        # 输入的尺寸是[B, T, d]
        # 输出的尺寸是 [B, T, hs]hs即head size是用户指定矩阵的维度，是一个超参数
        _, T, _ = x.shape
        k = self.key(x)   # (B,T,hs)
        q = self.query(x)  # (B,T,hs)
        # 计算注意力机制评分
        # (B, T, hs) @ (B, hs, T) -> (B, T, T)
        weights = q @ k.transpose(-2, -1) * k.shape[-1]**-0.5 #k.transpose(-2, -1) 是对 k 张量进行转置，交换最后两个维度。原本 k 的形状是 (B, T, D)，转置后变为 (B, D, T)
        weights = weights.masked_fill(
            self.tril[:T, :T] == 0, float('-inf'))  # (B, T, T)
        weights = F.softmax(weights, dim=-1)  # (B, T, T)
        weights = self.dropout(weights)
        # perform the weighted aggregation of the values
        v = self.value(x)  # (B,T,hs)
        out = weights @ v  # (B, T, T) @ (B, T, hs) -> (B, T, hs)
        return out

多头注意力（Multi-Head Attention）

由于相关性是多样的，比如：
Dog和Cat的相关性：都是动物
Dog和Bark的相关性：行为关系
需要多个角度捕捉不同的关联类型，从而诞生出了多头注意力。

多头注意力机制是由多个独立的注意力计算模块组成的，换句话说在代码层面多头注意力机制创建了多组QKV。

class MultiHeadAttention(nn.Module):
    """ multiple heads of self-attention in parallel """

    def __init__(self, num_heads: int, head_size: int) -> None:
        super().__init__()
        self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
        self.projection = nn.Linear(head_size * num_heads, n_embd)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        out = torch.cat([h(x) for h in self.heads], dim=-1)
        out = self.dropout(self.projection(out))
        return out

🔥 资源消耗问题

对于长度为 $n$ 的序列，注意力机制需要计算 $n^2$ 个注意力分数，这导致了计算复杂度为 $O(n^2)$ 。这种二次方增长是大型语言模型处理长序列时的主要瓶颈。

举个例子：

输入1,000个token：需要1,000² = 1,000,000次注意力计算
输入10,000个token：需要10,000² = 100,000,000次注意力计算（增加100倍！）

这就是为什么模型的上下文窗口（context window）大小成为评价LLM能力的重要指标之一。增加上下文窗口不仅需要更多的计算资源，还需要优化注意力机制来处理长序列。

4. Transformer Block结构

Transformer架构的核心是由多个相同的Transformer Block堆叠而成。这些Block在编码器(Encoder)和解码器(Decoder)中有一些关键区别。

class FeedFoward(nn.Module):
    """ a simple linear layer followed by a non-linearity """

    def __init__(self, n_embd: int) -> None:
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(n_embd, 4 * n_embd),
            nn.ReLU(),
            nn.Linear(4 * n_embd, n_embd),
            nn.Dropout(dropout),
        )

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        return self.net(x)


class Block(nn.Module):
    """ Transformer block: communication followed by computation """

    def __init__(self, n_embd: int, n_head: int) -> None:
        # n_embd: embedding dimension, n_head: the number of heads we'd like
        super().__init__()
        head_size = n_embd // n_head
        self.self_attention = MultiHeadAttention(n_head, head_size)
        self.feed_forward = FeedFoward(n_embd)
        self.layer_norm_1 = nn.LayerNorm(n_embd)
        self.layer_norm_2 = nn.LayerNorm(n_embd)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        x = x + self.self_attention(self.layer_norm_1(x))
        x = x + self.feed_forward(self.layer_norm_2(x))
        return x

class GPTLanguageModel(nn.Module):

    def __init__(self) -> None:
        super().__init__()
        # each token directly reads off the logits for the next token from a lookup table
        self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
        self.position_embedding_table = nn.Embedding(block_size, n_embd)
        self.blocks = nn.Sequential(
            *[Block(n_embd, n_head=n_head) for _ in range(n_layer)])
        self.final_layer_norm = nn.LayerNorm(n_embd)
        self.final_linear_layer = nn.Linear(n_embd, vocab_size)

        self.apply(self._init_weights)

    def _init_weights(self, module: nn.Module) -> None:
        if isinstance(module, nn.Linear):
            torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)
            if module.bias is not None:
                torch.nn.init.zeros_(module.bias)
        elif isinstance(module, nn.Embedding):
            torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)

    def forward(self, input_tokens: torch.Tensor, targets: Optional[torch.Tensor] = None) -> Tuple[torch.Tensor, Optional[torch.Tensor]]:
        """
        Forward pass of the model.

        Args:
            input_tokens: Tensor of token indices of shape (batch_size, sequence_length)
            targets: Optional tensor of target token indices of same shape as input_tokens

        Returns:
            Tuple of (logits, loss) where logits has shape (batch_size, sequence_length, vocab_size)
            and loss is optional cross-entropy loss if targets are provided
        """

        B, T = input_tokens.shape

        # input_tokens and targets are both (B,T) tensor of integers
        token_embedding = self.token_embedding_table(input_tokens)  # (B,T,C)
        positional_embedding = self.position_embedding_table(
            torch.arange(T, device=device))  # (T,C)
        x = token_embedding + positional_embedding  # (B,T,C)
        x = self.blocks(x)  # (B,T,C)
        x = self.final_layer_norm(x)  # (B,T,C)
        logits = self.final_linear_layer(x)  # (B,T,vocab_size)

        if targets is None:
            loss = None
        else:
            B, T, C = logits.shape
            logits = logits.view(B*T, C)
            targets = targets.view(B*T)
            loss = F.cross_entropy(logits, targets)

        return logits, loss

    def generate(self, input_tokens: torch.Tensor, max_new_tokens: int) -> torch.Tensor:
        """
                Generate new tokens given a context.

                Args:>ns: Starting token indices of shape (batch_size, sequence_length)
                        max_new_tokens: Number of new tokens to generate

                Returns:
                        Tensor of token indices of shape (batch_size, sequence_length + max_new_tokens)
                """

        # input_tokens is (B, T) array of indices in the current context
        for _ in range(max_new_tokens):
            # crop input_tokens to the last block_size tokens
            cropped_input = input_tokens[:, -block_size:]
            # get the predictions
            logits, _ = self(cropped_input)
            # focus only on the last time step
            logits = logits[:, -1, :]  # becomes (B, C)
            # apply softmax to get probabilities
            probs = F.softmax(logits, dim=-1)  # (B, C)
            # sample from the distribution
            idx_next = torch.multinomial(probs, num_samples=1)  # (B, 1)
            # append sampled index to the running sequence
            input_tokens = torch.cat(
                (input_tokens, idx_next), dim=1)  # (B, T+1)
        return input_tokens

编码器(Encoder)块结构

编码器块包含以下核心组件：

多头自注意力(Multi-Head Self-Attention)

功能：允许模型同时关注序列不同位置的信息，从不同的表示子空间捕获不同类型的关系
计算过程：
1. 将输入分成h个头(heads)
2. 每个头独立计算注意力
3. 拼接所有头的输出
4. 通过线性投影整合结果
特点：由于每个头可以学习不同的注意力模式，多头机制增强了模型的表达能力

残差连接(Residual Connection)

功能：缓解深层网络训练中的梯度消失问题
实现：将子层的输入直接添加到其输出
优势：使信息能够直接在层间传递，帮助维持梯度流动

层归一化(Layer Normalization)

功能：稳定深层网络的训练过程，加速收敛
计算：归一化每个样本的特征，使其均值为0，方差为1，然后应用缩放和偏移
位置：在Transformer中，层归一化通常应用在每个子层的输出和残差连接之后

前馈神经网络(Feed-Forward Network)

功能：对注意力机制捕获的上下文信息进行非线性转换
结构：两层全连接网络，中间有ReLU激活函数
维度：通常中间层维度比输入/输出维度大几倍(例如4倍)，增强模型表达能力

完整的编码器块
编码器块的完整前向传播过程：

输入经过多头自注意力层
应用残差连接和层归一化
结果通过前馈网络
再次应用残差连接和层归一化

解码器(Decoder)块结构

解码器块包含编码器块的所有组件，但有以下关键区别和额外组件：

掩码自注意力(Masked Self-Attention)

功能：防止当前位置关注未来位置的信息，确保自回归生成
实现：在计算注意力分数时，将未来位置的分数设置为负无穷大（通过掩码矩阵实现）
目的：解码时每个位置只能关注当前及之前的位置，符合从左到右生成文本的过程

编码器-解码器注意力(Encoder-Decoder Attention)

功能：允许解码器关注编码器的全部输出序列
特点：
1. Query来自解码器前一层输出
2. Key和Value来自编码器的最终输出
3. 这种跨注意力机制使解码器能利用编码器处理的源序列信息

编码器和解码器的主要区别

特性	编码器(Encoder)	解码器(Decoder)
注意力类型	标准自注意力	掩码自注意力 + 编码器-解码器注意力
信息获取	双向上下文(可关注序列任何位置)	单向上下文(只能关注当前及之前位置)
主要用途	理解和编码输入序列	生成输出序列
并行性	可全并行计算	生成时只能自左向右顺序计算
块数量	通常为6个(基本Transformer)	通常为6个(基本Transformer)

编码器-解码器架构与仅…的比较

原本Transformer就是用来做翻译的，因此编码器-解码器结构也通常是翻译相关的

架构类型	代表模型	适用任务	工作流程	注意力机制
编码器-解码器架构	Transformer BART T5 mT5	机器翻译文本摘要问答对话系统	1. 编码器处理完整输入序列 2. 解码器利用编码器输出生成目标序列	编码器：双向自注意力解码器：掩码自注意力+编码器-解码器注意力
仅解码器架构	GPT系列 LLaMA Claude Falcon	文本生成对话续写完形填空	1. 使用掩码自注意力处理上下文 2. 自回归地预测下一个词元	掩码自注意力（单向，只关注当前及之前位置）
仅编码器架构	BERT RoBERTa DeBERTa XLM-R	分类命名实体识别情感分析文本匹配	1. 双向处理输入序列 2. 生成上下文化表示用于下游任务	双向自注意力（可关注序列中任意位置）