k-means

一、概念介绍

1.1、相似性与据类分析

  人类认识世界，接受信息有超过80%都是源于视觉图像，比如形状、颜色等。人类对于他们的识别都是基于事物间的相似性的，所以研究相似性尤其有价值。

   聚类就是要挖掘数据的蕴含的相似性的结构信息。这里相似性是人为主观定义的。

1.2、聚类分析原理

1.2.1、有16张扑克牌，如何将他们分组呢？

无论选择哪种划分方法，关键在于我们怎样定义并度量“相似性”

1.2.2、相似是主观的, 是否是一类

1.3、相似度计算方法

  估算不同样本之间的相似性(Similarity Measurement)通常采用的方法就是计算样本间的“距离”(Distance)，相似性度量方法有：欧氏距离、余弦夹角、杰卡德相似系数、马氏距离、信息熵等

1.4、数据集的划分

左图有一些数据点，可以划分为3个簇，对应于右图，不同的分组显示不同的颜色。

怎么教计算机按照人的思维去做同样的事情呢？

1.5、性能评价指标

E越小，表示数据点越接近它们的中心，聚类效果越好。误差取了平方，表明更加重视那些远离中心的点。

二、k-means

前面的式子无法用解析的方式求最小，常采用迭代收敛方式。

2.1、K-means算法

输入：含n个样本的数据集，簇数K
输出：k个簇
算法步骤：

• 1.初始化k个初始聚类中心 (通常随机选择);
• 2.将每个样本$x_i(i=1,...n)$分配到与之最近的中心所在的簇;
• 3.更新聚类中心（各个簇的样本均值);
• 4.重复2,3直到每个样本点划分结果都不再发生改变

2.2、K-means算法过程示意图

2.3、K-means算法实例

2.3.1、选择初始聚类中心，计算各个样本到中心距离

2.3.2、更新聚类中心

通过划分后的簇 获取平均值， 作为新的中心

2.4、代码实现

2.4.1、伪代码

2.4.2、代码

2.4.2.1、加载数据

#读数据
#将testSet.txt文本文件中的数据存储到dataMat。它包含许多列表的列表，这种格式方便将很多值封装到矩阵中。
def loadDataSet(fileName):        
    dataMat = []                            #创建列表，存储读取的数据
    fr = open(fileName)
    for line in fr.readlines():             #读每一行
        line1=line.strip();                 #删头尾空白
        curLine = line1.split('\t')         #以\t为分割，返回一个list列表
        # python3.x中map的返回类型是 ‘map’类，它返回的是该对象的内存地址，不能进行计算，需要将map转换为list
        fltLine = list(map(float,curLine))        #str 转成  float
        print(fltLine)
        dataMat.append(fltLine)             #将元素添加到列表尾
    return dataMat

2.4.2.2、初始化聚类中心

可以随机从数据集中选取k个样本作为初始化聚类中心，而这里采用随机生成边界范围内的值的方法。
随机生成的质心必须要在数据集的范围内，这可以根据找每一维的最小值与最大值来完成，在最小值与最大值的范围内，通过随机产生0-1之间的随机数，确保随机点在数据的边界范围内。

#初始化聚类中心
def randCent(dataSet, k):
    n = shape(dataSet)[1]                   #特征维度
    # 创建 k x n 的零矩阵
    centroids = mat(zeros((k,n)))           #创建聚类中心的矩阵 k x n
    for j in range(n):                      #遍历n维特征
        minJ = min(dataSet[:,j])            #第j维特征属性值min   ,1x1矩阵
        rangeJ = float(max(dataSet[:,j]) - minJ)    #区间值max-min，float数值
        centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1))#第j维，每次随机生成k个中心
    return centroids

初始化聚类中心的方法，也可以从测试数据集中，随机抽取k个样本作为初始化的聚类中心。

2.4.2.3、计算距离

k-means算法迭代过程，需要计算距离，常用的计算距离是欧氏距离，也可以使用其他距离函数。

#算距离
def distEclud(vecA, vecB):                  #两个向量间欧式距离
    return sqrt(sum(power(vecA - vecB, 2))) #la.norm(vecA-vecB)

2.4.2.4、kMeans() 函数

#k-means算法  （#默认欧式距离，初始中心点方法randCent（））  
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent): 
    m = shape(dataSet)[0]   #m个样本
    clusterAssment = mat(zeros((m,2)))  #分配样本到最近的簇：存[簇序号,距离的平方] 
     
        #step1:#初始化聚类中心                                     
    centroids = createCent(dataSet, k)   
    
    clusterChanged = True
    while clusterChanged:   #所有样本分配结果不再改变，迭代终止
        clusterChanged = False
        
        #step2:分配到最近的聚类中心对应的簇中
        for i in range(m):   
            minDist = inf; minIndex = -1  #对于每个样本，定义最小距离
            for j in range(k):  #计算每个样本与k个中心点距离
                distJI = distMeas(centroids[j,:],dataSet[i,:]) 
                if distJI < minDist: 
                    minDist = distJI; minIndex = j  #获取最小距离,及对应的簇序号
            if clusterAssment[i,0] != minIndex: clusterChanged = True 
            clusterAssment[i,:] = minIndex,minDist**2 #分配样本到最近的簇
        print(centroids)
        
        #step3:更新聚类中心
        for cent in range(k):#样本分配结束后，重新计算聚类中心
            #获取该簇所有的样本点
            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]
            #更新聚类中心：axis=0沿列方向求均值
            centroids[cent,:] = mean(ptsInClust, axis=0) 
    return centroids, clusterAssment

2.4.2.5、 测试

#-*- coding: utf-8 -*- 
from numpy import*
from matplotlib import pyplot as plt

#step1:读取数据并解析为所需格式
from src.main.python.test.kmeans import kMeans

# 数据集
datamat=mat(kMeans.loadDataSet('testSet.txt'))


#step2:聚类
k=4    #用户定义聚类数
for i in range(1):
    mycentroids,clusterAssment=kMeans.kMeans(datamat,k)
    #step3:绘图显示
    kMeans.datashow(datamat,k,mycentroids,clusterAssment)

三、K-means的优缺点

3.1、优点

比较简单，容易实现；
处理大数据集时，保持可伸缩性和高效性；
当结果簇是密集的，聚类效果较好。

3.2、缺点

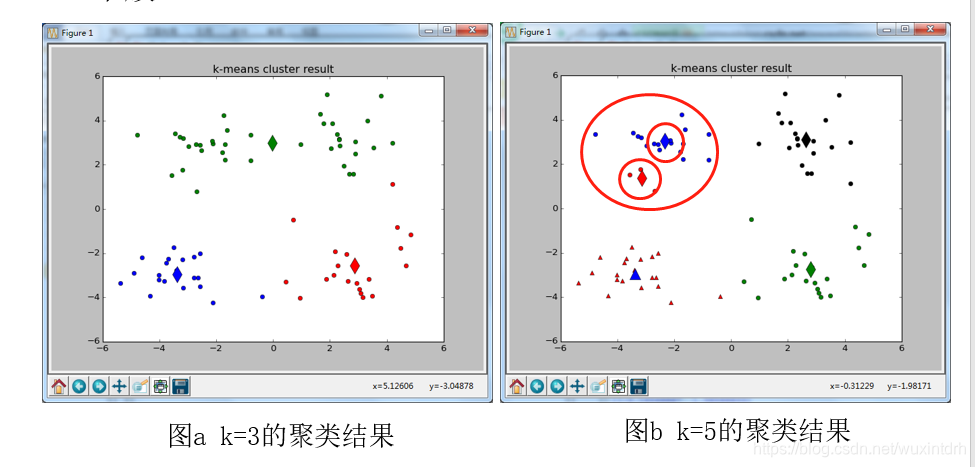
3.2.1、k由用户给定，不同的k对聚类结果影响很大

如下分别为k=3和k=5的聚类结果。当k=3时，绿色的簇可以划分为两个；当k=5时，红色圆和蓝色圆两个簇应该合并成一个簇。

5.2.2、对初始化聚类中心的选择敏感；

不同的初始聚类中心，会得到不同的聚类结果，容易陷入局部最优值。如下图，k=4时，结果收敛了，但是陷入局部最小值。

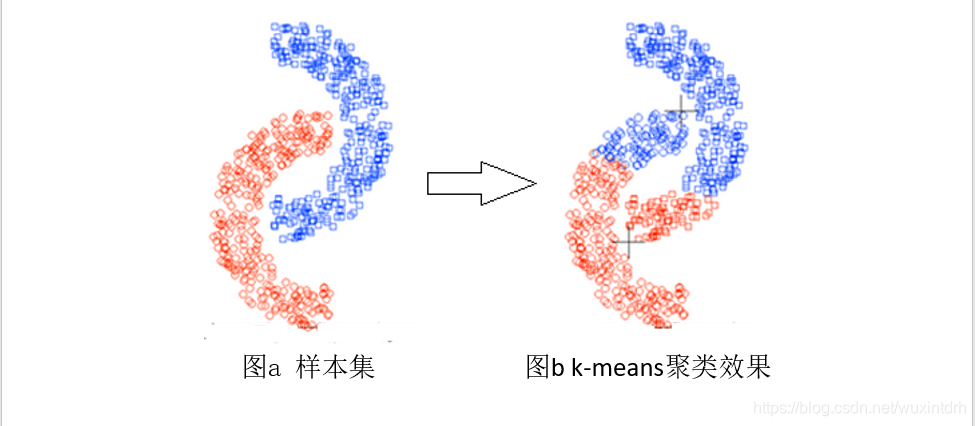
3.2.3、不适合于发现非凸面形状的簇或者大小差别很大的簇；

不同的初始聚类中心，会得到不同的聚类结果，容易陷入局部最优值。如下图，k=4时，结果收敛了，但是陷入局部最小值。

3.2.4、对躁声和孤立点数据敏感

四、K-means的改进