2.2.6 树

最新推荐文章于 2024-07-20 16:10:44 发布

有时教辅

最新推荐文章于 2024-07-20 16:10:44 发布

阅读量147

点赞数 3

分类专栏：计算机等级考试二级公共基础文章标签： c语言数据结构

本文链接：https://blog.csdn.net/x000123/article/details/134063460

版权

计算机等级考试同时被 2 个专栏收录

12 篇文章 0 订阅

订阅专栏

二级公共基础

12 篇文章 1 订阅

订阅专栏

1、树的基本概念

树结构是一种重要的非线性结构，它主要用来表示层次结构的，即数据元素之间存在1对多的关系。日常生活中比较常见的一种树形结构，就是组织机构的树形表示。比如高校的组织结构图：

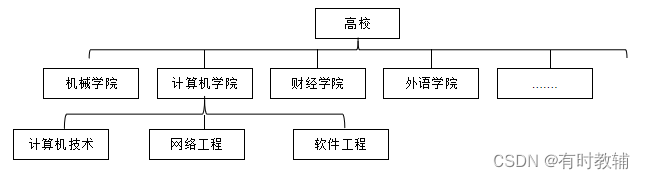
图2.2.19高校组织结构图

从上图中可以看出，所有数据元素中，有且仅有一个数据元素没有直接前驱，比如上图中的‘高校’。而其他剩余数据元素有且仅有一个直接前驱，但所有数据元素的直接后驱则可以是0个、1个或多个。

基于此，我们可以这样定义树结构：

假设树是n个结点的有限集合。当它是一个非空树时，满足以下条件：

有且仅有一个根结点；
当结点数量大于1时，其余结点可以分为若干个相关独立的有限集，而每个集合本身也是一颗树，被称为根的子树。

上面所说的树定义是一个递归定义，不太容易理解。关于树，我们可以简单的理解为：

对于有n个结点的树而言，其仅有一个根节点，除根结点外的其他节点，有且仅有一个父结点。树结构中的一些基本概念列示如下：

树的结点	类似线性表中的结点概念，即包含数据域（存储数据元素），同时又包含若干个指向其子树结点地址的指针域。
根结点	在树型结构中，有且仅有一个结点没有直接前驱，但可以有0个、1个或多个直接后驱，该结点就称为根结点。如下图2.2.16中A结点。
父结点	如果一个结点有直接前驱，则直接前驱就称为该结点的父结点；注意根节点也是一个父结点，但父结点不一定是根结点，有些父结点也是有直接前驱的，即它还有自己的父结点。如下图2.2.16中的A、B、C、D、E、F都是父结点，但只有A是根结点。
子结点	如果一个结点既有直接前驱，又有直接后驱，则称为子结点。如下图2.2.16中B、C、D、E、F结点。
叶结点	如果一个结点只有直接前驱，但没有直接后驱，则称为叶结点；叶结点也可以看成是没有直接后驱的子结点。如下图2.2.16中G、H、I、J、K、L结点。
子树	以某结点的一个子结点作为根结点形成的树，可以称为该结点的子树。如下图2.2.17就是图2.2.16中A结点的子树。
结点的度	某结点的直接后驱个数，称为该结点的度。如下图2.2.16中A结点的度为3；B结点的度为2。
树的度	一棵树中，所有结点的最大的度，称为该树的度。如下图2.2.16中结点度最大的是3（A结点的度），所以树的度也为3。
深度/高度	一棵树中，根节点在第一层次，其直接后驱在第二层次，依次类推，若一个结点在第n层次，其直接后驱在n+1层次，我们把树中结点的最大层次称为树的深度或高度。如下图2.2.16中结点A在第一层，结点B、C、D在第二层，结点E、F、G、H、I在第三层，结点JKL在第四层，最大层次是4,所以这课树的高度为4。
森林	M棵互不交互的树所组成的集合，称为森林。如下图2.2.18所示，是由三棵树组成的森林。

表2.2.2

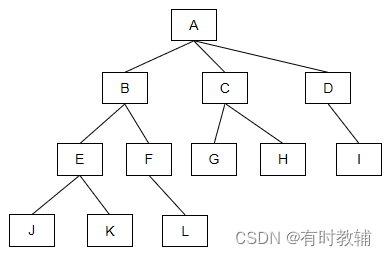
图2.2.20树的示例

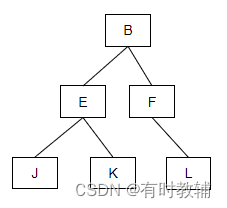
图2.2.21子树的示例

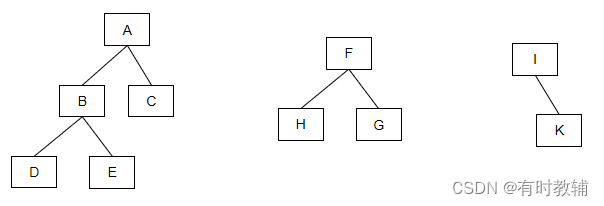
图2.2.22森林的示例

2、二叉树的定义及其存储

(1)二叉树的定义

二叉树是一种特殊的树形结构，其主要特点是每个结点最多有两个子树（或两个直接后驱），且子树有左右之分，其次序不能改变。在根结点右下面的称为右子树，左下面的称为左子树。如下图所示：

图2.2.23二叉树

由上图可知，B是A的左子树，C是A的右子树；D是B的左子树，但B没有右子树；

(2)二叉树的性质

二叉树具有如下表列示的特性：

性质	举例阐述
在二叉树的第i层上至多有2i-1个结点	这是因为每个结点最多有两个直接后驱
深度k的二叉树至多有2k-1个结点	根据性质1，可以得出第i层的最大结点数为2i-1，则深度为k的二叉树，其最多的结点个数应该为所有层次的最大结点数之和，即=
对任何一个二叉树而言，度为0的结点数总比度为2的结点数多一个。
具有n个结点的二叉树，其深度至少为[log2n]+1，其中[ ]表示对里面的内容取整数部分。	比如[3.56]的含义就是取3.56的整数部分，即[3.56]=3

表2.2.3

(3)二叉树的特殊形态

二叉树存在特殊的形态，主要是满二叉树和完全二叉树，描述如下：

满二叉树，其特点就是二叉树的每一层的结点数都是该层的最大结点数。即如果一颗二叉树深度为k，则其有2k-1个结点。通俗的讲，就是除最后一层结点的子树数为0外，其他层次结点的子树数都是2，如下图所示：

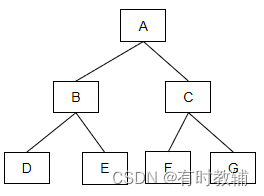
图2.2.24满二叉树

完全二叉树，其特点是除最后一层外，其他层的结点数都是该层的最大结点数，而在最后一层上，其结点从左到右排列，中间不允许有空，如下图所示：

图2.2.25完全二叉树

从以上定义来看，满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树。

(4)二叉树的存储

二叉树的存储结构也分为顺序存储和链式存储。

顺序存储，就是用一组连续的地址空间依次从上而下，从左至右的存储二叉树上的结点元素。举例如下:

图2.2.26 二叉树的顺序存储

顺序存储一般只适用于完全二叉树，因为对于一般的二叉树来说，存在空间浪费的情况，如果该二叉树是一个所有结点都只有一个子树的情况下，则浪费的空间更为严重，即只有k个结点，却需要2k-1个存储空间。存储空间浪费的情况举例如下：

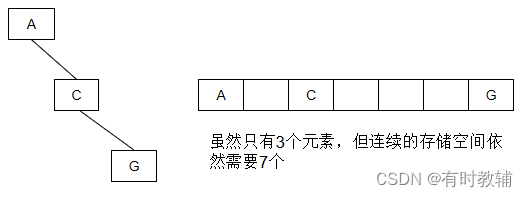
图2.2.27 顺序存储浪费空间示例

链式存储，就是用含有一个数据域和两个指针域的存储结点来表示一个树结点，其中两个指针域分别指向该结点的左右子结点。存储结点结构如下图所示：

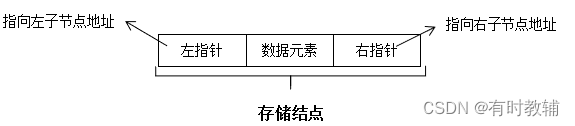
图2.2.28 存储结点结构

链式存储举例如下：

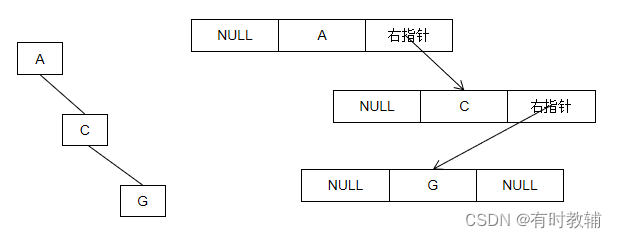
图2.2.29 链式存储示例

从图2.2.25可知，即便是比较特殊的二叉树，链式存储也不存在空间浪费的情况，有几个数据元素，就只需要几个存储结点。

3、二叉树的遍历

二叉树的遍历是指按某条访问路径，可以顺序访问树中的每一个结点，且使得每个结点只被访问一次。按根结点在访问顺序上的不同，可以将二叉树的遍历分为三种，先序遍历、中序遍历和后序遍历。

(1)先序遍历

也称先根遍历，其访问的过程如下：

<1>访问根结点

<2>访问子左树，访问子左树时，采用的是先序遍历方法

<3>访问子右树，访问子右树时，采用的是先序遍历方法。

以上定义是一个递归的定义，简单的说，就是先访问根结点，在访问子左树和子右树。而对每一个子树，也是先访问子树的根结点，在访问子树的子左树和子右树，依次类推，直到访问完所有的结点。举例阐述如下：

图2.2.30 二叉树示例

如上图2.2.30所示的二叉树，其先序遍历的思路如下：

先根节点，所以第一个访问的是结点A，然后访问A的左子树，如下图所示：

图2.2.31 结点A的左子树

在访问结点A的左子树时，继续使用先序访问，如上图所示，先访问左子树的根结点，即结点B。然后在访问结点B的左子树，如下图所示：

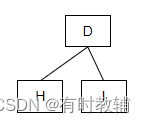
图2.2.32 结点B的左子树

在访问结点B的左子树时，继续使用先序访问，如上图所示，先访问左子树的根结点，即结点D。然后在访问结点D的左子树。
在访问结点D的左子树时，由于结点D的左子树是一个叶子结点H，其没有左右子树，所以直接访问结点H。
结点D的左子树访问完毕后，再访问结点D的右子树，由于结点D的右子树也是一个叶子结点I，其没有左右子树，所以也是直接访问结点I。
此时B结点的左子树已经访问完毕，应该访问B结点的右子树了，如下图所示：

图2.2.33 结点B的右子树

在访问B结点的右子树时，依然采用先序访问，如上图所示，先访问右子树的根结点，即结点E。然后在访问结点E的左子树。
在访问结点E的左子树时，由于结点E的左子树是一个叶子结点J，其没有左右子树，所以直接访问结点J。
此时结点A的左子树已经访问完毕，应该访问A结点的右子树了，如下图所示：

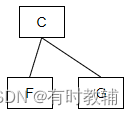
图2.2.34 结点A的右子树

再访问结点A的右子树时，依然采用先序访问，如上图所示，先访问右子树的根结点，即结点C。然后在访问结点C的左子树。
在访问结点C的左子树时，由于结点C的左子树是一个叶子结点F，其没有左右子树，所以直接访问结点F。
结点C的左子树访问完毕后，再访问结点C的右子树，由于结点C的右子树也是一个叶子结点G，其没有左右子树，所以也是直接访问结点G。
此时，结点A的右子树也访问完毕。整棵二叉树的结点均被访问到，其依次访问的结点顺序是A、B、D、H、I、E、J、C、F、G。

(2)中序遍历

也称中根遍历，其访问的过程如下：

<1>访问子左树，访问子左树时，采用的是中序遍历方法

<2>访问根结点。

<3>访问子右树，访问子右树时，采用的是中序遍历方法

简单的说，就是先子左树，在访问根结点，之后访问子右树。在访问子左树和子右树的时候，也是按照先访问子树的子左树，在访问子树的根结点，最后访问子树的子右树。依次类推，直到访问完所有的子树。举例阐述如下：

我们依然用图2.2.30的二叉树为例，其中序遍历思路如下：

先访问左子树，而根结点A的左子树如图2.2.31所示。
在访问根结点A的左子树时，依然采用中序访问，所以需要先访问图2.2.31二叉树的左子树，即结点B的左子树，如图2.2.32所示。
在访问结点B的左子树时，依然采用中序访问，所以需要先访问图2.2.32二叉树的左子树，即结点D的左子树。
在访问结点D的左子树时，由于结点D的左子树是一个叶子结点H，其没有左右子树，所以直接访问结点H。
访问完结点D的左子树后，则根据中序访问规则，紧接着需要访问的是根结点，即结点D。然后需要访问结点D的右子树。
在访问结点D的右子树时，由于结点D的右子树是一个叶子结点I，其没有左右子树，所以直接访问结点I。
此时图2.2.32的二叉树访问完毕，也即结点B的左子树访问完毕。根据中序访问规则，紧接着需要访问根结点，即结点B。然后需要访问结点B的右子树，如图2.2.33所示。
在访问结点B的右子树，依然采用中序访问，所以需要先访问图2.2.33二叉树的左子树，即结点E的左子树。
在访问结点E的左子树时，由于结点E的左子树是一个叶子结点J，其没有左右子树，所以直接访问结点J。
访问完结点E的左子树后，则根据中序访问规则，紧接着需要访问的是根结点，即结点E。然后需要访问结点E的右子树。而由于结点E没有右子树，则无需访问。此时图2.2.33的二叉树访问完毕，即结点B的右子树访问完毕。继而图2.2.31的二叉树也访问完毕，即结点A的左子树访问完毕。
A结点的左子树访问完毕后，则根据中序访问规则，紧接着需要访问的是根结点，即结点A。然后需要访问结点A的右子树，即图2.2.34的二叉树。
在访问结点A的右子树时，依然采用中序访问，所以需要先访问图2.2.34二叉树的左子树，即结点C的左子树。
在访问结点C的左子树时，由于结点C的左子树是一个叶子结点F，其没有左右子树，所以直接访问结点F。
结点C的左子树访问完毕后，根据中序访问规则，紧接着需要访问的是根结点，即结点C。然后需要访问结点C的右子树。
在访问结点C的右子树时，由于结点C的右子树是一个叶子结点G，其没有左右子树，所以直接访问结点G。
此时，结点A的右子树也访问完毕。图2.2.30所示的二叉树的结点均被访问到，其依次访问的结点顺序是H、D、I、B、J、E、A、F、G。