动手学深度学习——求导

1. 导数与微分

导数描述了函数在某一点处的瞬时变化率，即函数在该点处切线的斜率。

微分则是函数在某一点处的局部线性逼近，可以看作是导数的一个近似。如果一个函数f(x)在每个点a处存在导数，我们就称f(x)在a处是可微的。

用途：

• 在神经网络训练中，要让模型变得更好则意味着最小化一个损失函数（loss function）。
• 我们通常会选择对于模型参数可微的损失函数，这样就能通过导数来确定函数的局部极值点。
• 如果沿着导数的负方向更新参数，就能减小损失函数的值。

2. 求导规则

2.1 常见函数求导

如果用D表示微分，则可以使用以下规则来对常见函数求导：

2.2 组合函数求导

对于一些由常见函数组成的函数，则有以下规则：
1）函数与常数相乘求导：

2）函数相加求导：

3）函数相乘求导：

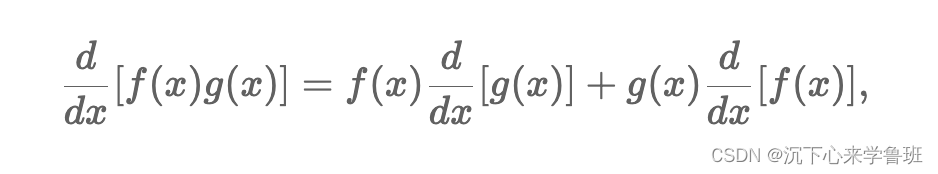
4）函数相除求导：

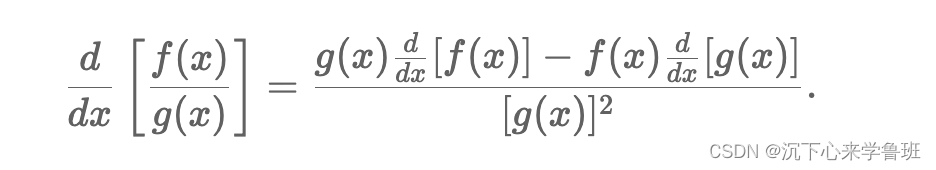
2.3 亚导数

上面都是对于可微的函数，要想对不可微的函数例如y=|x|求导，可以采用亚导数，D|x|有以下三种情况：

• 1， if x > 0
• -1， if x < 0
• a， if x = 0, -1 < a < 1

3. 梯度

将导数由标量拓展到向量后，就称为梯度，梯度一定指向值变化最大的方向。

向量求导要特别注意形状的变化。

• 标量对标量求导，结果仍然是一个标量。
• 标量y对列向量x求导，是将y对向量x中每一个元素分别求导，结果是一个行向量。
• 向量对标量求导，结果是一个列向量。
• 向量y对向量x求导，等价于y中每个元素（标量）分别对向量x求导，得到多个行向量，就组成一个矩阵。
• 矩阵（m,l)对向量(n,)求导，会得到一个（m,l,n)的三维矩阵。
• 矩阵（m,l)对矩阵（n,k)求导，会得到一个（m,l, k, n)的二维矩阵。

梯度计算的目的是寻找变化最大的点。

用途：优化模型的参数，通过梯度可以确定参数的更新方向和大小，使得模型逐渐优化，损失函数逐渐减小。

4. 链式法则

定义：复合函数的导数等于外层函数对内层函数的导数乘以内层函数对自变量的导数。

链式法则主要用于对深度学习中的是复合多元函数进行求导，假设y=f(u), u=g(x)，则y对x的求导为：

链式法则求导示例：

5. 自动求导

5.1 计算图

自动求导是通过计算图做出来的，计算图基本和链式法则的求导过程原理相似：

• 先将计算过程分解成一步步公式，得到一个无环的计算图
• 将整个求导分解成每一步公式分别求导
• 最终得出整个求导公式
  

计算图分为显式构造和隐式构造：

• 显式构造：MxNet, tensorflow
• 隐式构造：pytorch

5.2 自动求导的两种模式

求导的目的是为了寻找参数更新的方向和大小，自动求导有两种方式：

• 正向累积
• 反向累积

正向传播(又称前向传播)，从输入层开始，每一层计算的输出结果作为下一层的输入，继续向前传播，最终得到整个神经网络的输出结果（图中从a->b->z)。

在前向传播过程中，每一层的神经元接收上一层的输出，并根据权重和偏置进行加权求和，并经过激活函数进行非线性变换，得到该层的输出结果。

反向累积：

• 在前向传播时，存储中间计算结果（上图中的a和b的计算结果）。
• 沿着图反向传播时，将前面存储的中间结果拿过来用，减少计算量。
• 存储正向的所有中间结果，也是深度神经网络训练时非常耗GPU资源的原因。

正向累积和反向累积的对比：

• 计算复杂度：正向与反向相差不大，都是O(n), n是操作算子个数。
• 内存复杂度：正向复杂度为O(1)，而反向复杂度为O(n), 因为它保存了所有层的中间计算结果。

正向累积的问题在于：每层计算都要扫一遍前向传播的过程。

原因：梯度是通过链式法则逐层传播得到的，为了计算某一层的梯度，需要先计算该层之前的所有层的输出结果，也就是需要重复进行前向传播过程。

5.3 反向传播进一步理解

在神经网络训练过程中，会先走前向传播，再走反向传播。

• 前向传播用于预测，针对一个输入数据计算得到神经网络的预测结果。
• 反向传播用于更新模型参数，从输出层开始，根据损失函数来计算梯度，然后逐层向前传播梯度，利用链式法则计算每一层的梯度，这个梯度可以用来更新和优化该层的模型参数。

通过计算损失函数对模型参数的梯度，可以确定参数的更新方向和大小，从而使模型向损失函数的最小值方向调整。

保存前向传播的中间结果，具体是指：

• 激活函数的输入，会用于计算梯度。
• 权重和偏置：在前向传播过程中会被使用，同时也需要在反向传播时更新。
• 池化层和批归一化层的输出，这些也会用于计算梯度

这些变量或值在前向传播过程中会被计算，保存为中间结果后，也能用于反向传播的梯度计算和更新参数。

5.4 自动求导示例

假设x是一个列向量，y=2*x*x

import torch

# 等价x=torch.arange(4.0,requires_grad=True)
x = torch.arange(4.0)   # tensor([0., 1., 2., 3.])
x.requires_grad_(True)  # 找一个地方来保存向量x的梯度值
x.grad                  # 梯度值初始是None

计算y：

y = 2 * torch.dot(x, x)
y
> tensor(28., grad_fn=<MulBackward0>)

对y调用反向传播函数来计算x向量每个分量（元素）的梯度：

y.backward()    # 反向传播计算梯度
x.grad          # 输出向量x的梯度

> tensor([ 0.,  4.,  8., 12.])

这与我们手动求导得出的结果一致(y=2*x*x 对于x的梯度 =4x)。