一.什么是熵
Ⅰ.信息量
首先考虑一个离散的随机变量x,当我们观察到这个变量的一个具体值的时候,我们接收到多少信息呢?
我们暂时把信息看做在学习x的值时候的”惊讶程度”(这样非常便于理解且有意义).当我们知道一件必然会发生的事情发生了,比如往下掉的苹果.我们并不惊讶,因为反正这件事情会发生,因此可以认为我们没有接收到信息.但是要是一件平时觉得不可能发生的事情发生了,那么我们接收到的信息要大得多.因此,我们对于信息内容的度量就将依赖于概率分布p(x).
因此,我们想要寻找一个函数h(x)来表示信息的多少且是关于概率分布的单调函数.我们定义:
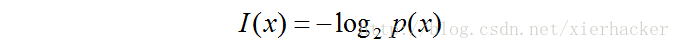
我们把这个公式叫做信息量的公式,前面的负号确保了信息一定是正数或者是0.(低概率事件带来高的信息量).
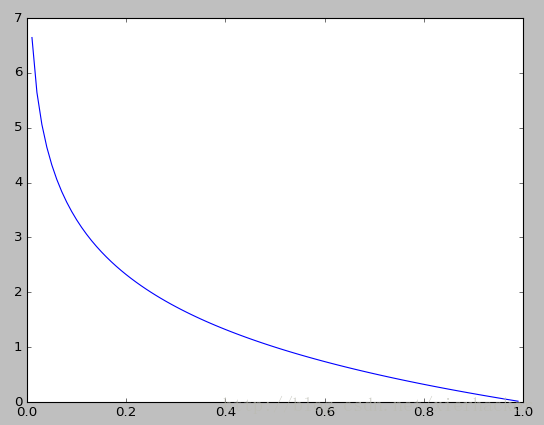
函数如下图所示
补充:上面是以2为对数的底,实际上,这个底是能够是其他的数字的.常用的是2和e这两个底.底是2的时候,单位为bit..底是e的时候,单位为nat.
有时候有人也叫做自信息(self-information),一个意思啦。可以推广一下下。
联合自信息量:
条件自信息量:
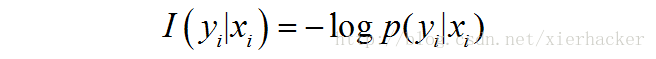
通俗一点来说的话,就是概率论中很简单的推广就行了。有概率基础的话,这个很容易理解。这里因为实际上面使用二维的更多一点就以二维为例子,推广到多维的话也是可以的。
Ⅱ.熵
熵(entropy):上面的Ⅰ(x)是指在某个概率分布之下,某个概率值对应的信息量的公式.那么我们要知道这整个概率分布对应的信息量的平均值.这个平均值就叫做随机变








 这篇博客详细介绍了信息熵的相关概念,包括信息量、熵、相对熵和互信息。熵作为衡量随机变量不确定性的指标,从离散随机变量的熵到条件熵,再到联合熵和复合熵的讨论,深入浅出地阐述了熵的各种形式和计算。相对熵(KL散度)用于度量两个概率分布的相似性,而互信息则表示一个随机变量对另一个随机变量的不确定性减少程度。文章通过实例和公式推导帮助读者理解这些概念。
这篇博客详细介绍了信息熵的相关概念,包括信息量、熵、相对熵和互信息。熵作为衡量随机变量不确定性的指标,从离散随机变量的熵到条件熵,再到联合熵和复合熵的讨论,深入浅出地阐述了熵的各种形式和计算。相对熵(KL散度)用于度量两个概率分布的相似性,而互信息则表示一个随机变量对另一个随机变量的不确定性减少程度。文章通过实例和公式推导帮助读者理解这些概念。
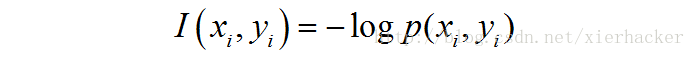
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 16万+
16万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








