FZU 1759 欧拉降幂

http://acm.fzu.edu.cn/problem.php?pid=1759

Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).

Input

There are multiply testcases. Each testcase, there is one line contains three integers A, B and C, separated by a single space.

 

Output

For each testcase, output an integer, denotes the result of A^B mod C.

 

Sample Input

3 2 4
2 10 1000

Sample Output

1
24

题目大意：计算A^B%C。

思路：A、C数据范围允许我们用long long来读，但是B的范围太大了，应该用字符数组来存储。

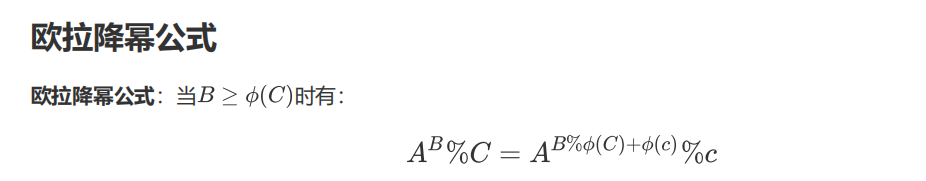
这是广义降幂公式，不要求A与C互质！当B<φ(C)时，就没有降幂的必要了。(感觉这道题数据好弱？最开始的代码没有区分这一点但是还是AC了)

然后降幂就好了~公式中的φ(C)是欧拉函数，不知道的可以看一下这篇题解：

https://blog.csdn.net/xiji333/article/details/86694357

也可以看百度百科的介绍：

https://baike.baidu.com/item/欧拉函数/1944850?fr=aladdin

然后对照一下代码里面求欧拉函数的函数的写法应该就懂了。

哦对，还需要用到快速幂，其实利用的就是二进制。不懂的可以照着过程自己模拟一下，举个例子：

要计算3^10，一般的算法要迭代10次，我们看快速幂的做法，10可以表示成：8+2，那么3^10=3^8 * 3^2，10的二进制形式是00010100，那么只要在第3位和第5位做两次乘法运算就可以了。反正就是这么个思想，效率是O(lgn)级别的，比一般的迭代快多了，具体的看代码。

还是解释一下降幂的过程，因为幂B是一个高精度数，我们不妨设其个位、十位……分别为：a0,a1,a2,……an；那么B=a0+a1*10+……+an*(10^n)，那么B%c=a0%c+a1*10%c+……+an*(10^n)%c。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;

ll phi(ll n)       //直接法求欧拉函数值
{
	ll ret=n;
	ll i;
	for(i=2;i*i<=n;i++)
        {
		if(n%i==0)
                {
                    ret-=ret/i;
			while(n%i==0)
                            n/=i;
                }
	}
	if(n>1)
            ret-=ret/n;
	return ret;
}

ll qpow(ll a, ll b, ll c)  //快速幂
{
	ll res=1;
	while(b)
        {
		if(b&1)
                    res=res*a%c;
		a=a*a%c;
		b>>=1;
	}
	return res;
}

int main()
{
	ll a, c;
	char b[1000010];
	while(~scanf("%I64d %s %I64d",&a,b,&c))
        {
		ll phic=phi(c);
		int i,len=strlen(b);
		ll res=0;
		int flag=1;
		for(i=0;i<len;i++)
                {
			res=res*10+b[i]-'0';
			if(res>=phic)
                        {
                            flag=1;
                            res%=phic;
                        }
		}
		if(flag)
                    res+=phic;
                printf("%I64d\n",qpow(a,res,c));
	}
	return 0;
}

提供φ(n)的另外一种计算方法：

int euler(int n)
{
    int ret=1,i;
    for(i=2;i*i<=n;i++)
    {
        if(n%i==0)  //满足条件的i一定为质数
        {
            n/=i,ret*=i-1;  //i为质数时 φ(i)=i-1
            while(n%i==0) n/=i,ret*=i; //n为质数i的k次幂 φ(n)=(i-1)*(i^(k-1))
        }                              //上面ret已经乘过i-1 且n已经除过i
    }
    if(n>1) ret*=n-1;
    return ret;
}