概率论基础__排列与组合

在古典概型中， 计算事件的概率经常用到排列组合及其总数计算公式， 在此给出排列组合的定义及其相关公式。

一. 两个基本原理

1. 乘法原理

如果某件事需经 k 步才以完成， 做第一步有 m₁种方法， 做第二步有 m₂ 种方法，... 做第 k 步有 种方法， 那么完成这件事共有 种方法。

2. 加法原理

如果某件事可由 k 类  不同途径之一去完成， 在第一类途径中有 m₁ 种完成方法， 在第二类途径中 有 m₂ 种完成方法, ... 在第 k 类途径中有 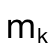种完成方法， 那么完成这件事共有   种方法。

排列和组合的公式都基于以上两个基本原理。

二. 排列

   1. 定义  

当 r = n时，称为全排列， 排列总数为  

 2. 可重复排列

从n个不同元素中每次取出一个， 放回后再取一个，如此连续取 r 次所得的排列称为 可重复排列， 此种排列总数共有   个， 注意， 这里的r允许大于n.

例题： 用 1，2，3，4，5这5个数字可以组成多少个三位数？

解： 组成的三位数是可重复， 属于可重复排列问题，  个数为 5³ = 125.

三. 组合

1. 定义

数学中规定， 0！=1， 

看例题: 有10个球队进行单循环比赛，  问需要安排多少场比赛？

解：  这是从10个球队中任选 2 个进行组合的问题，  选法总数为

 

 即需安排 45 场比赛。

2. 性质
 

，

四   使用组合容易出现的错误

 我们在是否使用组合时， 容易出现一种错误， 即想当然 “用不到组合”

 看一个例子:  一个盒子中有4个白球， 2个黑球， 从盒子任取2个球， 问取到黑球的概率是多少？

这个题目， 有的人一看，  就想当然地认为， 6个中取2个，概率为 ， 这么简单...

我们不禁有疑问， 是这样吗？1/3对吗??   这好像是黑球的组成比例， 不是任取2个球时都是黑球的概率。

实际上，任取2个球的取法有  = 15种，  从盒中取2个黑球的取法有 = 1种 ，概率为， 也就是说，取到2个黑球的概率 远小于1/3,  因为任取的取法是很多的!!! 

五 例题讲解

光说不练是假把式，接下来看几个例题

1 将C，C, E,E, I,N, S 7个字母随机排成一行， 那么恰好排成英文单词 SCIENCE的概率为______.

解析：随机将上述7个字母排成一行的数量为全排列 n=7!,  

按照单词SCIENCE来排列， 要注意不是一种， 不是一种！ 因为C， E是可以调整顺序的。

顺序为  ,

所以 P= 4/ 7! = 1/1260.