离散数学：理解二元谓词逻辑中的量词顺序的蕴含关系

前言

在日常生活中，我们经常使用量词来表达命题，尤其在逻辑学中，量词的顺序对于命题的解释至关重要。

笔者在学习离散数学这门课的过程中，二元谓词逻辑中量词的前后顺序这一主题常常让我感到困惑。每次考试前都是强行背诵下来，考试后就忘记了。

本文将通过一个案例，探讨存在量词和普遍量词在二元谓词中的前后顺序，以及这种顺序如何影响命题的含义，相信看完本文，遇到相关题目都不是问题啦。

---

问题：谓词的三个基本蕴含式

在离散数学的课堂上，老师提到了存在量词和普遍量词在二元谓词中的顺序问题。

刚开始，我对这个概念感到有些摸不着头脑，不知道这究竟是什么意思。尤其是在解题时，我总是容易把顺序搞混，导致对问题的理解产生偏差。

如下图所示，我遇到了下面三个让我困惑的蕴含三兄弟，我曾经思考了好久，到底如何理清楚它们。

今天在复习的时候我想到了一个绝佳的案例用于理解这三个式子，故在此分享出来。

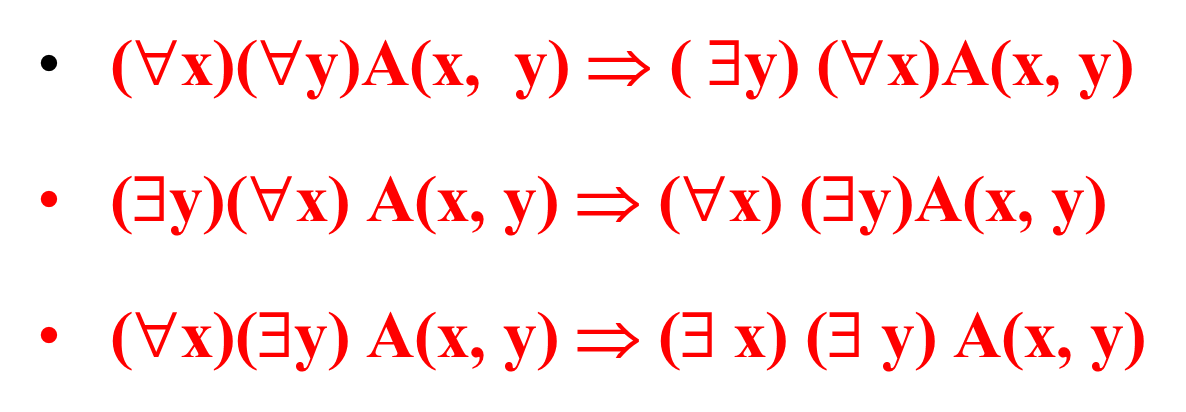
理清概念

第一点，理解谓词的前后顺序

首先，我们理清楚前后顺序分别表示什么，总结下来一句话：顺着读。

在二元谓词中，量词的前后顺序可以影响句子的含义。

这主要涉及到普遍量词（Universal Quantifier）和存在量词（Existential Quantifier）的位置。

1. 存在量词前于普遍量词 (∃x ∀y)：

我们直接顺着读，即这种顺序表示存在一个元素 x，对于所有的元素 y 都满足某个性质。

例如，考虑命题：“存在一个正整数 x，在任何正整数 y 中， x 是 y 的因数”。这可以表示为∃x ∀y。

2. 普遍量词前于存在量词 (∀y ∃x)：

继续顺着读，这种顺序表示对于所有的元素 y，存在一个元素 x 满足某个性质。

例如，考虑命题：“对于任何人 y，存在一本书 x，这本书是 y 所写的”。这可以表示为∀y ∃x。

这两种顺序在语义上有显著的区别，因此在使用量词的时候需要根据具体的语境来确定顺序。

第二点，理解蕴含的定义

在定义上，所谓A蕴含B，即如果A取值为1，那么B一定取值为1，即如果A是真的，那么B一定为真。搞清楚这一点对我们下面案例的理解十分重要。

案例：加深理解

好，现在我们已经知道了量词前后顺序的基本区别，那么回到上面的蕴含三兄弟，我们如何记住他们呢？

这里我举一个小案例，帮助大家记忆蕴含三兄弟。

假设x表示某个人，y表示某种编程语言，A(x，y)表示x擅长y编程语言。为了方便，我们令论域为，x：小红、小明、小李，y：Python、C++、Java。

那么，第一个表达式(∀x)(∀y)A(x, y) 可以翻译为：对于任何一个人，ta都擅长任意一门编程语言。也就是说，小红、小明和小李三人都擅长Java + Cpp + Python。

对于第二个表达式( ∃y) (∀x)A(x, y)可以翻译为：存在一门编程语言，任何人都擅长它。

不妨假设这门语言为C++，那么第一个表达式为真，既然任何人擅长任何语言，那么任何人肯定都擅长C++，因此第一个表达式蕴含第二个表达式，没问题。

对于第三个表达式(∀x) (∃y)A(x, y)，可以翻译为：对于任何一个人，一定存在一门编程语言是ta擅长的。既然任何人都擅长C++，那么对于每个人，肯定至少有一门编程语言是ta擅长的，没问题。

对于第四个表达式(∃x) (∃y)A(x, y)，可以翻译为：存在某个人，ta擅长某门编程语言。这也是可以从第三个表达式推过来的，肯定是成立的。

反推不成立

而反推是不成立的，存在某个人，ta擅长某门编程语言，不一定对于任何一个人，一定存在一门编程语言是ta擅长的，同理知无法反推其余的表达式。

至此，我们就完成了对二元谓词逻辑中的量词顺序的蕴含关系的理解。
希望对大家有所帮助。