这里的数据均来源于吴恩达老师机器学习的课程。
上一篇内容是线性回归,利用线性模型进行回归学习,最终结果是找到一组合适的theta值,使代价函数的值最小,可是对于分类任务该如何解决呢?其实也是希望学习到的也是一组满足这种条件的theta。
先从简单的二分类问题考虑,比如从两门考试的成绩x1,x2,判断录取与否。对于结果y只有两种取值,,录取时y=1,不录取y=0.这时候,如果还像之前那怎样直接相乘算出预测值就不太合适了,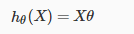
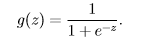
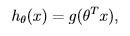
总的来说,方法没有变,只是改了预测函数的形式。
二分类
data = load('ex2data1.txt');
X = data(:, [1, 2]); y = data(:, 3);
figure; hold on;
pos=find(y==1);
neg=find(y==0);
plot(X(pos,1),X(pos,2),'k+','LineWidth',2,'MarkerSize',7);
plot(X(neg,1),X(neg,2),'ko','MarkerFaceColor','y','MarkerSize',7);
% Labels and Legend
xlabel('Exam 1 score')
ylabel('Exam 2 score')
hold off;
[m, n] = size(X);
% Add intercept term to x and X_test
X = [ones(m, 1) X];
% Initialize fitting parameters
initial_theta = zeros(n + 1, 1);
options = optimset('GradObj', 'on', 'MaxIter', 400);
[theta, cost] = fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);
%plot decision boundary
hold on;
if size(X, 2) <= 3
% Only need 2 points to define a line, so choose two endpoints
plot_x = [min(X(:,2))-2, max(X(:,2))+2];
% Calculate the decision boundary line
plot_y = (-1./theta(3)).*(theta(2).*plot_x + theta(1));
plot(plot_x, plot_y)
% Legend, specific for the exercise
legend('Admitted', 'Not admitted', 'Decision Boundary')
axis([30, 100, 30, 100])
else
% Here is the grid range
u = linspace(-1, 1.5, 50);
v = linspace(-1, 1.5, 50);
z = zeros(length(u), length(v));
% Evaluate z = theta*x over the grid
for i = 1:length(u)
for j = 1:length(v)
z(i,j) = mapFeature(u(i), v(j))*theta;
end
end
z = z';
contour(u, v, z, [0, 0], 'LineWidth', 2)
end
hold off;%costFunction.m
function [J, grad] = costFunction(theta, X, y)
m = length(y); % number of training examples
J = 0;
grad = zeros(size(theta));
h=1.0./(1.0+exp(-1*X*theta));
m=size(y,1);
J=((-1*y)'*log(h)-(1-y)'*log(1-h))/m;
for i=1:size(theta,1),
grad(i)=((h-y)'*X(:,i))/m;
end
end
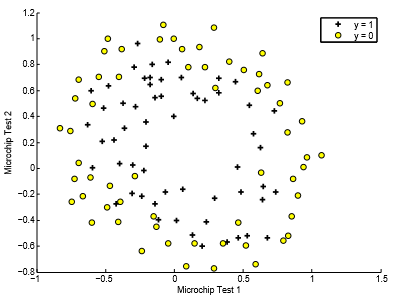
二分类的决策边界不总是直线的,这取决于你的假设函数。例如,当给出的训练数据是这样的:
简单的特征x1,x2,就不能满足了,需要做个映射。
这样就可以很好的分类了。
多分类
二分类问题也可以推广到多分类问题,例如有A,B,C三类,可以训练出三组theta,对于theta1,训练数据的结果只有1-->A,0-->B,C,y预测结果也是[0,1],theta2,theta3,也是如此,最终判断归于是哪一类,就取这三个预测结果更大的那一类。就不累述了。

























 2372
2372

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








