LeetCode刷题-684. 冗余连接

快乐的小小程序猿

已于 2023-09-18 22:41:36 修改

阅读量149

点赞数

分类专栏： LeetCode刷题文章标签： leetcode 算法 Java

于 2023-09-18 22:40:09 首次发布

本文链接：https://blog.csdn.net/xu_benjamin/article/details/133000154

版权

LeetCode刷题专栏收录该内容

302 篇文章

订阅专栏

力扣刷题笔记（六）

684. 冗余连接

难度：中等⭐️⭐️⭐️⭐️

题目

树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

示例 1：

在这里插入图片描述

输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

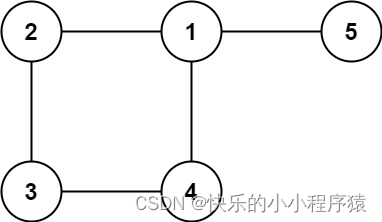
在这里插入图片描述

输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

代码

并查集

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        int[] parent = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            parent[i] = i;
        }
        for (int[] edge : edges) {
            if (find(parent, edge[0]) != find(parent, edge[1])) {
                union(parent, edge[0], edge[1]);
            } else {
                return edge;
            }
        }
        return new int[0];
    }
    private void union(int[] parent, int x, int y) {
        // 把x合并到y所在的集合。x的父节点被改为y的父节点
        parent[find(parent, x)] = parent[find(parent, y)];
    }
    private int find(int[] parent, int x) {
        if (parent[x] != x) {
            // 路径压缩
            parent[x] = find(parent, parent[x]);
        }
        return parent[x];
    }
}

笔记

并查集：可以通过并查集寻找附加的边。初始时，每个节点都属于不同的连通分量。遍历每一条边，判断这条边连接的两个顶点是否属于相同的连通分量。
如果两个顶点属于不同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间不连通，因此当前的边不会导致环出现，合并这两个顶点的连通分量。
如果两个顶点属于相同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间已经连通，因此当前的边导致环出现，为附加的边，将当前的边作为答案返回。
并查集：https://labuladong.github.io/algo/2/20/50/ 、
https://oi-wiki.org/ds/dsu/