DL@数字逻辑@卡诺图及其化简

abtract

• 卡诺图的概念和构造
• 从一般与或式快速得到标准与或式(主范式)

卡诺图

• 用真值表可以描述一个逻辑函数。但是，直接把真值表作为运算工具十分不方便。

• 如果将真值表变换成方格图的形式，按循环码(格雷码)的规则来排列变量的取值组合，所得的真值图称为卡诺图。

卡诺图化简逻辑函数

• 利用卡诺图，可以十分方便地对逻辑函数(变量个数不多的情况下)进行简化，通常称为图解法或卡诺图法。

卡诺图构造

• 将真值表变换成卡诺图，是将变量分成两组。
  • 如果是3变量，则分成AB组，C一组
  • 如果是4变量，则分成AB一组，CD一组。
  • 每一组变量取值组合按循环码的规则排列。
    • 所谓循环码，是相邻两组之间只有一个变量值不同的编码，
    • 例如，2变量的4种取值组合按00-01-11-10排列。

卡诺图中的相邻

• 这里的相邻，包含头、尾两组，即10与00间也是相邻的(同样要求只有一个变量值不同)

变量分组

• 当逻辑函数的变量较多时(超过4个)，每组变量可能含有3个或4个以上的变量。

• 如果是n个变量，则一共有$2^n$个取值组合。

  • 其最低位变量取值按0110重复排列
  • 次低1位按00111100重复排列：
  • 再前1位按0000111111110000重复排列
  • …(参与重复的循环节是对称的;循环节给出的是最长的情况,如果循环节长度达到$2^n$,则不重复)
  • 依次类推，最高位变量的取值是$2^{n-1}$个连0和$2^{n-1}$个连1排列(不对称,不再重复)
  • 这样可以得到$2^n$个取值组合的循环码排列。

附:循环码规律

• 下表给出了2~4个变量循环码的排列，从这个表可以看出循环码排列的规律。

• $2^1$	$2^0$	$2^2$	$2^1$	$2^0$	$2^3$	$2^2$	$2^1$	$2^0$
  A高位	B低位	A高位	B	C低位	A高位	B	C	D低位
  0	0	0	0	0	0	0	0	0
  0	1	0	0	1	0	0	0	1
  1	1	0	1	1	0	0	1	1
  1	0	0	1	0	0	0	1	0
  		1	1	0	0	1	1	0
  		1	1	1	0	1	1	1
  		1	0	1	0	1	0	1
  		1	0	0	0	1	0	0
  					1	1	0	0
  					1	1	0	1
  					1	1	1	1
  					1	1	1	0
  					1	0	1	0
  					1	0	1	1
  					1	0	0	1
  					1	0	0	0

合并规律

（1）2个相邻最小项可合并，并消去1个因子，剩下公共因子；
（2）4个相邻最小项可合并，并消去2个因子，剩下公共因子；
（3）8个相邻最小项可合并，并消去3个因子，剩下公共因子。

合并方法

• 卡诺圈覆盖范围内，某个变量取值有0有1，则该变量可消去

• 剩余变量取值为1的为原变量，取值为0的为反变量

卡诺图合并最小项的特点

1. 任何一个卡诺圈所含的方格数为$2^i$

• 显然不能是奇数

2. 必须按逻辑相邻规则画卡诺圈，包括，
   (a) 相接，即紧挨着的方格相邻；
   (b) 相对，即一行(或一列)的两头、两边、四角相邻；
   © 相重，即以对称轴为中心对折起来重合的位置相邻。
3. $2^m$个方格合并，消去$m$个变量。
   • 合并圈越大，消去的变量数越多。

用卡诺图化简逻辑函数

(1) 把逻辑函数化为最小项表达式；
(2) 画出该逻辑函数的卡诺图；

(3) 画卡诺圈

(4) 写出各卡诺圈对应的与项表达式，并将它们相或。

卡诺圈

指遵循以下规则的卡诺图中的圈：

1. 按 $2^n$大小画方框。(主要项)
2. 使画出的方框的总个数最少，即代数式的与项最少
3. 使每个方框尽可能大，即每个与项的变量最少

卡诺圈之间的要求

1. 每个方框必须有新的含“1”的最小项。(必要项)
2. 用完所有的含“1”的最小项
3. 可以重复使用最小项；

用卡诺图表示逻辑函数的方法

• 由于任意一个n变量的逻辑函数都可以变换成最小项表达式。

• 而n变量的卡诺图包含了n个变量的所有最小项，所以n变量的卡诺图可以表示n变量的任意一个逻辑函数。

• 例如，表示一个3变量的逻辑变量$F(A,B,C)=\sum m(3,5,6,7)$，可以在3变量卡诺图的$m_3,m_5,m_6,m_7$，的小方格中加以标记

  • 一般是在3变量卡诺图对应$m_3,m_5,m_6,m_7$的小方格中填1，其余各小方格填0(或者不填)。
  • 填1的小方格称为1格，填0的小方格称为0格
  • 1格的含义是，当函数的变量取值与该小方格代表的最小项相同时，函数值为1

• 对于一个非标准的逻辑函数表达式（即不是最小项表达式），通常是将逻辑函数变换成最小项表达式再填图。例如

  • $$\begin{array}{rl}F=& AB\bar{C}+\bar{A}BD+AC\\ =& AB\bar{C}\bar{D}+AB\bar{C}D+\bar{A}B\bar{C}D+\bar{A}BCD+\\ & A\bar{B}C\bar{D}+A\bar{B}CD+ABC\bar{D}+ABCD\\ =& \sum m(12,13,5,7,10,11,14,15)\end{array}$$

最小项👺

• 最小项(minterm):一个与项(乘积项)，它包含了某逻辑函数的全部变量，且每个变量在该与项中只出现一次
• 最小项编号：使最小项等于1的一组变量取值组合(二进制)，所转换成对应的十进制数，用$m_i$表示
• 最小项表达式：全部由最小项相加而构成的与-或表达式，又叫标准与-或式、标准积之和式。

直接观察法(与或式)快速绘制卡诺图

• 有些函数变换成最小项表达式时十分繁琐，可以采用直接观察法。
  • 特别是变量多但是逻辑函数与或式中的与项又十分简单,还原标准与或式比较费劲

基本原理

• 在数理逻辑(离散数学)中,我们讨论过任意$n$元逻辑函数F的真值表有$2^n$个不同赋值

• F的标准与或式能够容易得反映(还原)真值表

• F的标准与或式中的与项设有$s$项,那么相应得有$s$个成真赋值,剩余$2^n-s$个都是成假赋值

• 并且如果我们能够枚举(或者已经知道)所有$F$的成真赋值,那么可以立即写出F的标准与或式

• 例如$F$的所有成真赋值为$i_1,\cdots ,i_s$,那么F的标准与火项(最小项间的并)表示为$F=m_{i_1}+\cdots +m_{i_s}$

• 再根据$i_1,\cdots ,i_s$二进制形式对卡诺表填充1即可

• 总结一句话:在逻辑函数与或式F中，与项中只要有一个变量因子(输入变元)的成真赋值取1,该乘积项则为1,从而F成真

• 上述过程和一般的步骤大致相同:先得到标准与或式,再根据各个最小项的成真赋值填充卡诺表

• 重点在于枚举出所有成真赋值

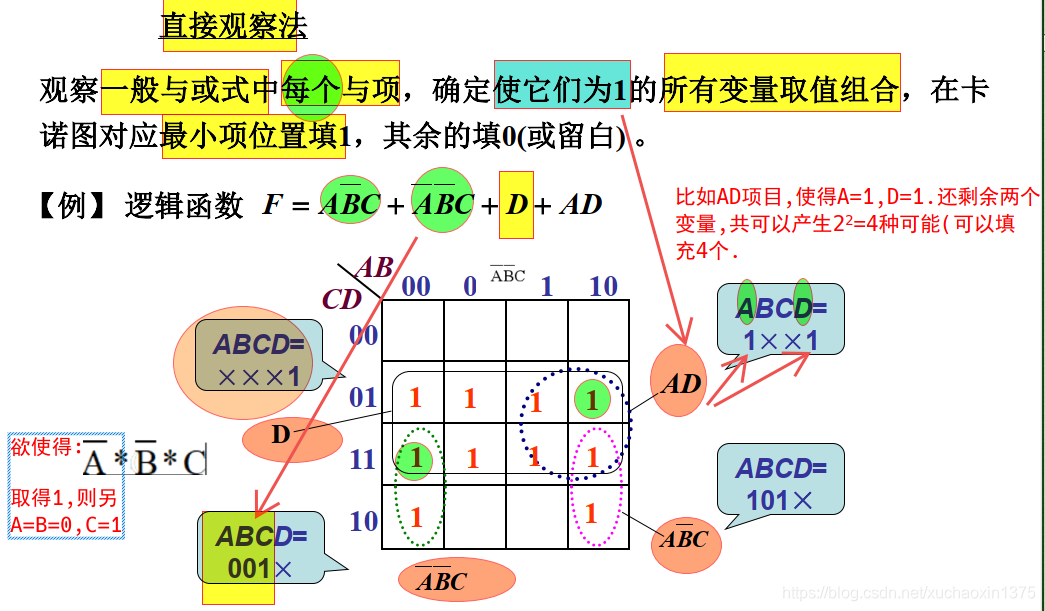
  • 假设4元逻辑函数$F=A\overline{B}C+\overline{A}\overline{B}C+D+AD$

    • 我们分别将上述$F$的4个与项记为$t_1,t_2,t_3,t_4$
    • 则$t_1$相较于4元最小项少了$(D)$,说明$t_1$是$(D)$的无关项
      • (我们不妨用$(D)$表示$D,\overline{D}$中的一个),缺少的这一个文字代表该与或式有1个自由度
      • 设F的输入的4个位为$x_1{x}_2{x}_3{x}_4$,

  • 分别讨论

    1. 令前3位$x_1{x}_2{x}_3$分别取101,那么至少能保证$t_1$此时成真,从而F成真(不论$x_4$取多少不影响F成真)

       1. 1010
       2. 1011

    2. 令赋值的前3位分别为001,则至少能保证$t_2$为1

       1. 0010
       2. 0011

    3. 令$x_4=1$,则能够保证$t_3$成真(前3位有$2^3$中可能取值,它们都能使$t_3$成真)

       1. 0001
       2. 0011(和2.2重复)
       3. 0101
       4. 0111
       5. 1001
       6. 1011(和1.2重复)
       7. 1101
       8. 1111

    4. 令$x_1=1,x_4=1$,则能保证$t_4$成真

       1. 1001(和2.5重复)
       2. 1011(和1.2重复)
       3. 1101(和2.7重复)
       4. 1111(和2.8重复)

  • 根据所有不重复的取值(公10个)填入卡诺表中即可完成卡诺图

改进

• 如果函数能够进行初步化简,应当要先适当化简

• 例如$F=A\overline{B}C+\overline{A}\overline{B}C+D+AD$,

  • $A\overline{B}C+\overline{A}\overline{B}C$=$\overline{B}C(A+\overline{A})$=$\overline{B}C$
  • $D+AD=D$(吸收律)

• 化简成了:$F=\overline{B}C+D$

$w_1=\overline{B}C$	$w_2=D$	备注
1.0010 2.0011 3.1010 4.1011	1. 0001 2. 0011(重复) 3. 0101 4. 0111 5. 1001 6. 1011(重复) 7. 1101 8. 1111	$w_1,w_2$中仍然有重复,但是容易去除 只要将$w_1$中最后一位是1再合计时剔除即可
x01x	xxx1

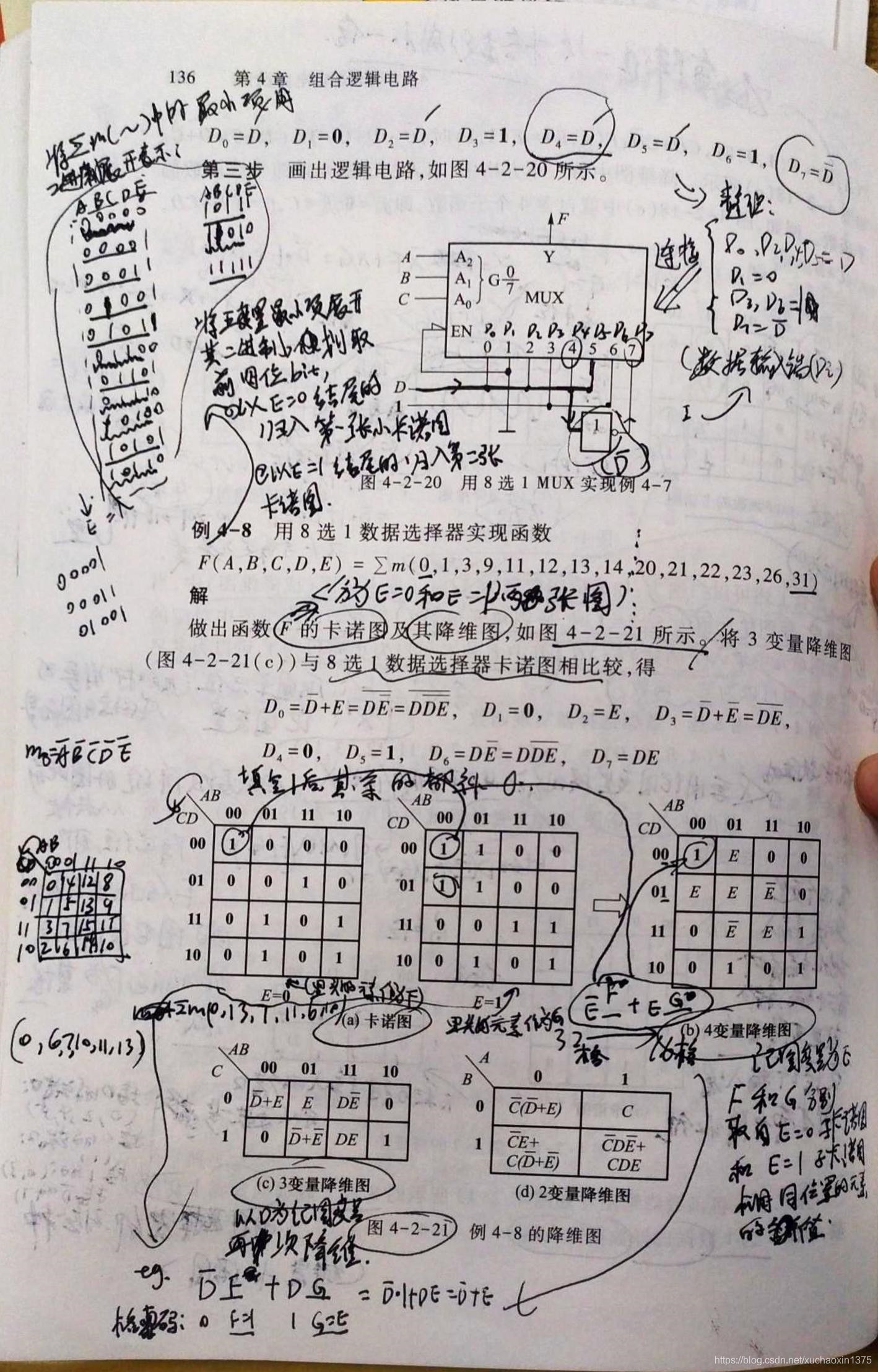
5变量卡诺图